Evolución del área de contacto con carga normal para superficies rugosas:de escalas atómicas a macroscópicas

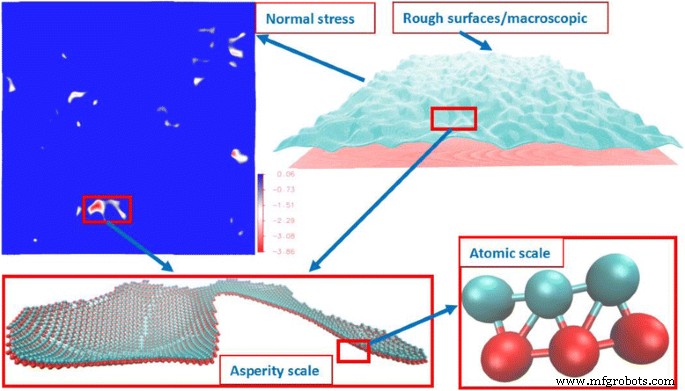
El modelo GFMD a diferentes escalas, desde la escala atómica hasta la escala macroscópica (en σ )

Además, la superficie total de cumbre / valle número N es expresado por

donde A ₀ es la superficie aparente. Para la superficie fractal auto-afín, los parámetros estadísticos de la superficie están relacionados con los parámetros de entrada ( w , H , P ) por la siguiente ecuación:

donde B es la constante de rugosidad de la superficie, que está relacionada con P . Las ecuaciones (3) y (2) indican que el número de cumbre / valle de la superficie fractal depende de la longitud de onda y del exponente de Hurst. Se pueden encontrar discusiones detalladas sobre las propiedades estadísticas de la superficie fractal en la literatura [25, 26].

En el algoritmo de transformada de Fourier, como ejemplo típico, configuramos el componente de Hurst en H =0.5, la frecuencia máxima debe ser w _L =1 / (24 σ ), la frecuencia mínima debe ser w _H =1 / (256 σ ), la desviación estándar de la amplitud de frecuencia debe ser P =0,69, y el tamaño del sistema será de 512 × 512 átomos (con un espaciado inicial igual a 1,12 σ ). Estos parámetros de entrada generan posteriormente la superficie con los siguientes parámetros estadísticos:pendiente RMS de superficie \ (\ sqrt {M_2} =0.077 \) y curvatura RMS \ (\ sqrt {M_4} =0.0077 \) . El número total de cumbres / valles superficiales es 150 según la ecuación. (2), mientras que al contar el número numéricamente, el número de la cumbre de la superficie es 158 y el número del valle es 159. El error está dentro del 5%, lo que sugiere que el tamaño del sistema es aceptable en un sentido estadístico. De hecho, cuando aumentamos el tamaño del sistema hasta 2048 × 2048 átomos (con un espaciado inicial igual a 1,12 σ ), los resultados de los parámetros estadísticos son coherentes con los del sistema más pequeño.

Modelo GFMD

La interacción entre partículas es muy difícil de capturar experimentalmente [6, 27]. Recientemente, se ha utilizado la dinámica molecular para simular la interacción entre partículas, con el objetivo de investigar los orígenes moleculares del mecanismo de contacto / fricción. Sin embargo, el gasto computacional es considerablemente alto para las simulaciones de dinámica molecular a gran escala. Por tanto, se introduce GFMD para simular la superficie debido a su alta eficiencia. GFMD usa dinámica molecular para simular la interacción de los átomos de la interfaz (dos capas aquí), mientras que la capa sin interfaz, que generalmente exhibe comportamientos elásticos, es simulada por la función de Green. Por lo tanto, reduce el gran sistema atómico a átomos de dos capas en la interfaz (como se ve en la Fig. 1), lo que reduce drásticamente el gasto computacional. En la literatura se pueden ver discusiones detalladas sobre la DMG [21, 22, 23, 28]. En el modelo GFMD, el potencial de Lennard-Jones (LJ) se utiliza para simular la interacción entre partículas. La ecuación se escribe como

donde ε es la profundidad del pozo potencial, σ es la distancia finita a la que el potencial entre partículas es cero, y r es la distancia entre las partículas. Tomamos ε , σ y ε / σ como energía, unidad de distancia y unidad de fuerza, respectivamente. Según el potencial de LJ, sabemos que cuando r =2 ^1/6 σ ≈ 1,12 σ , la fuerza entre partículas es cero. Cuando r > 1,12 σ , la fuerza entre partículas es atractiva; cuando r <1,12 σ , la fuerza entre partículas es repulsiva. Dado que no consideramos la adhesión en este trabajo, la distancia de corte se establece en 1.12 σ . La estructura cristalina utilizada para la capa atómica es cúbica centrada en la cara (FCC). Debido a la simetría, solo tomamos la capa de la interfaz para formar la geometría de la superficie como se muestra en la Fig. 1, y el bloque elástico debajo de la superficie plana es simulado por la función de Green.

Método de reconocimiento de clúster de contacto

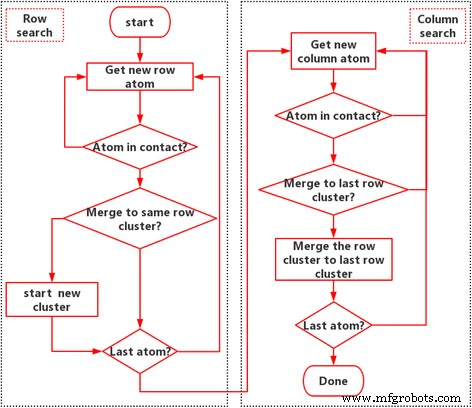
Hay tres escalas observadas en la interfaz como se ve en la Fig. 1:(1) escala atómica, que es simulada por el potencial LJ; (2) escala de aspereza, que es el efecto de grupo de los átomos de contacto; y (3) escala macroscópica, que es el efecto de grupo de los grupos de contactos. El tamaño, la forma, la ubicación y la distribución de los grupos de contactos son el puente crítico entre el comportamiento molecular y las propiedades de la interfaz. A nanoescala, la región de contacto atómico es difícil de definir [6]. Aquí definimos un átomo de contacto por su componente normal de fuerza fz> 0. Posteriormente, los átomos en contacto conectados se definen como un grupo en contacto. La técnica de etiquetado [29, 30] se utiliza para buscar el grupo de contactos. Aquí, utilizamos un algoritmo modificado para la aceleración, que evita el proceso de búsqueda recursiva. El diagrama de flujo del algoritmo se muestra en la Fig. 2, donde los datos de la fuerza atómica se extraen de la función de simulación de dinámica molecular de Green. El algoritmo se divide en ocho pasos clave de la siguiente manera.

Algoritmo de detección de clústeres de contactos:la técnica de etiquetado

Paso 1. Inicie la búsqueda de filas y obtenga los datos del nuevo átomo, es decir, busque los átomos de fila a fila.

Paso 2. Determine si el átomo está en contacto. Si no está en contacto, regrese al paso 1. Si está en contacto, continúe con el siguiente paso.

Paso 3. Compare el átomo actual con el átomo anterior en la misma fila. Si el átomo anterior también está en contacto, fusiona el átomo en el grupo al que pertenece el átomo anterior, luego etiqueta el átomo con el mismo número que el átomo anterior. Si el átomo anterior no está en contacto, rotule el átomo con un nuevo número que sea el número anterior más uno.

Paso 4. Determine si es el último átomo; si no es así, vuelva al paso 1 o vaya al proceso de búsqueda de columnas.

Paso 5. Inicie la búsqueda de columnas y obtenga los datos del nuevo átomo, es decir, busque los átomos de una columna a otra.

Paso 6. Determine si el átomo está en contacto. Si no está en contacto, regrese al paso 5. Si está en contacto, continúe con el siguiente paso.

Paso 7. Compare el átomo actual con el átomo anterior en la misma columna. Si el átomo anterior también está en contacto y pertenece a un grupo diferente, fusionar el grupo actual en el grupo al que pertenece el átomo anterior, luego etiquetar los átomos con el mismo número y almacenarlos. Si el átomo anterior no está en contacto o pertenece al mismo grupo, continúe con el siguiente paso.

Paso 8. Determine si el átomo actual es el último átomo; si no es así, vuelva al paso 5 o el proceso de búsqueda habrá finalizado.

Diseño experimental numérico

Es bien sabido que el problema de contacto de dos superficies rugosas se puede simplificar como un problema con una superficie rugosa rígida compuesta y una superficie elástica plana introduciendo el módulo de elasticidad equivalente E * , que está escrito como

$$ \ frac {1} {E ^ {\ ast}} =\ frac {1- {v} _1 ^ 2} {E_1} + \ frac {1- {v} _2 ^ 2} {E_2} $$ ( 5)

donde E ₁ y E ₂ son el módulo elástico de la superficie superior y la superficie inferior, respectivamente. Para simplificar, consideramos una superficie rugosa rígida en contacto con una superficie lisa elástica y luego estudiamos la formación y desarrollo del grupo de contacto y su comportamiento fuerza-área. En la siguiente discusión, usaremos la superficie generada arriba (la superficie superior es rígida y rugosa ( E ₁ =∞), y la superficie inferior es lisa y elástica ( E ₂ =3 ε / σ ³ )) para estudiar el comportamiento de contacto, donde ambos v ₁ y v ₂ se establecen en 0,5. El tamaño de nuestro sistema es de 512 × 512 átomos (con un espaciado inicial igual a 1,12 σ ), y las condiciones de contorno periódicas se utilizan en el x - y avión. La profundidad del bloque elástico se establece en 1024 capas atómicas (con un espaciado inicial igual a 1.12 σ ). En una simulación de dinámica molecular regular, el sistema estará compuesto por 268 697 600 átomos; el modelo GFMD reduce el número a 524,288 (dos capas de átomos), como se ve en la Fig. 1. Empujamos gradualmente la superficie rugosa (en la parte superior) hacia la superficie plana elástica. La carga de la superficie rígida está controlada por el desplazamiento. Cada paso de carga de desplazamiento se establece en 0.01 σ , y el algoritmo GFMD actualizará la posición de cada átomo hasta que la fuerza atómica cumpla con los criterios de convergencia L ¹ -norm =0.01 ε / σ. El número máximo de iteraciones se establece en 50.000 para evitar un bucle sin fin.

Resultados y discusión

Cómo ponerse en contacto con la distribución y el desarrollo de los clústeres

El modelo de aspereza considera que la aspereza es esférica o elíptica y no considera la interacción entre las asperezas en contacto. En este trabajo, las asperezas utilizadas en el modelo de aspereza se extraen de la superficie generada arriba. En el modelo de aspereza, las asperezas potenciales en contacto pueden determinarse por adelantado mediante la geometría de la superficie en función de sus alturas; es decir, las cumbres / valles de la superficie se formarán como grupos de contacto de acuerdo con sus alturas. Sin embargo, en realidad, la aspereza tiene una forma irregular y, por lo general, varias asperezas adyacentes pueden fusionarse en una grande, como se muestra en la Fig. 2. Se observa que hay seis asperezas independientes al principio, y como fuerza de contacto aumenta, finalmente se fusionan en un gran grupo de contactos (Fig. 3). Esto sugiere que la suposición de que la distancia entre asperezas es lo suficientemente grande para que las asperezas no se afecten entre sí puede conducir a resultados inexactos.

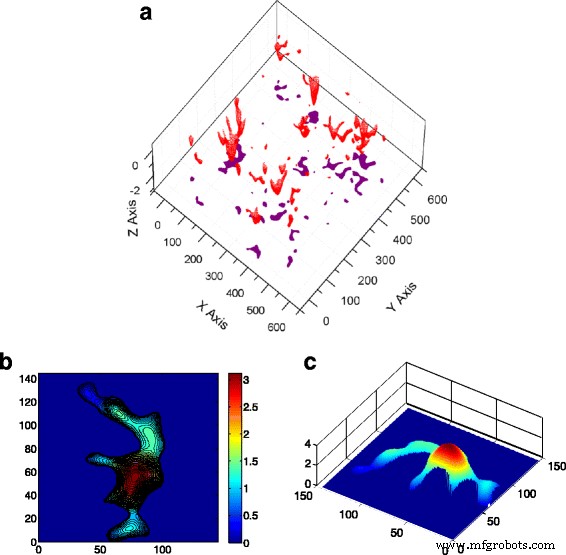
La forma de los racimos y el efecto de fusión. un La vista 3D de los grupos de contactos y su proyección en la x - y plano (en σ ). b Un grupo de contactos típico que comprende seis asperezas independientes. c La vista 3D de la geometría del grupo de contactos (en σ )

La Figura 4 demuestra que el número de conglomerados primero aumenta y luego disminuye a medida que aumenta el área de contacto, mientras que la aspereza de la superficie siempre aumenta a medida que aumenta el área de contacto. Esto se debe al efecto de fusión explicado en la Fig. 3.

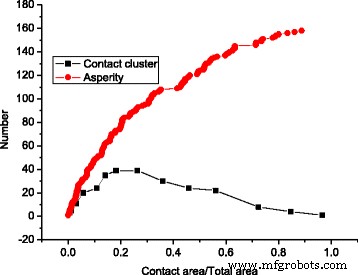
Valles de superficie y número de conglomerados bajo diferentes áreas de contacto

El efecto de fusión del grupo de contactos se ha observado tanto en el modelo de aspereza como en el modelo GFMD. Sin embargo, con la misma área de contacto, el número de grupos de contactos en el modelo GFMD es mucho mayor que el del modelo de aspereza, como se ve en la Fig.5. Se observa que el número de grupos de contactos en el modelo GFMD es casi el doble que en el modelo de aspereza, como se muestra en la Fig. 5. La principal razón de esto es que el modelo de aspereza no considera la interacción entre asperezas. Sin embargo, en el modelo GFMD, los grupos de contactos se influyen entre sí. Los campos de desplazamiento generados por los grupos de contactos son continuos en toda la superficie. El desplazamiento del gran conjunto de grupos da como resultado una nueva geometría en la superficie elástica, lo que afecta la formación de nuevos grupos de contactos. Por lo tanto, la formación del grupo de contactos no solo se basa en la altura de la superficie rugosa rígida, sino que también puede verse influenciada por deformaciones en la superficie elástica lisa. Esto también se puede observar en la Fig. 6, que muestra la distribución del grupo de contactos en diferentes áreas para el modelo de aspereza y el modelo GFMD, respectivamente. Como se muestra en la Fig.6, en un área de contacto del 5%, los números de grupo de contactos son 17 y 34 para el modelo de aspereza y el modelo GFMD, respectivamente, mientras que en un área de contacto del 10%, sus números de grupo de contactos se vuelven 24 y 52 , respectivamente. Esto sugiere que los grupos de contactos en el modelo GFMD son más discretos que los del modelo de aspereza. En el modelo GFMD, el tamaño promedio de los conglomerados es menor, pero la mayoría de los conglomerados coincidirán con las cumbres / valles, como se puede observar en la Fig. 7. Además, el modelo de aspereza considera los valles o las cumbres como posibles asperezas ( dependiendo de qué lado esté en contacto). Sin embargo, en la Fig. 8, encontramos que a medida que aumenta el área de contacto, tanto las cumbres como los valles pueden estar en contacto. En la Fig. 8, la mayoría de las asperezas en contacto son los valles de la superficie cuando el área de contacto es pequeña. Sin embargo, cuando el área de contacto es mayor al 10% de la superficie, también se pueden formar más y más cumbres como grupos de contacto.

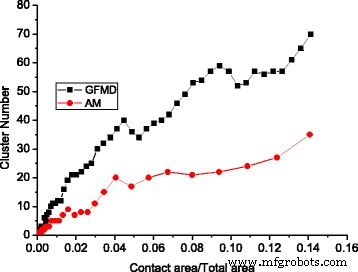
El desarrollo de clústeres para diferentes modelos

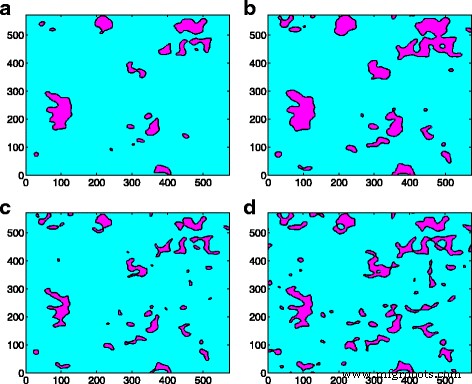
El contorno de distribución de conglomerados (en σ ) en diferentes áreas de contacto para el modelo de aspereza y el modelo GFMD, respectivamente. un Modelo de aspereza con 5% de área de contacto. b Modelo de aspereza con un 10% de área de contacto. c Modelo GFMD con 5% de área de contacto. d Modelo GFMD con un 10% de área de contacto

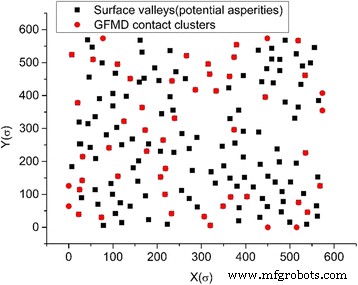
Las ubicaciones de los grupos de contacto y los valles de la superficie al 10% del área de contacto

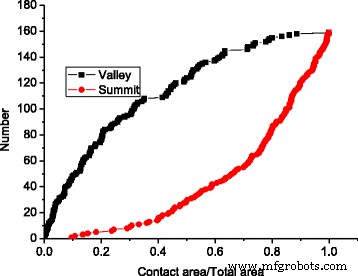
El número de cumbres y valles de la superficie crece en diferentes áreas

Relación entre área de contacto y carga

La relación fuerza-área bajo una carga normal es esencial para el comportamiento del contacto. En los modelos anteriores, las asperezas generalmente se consideran esféricas y elípticas. Sin embargo, los clústeres de contactos reales son mucho más complicados. En esta sección, comparamos la relación fuerza-área de contacto de tres modelos:(1) el modelo GFMD; (2) el modelo de aspereza (marcado como AM), en el que la aspereza se extrae directamente de la superficie antes de usar GFMD para empujar esas asperezas hacia la superficie elástica plana (esto asegura que no haya una formación inesperada de grupos de contacto durante el contacto); y (3) el modelo de Greenwood y Williamson (marcado como G-W), en el que la aspereza se convierte en la esfera equivalente. El radio de la esfera se obtiene mediante

$$ \ frac {1} {R} =\ frac {8} {3} {\ left (\ frac {m_4} {\ pi} \ right)} ^ {1/2} $$ (6)

Para el modelo GFMD y el modelo de aspereza con asperezas extraídas exactamente de la superficie, las fuerzas totales en la interfaz se pueden obtener sumando las fuerzas de cada grupo de contacto extraídas de GFMD. Para el modelo de Greenwood y Williamson, usamos la teoría de Hertz para cada fuerza de aspereza (con la misma propiedad material usada en el modelo GFMD), lo que significa que la fuerza total F se puede expresar como

$$ F =\ suma \ límites_ {i =1} ^ n {f} _i =\ suma \ límites_ {i =1} ^ {\ mathrm {N}} \ frac {4} {3} {E} ^ { \ ast} {R} ^ {1/2} {\ left (d- {z} _i \ right)} ^ {3/2} $$ (7)

donde Z _i es la altura de la aspereza, d es el desplazamiento aplicado en la superficie rígida, y f es la fuerza de contacto de aspereza basada en la teoría de contacto de Hertz.

En la figura 9, comparamos las relaciones fuerza-área de los tres modelos, que exhiben relaciones lineales. Se observa que la fuerza total en GFMD es mucho menor que la del modelo de aspereza y el modelo G-W. F en el modelo de aspereza es 1,80 veces mayor que el predicho por GFMD, y F en el modelo G-W es 1,54 veces mayor que el predicho por GFMD. Esto puede explicarse por la pendiente RMS de los grupos de contactos. Se sabe que la carga normal es proporcional a la pendiente RMS, es decir, \ (L \ propto \ sqrt {M_2} \). En el modelo GFMD, el área de contacto está compuesta por un mayor número de conglomerados, cuyas penetraciones son menores que las del modelo de aspereza. Dado que la pendiente de la punta de aspereza es menor, la pendiente RMS para el grupo de contactos en el modelo GFMD también es menor. La Figura 10 muestra las pendientes RMS del grupo de contactos para los tres modelos. Se puede ver que la pendiente RMS de los clústeres de contacto en GFMD es menor que la pendiente RMS superficial de 0.077, mientras que las pendientes RMS del clúster de contacto de los otros dos modelos son más grandes que la pendiente RMS superficial.

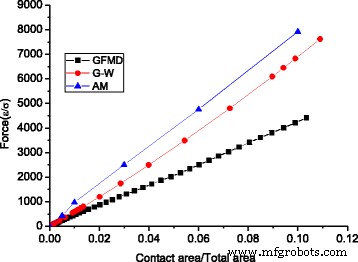
Relación del área de contacto y carga para diferentes modelos

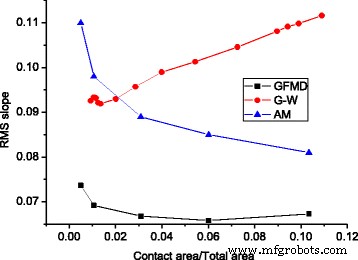
Pendiente RMS de los grupos de contactos con diferentes áreas de contacto para diferentes modelos, donde la pendiente RMS de la superficie es 0.077

Conclusiones

Para encontrar la evolución del área de contacto desde la escala atómica a la escala macroscópica, se ha estudiado el problema del contacto superficial fractal rugoso utilizando el modelo GFMD. Definimos el contacto atómico por la existencia de una fuerza mayor que cero y estudiamos tres escalas de longitud diferentes en el mismo sistema. Se encuentra que la interacción entre asperezas es esencial para la formación de un grupo de contactos. Algunos grupos están lo suficientemente cerca como para fusionarse en uno grande. La región de contacto real es mucho más complicada que la predicha por la geometría de la superficie debido a la deformación elástica en la superficie lisa elástica. La mayoría de las ubicaciones de los grupos de contactos coinciden con las cumbres / valles de la superficie. Sin embargo, el tamaño del cúmulo es más pequeño y su formación no está determinada por las alturas de aspereza de la superficie. A medida que aumenta el área de contacto, tanto las cumbres como los valles pueden formarse como grupos de contacto. En el modelo GFMD, la fuerza es mucho menor que la del modelo de aspereza, mientras que el número de grupo de contactos en el modelo GFMD es mucho mayor. La pendiente RMS de los grupos de contactos en el modelo GFMD es más pequeña que la del modelo de aspereza, lo que explica por qué el modelo de aspereza conduce a una presión más alta. Nuestros hallazgos sugieren que el área de contacto real no se puede predecir simplemente por la geometría de la superficie. El área de contacto real con la carga normal es de importancia para la siguiente investigación sobre la fricción.

Matrices de nanotubos de TiO2:fabricadas con una plantilla blanda-dura y la dependencia del tamaño de grano del rendimiento de las emisiones de campo Capas óptimas de dopaje de silicio de barreras cuánticas en la secuencia de crecimiento que forman el potencial de confinamiento suave de ocho períodos In0.2Ga0.8N / GaN Pozos cuánticos de azul LE…