Síntesis de compuesto de nanopartículas de oro / nanofibras de sílice conductoras eléctricas mediante pulsos de láser y técnica de pulverización

Antecedentes

Los materiales de detección biocompatibles tienden a ser costosos de producir, además de tener una baja relación señal / ruido (SNR); Una relación señal / ruido es una medida de la potencia de la señal a un nivel de potencia de ruido (ruido de fondo) y se expresa como una medida de decibelios (dB). Los nanomateriales se introdujeron como un intento de reducir la amortiguación causada por el ruido. Se utilizan dos métodos principales para reducir la amortiguación, a saber, la formación de nanotubos de carbono y los nanomateriales [1]. El éxito de los nanotubos de carbono como sensores puede atribuirse a su mayor área de superficie efectiva, que disminuye la impedancia del electrodo y aumenta la corriente [1-4]. El aumento de la superficie también inmoviliza más enzimas en aplicaciones biomédicas [2]. Sin embargo, existen algunas desventajas en la fabricación de nanotubos de carbono. Por ejemplo, es caro y tiene baja pureza, falta de control de alineación, falta de solubilidad acuosa y alta reactividad causada por nanotubos colgantes [5].

Las reacciones tisulares adversas y la resistencia a la degradación son factores de biocompatibilidad importantes [6]. El silicio poroso, que está formado por una estructura única de nanocristalitos y poros, exhibe propiedades que son valiosas para su uso como biomaterial y posibles aplicaciones de biosensores [7]. El silicio, un material de uso común, es versátil en las técnicas de microprocesamiento contemporáneas debido a su disponibilidad y bajo costo [8, 9]. El silicio se puede procesar para formar macro, micro y nanoporos. El diámetro de poro ideal para dispositivos de detección biocompatibles está entre 2 y 50 nm. Estos tamaños de poros permiten una difusión biomolecular y una mayor exposición de la superficie, lo que resulta en una mayor inmovilización de biomoléculas en comparación con las superficies 2D y lo convierte en un material excelente para aplicaciones de biosensores [8].

Se pueden usar varios métodos para modificar la superficie de los sustratos de silicio para fabricar sensores basados ​​en silicio. El grabado electroquímico se utiliza en muchos casos para modificar el silicio en una estructura porosa. Este método requiere el uso de varios productos químicos y equipos especializados. El procedimiento inicialmente requiere una limpieza a fondo de la oblea. Ciertos productos químicos pueden reaccionar en gran medida a los defectos en la estructura del silicio y liberar gases tóxicos [9, 10]. El grabado electroquímico también influye fuertemente en la topografía de la superficie, lo que dificulta su control [11]. Lograr una superficie porosa uniforme utilizando esta técnica es complejo y altamente dependiente y sensible a los parámetros de grabado, lo que también resulta en la producción de grandes cantidades de desechos [12]. Además, una alta concentración de enlaces de hidrógeno cede en la superficie del poste de preparación, haciéndola muy inestable [8]. La fotolitografía es otro método para modificar la superficie de los sustratos de silicio con el fin de fabricar un sensor biocompatible a base de silicio [13, 14]. Este método permite la creación de patrones y el control del comportamiento celular. Su principal desventaja es que debido a la difracción óptica del haz de luz, la resolución está limitada a un máximo de 1 μ en la práctica.

El procesamiento con láser es otro método para modificar la superficie de los sustratos de silicio. Se utiliza para optimizar el rendimiento de un material, como su absorción, susceptibilidad al desgaste, química de la superficie y estructura cristalina. Las propiedades de la superficie se pueden controlar de esta manera sin afectar la mayor parte del material [8, 9].

La adición de nanopartículas de oro es un método atractivo para modificar la superficie de los sustratos de silicio con el fin de fabricar un sensor de silicio. Las nanopartículas de oro tienen propiedades importantes que incluyen su conductividad, alta relación superficie-volumen, excelente reconocimiento molecular y alta energía superficial [15, 16]. Sus propiedades químicas y físicas únicas ayudan a transferir electrones desde la capa bioespecífica a la superficie del electrodo [15]. Las nanopartículas de oro también aumentan la sensibilidad de la detección bioquímica de biosensores electroquímicos [17, 18].

Los resultados publicados anteriormente por Colpitts y Kiani han demostrado el uso de un sistema de láser pulsado de nanosegundos en la formación de estructuras fibrosas biocompatibles en silicio [12, 19]. Sus resultados iniciales inspiraron el objetivo de esta investigación de proponer un método para personalizar las propiedades del silicio procesado con láser para mejorar su viabilidad en futuras aplicaciones de detección biológica que requieran propiedades tanto de biocompatibilidad como de conductividad eléctrica. También se describe un método eficaz para generar óxido de silicio nanofibroso utilizando un láser pulsado de nanosegundos comercial. Esto implicó el procesamiento de una oblea de silicio cristalino utilizando un láser pulsado de nanosegundos Nd:YAG a una potencia constante de 12 W con una variación en las superposiciones (número de escaneo del rayo láser a través de la misma ruta) y espaciamientos de línea (distancia entre rutas de escaneo) . A continuación, se llevó a cabo una pulverización catódica de oro sobre su superficie durante 4 u 8 minutos. Se investigaron y discutieron los cambios en la absorción y conductividad, así como en la topografía de la superficie.

Materiales y métodos

Este enfoque implicó el procesamiento con láser de una oblea de silicio monocristalino <100> a una potencia promedio de 12 W, con espaciamientos de línea de 0.025, 0.1 y 0.15 mm, y en uno, tres o cinco solapamientos. El espaciado de línea se refiere al espacio entre cada línea sucesiva pulsada por el láser, midiendo desde el centro del rayo láser. Las superposiciones (OL) denotan el número de repeticiones de patrones realizadas en la superficie del silicio, por ejemplo, tres superposiciones significarían que el rayo láser pasa sobre la línea ablacionada tres veces. Estos se pulverizaron con oro durante 4 u 8 minutos. La figura 1 ilustra el proceso general.

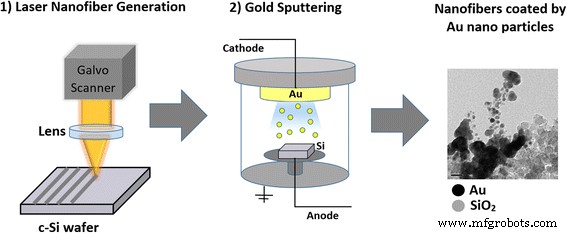
Enfoque I:pulverización catódica de oro de nanofibras de óxido de silicio generadas por láser

Procesamiento láser

Para este experimento se utilizó un láser pulsado de nanosegundos Nd:YAG con una longitud de onda de 1064 nm. El haz de salida circular del láser tiene un diámetro de 9 mm y se reduce a 8 mm utilizando un diafragma de iris antes de entrar en un escáner de galvanómetro XY (JD2204 de Sino-Galvo). Este escáner tiene una apertura de 10 mm y un desplazamiento del haz de 13,4 mm. Se utilizó una lente F-theta con una distancia focal de 63,5 mm para controlar el enfoque del láser en la superficie de la muestra, lo que resultó en un diámetro teórico del punto láser de 20 μm. El software EZCAD se utilizó para controlar los parámetros del láser, por ejemplo, para especificar velocidades de escaneo, superposiciones, frecuencia y patrones de líneas.

Microscopía y caracterización de superficies:microscopio electrónico de barrido (SEM) y microscopio electrónico de transmisión de barrido (TEM) y rayos X de dispersión de energía (EDS)

Se emplearon diversos medios para la caracterización de la superficie, incluido un microscopio electrónico de barrido (SEM) JEOL JSM-6400 montado con un sistema de rayos X de dispersión de energía (EDS) EDAX Genesis 4000 y un microscopio electrónico de transmisión de barrido (TEM) JEOL JEM-2010 adaptado con una cámara Gatan UltraScan usando DigitalMicrograph para recolectar las imágenes deseadas.

Espectroscopia de luz

Se utilizó el espectroradiómetro STS-NIR (Ocean Optics, Dunedin, Florida, EE. UU.) Para determinar las propiedades ópticas de las muestras, es decir, para medir el coeficiente de reflectividad de las muestras en diferentes superposiciones y espaciamiento de líneas en longitudes de onda entre 175 y 885 nm. y una resolución óptica de 1,5 nm [19].

Espectroscopia de impedancia

Se usó un potenciostato modelo 760 de CH Instruments Inc. (EE. UU.) Para medir la conductividad de las muestras de silicio procesadas usando espectroscopía de impedancia CA. Las muestras se conectaron mediante pinzas de cocodrilo al espectrómetro (modo de dos electrodos) y las mediciones se obtuvieron a frecuencias entre 0 y 1 × 10 ⁶ Hz y con una amplitud potencial de 10 mV.

Análisis de imagen

El software ImageJ 1.501 de Wayne Rasband en los Institutos Nacionales de Salud, EE. UU., Se utiliza para determinar los diámetros de partículas y fibras. Permite la importación y medición manual de las características capturadas por imágenes SEM y TEM.

Resultados y discusión

Generación de estructuras nanofibrosas

Las muestras de silicio se procesaron en uno, tres y cinco solapamientos a una potencia promedio de 12 W con espaciamientos de línea de 0.025, 0.10 y 0.15 mm. Se recolectaron imágenes SEM para determinar el tipo de nanoestructuras presentes.

El aumento del espaciado de líneas dio como resultado la formación de micropartículas con porosidad a nanoescala en lugar de nanofibras. El área sometida a ablación con láser es claramente evidente tanto en (a) como en (b) de la figura 2, como se esperaba, ya que el diámetro del punto de láser es de aproximadamente 0,02 mm y mucho más pequeño que el espaciado de línea designado. A 0,1 mm, se forman micropartículas en la superficie entre las regiones sometidas a ablación con láser. Un aumento mayor revela que estas micropartículas están formadas por estructuras fibrosas finas. A 0,15 mm, las micropartículas son más pequeñas y más dispersas, con una mayor densidad de nanopartículas que se forman en la superficie. La porosidad de las nanoestructuras difiere de las micropartículas más grandes. Las micropartículas con un espaciado de línea de 0,15 mm tienen una estructura más densa en comparación con la muestra de 0,1 mm. En teoría, se espera que un aumento en la temperatura de la pluma de plasma láser resulte en el crecimiento de partículas [20], como se puede observar al comparar las imágenes en la Fig. 2.

Imágenes SEM de silicio procesado con láser en cinco superposiciones (OL) con interlineado de a 0,1 mm, b 0,15 mm

Las imágenes SEM en la Fig. 3 muestran (a) una dispersión uniforme de nanofibras entrelazadas que se forman con un espaciado de línea de 0.025 mm. Cuando el número de superposición aumenta a tres, (b) comienzan a formarse pequeños grupos de partículas nanofibrosas. En la quinta superposición, (c) se forman grupos claros de estructuras nanofibrosas con espacios entre ellos. Nuevamente, se espera que el aumento de la superposición aumente el crecimiento de partículas debido al aumento de temperatura y absorción de luz. También se observó un aumento en el diámetro de la fibra con superposiciones crecientes. Sobre la base de imágenes SEM, los diámetros de las fibras se analizaron utilizando un software de visualización de imágenes ImageJ 1.501 desarrollado por Wayne Rasband en los Institutos Nacionales de Salud de EE. UU. El diámetro de fibra más pequeño, un promedio de 75 nm, se observó en un solapamiento. La literatura indica que las estructuras nanoporosas aumentan la biocompatibilidad del material al afectar la topología y el andamiaje celular [21].

Imágenes SEM de silicio procesado con láser con un espaciado de línea de 0,025 mm. Desde la izquierda a la derecha , la superposición cambia de uno, tres y cinco, respectivamente (el npannel dentro de cada imagen muestra una imagen SEM de gran aumento)

No es sorprendente que se haya observado una generación óptima de nanofibras con el espaciado de línea más pequeño de 0,025 mm. Dado que el diámetro del láser es teóricamente muy cercano al tamaño de este espaciado de línea, queda poca o ninguna área que no entre en contacto directo con el láser. Esto da como resultado una región más caliente y la densidad de la pluma se mantiene estable durante un período más largo. Esto aumenta aún más la absorción total de luz de la muestra debido al cambio de topografía. Al crear una red de fibra, la superficie aumenta y por tanto se potencian todos los mecanismos directamente vinculados a la zona.

La eliminación de material de una superficie sólida mediante la tecnología de láser pulsado puede inducir la formación de nanopartículas. Cuando el láser se ilumina sobre una superficie, induce la vaporización y elimina los átomos de la superficie a granel, lo que permite que el pulso del láser penetre más profundamente en el material. La profundidad del láser depende de factores como su longitud de onda y las propiedades físicas del material. Los campos electromagnéticos del láser expulsan electrones al descargar energía e impulso en la superficie del material. La transferencia de energía involucrada en la interacción del láser con el material hace que su temperatura aumente, lo que a su vez provoca la formación de un gas ionizado conocido como plasma que se expandirá como una onda de choque alrededor del foco del láser. Las partículas se eliminan de la superficie cuando la intensidad del láser (fluencia) es mayor que el umbral de ablación del material. El contenido del plasma toma la forma de una pluma:una región que contiene una mezcla de iones, electrones y nanopartículas que son altamente reactivas. Cuando la ablación con láser se realiza en el aire, puede producirse la oxidación de las partículas expulsadas. A medida que la pluma se expande, sus extremidades son más frías que su núcleo [22]. Como resultado, las partículas recién formadas se mueven hacia regiones más frías, lo que hace que se sobresaturan, se nucleen más y se cristalicen en una estructura sólida. Las colisiones entre los átomos de gas y la pluma ablacionada en la capa de interfaz delgada generan nanopartículas y agregados. El gas ambiental se fusiona con los átomos e iones evaporados a altas temperaturas. A medida que la pluma se enfría, comienza la formación de agregados. Al final del pulso láser, se producen uniones agregado-agregado y átomo-agregado [23].

Los coeficientes de absorción de luz se determinaron experimentalmente mediante espectroscopía de luz. Como muestra la Fig. 4, las distancias entre líneas más estrechas dieron como resultado una reflectividad mucho menor debido al aumento de la rugosidad de la superficie general. Como se mencionó anteriormente, un mayor número de superposición aumenta la absorción de luz. A partir de estos valores teóricos, se encontró el máximo en cada caso, y este valor se utilizó para determinar un coeficiente de reflectividad preciso.

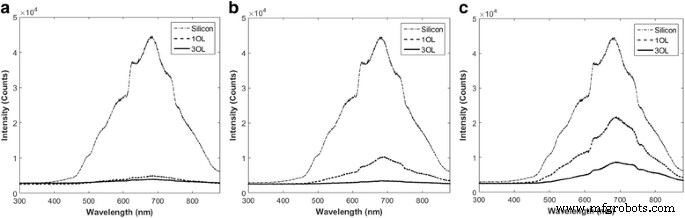
Reflexión de la luz de muestras de silicio tratadas con láser en uno y tres solapamientos (OL) y en espacios de a 0,025, b 0.10 y c 0,15 mm

También se estudiaron los efectos del espaciado de líneas sobre la reflectividad (Fig. 5). Comparando los resultados de una superposición, el aumento en el espaciado de líneas resultó en una reflectividad mucho mayor. Como era de esperar, el silicio poroso y fibroso absorbió más luz que el silicio mostrando signos de micropartículas solo. En espaciamientos de línea más grandes, porciones de silicio no se sometieron a ablación con láser; en cambio, quedaron micropartículas que descansaban sobre una superficie más lisa, que exhibía propiedades reflectantes más parecidas a las del silicio sin procesar.

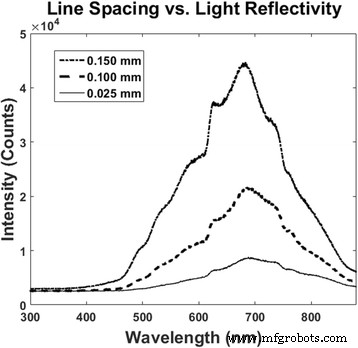
Reflejo de luz de muestras de silicio tratadas con láser en un solapamiento (OL) y espaciamientos de línea de 0.025, 0.10 y 0.15 mm

Una vez que la luz incidente ingresa al material, la absorción causa una reducción en la intensidad de la luz a medida que aumenta la profundidad según el coeficiente de absorción del material, α . Suponiendo un material uniforme con una constante α , la intensidad, yo , decae con profundidad z sigue la ley de Beer-Lambert, donde I ₀ representa la intensidad dentro de la superficie después de considerar las pérdidas por reflexión [24].

$$ I (z) ={I} _0 {e} ^ {\ hbox {-} \ alpha z} $$ (1)

La ablación con láser depende en gran medida de la transferencia de calor al material. Con láseres de nanosegundos, generalmente se supone que la mayor parte de la absorción se debe a interacciones de fotones individuales. Los aumentos en la absorción de luz dan como resultado temperaturas y presiones de la pluma más altas [25], que fomentan la formación de estructuras nanofibrosas.

Cuando la tasa de termalización es mayor que la tasa de excitación inducida por láser, el proceso se denomina fototérmico o pirolítico, donde se supone que la energía láser absorbida se transforma directamente en calor. Este es el caso cuando los tiempos de pulso del láser son mayores que el rango de nanosegundos. El procesamiento fototérmico nos lleva al modelado del flujo de calor a través del material. Su respuesta al láser se debe a efectos térmicos en sus coordenadas temporales y espaciales y puede modelarse a partir de derivaciones de la ecuación de calor.

Para determinar matemáticamente las relaciones de temperatura promedio esperadas entre las superficies de la muestra, la temperatura máxima, T , que ocurre al final del pulso láser ( t _p ), se determina mediante un modelo unidimensional de la siguiente manera [12, 26, 27]:

$$ T \ left (0, \ {t} _p \ right) =\ sqrt {\ frac {2 a} {\ pi ^ 3 {t} _p} \ frac {4 K \ left (1- R \ right) P} {kf {d} ^ 2}} $$ (2)

La duración del pulso láser ( t _p ) en nuestro caso fue de 57,5 ​​ns, con un diámetro de mancha ( d ), 20 μm a una frecuencia (f) de 100 kHz y una potencia media ( P ) de 12 W. El coeficiente de difusión térmica ( a ) –– para el silicio se estableció en 0.000085 m ² / s el coeficiente de energía residual K se fijó en una constante de 0,8 para el silicio, y la conductividad térmica k a 155 W / mK. R en este caso son los valores de reflectividad determinados experimentalmente anteriormente. A partir de esto, la temperatura media de la superficie después de n pulsos se calculó de acuerdo con la Ec. 3 a continuación, donde α es una constante de la raíz cuadrada de la frecuencia multiplicada por la duración del pulso (\ (\ alpha =\ sqrt {t_p f} \)) [12, 26, 27].

$$ {\ overline {T}} _ n =2 \ alpha \ frac {\ left [1- \ frac {2} {3} \ alpha \ right]} {\ left (1 + {\ alpha} ^ 2 \ right )} \ frac {T_m} {\ left (1- \ alpha \ right)} \ left [1+ \ frac {\ alpha ^ n- \ alpha} {n \ left (1- \ alpha \ right)} \ right ] $$ (3)

Usando las ecuaciones anteriores. 2 y 3 y asumiendo que no hay evaporación de partículas, se generaron gráficos de las temperaturas superficiales promedio alcanzadas por las muestras para espaciamientos de línea de 0.025, 0.10 y 0.15 mm en uno y tres solapamientos como se ve en la Fig. 6.

Temperaturas medias teóricas alcanzadas por muestras de silicio monocristalino sometidas a ablación con láser después de un número determinado de pulsos en un solo punto

A partir de los perfiles de temperatura que se muestran en la Fig. 6, hay un gradiente que se forma antes de que se alcance la temperatura media máxima. Este gradiente provoca la formación del plasma mencionado anteriormente. Se determinaron los valores máximos de estado estacionario para cada una de las muestras y, como se concluyó, las muestras en tres superposiciones alcanzaron una temperatura superficial promedio más alta que las de una superposición. Esto puede explicarse por el aumento en el tamaño de las nanopartículas, lo que conduce a mayores absorciones. Las únicas excepciones son las muestras con un espaciado de línea de 0.025 mm, donde ambas muestras dieron como resultado la misma temperatura promedio máxima. Esto se debe a la estrecha correlación de sus valores de reflectividad.

El número medio de partículas evaporadas de la superficie por pulsos sucesivos se estimó teóricamente en función de los parámetros de procesamiento del láser y las propiedades del material. La tasa de evaporación, R _evp , por ablación de pulso único se calcula en el modelo unidimensional de la siguiente manera [20, 27]:

$$ {\ left \ langle {R} _ {\ mathrm {evp}} \ right \ rangle} _ {\ mathrm {therm}} ={n} _ {\ mathrm {air}} {\ left (\ frac { A {k} _B {a} ^ {\ frac {1} {2}} {t} _p ^ {\ frac {1} {2}} {t} _ {\ mathrm {eq}} {P} _ { \ mathrm {avg}}} {M_a k {\ pi} ^ {\ frac {3} {2}} {R} _ {\ mathrm {rep}} {A} _ {\ mathrm {foc}}} \ right )} ^ {1/2} $$ (4)

Aquí, n _aire es la densidad del aire (kg / m ³ ), A es el coeficiente de absorción, t _eq es el tiempo de equilibrio, P _prom es la potencia media, M _a es la masa atómica (kg), A _foc es el área focal, R _{representante} es la frecuencia y k _B es la constante de Boltzmann (J / K). Usando esto y convirtiendo la tasa en un número de átomos basado en la masa atómica del silicio, el número promedio de partículas evaporadas se puede estimar como [20, 27]

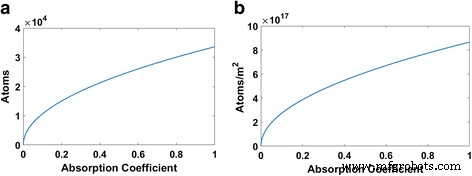
$$ {N} _ {\ mathrm {MP}} ={R} _ {\ mathrm {evp}} {R} _ {\ mathrm {rep}} {A} _ {\ mathrm {foc}} {D} _t $$ (5)

Los parámetros utilizados en este caso fueron los descritos en la ecuación anterior; sin embargo, el tiempo de equilibrio, t _eq se estableció en 1,5 × 10 ¹⁰ s, la frecuencia láser R _{representante} a 100 kHz, el tiempo de permanencia del pulso D _t calculado a partir del número efectivo de pulsos y, finalmente, el área focal A _foc se calculó a partir del diámetro mínimo teórico del punto láser. Se determinaron valores tanto para la tasa de evaporación como para el número estimado de partículas evaporadas a diferentes coeficientes de absorción láser. Los resultados se muestran gráficamente en la Fig. 7.

Número teórico de átomos evaporados por pulsos únicos y sucesivos con coeficientes de absorción variables. un número de átomos evaporados por pulsos sucesivos; b número de átomos evaporados por ablación por pulso

A medida que aumenta la absorción, el número medio de partículas y la velocidad comienzan aumentando aparentemente de forma parabólica. Hay un rápido aumento en el número de partículas evaporadas a valores de absorción más bajos. Aunque se puede lograr un mayor número de átomos a medida que aumenta la absorción, la curva ya no crece tan rápidamente. Esto explica por qué las superficies procesadas con láser de silicio con coeficientes de absorción más altos tienen más probabilidades de tener nanopartículas y formaciones de fibras a medida que aumenta el número de átomos evaporados, lo que permite una mayor reordenación estructural.

Proyección de oro de nanofibras de óxido de silicio generadas por láser

Las muestras preparadas a una potencia media de 12 W y con un espaciado de línea de 0,025 mm se pulverizaron con oro para evaluar sus propiedades conductoras. Las muestras se pulverizaron con oro durante 4 u 8 minutos. Los efectos de la conductividad y el tamaño de las partículas se midieron y compararon en diferentes superposiciones.

En estudios anteriores, se ha demostrado que el recubrimiento oxidado influye notablemente en la biocompatibilidad al aumentar la adsorción de grupos hidroxilo, lipoproteínas y glicolípidos. La Fig. 8 muestra los resultados de EDX y TEM de las muestras de silicio sometidas a ablación de 0,025 mm. Se observa que las concentraciones de oxígeno aumentan al aumentar los números de superposición (a – c), lo que sugiere una mayor biocompatibilidad. El recuento más alto de oxígeno se observa en la muestra con la mayor absorción, es decir, en cinco solapamientos (c). A medida que aumenta la generación de nanofibras, la temperatura promedio general y el número de átomos evaporados de una muestra, hay más partículas que interactúan con el aire ambiente en el que se realiza la ablación. Esto da como resultado partículas ricas en oxígeno debido a las reacciones de oxidación que ocurren dentro de la pluma del láser.

Imágenes EDX de silicio procesado con láser a 0,025 mm. un 1 OL, b 3 OL, c 5 OL, d TEM de muestra preparada en cinco superposiciones (OL)

Las imágenes SEM se analizaron usando ImageJ para determinar los diámetros aproximados de las fibras que ocurren en el espaciado de línea de 0.025 mm. Como se indica en la Fig. 9, los diámetros de las fibras crecen a medida que se añaden superposiciones. Por lo anterior, sabemos que los niveles de oxígeno aumentaron con la adición de superposiciones, lo que explica parcialmente el crecimiento en tamaño de las fibras.

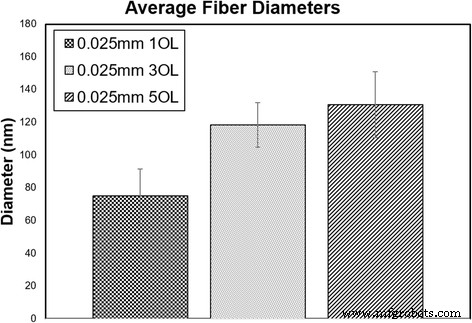
Diámetros de fibra promedio calculados a partir de imágenes SEM en una, tres y cinco superposiciones (OL)

A través de imágenes TEM, se calcularon los diámetros promedio de las partículas de oro y silicio junto con sus desviaciones estándar. A medida que aumentaba el número de superposiciones, se descubrió que también aumentaba el diámetro medio de las partículas de silicio. Esto concuerda tanto con la teoría de que el crecimiento de partículas se produce al aumentar la absorción como con los resultados anteriores que muestran la expansión de los diámetros de las fibras con superposiciones adicionales. El aumento del diámetro de la fibra puede explicarse por los tamaños crecientes de partículas del silicio. Como se muestra en la Fig. 10, la muestra con cinco solapamientos y un espaciado de línea de 0.025 mm tiene las partículas de silicio más grandes en comparación con las muestras con espaciamientos de línea más cortos. Esta es también la muestra con el valor de absorbancia más alto en comparación con las otras dos muestras. Esto explica los diámetros de fibra más grandes que se ven en la muestra b de la figura en comparación con la muestra a. La muestra que se muestra en c tiene un coeficiente de absorbancia que se encuentra entre los de las muestras ayb, lo que explica su crecimiento de partículas en comparación con el de las otras dos muestras.

Diámetros promedio de partículas de silicio de muestras de oro pulverizadas durante 8 min. un 1 OL 0,025 mm, b 5 OL 0,025 mm, c 5 OL 0,15 mm

En la Fig. 11, se muestra que los diámetros de las partículas de oro tienen un patrón de crecimiento muy similar al de las partículas de silicio. A medida que aumenta el número de superposición, se observa que los diámetros de las partículas de oro también aumentan.

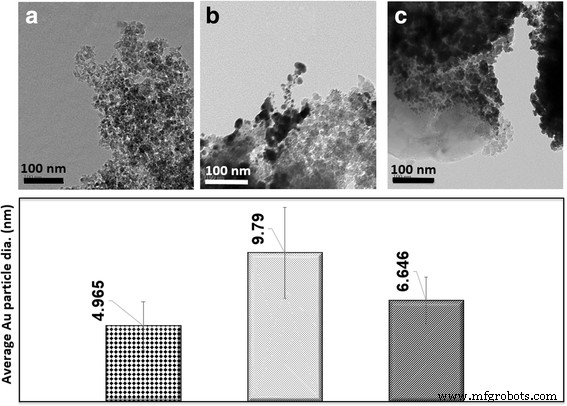
Diámetros medios de partícula de oro en nanómetros de muestras de oro pulverizadas durante 8 min. un 1 OL 0,025 mm, b 5 OL 0,025 mm, c 5 OL 0,15 mm

La concentración de oro en cada muestra se estimó utilizando el software ImageJ (Fig. 12). Se encontró que las concentraciones disminuían a 0.025 mm al pasar de una a cinco superposiciones. A partir de las imágenes SEM y los diámetros de fibra, la muestra de silicio en una superposición y un espaciado de línea de 0,025 mm tiene fibras más delgadas y, por lo tanto, espacios menos empaquetados. Esto permitiría que cayeran más partículas de oro entre estos espacios y se unieran por separado alrededor de las fibras en lugar de aglomerarse. En cinco superposiciones, las fibras son mucho más gruesas y el espacio entre ellas es más pequeño, lo que permite que se depositen menos partículas de oro en las grietas. Con un espaciado de línea de 0,15 mm y cinco superposiciones, la concentración cayó entre la de las dos muestras discutidas anteriormente como se muestra en la Fig. 10. Cuando se comparan los espacios de línea, un aumento en este último da como resultado una disminución en las concentraciones de oro. La reducción hace que la absorbancia del material disminuya y, por lo tanto, reduce el crecimiento de partículas. En cinco superposiciones, la concentración de oro aumenta cuando aumenta el espaciado porque la superficie es más suave (área de contacto general más pequeña), lo que da como resultado una mayor concentración de oro en las estructuras nanofibrosas sintetizadas.

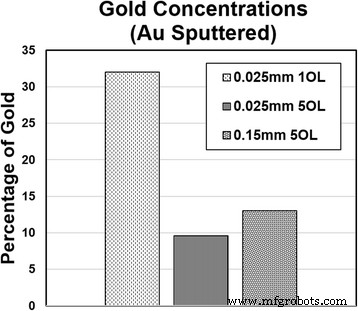
Concentraciones de oro encontradas en silicio procesado con láser pulverizado con oro durante 8 min a 1 OL 0.025 mm, 5 OL 0.025 mm y 5 OL 0.15 mm

En teoría, las duraciones de pulso más largas y la mayor densidad y temperatura de la pluma dan como resultado una formación de nanoestructuras más grandes. Nanostructure sizes depend highly on the plume diffusion time scale while their type depends on the density of the evaporated atoms. For this reason, to achieve nanofibrous structures, the laser pulses must be kept continuous for the plume density to remain at the critical level required for their formation. Hence, the larger particle sizes with growing overlaps can be explained in this fashion due to the higher overall surface temperatures and absorption coefficients [24].

The overall conductivity was measured through impedance spectroscopy for samples with one and two overlaps at a line spacing of 0.025 mm. The conductivity was measured using larger square samples of approximately 1.5 × 1.5 cm and connected directly to the spectrometer (in order to minimize the contact resistance). The Bode diagrams (an absolute total resistance as the function of AC frequency) were used to calculate the specific conductivity of films (in Siemens per centimeter, S/cm) after standardization to their thickness and area. Fig. 13 shows the clear distinction between overlaps and their conductivity. Since gold is a highly conductive element, it is expected that a sample containing more of it would have an enhanced conductivity. Previous studies developing a transistor have found that gold nanoparticles resulted in improved electrical performances [15]. The sample sputtered for 8 min with gold resulted in a higher conductivity than that sputtered for only 4 min. Samples with two overlaps are shown to have a lower conductivity than samples with one overlap as shown in Fig. 13. As previously denoted, the gold concentration decreased with increasing overlaps, hence explaining the reduction in conductivity. This is also supported in previous studies using gold sputtering techniques on glass, where the sheet resistance of the latter decreased exponentially with increasing sputtering time [28]. Since air is a poor conductor of electricity, it is expected that the samples with two overlaps would have a lower conductivity due to their increased oxygen concentrations previously determined from the EDX results.

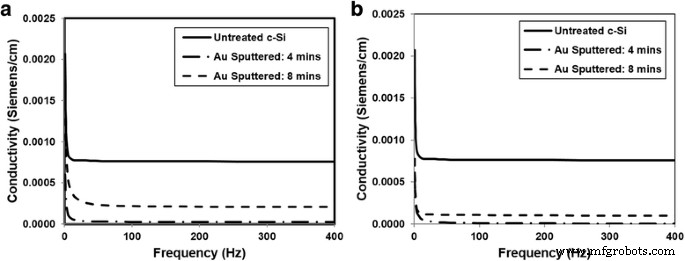
The total conductivity of gold sputtered silicon samples. un 1 OL, b 2 OL (higher conductivity of untreated silicon is due to its zero porosity)

Most of the conduction can be explained through quantum effects due to the dispersion and distance between the gold particles. Assuming the particles are of a spherical shape and the matrix is insulating, then the volume fraction can be determined as in Eq. 6, where R _c is the conductive particle radius, R _i the insulating particle radius, and n _c and n _i are the number of conductive and insulating particles, respectively [29].

$$ P=\frac{n_c{R}_c^3}{n_c{R}_c^3+{n}_i{R}_i^3} $$ (6)

The previous measurements of particle sizes acquired from the TEM images were used to determine the volume fraction of the conductive phase, P . These results can then be used in conjunction with Eq. 7 to determine the theoretical interparticle distances, l , assuming spherical conductive particles and a uniform size distribution [30].

$$ l={R}_c{\left[\frac{4\pi}{3 P}\right]}^{1/3}-2 $$ (7)

The interparticle distance can then be related directly to the conductivity of the silicon oxide σ _i and gold particles σ _c as in Eq. 8 below [31].

$$ {\sigma}_i={\sigma}_c{e}^{-2{X}_t l} $$ (8)

Where is X _t defined as in Eq. 9, with m being the mass of the charge carriers, V (t ) the temperature modified barrier height, and h is Planck’s constant.

$$ {X}_t={\left[\frac{8{\pi}^2 mV(t)}{h^2}\right]}^{0.5} $$ (9)

Assuming constancy of the parameters in X _t , the effect on the conductivity of the silicon oxide becomes highly dependent on the distance between the conductive particles. As one would expect from the equations, higher numbers and larger particle radii of conductive particles results in a higher volume fraction, which in turn results in increases in interparticle distances. From the measured particle sizes depicted earlier in Fig. 11, the relationship between the gold particle radii and the conductivity agree with the theoretically proposed relationships. The greater the distance between the conductive gold particles, the lower the overall conductivity of the silica. As seen in Fig. 14, the gold particle distances increase with a decrease in overlap, further agreeing with the conductivity measurements expected.

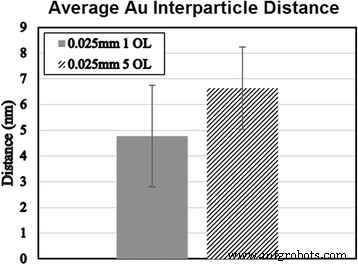
Experimental interparticle distances of gold sputtered silicon samples for 1 OL and 5 OL

Conclusions

In this report, a method of nanofiber generation using a nanosecond pulsed laser is proposed along with a technique to customize the electrical properties of laser processed silicon to improve its viability in sensing applications requiring a biocompatible environment using gold sputtering techniques. Micro and nanofibrous structures were achieved using a nanosecond Nd:YAG pulsed laser system on a single crystalline silicon wafer. Laser pulses enable to precisely deliver large amounts of energy into the surface of a material in order to achieve a desired nanofibrous structures. For silicon as an opaque material, the laser energy is absorbed near the surface, synthesizing thin-film of nanofibrous silicon without altering the bulk properties. The processed silicon samples were sputtered with gold for duration of either 4 or 8 min to impart and compare its effects on the conductive properties. Overlap number and line spacing were varied in this experiment, and the changes in the absorption capabilities of the samples were experimentally measured and compared. The absorption was found to increase at smaller line spacings and at higher overlaps, allowing for the rearrangement of the silicon substrate into fibers and agglomerates capable of absorbing more light. It was shown that both gold and silicon particles exhibited growth as the absorption coefficients of the materials increased. Fibrous structures were seen to form at shorter line spacings and at higher powers. As the overlap numbers were increased, the fiber diameters grew as well due to the growth in particle sizes. Finally, the conductivity showed some controllability in terms of the duration of sputtering undergone by the samples.

Identifying the fabrication technique for such biocompatible sensor devices is vital and is still being in progress. More studies, in current future direction of this project, need to be conducted to distill the proposed method and propose the guidelines to ascertain the scientific challenges as well as the prerequisites to make this technology market-viable. Although there is yet more research to be done in this area, these findings act as an important preliminary review as to the direction in which biological sensing surfaces can be further adapted and made cost effective. Silicon, being a semiconductor and one of the most common resource for electronic and circuit building, can now impart conductive and biocompatible properties. This method outlines an economic, simple, and yet effective way to process silicon to achieve nanofibrous structures able to increase its biocompatibility while still allowing for electrical conductance.

Investigaciones de la sorción de iones de metales pesados ​​utilizando nanocompuestos de biocarbón modificado con hierro El estudio de un nuevo sistema micelar similar a un gusano mejorado con nanopartículas