home Tecnología de fabricación Equipo de fabricación
Manufactura industrial
Internet industrial de las cosas | Materiales industriales | Mantenimiento y reparación de equipos | Programación industrial |
home  MfgRobots >> Manufactura industrial >  >> Industrial materials >> Nanomateriales

Estudios teóricos sobre fotodiodos de avalancha de InGaAs / InAlAs SAGCM

Resumen

En este documento, proporcionamos una visión detallada de los fotodiodos de avalancha de absorción, clasificación, carga y multiplicación separados de InGaAs / InAlAs (SAGCM APD) y se construye un modelo teórico de APD. A través del análisis teórico y la simulación bidimensional (2D), se comprende completamente la influencia de la capa de carga y el efecto de túnel en los APD. El diseño de la capa de carga (incluido el nivel y el espesor de dopaje) puede calcularse mediante nuestro modelo predictivo para diferentes espesores de multiplicación. Encontramos que a medida que aumenta el grosor de la capa de carga, disminuye el rango de nivel de dopaje adecuado en la capa de carga. En comparación con la capa de carga más delgada, el rendimiento de APD varía significativamente a través de varias desviaciones porcentuales de las concentraciones de dopaje en la capa de carga más gruesa. Además, la tasa de generación ( G btt ) del túnel de banda a banda y se analizó la influencia del efecto de túnel en el campo de avalanchas. Confirmamos que el campo de avalancha y el factor de multiplicación ( M n ) en la multiplicación disminuirá por el efecto de túnel. El modelo teórico y el análisis se basan en InGaAs / InAlAs APD; sin embargo, también son aplicables a otros sistemas de materiales APD.

Antecedentes

En 0.53 Ga 0,47 Los fotodiodos de avalancha (APD) (denominados en lo sucesivo InGaAs) son los fotodetectores más importantes para la detección de infrarrojos de onda corta. Son importantes en los campos tradicionales, como la comunicación por fibra óptica, las aplicaciones de reconocimiento y la teledetección. InP e In 0.52 Al 0,48 As (en adelante, InAlAs) tienen el mismo espaciado de celosía con InGaAs y excelentes características de ruptura de avalanchas; por lo tanto, son los materiales de capa de multiplicación adecuados de los APD de InGaAs en las aplicaciones tradicionales. En los últimos años, debido al rápido desarrollo de la detección de fotón único en la distribución de clave cuántica [1], la espectroscopia resuelta en el tiempo [2], la inspección del circuito óptico VLSI [3] y el alcance láser 3D [4], los APD son la clave componente en estas aplicaciones han atraído una atención creciente [5, 6]. Pellegrini y col. describieron el diseño, fabricación y rendimiento de dispositivos InGaAs / InP de geometría plana que se desarrollaron para la detección de fotón único con una eficiencia de detección de fotón único (SPDE) del 10% a 1550 nm (200 K) [7]. Tosi y col. presentó los criterios de diseño de un nuevo fotodiodo de avalancha de fotón único (SPAD) de InGaAs / InP con SPDE alto (30%, 225 K), bajo ruido y baja fluctuación de tiempo [8]. En la simulación, se construyó un modelo de dispositivo basado en datos experimentales para predecir la tasa de recuento oscuro (DCR) y SPDE de InGaAsP / InP SPAD en [9], y una plataforma de simulación integrada que puede evaluar el rendimiento de distribución de claves cuánticas de estado señuelo de InGaAs / InP SPAD se construyó en [10]. Acerbi y col. presentó criterios de diseño para APD de fotón único InGaAs / InP con un simulador SPAD personalizado [11]. Para los APD InGaAs / InAlAs, se demostró que una estructura mesa SPAD InGaAs / InAlAs alcanza el SPDE del 21% (260 K); sin embargo, se observó una DCR alta y se atribuyó a una corriente de túnel excesiva [12]. Luego, [13] utilizó una capa gruesa de avalancha de InAlAs en los APD de InGaAs / InAlAs para mejorar el SPDE (26%, 210 K) y disminuir el DCR (1 × 10 8 Hz). En la simulación de APD basados ​​en InAlAs, se estableció un modelo de dispositivo basado en el método Monte Carlo para estudiar la caracterización básica de los APD InGaAs / InAlAs en [14], y la influencia de la capa de carga y la capa de multiplicación en el voltaje de traspaso y la ruptura. Los voltajes se estudiaron con simulaciones numéricas 2D en estado estacionario en [15].

En comparación con los APD basados ​​en InAlAs, las investigaciones de los APD basados ​​en InP son más completas y profundas en teoría y simulación. Sin embargo, el APD basado en InAlAs se utiliza cada vez más en lugar de InP, ya que tiene una banda prohibida más grande que puede mejorar las características de ruptura tanto en los APD como en los SPAD [16]. La relación del coeficiente de ionización del electrón (α) al agujero (β) en InAlAs es mayor en comparación con InP y, por lo tanto, tiene un factor de ruido en exceso bajo y un producto de ancho de banda de alta ganancia. Además, InAlAs exhibe un gran aumento en la probabilidad de ruptura con el índice de overbias, lo que hace que los SPAD de InAlAs tengan una DCR más baja [17]. Algunas propiedades y conclusiones importantes con respecto a los APD basados ​​en InAlAs se obtuvieron de estudios previos, como el bajo exceso de ruido que se puede lograr en estructuras de InAlAs con regiones de avalancha gruesas y delgadas [18]. El campo eléctrico del umbral de tunelización en la absorción (InGaAs) es 1.8 × 10 5 V / cm, y la corriente de túnel se convierte en el componente dominante de la corriente oscura en el campo alto [14]. Una estructura de iluminación vertical tiene una tolerancia óptica mayor, pero tiene una compensación más seria entre el tiempo de tránsito de la portadora y la capacidad de respuesta [19]. Además, el modelo teórico, la estructura (espesor y dopaje), el campo eléctrico y otros parámetros de APD basados ​​en InAlAs se han estudiado en [20, 21, 22]. Sin embargo, estos estudios solo se centraron en las influencias de los parámetros de estructura de APD comunes, como el espesor de la capa de absorción, el espesor de multiplicación y el nivel de dopaje de la capa de carga. La relación entre los parámetros de estructura y el rendimiento del APD basado en InAlAs aún no se ha entendido ni optimizado por completo.

En este artículo se investigó un estudio teórico y un análisis de simulación numérica basado en la estructura vertical de InGaAs / InAlAs para detección de longitud de onda de 1,55 μm. Construimos un modelo teórico para estudiar la influencia de los parámetros de la estructura en el dispositivo y la relación detallada de cada capa en los APD. Se analizaron y simularon el diseño de la capa de carga con diferentes espesores de multiplicación, la influencia del espesor en el nivel de dopaje en la capa de carga y el efecto tunelizador en el campo de avalanchas en la multiplicación.

Métodos

En esta sección, se construyó una relación matemática entre los parámetros del dispositivo y la distribución del campo eléctrico en el dispositivo, que se aplicó para analizar la capa de carga y el efecto de túnel. Al mismo tiempo, se construyó un modelo de simulación que incluía estructura de simulación, parámetros de material y modelos físicos básicos. El modelo de análisis teórico y el modelo de simulación se basaron en la estructura vertical de SAGCM InGaAs / InAlAs APD.

Modelo teórico y análisis de la capa de carga

Los parámetros del dispositivo, como el nivel de dopaje, el espesor, los materiales y la estructura, se utilizaron para construir el modelo matemático para calcular la distribución del campo eléctrico en APD. Las teorías físicas básicas que incluyen la ecuación de Poisson, el modelo de capa de agotamiento y el modelo de unión PN del dispositivo semiconductor se pueden encontrar en los capítulos 1, 2 y 4 en [23] y [24]. La ecuación del factor de multiplicación de la unión se puede encontrar en [25], y los parámetros de material del semiconductor son de [26]. El modelo presentado adopta la ecuación de Poisson, la ecuación de densidad de corriente de túnel, el modelo de capa de agotamiento, el modelo de teoría de la unión y el modelo local de ganancia de avalancha. El sistema de coordenadas matemático simplificado del APD que incluye parámetros de estructura básica (materiales, espesor, dopaje y constante dieléctrica) se presenta en la Fig. 1. Es una estructura APD SACM simplificada que ignora la capa de clasificación. Los materiales de la capa de contacto, la capa de carga y la capa de multiplicación son InAlAs y la capa de absorción es InGaAs. Las uniones de capas están separadas por X n , 0, X m , X c y X a y X p por la x coordinar. Los niveles de dopaje se expresan con N 0 , N 1 , N 2 , N 3 y N 4 , los espesores de capa se expresan mediante w 0 , w 1 , w 2 , w 3 y w 4 , y las constantes dieléctricas se expresan mediante ε s0 , ε s1 , ε s2 , ε s3 y ε s4 de contacto A, multiplicación, carga, absorción y contacto B, respectivamente.

El sistema de coordenadas matemático simplificado de SACM InGaAs / InAlAs APD. Presenta las estructuras simplificadas de un APD que se utiliza para construir un modelo teórico. El sistema de coordenadas matemático simplificado del APD que incluye parámetros de estructura básica (materiales, espesor, dopaje y constante dieléctrica)

La ecuación 1 es la ecuación de Poisson, que puede resolver la distribución de potencial eléctrico utilizando la densidad de carga ρ . En esta ecuación, ρ es igual al ion dopante N en el modelo de capa de agotamiento, w es igual al grosor de la capa de agotamiento, y ε es la constante dieléctrica del material. En el modelo común de distribución del campo eléctrico de la unión PN, ρ es una variable que depende del espesor de la capa de agotamiento w e ion dopante N . En este modelo, cambia después de considerar el efecto de túnel. Sin embargo, antes de considerar el efecto de túnel, primero construimos la distribución del campo eléctrico usando un método común.

$$ \ frac {d \ xi} {d x} =\ frac {\ rho} {\ varepsilon} =\ frac {q \ times N} {\ varepsilon} $$ (1)

Al resolver la ecuación de Poisson con los parámetros del dispositivo, se obtiene la expresión matemática del campo eléctrico máximo. Esta expresión está determinada por la variación del espesor de penetración en la capa de agotamiento que se muestra en las fórmulas 2 y 3. En esta expresión, los parámetros que incluyen los niveles de dopaje ( N ), espesores de la capa de agotamiento ( w ) y constantes dieléctricas ( ε) de diferentes capas se puede encontrar en la Fig. 1.

$$ {\ xi} _ {\ max (w)} ={\ sum} _ {k =1} ^ 4 \ left (- \ frac {q \ times {N} _k \ times {w} _k} {\ varepsilon_ {sk}} \ right) $$ (2) $$ {\ xi} _ {\ max (w)} =\ frac {q \ times {N} _0 \ times {w} _0} {\ varepsilon_ {s0 }} $$ (3)

Luego, la distribución del campo eléctrico se puede derivar en todos los puntos usando las fórmulas 4 y 5. La condición de contorno ignora el potencial incorporado V br en la Fórmula 6; por lo tanto, se puede calcular la relación matemática entre el espesor de la capa de agotamiento y el voltaje de polarización.

$$ {\ xi} _ {\ left (x, w \ right)} ={\ xi} _ {\ max (w)} + {\ sum} _ {k =1} ^ 4 \ left (\ frac { q \ times {N} _k \ times \ left | x \ right |} {\ varepsilon_ {sk}} \ right) \ left ({X} _p Finalmente, la relación matemática entre la distribución del campo eléctrico y el voltaje de polarización en el dispositivo se obtiene usando las fórmulas 7-11:

$$ \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _1 \ times \ left | x \ right |} {\ varepsilon_ {s1}} \ left (0 \ ge x \ ge {X} _m \ right) $$ (7) $ $ \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times \ left | x- {X} _m \ right |} {\ varepsilon_ {s2}} \ left ({X} _m \ ge x \ ge {X} _c \ right) $$ (8) $$ \ xi \ left (x, {V} _ {\ mathrm {sesgo} } \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} { \ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times {w} _2} {\ varepsilon_ {s2}} + \ frac {q \ times {N} _3 \ times \ left | x- { X} _c \ right |} {\ varepsilon_ {s3}} \ left ({X} _c \ ge x \ ge {X} _a \ right) $$ (9) $$ \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _1 \ veces {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ veces {N} _2 \ veces {w} _2} {\ varepsilon_ {s2}} + \ frac {q \ veces {N} _3 \ veces {w} _3} {\ varepsilon_ {s3}} + \ frac {q \ veces {N} _4 \ veces \ left | x- {X} _a \ right |} {\ varepsilon_ {s4}} \ left ({X} _a \ ge x \ ge {X} _p \ right) $$ (10) $$ \ xi \ left (x, {V} _ { \ mathrm {sesgo}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} - ​​\ frac {q \ times {N} _0 \ times x } {\ varepsilon_ {s0}} \ left (0 \ le x \ le {X} _n \ right) $$ (11)

A partir del modelo, una vez que el límite de la capa de agotamiento alcanza la región de contacto, se pueden utilizar las fórmulas 7-11 para analizar el campo eléctrico en cada capa. En el APD práctico, las capas de absorción y multiplicación se dopan involuntariamente en capas intrínsecas. N 3 y N 1 son menores que N 2 . Por lo tanto, la Fórmula 9 es aproximadamente igual a la Fórmula 12. Es la razón por la que la capa de carga puede controlar la distribución del campo eléctrico en el dispositivo.

$$ {\ Displaystyle \ begin {array} {l} \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times { w} _2} {\ varepsilon_ {s2}} + \ frac {q \ veces {N} _3 \ veces \ izquierda | x- {X} _c \ derecha |} {\ varepsilon_ {s3}} \\ {} \ kern4em \ approx {\ xi} _ {\ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times {N} _2 \ times {w} _2} {\ varepsilon_ { s2}} \ left ({X} _ {\ mathrm {c}} \ ge x \ ge {X} _a \ right) \ end {matriz}} $$ (12)

En la Fórmula 8, la diferencia del campo eléctrico entre la multiplicación y la absorción se determina utilizando el producto de N 2 y w 2 . N 2 es el nivel de dopaje en la capa de carga y w 2 es el espesor de la capa de carga. Para una distribución adecuada del campo eléctrico en InGaAs / InAlAs APD, el campo eléctrico en la capa de absorción (InGaAs) debe estar dentro de los valores de intervalo de 50-180 kV / cm que aseguren suficiente velocidad para los portadores fotoinducidos y eviten el efecto de túnel. en la capa de absorción [10]. Es decir, el campo de avalancha en la multiplicación debería disminuir a 50-180 kV / cm en absorción por la capa de carga. Por lo tanto, podemos usar la Fórmula 8 para encontrar el nivel de dopaje calculado óptimo y los espesores de la capa de carga. Cuando la capa de multiplicación es de 200 nm (el campo de avalancha E en la multiplicación es 6,7 × 10 5 V / cm mientras que la capa de multiplicación es de 200 nm [27]); los valores calculados de nivel de dopaje y espesor en la capa de carga se comparan con los resultados de [28,29,30,31,32,33] en la Fig. 2. La región de los valores teóricos concuerda bien con los datos experimentales. Este resultado prueba que la Fórmula 8 se puede utilizar para predecir el nivel de dopaje con diferentes espesores en la capa de carga cuando el espesor de multiplicación es seguro.

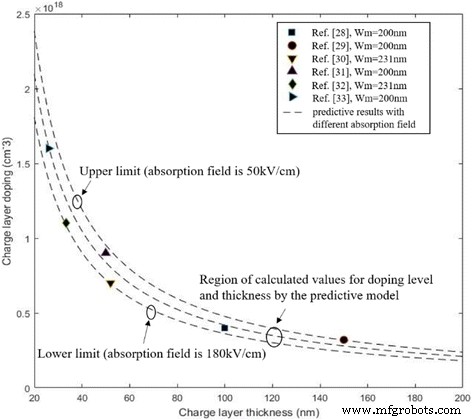
Comparación de resultados teóricos y datos de experimentos de varios informes ( w m =200 nm). Símbolos cerrados:el nivel de dopaje y el grosor de la capa de carga con un grosor de multiplicación de 200 nm (cuadrado negro, círculo negro, triángulo negro, triángulo negro que apunta hacia la derecha) y 231 nm (diamante negro, triángulo negro que apunta hacia abajo) en las referencias. Presenta los valores calculados de la capa de carga (nivel y espesor de dopaje) por la Fórmula 8 (el campo de absorción es 50-180 kV / cm). Cuando el campo de absorción es de 50 kV / cm, se puede obtener el límite superior del nivel de dopaje en la capa de carga. Cuando el campo de absorción es de 180 kV / cm, se puede obtener el límite inferior del nivel de dopaje en la capa de carga. Comparamos los resultados teóricos y los datos de experimentos de varios informes. La región de valores teóricos concuerda bien con los datos experimentales. Líneas discontinuas con los valores calculados de nivel y espesor de dopaje por la fórmula

Calculamos el nivel de dopaje óptimo para diferentes espesores de la capa de carga con la capa de multiplicación de 300, 500 y 700 nm, y los resultados se presentan en la Fig. 3. Este resultado ilustra que la tolerancia en el nivel de dopaje en la capa de carga es relacionado con su espesor y el rango de nivel de dopaje disminuye con el aumento de espesor en la capa de carga. Es decir, si aplicamos una región de carga gruesa, solo existiría un pequeño rango de nivel de dopaje en la capa de carga para satisfacer el campo eléctrico óptimo. Como resultado, el rendimiento de APD varía significativamente a través de varias desviaciones porcentuales de las concentraciones de dopaje en la capa de carga más gruesa. En la sección "Resultados y discusión", se simularon las estructuras prácticas de los APD para estudiar y verificar el análisis teórico, que incluye la influencia del espesor de la capa de carga en el rango del nivel de dopaje en la capa de carga y la variedad de rendimiento para diferentes espesores de capa de carga en APD.

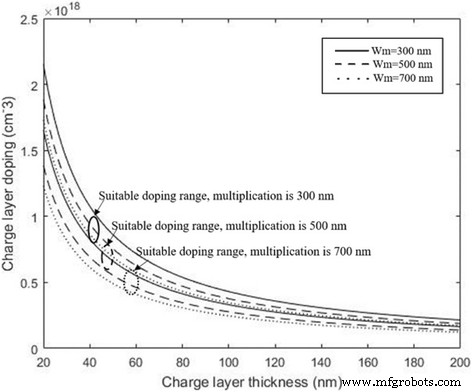
El nivel de dopaje y el grosor óptimos de la capa de carga para diferentes capas de multiplicación. Línea continua: w m =300 nm. Línea discontinua: w m =500 nm. Línea de puntos: w m =700 nm. Presenta los valores calculados de la capa de carga (nivel de dopaje y espesor) por la fórmula mientras que el campo de la capa de absorción es adecuado. Los espesores de la capa de multiplicación son 300, 500 y 700 nm. Cuando el grosor de la capa de multiplicación es seguro, podemos usar la fórmula para encontrar el nivel de dopaje óptimo y el grosor de la capa de carga

Modelo teórico con consideración de la construcción de túneles

El modelo de análisis anterior trata sobre la distribución del campo eléctrico en el dispositivo y se basa en la premisa de que ρ es el ion dopante en la capa de agotamiento. Si existe un campo eléctrico suficientemente alto dentro de la capa de absorción, la flexión de la banda local puede ser suficiente para permitir que los electrones formen un túnel [34]. Por lo tanto, puede producirse un túnel de electrones. A partir del diagrama esquemático de tunelización de la Fig.4, cuando la capa de absorción tiene un tunelización de ruptura, el efecto de tunelización cambia la densidad de carga ρ , la carga positiva en absorción aumenta y la carga negativa en las capas de multiplicación y carga aumenta. Por lo tanto, ρ no es igual a la densidad de carga de iones dopantes en la capa de agotamiento mientras aparece el efecto de túnel. Las fórmulas que se discutieron anteriormente cambiarán después de considerar el efecto de túnel.

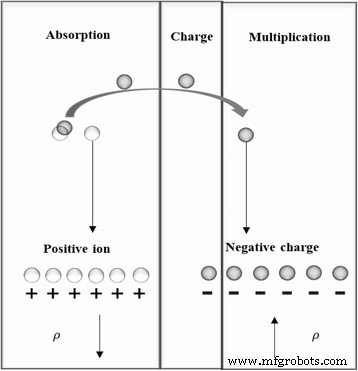
Proceso de tunelización y cambio de densidad de carga en las capas de multiplicación y absorción. Presenta un diagrama esquemático del proceso de tunelización en el dispositivo. Si existe un campo eléctrico suficientemente alto dentro de la capa de absorción, la curvatura de la banda local puede ser suficiente para permitir que los electrones formen un túnel. Cuando la capa de absorción tiene un túnel de ruptura, la carga positiva en la absorción aumenta y la carga negativa en las capas de multiplicación y carga aumenta. Por lo tanto, ρ no es igual a la densidad de carga de iones dopantes en la capa de agotamiento mientras aparece el efecto de túnel

La tasa de generación G bbt del túnel banda a banda se describe en la Fórmula 13 [35, 36].

$$ {G} _ {bbt} ={\ left (\ frac {2 {m} ^ {\ ast}} {E_g} \ right)} ^ {1/2} \ frac {q ^ 2 {E_p} ^ {\ gamma}} {{\ left (2 \ pi \ right)} ^ 3 {\ hbar} ^ 2} \ exp \ left (\ frac {- \ pi} {4 {q \ mathit {\ hbar E}} _p} {\ left (2 {m} ^ {\ ast} \ times {E_g} ^ 3 \ right)} ^ {\ raisebox {1ex} {$ 1 $} \! \ left / \! \ raisebox {-1ex} {$ 2 $} \ right.} \ Right) =A \ times {E_p} ^ {\ gamma} \ times \ exp \ left (- \ frac {B} {E_p} \ right) $$ (13)

En la Fórmula 13, E g es la banda prohibida de energía de InGaAs, m * (igual a 0,04 m e ) es la masa reducida efectiva, E p es el campo eléctrico de ruptura en la capa de absorción, y γ es un parámetro definible por el usuario que generalmente está restringido a 1 ~ 2. La A y B son los parámetros de caracterización. Calculamos el G bbt con diferentes γ , y los resultados se muestran en la Fig. 5. Se puede encontrar que G bbt adapta el mismo orden de magnitud para el nivel de dopaje de la capa de carga mientras que γ está restringido a 1 ~ 1.5.

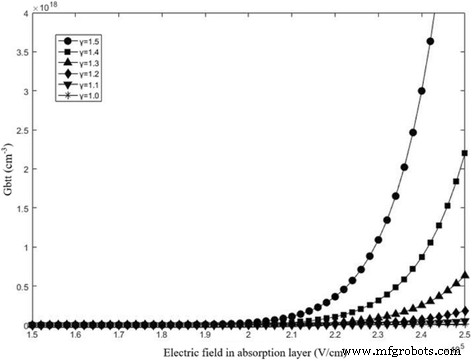
El G btt para diferentes campos en la capa de absorción con diferentes γ . Los valores de γ es 1.0 (estrella negra), 1.1 (triángulo negro que apunta hacia abajo), 1.2 (diamante negro), 1.3 (triángulo negro), 1.4 (cuadrado negro), 1.5 (círculo negro). Presenta los resultados calculados de G btt según la fórmula 13. Cuando el campo de absorción supera los 19 kV / cm, G bbt aumenta gradualmente. También se puede encontrar que G bbt adapta el mismo orden de magnitud para el nivel de dopaje de la capa de carga mientras que γ está restringido a 1 ~ 1.5

Como resultado, la densidad de carga ρ es una variable y está determinada por el efecto túnel y el ion dopante en el túnel de absorción. En esta ocasión, la Fórmula 1 se cambiará a la Fórmula 14 y el campo eléctrico en la capa de multiplicación será descrito por la Fórmula 15. w túnel es la capa de agotamiento efectiva del proceso de tunelización [35]. Por lo tanto, el cambio de campo de avalancha se puede describir mediante la Fórmula 16, y el campo de avalancha disminuirá en la multiplicación con el efecto de túnel.

$$ \ frac {d \ xi} {dx} =\ frac {\ rho} {\ varepsilon} =\ frac {q \ times \ left (N + {G} _ {btt} \ right)} {\ varepsilon}, {E} _p> 1.8 \ veces {10} ^ 5V / cm $$ (14) $$ \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) ={\ xi} _ { \ max \ left ({V} _ {\ mathrm {sesgo}} \ right)} + \ frac {q \ times \ left ({N} _1 \ times \ left | x \ right | + {G} _ {bbt } \ times {w} _ {\ mathrm {túnel}} \ right)} {\ varepsilon_ {s1}} \ left (0 \ ge x \ ge {X} _m \ right) $$ (15) $$ \ delta \ xi \ left (x, {V} _ {\ mathrm {sesgo}} \ right) =\ delta E =\ frac {q \ times {G} _ {btt} \ times {w} _ {\ mathrm {túnel }}} {\ varepsilon _ {\ mathrm {s} 3}} $$ (16)

Los coeficientes de ionización de electrones y huecos se describen mediante las fórmulas 17 y 18 en [18]. E es el campo de avalancha en la multiplicación.

$$ \ alpha ={a} _n {e} ^ {\ raisebox {1ex} {$ - {b} _n $} \! \ left / \! \ raisebox {-1ex} {$ E $} \ right.} $$ (17) $$ \ beta ={a} _p {e} ^ {\ raisebox {1ex} {$ - {b} _p $} \! \ Left / \! \ Raisebox {-1ex} {$ E $ } \ right.} $$ (18)

El efecto de la avalancha de portadores se explica por el modelo de ionización por impacto. Teniendo en cuenta la densidad de portadores extremadamente baja de la capa de multiplicación en comparación con la capa de carga, es razonable suponer que el campo eléctrico es uniforme en toda la capa de multiplicación. Por lo tanto, el factor de multiplicación ( M n ) se puede expresar como la siguiente ecuación. 19. Aquí, w m es el espesor de la capa de multiplicación y k es la relación del coeficiente de ionización por impacto definida por α / β . Desde k varía muy lentamente con el campo eléctrico, k es aproximadamente constante para una ligera variación de w m [37].

$$ {M} _n =\ frac {k-1} {k \ times {e} ^ {- \ alpha \ left (1- \ raisebox {1ex} {$ 1 $} \! \ Left / \! \ Raisebox { -1ex} {$ k $} \ derecha. \ Derecha) {w} _m} -1} $$ (19)

Suponiendo constante w m y voltaje de polarización, diferenciación de M n con respecto a los coeficientes de ionización de electrones está en las fórmulas 20 y 21.

$$ \ delta {M} _n \ left | {} _ {w =const \ &V =const} \ right. ={M_n} ^ 2 {e} ^ {- \ alpha \ left (1- \ raisebox {1ex} {$ 1 $} \! \ Left / \! \ Raisebox {-1ex} {$ k $} \ right. \ Right) {w} _m} \ times {w} _m \ delta \ alpha $$ (20) $$ \ delta \ alpha =\ frac {\ delta \ alpha} {\ delta E} ={\ alpha} _n {b} _n {e} ^ {\ frac {- {b} _n} {E}} \ frac {1 } {E ^ 2} $$ (21)

En las fórmulas 20 y 21, δα / δE es positivo. Se supone que el 20% de una capa de absorción de agotamiento total es w túnel y la capa de absorción tiene un espesor de 400 nm. Al resolver la Fórmula 16, la relación entre δE y el campo de absorción con diferentes γ se presenta en la Fig. 6. Se puede encontrar que δE adapta el mismo orden de magnitud para el campo de avalancha en la multiplicación. Por lo tanto, el efecto de túnel tiene una influencia en el campo de avalanchas y el M n disminuirá con el efecto tunel. En el análisis, asumimos que la carga negativa no se multiplica en la multiplicación y el modelo será más riguroso después de tomarlo en consideración. Para verificar y analizar la influencia del efecto de túnel en la estructura práctica de los APD, simulamos la relación entre el efecto de túnel y el campo de avalancha de multiplicación en detalle en la sección "Resultados y discusión".

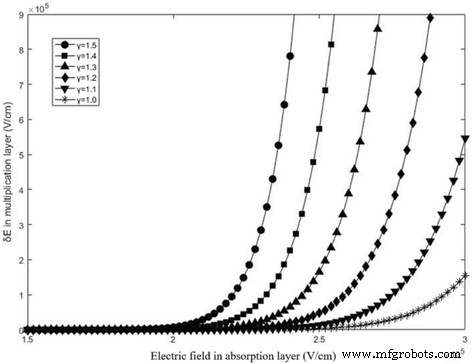
El δE para diferentes campos en la capa de absorción con diferentes γ . Los valores de γ es 1.0 (estrella negra), 1.1 (triángulo negro que apunta hacia abajo), 1.2 (diamante negro), 1.3 (triángulo negro), 1.4 (cuadrado negro), 1.5 (círculo negro). Presenta los resultados calculados de δE por la Fórmula 16. Cuando el campo de absorción excede los 19 kV / cm, δE aumenta gradualmente. También se puede encontrar que δE adapta el mismo orden de magnitud para el campo de avalancha en la multiplicación. Por lo tanto, el efecto de túnel tiene una influencia en el campo de avalanchas con el efecto de túnel

Estructura y modelo de simulación

Se utilizó una simulación de dispositivo semiconductor de TCAD para la simulación y el análisis. Este motor de simulación define modelos físicos en simulación y los resultados tienen un significado físico [20]. Los modelos físicos básicos se presentaron de la siguiente manera. Los modelos de deriva-difusión, incluidas las ecuaciones de continuidad de portadora y de Poisson, se utilizaron para simular la distribución del campo eléctrico y la corriente de difusión I DIFF . El modelo de tunelización banda a banda se utilizó para la corriente de tunelización banda a banda I B2B , y el modelo de tunelización asistida por trampa se utilizó para la corriente de tunelización asistida por trampa I TAT . La corriente de recombinación de generación I GR fue descrito por el modelo de recombinación Shockley-Read-Hall y la corriente de recombinación Auger I AUGER fue descrito por el modelo de recombinación Auger. La corriente oscura fue descrita claramente por esos mecanismos [38]. La multiplicación de avalanchas fue descrita por el modelo de ionización por impacto de Selberherr. Para el modelo de simulación se utilizaron otros modelos básicos, incluidas las estadísticas de portadora de Fermi-Dirac, la concentración de portadora dependiente, la movilidad de campo baja, la saturación de velocidad y los métodos de trazado de rayos, y se construyó un modelo de simulación riguroso.

Las estructuras de los dispositivos en la simulación fueron similares a las estructuras experimentales en [13]. La sección transversal esquemática del APD SAGCM InGaAs / InAlAs iluminado en la parte superior se muestra en la Fig. 7. Las estructuras de arriba a abajo se nombran secuencialmente como capa de contacto de InGaAs, capa de revestimiento de InAlAs, capa de clasificación de InAlGaAs, capa de absorción de InGaAs, clasificación de InAlGaAs capa, capa de carga de InAlAs, capa de multiplicación de InAlAs, capa de revestimiento de InAlAs, capa de contacto de InP y sustrato de InP. El espesor y el dopaje de cada capa también se presentan en la Fig. 7. Para evitar la influencia del espesor en los resultados de la simulación, elegimos dos estructuras de simulación. Una estructura de simulación se denomina APD-1 (las capas de multiplicación y absorción son 800 y 1800 nm, respectivamente), y la otra estructura de simulación se denomina APD-2 (las capas de multiplicación y absorción son 200 y 600 nm, respectivamente).

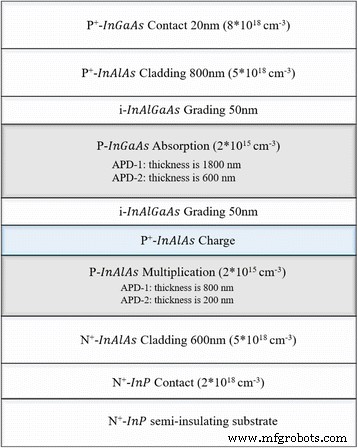
Estructura de simulación y parámetros del APD. Presenta la sección transversal esquemática de SAGCM InGaAs / InAlAs APD-1 y APD-2 con iluminación superior. Incluye estructura, materiales, dopaje y espesor

Para probar el modelo de simulación, los datos del experimento en [13] se compararon con los resultados de la simulación. En esta simulación, usamos la misma estructura en la referencia, y se dieron las características de corriente-voltaje del dispositivo. La Figura 8 muestra los resultados de nuestra simulación y los resultados del experimento en la referencia. Tienen un voltaje de perforación similar V pt y voltaje de ruptura V br . Además, los resultados de la simulación y el experimento se corresponden bien. Por lo tanto, el modelo de nuestra simulación es preciso. Los parámetros mencionados anteriormente se enumeran en la Tabla 1.

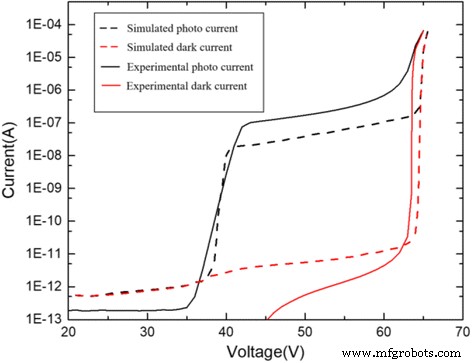
Resultados de la simulación comparados con los resultados del experimento (fotocorriente y corriente oscura). Línea discontinua negra:foto actual simulada. Línea discontinua roja:corriente oscura simulada. Línea continua negra:foto actual experimental. Línea sólida roja:corriente oscura experimental. Presenta la comparación de los resultados de la simulación y los resultados del experimento. El modelo de simulación utiliza los mismos parámetros del experimento en la referencia

Resultados y discusión

En esta sección, el análisis teórico y las conclusiones se estudiaron mediante simulación en detalle. En primer lugar, se estudió la influencia del espesor de la capa de carga en la tolerancia del nivel de dopaje en la capa de carga en la sección "Influencia del espesor de la capa de carga". Luego, la relación entre el efecto de túnel y el campo de avalancha de multiplicación se analizó y verificó en la sección "Efecto de túnel en la distribución del campo eléctrico".

Influencia del grosor de la capa de carga

De [14], una distribución de campo adecuada en InGaAs / InAlAs APD debe cumplir con esas reglas. La garantía V pt < V br y V br - V pt debe tener un margen de seguridad para procesar variaciones en las fluctuaciones de temperatura y rango de operación. En la capa de absorción, el campo eléctrico debe ser superior a 50-100 kV / cm para garantizar una velocidad suficiente para los portadores fotoinducidos. Paralelamente, el campo eléctrico debe ser inferior a 180 kV / cm para evitar el efecto de túnel en la capa de absorción. Electric field distribution greatly influences the device performance. The choice of electric field in the absorption layer has a balancing of the tradeoff between small transit time, dark current, and high responsivity for the practical requirement.

In the simulation, we used the structure of APD-1 (multiplication is 800 nm thick) and adjusted the charge layer thickness from 50 to 210 nm to study the influence of charge layer thickness on doping level range and verify the theoretical conclusions in analytical model. In the simulation, we selected different doping level ranges in the charge layer so that the electric field distribution complies with the rules. The simulation results on the relationship between thickness and doping level range in the charge layer are presented in Fig. 9a. As the charge layer thickness increases, the suitable doping level range in charge layer decreases. A relatively large doping level range exists in the thin charge layer, and under this doping level range, the device will have a suitable electric field distribution. Apparently, the doping level range is determined by charge layer thickness. The simulation result of APD-2 (with a thickness of multiplication of 200 nm) is presented in Fig. 9b, which has a similar result. Moreover, it can be found that the calculated results of Fig. 2 and simulation results of Fig. 9b match well as shown in Fig. 9c. The small difference between the calculated results and simulation results is caused by the different values of avalanche field in the simulation and calculation. The avalanche field in simulation engine is used 6.4 × 10 5  V/cm, while in the calculation, we use the value of 6.7 × 10 5  V/cm from [27].

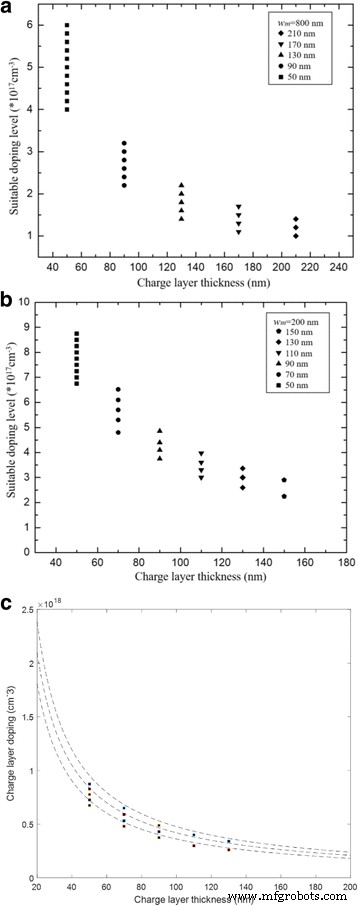
un Relationship between suitable doping level and thickness of charge layer (APD-1). The thickness of charge layer is 50 nm (black square), 90 nm (black circle), 130 nm (black triangle), 170 nm (black down-pointing triangle), 210 nm (black diamond). un presents the suitable doping level region for different thickness of charge layer. As the charge layer thickness increases, the suitable doping level range in the charge layer decreases. A relatively large doping level range exists in the thin charge layer, and under this doping level range, the device will have a suitable electric field distribution. Apparently, the doping level range is determined by charge layer thickness. b Relationship between suitable doping level and thickness of charge layer (APD-2). The thickness of charge layer is 50 nm (black square), 70 nm (black circle), 90 nm (black triangle), 110 nm (black down-pointing triangle), 130 nm (black diamond), and 150 nm (black pentagon). The figure description of b is similar to a . c Comparison of calculated results in Fig. 2 and simulated results in Fig. 9b. Dashed line:calculated results. Closed symbols:simulated results (black square). c presents the comparison of calculated results in Fig. 2 and simulated results in Fig. 9b. The calculated results and simulated results correspond well

The charge layer thicknesses of 210 and 50 nm (APD-1) were selected to show the simulation details and the influence of doping level on the electric field distribution. Figure 10a, c shows the current simulation results of different doping levels in thicknesses of 210 and 50 nm, respectively. Figure 10b, d shows the electric field distribution simulation results using the same structure. The simulation results show that thicknesses of 210 and 50 nm have doping level ranges of 1.0 × 10 17 –1.3 × 10 17  cm −3 and 3.9 × 10 17 –5.7 × 10 17  cm −3 , respectively.

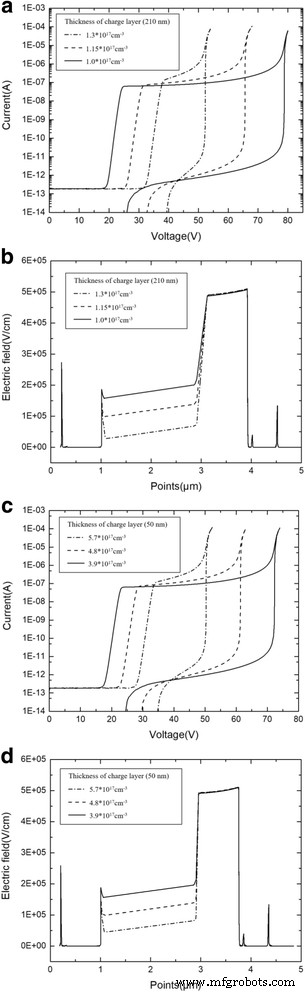
un Photocurrent and dark current with different doping level (thickness of charge layer is 210 nm). Solid line:doping level in the charge layer is 1.3 × 10 17  cm −3 . Dashed line:doping level in charge layer is 1.15 × 10 17  cm −3 . Dashed dot line:doping level in charge layer is 1.0 × 10 17  cm −3 . un Presents the simulation results of currents with different doping level. The device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influence the punch-through voltage, breakdown voltage, and current-voltage characteristic. b Avalanche field with different doping level (thickness of charge layer is 210 nm). Solid line:doping level in charge layer is 1.3 × 10 17  cm −3 . Dashed line:doping level in charge layer is 1.15 × 10 17  cm −3 . Dashed dot line:doping level in charge layer is 1.0 × 10 17  cm −3 . b Presents the simulation results of fields with different doping level. The device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influenced the electric field distribution. c Photocurrent and dark current with different doping level (thickness of charge layer is 50 nm). Solid line:doping level in charge layer is 5.7 × 10 17  cm −3 . Dashed line:doping level in charge layer is 4.8 × 10 17  cm −3 . Dashed dot line:doping level in charge layer is 3.9 × 10 17  cm −3 . c Presents the simulation results of currents with different doping level. The device with a charge layer thickness of 50 nm has a relatively wide and suitable doping level. A minimal change in the doping level has a small influence on the current-voltage characteristic. d Avalanche field with different doping level (thickness of charge layer is 50 nm). Solid line:doping level in charge layer is 5.7 × 10 17  cm −3 . Dashed line:doping level in charge layer is 4.8 × 10 17  cm −3 . Dashed dot line:doping level in charge layer is 3.9 × 10 17  cm −3 . d Presents the simulation results of fields with different doping level. The device with a charge layer thickness of 50 nm only has a relatively wide and suitable doping level. A minimal change in the doping level has a small influence on the electric field distribution

Clearly, the device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influence the current-voltage characteristic and electric field distribution. As a result, the performance of APD varies significantly via several percent deviations of doping concentrations in the thicker charge layer. This conclusion is the same as the theoretical analysis. Concurrently, when designing APD structures, choosing a thin charge layer will give a high level of doping tolerance, as well as confer APD with good controllability.

Finally, the relationship between charge layer and multiplication thickness was simulated. Figure 11a presents the avalanche field with multiplication region thicknesses of 100, 200, and 300 nm in the APD-2 structure (with a charge layer thickness of 70 nm). Figure 11b presents the charge layer doping range with different multiplication thicknesses at the suitable electric field distribution condition. The charge layer thicknesses are 50, 70, and 90 nm. Clearly, a high avalanche field exists in the thin multiplication layer. As the multiplication region thickness decreases, the electric field difference between multiplication and absorption layers increases. As a result, a thin multiplication layer needs a high product of the charge layer doping level and thickness to reduce the high avalanche field.

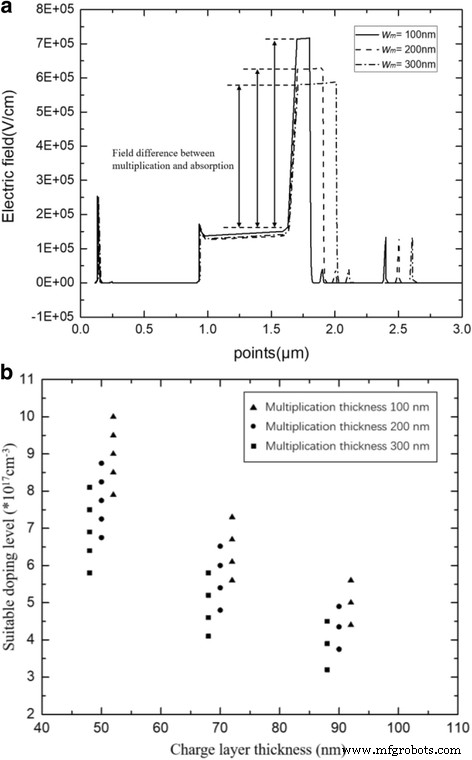
un Avalanche breakdown electric field with different multiplication thicknesses. Solid line:w m  = 100 nm. Dashed line:w m  = 200 nm. Dashed dot line:w m = 300 nm. un Presents the simulation results of electric field distribution with different w m . As the w m decreases, the avalanche field in the multiplication increase. b Relationship between multiplication thickness and charge layer. The thickness of multiplication is 300 nm (black square), 200 nm (black circle), 100 nm (black triangle). b Presents the relationship between multiplication thickness and charge layer. A thin multiplication layer needs a high product of the charge layer doping level and thickness to reduce the high avalanche field

Tunneling Effect on the Electric Field Distribution

The simulation in this part will study the tunneling effect on the electric field in the device. From the theoretical analysis, the tunneling effect has an influence on the avalanche field in multiplication. Thus, the simulation will design to study the influence of electric field in the absorption layer that exceeds the tunneling threshold value. First, group A, with the structure of APD-1, charge layer thickness of 90 nm, and different charge layer doping levels of 1.4 × 10 17 –2.4 × 10 17  cm −3 , was simulated for electric field distribution when the device avalanche breaks down. The result is shown in Fig. 12a. When the charge layer doping level exceeds 2.0 × 10 17  cm −3 , the field in the absorption layer becomes lower than the tunneling threshold field and the avalanche field in the multiplication layer reaches the same value. However, when the doping level is less than 2.0 × 10 17  cm −3 , the field in the absorption layer exceeds the tunneling threshold field and the avalanche field in the multiplication layer decreases with the decrease of the doping level in charge layer. Similar results were observed in the APD-2 structure (with a charge layer thickness of 90 nm and doping level of 2.2 × 10 17 –3.6*10 17  cm −3 ) (Fig. 12b). That is, if the electric field in the absorption layer exceeds the tunneling threshold value at or over the breakdown voltage, then the breakdown electric field in the multiplication will decrease.

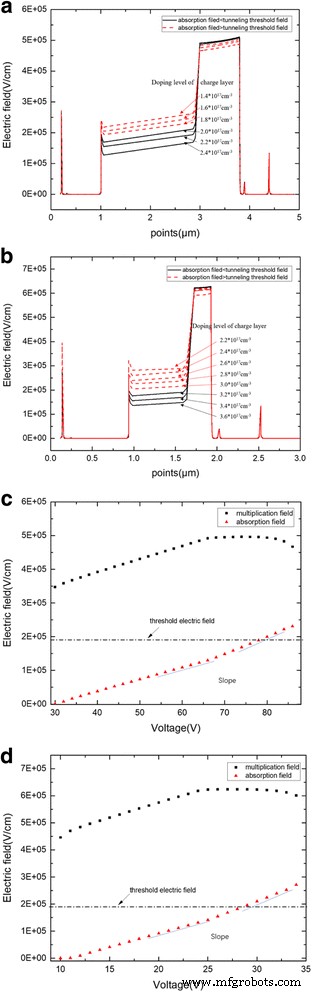
un Avalanche breakdown electric field with different doping levels (APD-1). Thickness of charge layer is 90 nm. Red dashed lines:the field of absorption is larger than the tunneling threshold field. Black solid lines:the field of absorption is less than the tunneling threshold field. un Presents the simulation results of electric field distribution with different doping level while avalanche breakdown. When doping level of charge layer exceeds 2.0 × 10 17  cm −3 , the field in the absorption layer becomes lower than the tunneling threshold field, and the avalanche field in the multiplication layer reaches the same value with different doping level. However, when the doping level is less than 2.0 × 10 17  cm −3 , the field in the absorption layer exceeds the tunneling threshold field, and the avalanche field in the multiplication layer decreases with the decrease of the doping level. Thus, if the electric field in the absorption layer exceeds the tunneling threshold value at or over the breakdown voltage, then the breakdown electric field in the multiplication will decrease. Thus, the electric field in the absorption should be less than the tunneling threshold value to maintain the high field in the multiplication layer when the device avalanche breaks down. b Avalanche breakdown electric field with different doping levels (APD-2). Thickness of charge layer is 90 nm. Red dashed lines:the field of absorption is larger than the tunneling threshold field. Black solid lines:the field of absorption is less than the tunneling threshold field. The figure description of b is similar to a . c Relationship between field and bias voltage in multiplication and absorption (APD-1). Thickness of charge layer is 90 nm. Electric field of multiplication (black square). Electric field of absorption (red triangle). c Presents the relationship between the electric field and bias voltage in multiplication and absorption layers. When the electric field in the absorption layer reaches the tunneling threshold value, the avalanche breakdown electric field in the multiplication gradually decreases. Moreover, the absorption field slope increases when the electric field in the absorption layer exceeds the tunneling threshold. d Relationship between field and bias voltage in multiplication and absorption (APD-2). Thickness of charge layer is 90 nm. Electric field of multiplication (black square). Electric field of absorption (red triangle). The figure legend of d is similar to a

Groups B (APD-1 thickness of 90 nm, doping level of 2.4 × 10 17  cm −3 in charge layer and APD-2 thickness of 90 nm, doping level of 3.6 × 10 17  cm −3 ) were designed to demonstrate the relationship between the threshold electric field in the absorption layer and avalanche field in the multiplication layer. The multiplication and absorption electric fields vary with the bias voltage on the device. As shown in Fig. 12c, d, when the electric field in the absorption layer reaches the tunneling threshold value, the avalanche breakdown electric field in the multiplication gradually decreases. Moreover, when the absorption field exceeds the tunneling threshold, the avalanche breakdown electric field in the multiplication layer plummets. Furthermore, the absorption field slope increases when the electric field in the absorption layer exceeds the tunneling threshold.

The phenomenon in Fig. 12 can be explained by the theoretical analysis that tunneling has an influence on the charge density in the “Methods” section. When the electric field reaches the tunneling threshold value in the absorption layer, the charge density ρ becomes unequal to the dopant ion. The multiplication field will decrease as the negative ion increases, and the absorption field will increase as the positive ion increases. Concurrently, the absorption field slope will increase due to the tunneling effect. As a result, the electric field in the absorption should be less than the tunneling threshold value to maintain the high field in the multiplication layer and the low dark current when the device avalanche breaks down.

Conclusions

In summary, we have presented a theoretical study and numerical simulation analysis involving the InGaAs/InAlAs APD. The mathematical relationship between the device parameters and electric field distribution in the device was built. And the tunneling effect was taken into consideration in the theoretical analysis. Through analysis and simulation, the influence of structure parameters on the device and the detailed relationship of each layer were fully understood in the device. Three important conclusions can be obtained from this paper. First, the doping level and thickness of the charge layer for different multiplication thicknesses can be calculated by the theoretical model in the “Methods” section. Calculated charge layer values (doping and thickness) are in agreement with the experiment results. Second, as the charge layer thickness increases, the suitable doping level range in charge layer decreases. Compared to the thinner charge layer, the performance of APD varies significantly via several percent deviations of doping concentrations in the thicker charge layer. When designing APD structures, choosing a thin charge layer will give a high level of doping tolerance, as well as confer APD with good controllability. Finally, the G btt of tunneling effect was calculated, and the influence of tunneling effect on the avalanche field was analyzed. We confirm that the avalanche field and multiplication factor (M n ) in the multiplication will decrease by the tunneling effect.

Abreviaturas

2D:

Two-dimensional

APD:

Avalanche photodiode

DCR:

Dark count rate

SACM APDs:

Separate absorption, charge, and multiplication avalanche photodiodes

SAGCMAPDs:

Separate absorption, grading, charge, and multiplication avalanche photodiodes

SPAD:

Single-photon avalanche photodiode

SPDE:

Single-photon detection efficiency

SRH:

Shockley–Read–Hall


Nanomateriales

  • Metal
  • Resina
  • fibra
  • Material compuesto
  • Nanomateriales
  • Materiales poliméricos
  • Biologicos
  • Teñir
  • Especias

    1. Tecnologías avanzadas de deposición de capas atómicas para micro-LED y VCSEL
    2. El diseño de la capa de emisión para multiplicadores de electrones
    3. Propiedades fotocatalíticas de los polvos de TiO2 recubiertos con Co3O4 preparados por deposición de capa atómica mejorada con plasma
    4. Investigación teórica de nanocables de germanio tensados ​​biaxialmente por tracción
    5. Ajuste de las morfologías de la superficie y las propiedades de las películas de ZnO mediante el diseño de la capa interfacial
    6. Ajuste de nivel de Fermi de películas de ZnO mediante deposición de capa atómica superciclada
    7. Una investigación sobre una célula solar de silicio cristalino con una capa de silicio negro en la parte posterior
    8. Fotoconductividad entre bandas de puntos cuánticos de InAs / InGaAs metamórficos en la ventana de 1,3 a 1,55 μm
    9. Una simulación teórica de las respuestas a la radiación de la superrejilla de Si, Ge y Si / Ge a la irradiación de baja energía
    10. Crecimiento propio de MOCVD y fotoluminiscencia mejorada espectacularmente de nanocables de núcleo-carcasa de InGaAs / InP
    11. Mecanismos de formación de nanocables de InGaAs producidos por una deposición de vapor químico de dos pasos de fuente sólida