Investigación teórica de nanocables de germanio tensados ​​biaxialmente por tracción

Antecedentes

Como elemento del grupo IV, el germanio (Ge) tiene la superioridad tanto en optoelectrónica como en electrónica y tiene una gran compatibilidad con la fotónica de silicio (Si). Una característica esencial de Ge es que su banda prohibida directa es de alrededor de 0,8 eV (1,55 μ m) a 300 K. La movilidad tanto del electrón como del hueco en Ge es mucho mayor que en Si. Por lo tanto, Ge se ha utilizado en dispositivos de alta velocidad en circuitos integrados actuales basados ​​en Si [1, 2]. Más interesante aún, el Ge tensado por tracción ofrece optimización en los aspectos anteriores. Ge es un semiconductor de banda prohibida indirecta con una ligera diferencia de 136 meV entre L-Valley y Γ -valle [3]. Teóricamente se predice que más del ∼4.0% uniaxial a lo largo de 〈111〉 [4] o ∼1.6–2.0% biaxial [5, 6] de deformación por tracción puede reducir la Γ -valle debajo del valle L, convirtiendo así Ge en un material bandgap directo, lo que abre una nueva ruta para la emisión de luz de los materiales del grupo IV. Otro punto importante es que el Ge tensionado proporciona una mejora significativa en la movilidad del portador [7, 8] para realizar dispositivos semiconductores de óxido metálico complementarios de alta velocidad.

Los nanocables (NW) exhiben atractivas propiedades electrónicas y ópticas debido a la gran relación superficie / volumen y al confinamiento de los portadores y fotones en dos dimensiones (2D) [9]. En los últimos años, los Ge NW (GeNW) en Si [10] o los NW de núcleo / capa Ge / Si [11] se han estudiado exhaustivamente debido a sus potenciales en los transistores de efecto de campo (MOSFET) de semiconductores de óxido metálico para microelectrónica de Si. Tanto la transconductancia escalada como la corriente se mejoraron de tres a cuatro veces en comparación con el Si p convencional -MOSFET [12]. Por tanto, se esperaba que el crecimiento epitaxial de GeNW laterales directamente sobre Si produjera MOSFET de alto rendimiento. Zhang y col. abordó que los GeNW ultrafinos en Si (001) están expuestos con facetas de {105} [13], que tienen la energía superficial predicha más baja [14]. Además, se demostró que el MOSFET de Ge tensado en el sustrato virtual SiGe mejora la movilidad del agujero [1]. Aunque los GeNW laterales en Si con deformación por compresión pueden mostrar una mejora significativa en el transporte de portadores como se supone, no pueden convertirse en una banda prohibida directa. Para introducir deformación por tracción en GeNW, se requieren la aleación GeSn [15] y los compuestos III-Sb [16], que tienen una constante de red mayor que la de Ge. A pesar de que se ha aplicado el método mecánico para fabricar GeNW tensados ​​uniaxialmente [17, 18], el complejo de esta técnica de fabricación apenas puede ser adecuado para la integración monolítica en la electrónica y la fotónica basada en Si. Además, la tensión se liberará fácilmente en los NW independientes, mientras que los GeNW laterales pueden soportar una tensión muy alta por sí mismos. Por lo tanto, se requieren GeNW laterales crecidos epitaxialmente con alta tensión de tracción biaxial para lograr una transición de banda prohibida directa, así como una mejora de la movilidad del portador.

Hasta la fecha, los puntos cuánticos Ge libres de dislocación y altamente sometidos a tensión biaxial en InP (001) han mostrado potencial para la emisión directa de banda prohibida simulada por el método de elementos finitos (FEM) [19]. De manera similar, en este trabajo, teóricamente predecimos la morfología de las superficies expuestas y la dirección de crecimiento de los GeNW sometidos a tensión de tracción biaxial en una plantilla de GaSb relajada que se puede cultivar directamente en Si con una capa tampón de AlSb [16, 20]. Elegimos {110}, {105} y {111} como superficies expuestas de los GeNW laterales y comparamos el cambio de energía total en el sistema de estado estable. Ignoramos la influencia de la dislocación y la fractura [21] en este sistema altamente tenso por simplicidad. La simulación basada en FEM revela que existe una cantidad crítica de Ge. Por debajo del valor crítico, los GeNW están expuestos por {105}, mientras que por encima del valor crítico, están expuestos por {110}. Casi toda la región GeNW se puede convertir en bandgap directo, que es la diferencia de los mínimos de la banda de conducción y los máximos de la banda de orificios de luz en el Γ -punto. Además, también analizamos cualitativamente el cambio de la masa efectiva del portador dependiente de la cepa en el Γ -punto para predecir indirectamente la mejora en la movilidad de los electrones y los huecos.

Métodos

Los NO laterales normalmente revelan una sección transversal en forma de triángulo [22, 23]. Gracias a la propiedad 1D de NW que se muestra en la Fig. 1a, un modelo NW finito similar a Zhang et al. en el material suplementario de Ref. [13] se puede utilizar correctamente para la simulación en la que se fijan las superficies inicial y final que se muestran en la Fig. 1b. Debido al efecto de frontera, solo discutimos la parte central del NO y consideramos que la sección transversal de esta parte representa la situación en un NO infinitivamente largo. El FEM se utiliza para simular la distribución de la deformación por tracción en GeNW con un desajuste de celosía del 7,7% con GaSb. Calculamos el incremento de energía total del sistema después de depositar la misma cantidad de Ge en estado estable en tres situaciones:(i) [100] dirección de crecimiento con {110} facetas expuestas (situación A), (ii) [100] dirección de crecimiento pero con {105} facetas expuestas (situación B), y (iii) [110] dirección de crecimiento con {111} facetas expuestas (situación C). Las secciones transversales de estas tres situaciones se muestran en la Fig. 1c. Las áreas de la sección transversal se mantienen iguales, lo que representa cantidades iguales de Ge.

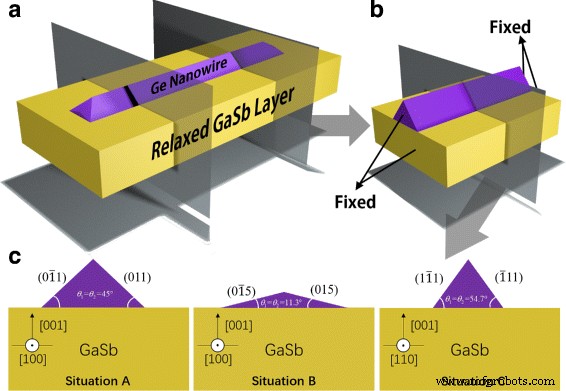
Esquemas de GeNW en GaSb: a Modelo 3D, b modelo finito simplificado y c secciones transversales de GeNW con diferentes facetas

El cambio total de energía del sistema por unidad de longitud (J / nm) incluye la diferencia general en la energía de deformación, la energía de superficie y la energía de borde [24] y puede estar dado por:

$$ \ Delta {{E} _ {\ text {total}}} =\ Delta {{E} _ {\ text {tensión}}} + \ Delta {{E} _ {\ text {superficie}}} + \ Delta {{E} _ {\ text {edge}}}. $$ (1)

El primer término Δ E _{s t r a yo n} representa la diferencia de energía de deformación del sistema estable antes y después de la deposición de Ge y se expresa en volumen unitario,

$$ \ Delta {u} =\ frac {1} {2 {Y}} \ sum \ limits_ {i =j} ^ {{}} {\ tau_ {ij} ^ {2}} - \ frac {\ nu } {Y} \ sum \ limits_ {i donde τ _ij = C _ij ε _ij ( i, j =1, 2, 3) denota el tensor de tensión, C _ij y ε _ij son las constantes elásticas y el tensor de deformación, respectivamente, Y y G son el módulo de Young equivalente y el módulo de corte equivalente, respectivamente, y ν es la razón de Poisson equivalente. En la sección transversal 2D considerada, el cambio total de energía de deformación se puede obtener integrando el área con el valor de Δ u en cada punto. El segundo término Δ E _{s u r f a c e} está relacionado con la diferencia de energía superficial antes y después de la deposición de Ge. La energía superficial en la sección transversal de nuestras situaciones se puede reescribir como [23]

$$ {{\ gamma} _ {i}} =\ frac {2h} {\ sin {{\ theta} _ {i}}} ({{\ sigma} _ {i}} - {{\ sigma} _ {{(001)}}} \ cos {{\ theta} _ {i}}) $$ (3)

donde h es la altura de la sección transversal GeNW, σ _i ( yo =A, B y C) es la energía superficial promedio de las facetas expuestas debajo del área de la unidad, y el ángel correspondiente entre las facetas NW y la interfaz está etiquetado con θ _i como se muestra esquemáticamente en la Fig. 1c. La deformación en energía superficial puede despreciarse debido a su leve impacto como el tratamiento en Ref. [25]. La Tabla 1 muestra los valores de energía superficial de la literatura. El último término llamado cambio de energía de borde representa el cambio en el costo de energía para formar bordes afilados y viene dado por

$$ \ Delta {{E} _ {\ text {edge}}} =3 \ varGamma $$ (4)

donde 3Γ es la energía de borde total que contiene las intersecciones de la faceta superior y dos basales. El valor estimado de 3Γ es 3,7 eV / nm por ajuste experimental [26] y la influencia de la energía del borde puede ignorarse debido al valor apenas variado [25]. Por tanto, es válido calcular el incremento de energía de Δ E _total −3Γ.

Después de conocer la distribución de la deformación, la banda de conducción dependiente de la deformación disminuye en Γ - y el L-valle se puede calcular despreciando el efecto cuántico. La banda de conducción del Γ -el valle se baja solo con tensión hidrostática por

$$ \ Delta E_ {c} ^ {\ Gamma} ={{a} _ {c}} ({{\ varepsilon} _ {xx}} + {{\ varepsilon} _ {yy}} + {{\ varepsilon } _ {zz}}) $$ (5)

donde a _c denota potencial de deformación hidrostática con el valor de −8,24 eV en el Γ -punto [27], ε _xx , ε _yy y ε _zz son la cepa en x , años, y z dirección en el sistema de coordenadas del material, respectivamente. Sin embargo, el desplazamiento de la banda de conducción en el punto L está sujeto a deformaciones tanto hidrostáticas como de cizallamiento [19], dado por

$$ {{} \ begin {alineado} \ Delta {E_ {c} ^ {\ mathrm {L}}} =&\ left ({{\ Xi} _ {d}} + \ frac {1} {3} {{\ Xi} _ {u}} \ right) ({{\ varepsilon} _ {xx}} + {{\ varepsilon} _ {yy}} + {{\ varepsilon} _ {zz}}) \\ &- \ frac {2} {3} {{\ Xi} _ {u}} \ left (| {{\ varepsilon} _ {xy}} | + | {{\ varepsilon} _ {yz}} | + | { {\ varepsilon} _ {xz}} | \ derecha) \ end {alineado}} $$ (6)

donde Ξ _d y Ξ _u son el potencial de deformación por dilatación con el valor de −6,97 eV y el potencial de deformación uniaxial con el valor de 16,3 eV en el L-valle, respectivamente. Para convertir Ge en un material bandgap directo, el Γ -valle tiene que ser más bajo que el L-valle, lo que significa \ (\ Delta {E_ {c} ^ {\ Gamma, \ text {L}}} =\ Delta E_ {c} ^ {\ Gamma} - \ Delta {E_ {c} ^ {\ mathrm {L}}} <- 0,136 \) eV. Aquí, usamos \ (\ Delta {E _ {\ text {DT}}} =\ Delta E_ {c} ^ {\ Gamma, \ text {L}} + 0.136 \) para presentar la diferencia en el Γ - y el punto L. Una vez que Γ -punto desciende por debajo del punto L, Δ E _DT será negativo. Se simula una serie de GeNW sometidos a tensión de tracción con tamaños variados para mostrar la transición de banda prohibida directa.

Además, debido a la alta tensión de tracción en el GeNW, el Γ -valle está por debajo del L-valle mientras que el máximo de la banda de agujeros de luz se convierte en el máximo de valencia [28]. La banda prohibida en un GeNW de tan alta tensión será la diferencia entre el Γ -valle y los máximos de banda de agujeros de luz en el Γ -punto. Por lo tanto, la banda prohibida distribuida espacialmente, así como las energías del borde de la banda en el Γ -punto que es k =0, incluida la banda de conducción, la banda de orificios pesados ​​y la banda de orificios ligeros, se calculan mediante k.p de ocho bandas teoría [29]. Ignoramos el efecto cuántico ya que es muy débil en nuestro modelo GeNW con un ancho basal de 40 nm. El resultado se puede aplicar para estudiar la recombinación de agujeros de electrones en el GeNW tensado por tracción, así como el mecanismo de mejora de la movilidad. Generalmente, la movilidad del electrón o del hueco puede estar dada por μ = e τ / m ^∗ , donde m ^∗ es la masa efectiva del portador y τ es el tiempo de dispersión electrón-fonón. En el modelo de una aproximación parabólica para el Γ - y L-valles con dispersión isotrópica, el tiempo de dispersión es proporcional a \ (m_ {DOS} ^ {* - 3/2} \), lo que lleva a la conclusión de que la relación de movilidad alcanza μ _Γ / μ _L =182 si el Γ -valley se mueve por debajo del L-valle y tanto el tiempo de dispersión electrón-fonón como la masa efectiva de electrones son invariables con la deformación [30]. Sin embargo, teniendo en cuenta la complejidad en el cálculo de la dispersión anisotrópica y la masa efectiva dependiente de la deformación en nuestro modelo de NW, solo analizamos cualitativamente la mejora en la movilidad de los electrones y los huecos en un GeNW de alta tensión a través de la disminución de ambos electrones. y masa efectiva del agujero en el Γ -punto.

Resultados y discusiones

Consideramos que el sistema está inicialmente bajo tensión de tracción total debido al gran desajuste de celosía del 7,7% entre Ge y GaSb. La Figura 2 muestra la distribución de la deformación residual 2D, incluida la deformación en el plano ε _xx , deformación cortante ε _xy y deformación vertical ε _zz de la situación A con el ancho base de w =40 nm, por ejemplo, en estado estable después de la relajación. La definición de cepa aquí es ( a _Ges - a _Ge ) / a _Ge , donde a _Ges y a _Ge son constantes de celosía de Ge tensado y relajado, respectivamente. Como se ve en la Fig. 2a, ε _xx tiene el valor máximo de aproximadamente 15,4% en dos bordes basales que es mucho mayor que la deformación inicial, pero disminuye bruscamente desde el borde hacia el centro con el valor mínimo de aproximadamente 3,3%. En z -dirección desde la parte inferior hasta la parte superior de GeNW, ε _xx también cae debido a la relajación de GeNW. La distribución de ε _zz tiene características similares con ε _xx en la Fig. 2b. A diferencia de la deformación biaxial en la película delgada de Ge, la Fig. 2c muestra que el componente de deformación por cizallamiento distribuido asimétricamente de GeNW juega un papel importante en la transición de banda prohibida directa. La distribución de la tensión es bastante similar en tres situaciones. Sin embargo, los valores de los componentes de deformación son diferentes en tres situaciones debido a la diversa relación ancho-alto ( W / H ) inducida por su forma. La situación B con GeNW expuesta por {105} superficies tiene la W más grande / H de 10, exhibiendo una alta tensión similar a la de la película delgada de Ge. La situación C con {111} superficies expuestas también muestra una alta deformación, ya que la orientación de crecimiento NW a lo largo de [110] sigue siendo un valor invariable de deformación, lo que eleva el valor de ε _xx y ε _yy simultaneamente. Por lo tanto, la tensión en el plano difícilmente se puede relajar.

Distribución de la deformación residual de un GeNW en la situación A con un ancho basal de 40 nm: a x deformación del componente ε _xx , b deformación del componente z ε _zz y c deformación cortante en el plano x-y ε _xy . La forma de zigzag en la parte inferior denota la capa de sustrato parcial (lo siguiente tiene el mismo significado)

De acuerdo con la distribución de la deformación, se puede obtener el incremento de la energía de deformación. Como se discutió anteriormente, la situación B tiene el incremento de energía de deformación más alto, mientras que la situación A tiene el más bajo. Sin embargo, para el cambio de energía superficial, la situación B da valores negativos decrecientes al aumentar el área de la sección transversal y las otras dos situaciones revelan valores positivos muy cercanos en la misma área. El incremento de energía total excluyendo el cambio de energía de borde se muestra en la Fig. 3a. El resultado muestra que es menos probable que se formen GeNW solo en la situación C debido a que el incremento de energía nunca es el más bajo. Hay dos consecuencias diferentes del incremento de energía con el aumento del área, y la línea de trazos vertical está marcada para presentar el valor crítico del área, A _c =136.2nm ² , que significa las cantidades de Ge. Cuando el área es inferior a 136,2 nm ² , Los GeNW tienden a formar la forma en la situación B, pero en la situación A después de depositar más Ge. El resultado del cálculo predice que los GeNW sometidos a tensión de tracción en GaSb pueden preferir formar altos W / H forma de triángulo en la sección transversal cuando se deposita una cantidad baja de Ge, mientras que se forma un W bajo / H uno después de exceder el valor crítico. La Figura 3b-e muestra las distribuciones de la deformación hidrostática y la suma del valor absoluto de los componentes de la deformación por cortante en las situaciones A y B bajo el área crítica. Comparando la situación A con B, a pesar de que la situación A tiene el mayor valor máximo tanto de la deformación hidrostática como de | ε _xy | + | ε _yz | + | ε _xz |, la situación B tiene una deformación hidrostática promedio mayor pero un valor promedio menor de | ε _xy | + | ε _yz | + | ε _xz |. Mientras tanto, la situación B demuestra una pequeña diferencia en la distribución espacial de la deformación hidrostática y | ε _xy | + | ε _yz | + | ε _xz |. Estas propiedades son muy similares a las de la película fina Ge y se atribuyen a su alto W / H valor. Como resultado, refiriéndose a las Ecs. (5) y (6), la situación B presenta un valor menor de Δ E _DT que el de la situación A, lo que conduce a una alta posibilidad de convertir Ge en un material bandgap directo.

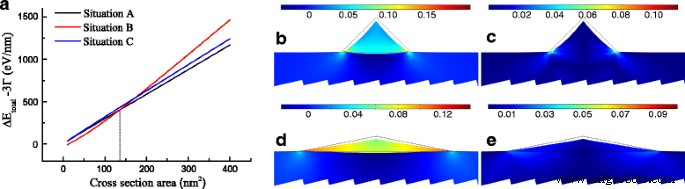
un El cambio de energía total excluyendo el cambio de energía de borde 3 Γ frente al área de la sección transversal (la línea discontinua es el valor crítico de un mínimo de aproximadamente 136,2 nm ² en diferentes situaciones). b - e deformación hidrostática y | ε _xy | + | ε _yz | + | ε _xz | en b , c situación A y d , e situación B en el valor crítico

Debido a la alta tensión de tracción en GeNW, casi toda la región de GeNW se puede convertir en banda prohibida directa. La figura 4a muestra la distribución de Δ E _DT con el aumento del tamaño de GeNW. El valor de Δ E _DT cae de arriba a abajo en GeNWs. Curiosamente, el mínimo de Δ E _DT se encuentra en el borde inferior de la sección transversal en la situación B, pero en el centro inferior en la situación A. La razón de esta distribución diferente es que la deformación cortante significativa en el borde inferior en la situación A contribuye más a \ (\ Delta E_ {c} ^ {\ mathrm {L}} \) que en la situación B. Para GeNW en la situación B por debajo del área crítica, el promedio Δ E _DT es mucho más bajo que en la situación A por encima del área crítica como se muestra en la Fig. 4b. En el punto crítico, el promedio de Δ E _DT sube repentinamente del valor de −0,308 a −0,137 eV. Además, para la misma forma, la distribución y el promedio de Δ E _DT son básicamente similares, sin una relación obvia con el tamaño. Para descubrir la relación inherente a la deformación en GeNW, graficamos el componente de deformación hidrostática en la base de GeNW con ancho basal en la Fig. 5. Las curvas del componente de deformación hidrostática con diferentes tamaños versus la posición relativa de la base en una GeNW casi se superponen excepto por la diferencia en la región periférica. Las consecuencias consistentes se encuentran en ε _xx y la suma de los componentes absolutos de corte. Por lo tanto, el valor inducido por deformación de Δ E _DT posee la distribución idéntica en GeNW con la misma forma.

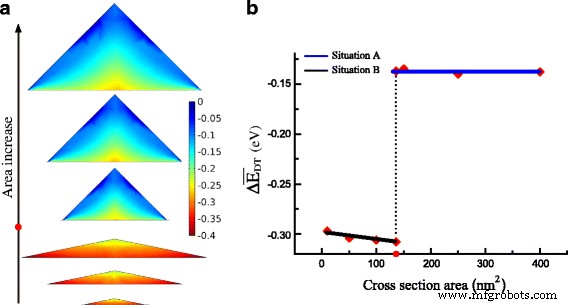
un La distribución de Δ E _DT con aumento del área (la barra de color denota el valor de Δ E _DT ). b El promedio de Δ E _DT vs. el área. El valor crítico está marcado con punto rojo en el eje del área

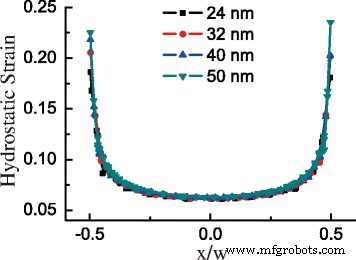
Componente de deformación hidrostática en la base de GeNW frente a x / w con diferentes anchos basales

Además, simulamos el mapeo de banda prohibida inducida por deformación en la sección transversal del GeNW de 40 nm de ancho que se muestra en la Fig. 6a. La distribución espacial de la banda prohibida se deriva del valor variable de los bordes de la banda dependientes de la deformación en el Γ -punto. La Figura 6b muestra la energía del borde de la banda en Γ -punto a lo largo de la z -dirección del GeNW. Encontramos que tanto la banda de conducción como los bordes de la banda de valencia, incluida la banda del agujero ligero y la banda del agujero pesado, cambian significativamente en los primeros 15 nm y luego ligeramente. Las partes superiores de la banda de orificios ligera y pesada se separan y tienden a desplazarse en direcciones opuestas al aumentar la tensión de tracción. De la Fig. 6a, b, la banda prohibida aumenta significativamente en los primeros 15 nm para alcanzar aproximadamente 0,30 eV, luego cambia ligeramente alrededor de un valor de 0,24 eV, que es la banda prohibida en la mayoría de las regiones GeNW. Dado que el máximo de la banda del agujero ligero es más alto que el de la banda del agujero pesado en el Γ -punto en el GeNW, los agujeros en la banda de valencia prefieren situarse en los máximos de la banda de agujeros de luz. Por lo tanto, la recombinación de huecos de electrones ocurrirá entre el mínimo de la banda de conducción y el máximo de la banda de huecos de luz en el Γ -punto si descuidamos la superposición de las funciones de onda de hueco y electrón dependientes del espacio. Curiosamente, los máximos de la banda de orificios de luz se mueven incluso por encima de los mínimos de la banda de conducción en la región del fondo NW marcado como una curva negra en la Fig. 6a con una deformación hidrostática superior a ∼5.0%. La banda prohibida negativa que calculamos bajo una deformación de alta tensión puede tener consecuencias complicadas, como una estructura de banda semimetálica [31] o invertida [32].

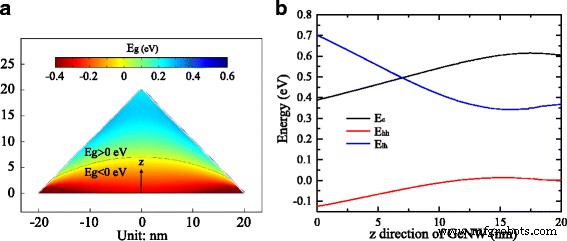
un Bandgap dependiente de la deformación en el GeNW distribuido por posiciones. b Las energías del borde de la banda dependientes de la deformación a lo largo de z dirección en el GeNW

Por último, la movilidad de los electrones y los huecos se mejorará bajo una tensión de tensión tan alta en el GeNW. Para Ge relajado, el transporte de electrones es aportado principalmente por electrones domiciliados en el L-valle. Cuando Ge está bajo tensión de tracción de modo que Γ -valle está debajo del L-valle como se muestra en la Fig. 3a, la contribución principal del transporte de electrones es de la Γ -Valle. Por otro lado, la participación dominante de los huecos en el transporte proviene de la banda de huecos de luz en el Γ -punto bajo tensión de alta tensión, mientras que la banda del agujero pesado ocupa los máximos de la banda de valencia en el caso relajado. Debido a una masa efectiva de electrones mucho más pequeña en el Γ -punto que el del punto L, así como la disminución de la masa efectiva desde los máximos de la banda de agujeros pesados ​​hasta los máximos de la banda de agujeros ligeros, se puede mejorar la movilidad no solo de los electrones sino también de los agujeros. Teóricamente se puede predecir que la deformación por tracción reducirá la masa efectiva de electrones y huecos en el Γ -punto en un modelo de punto cuántico de Califano y Harrison [29]. Aunque el método de cálculo cuantitativo no es adecuado para nuestro modelo NW, asumimos cualitativamente que la deformación por tracción puede modificar la masa efectiva a k =0 aumentando la curvatura de la relación de dispersión para k pequeños en las cercanías del Γ -punto. Por lo tanto, la movilidad tanto de los electrones como de los huecos se puede mejorar en los GeNW sometidos a tensión de tracción. La división de las bandas de valencia también induce un fuerte acoplamiento electrón-fonón y dispersión intrabanda [33], lo que limita la movilidad del hueco para que sea menor que la movilidad de los electrones.

Conclusiones

En resumen, hemos propuesto GeNW tensados ​​por tracción en GaSb, comparando tres situaciones diferentes a través del cambio de energía total antes y después de la deposición de Ge. El resultado muestra que el GeNW está inclinado a formar {105} superficies a lo largo de la dirección de crecimiento 〈100〉 antes de la cantidad crítica, mientras que está expuesto por {110} superficies después de la cantidad crítica. El campo de deformación residual y el análisis de banda prohibida han demostrado que la misma forma tiene una distribución similar tanto en deformación como en Δ E _DT independientemente del tamaño. Además, la deformación en el plano y la deformación hidrostática se reducen no solo desde los bordes hacia el centro, sino también desde la parte inferior hacia la parte superior en todas las situaciones. Debido a la alta tensión de tracción, casi todo el GeNW en GaSb se puede convertir en un material de banda prohibida directa en las dos situaciones posibles. Además, los agujeros de luz participan principalmente en la recombinación de los agujeros de electrones y el transporte eléctrico en el Γ -punto porque los máximos de la banda de agujeros de luz se convierten en los máximos de la banda de valencia en una deformación de alta tensión. La movilidad no solo de los electrones sino también de los huecos se puede mejorar debido a la disminución de la masa efectiva del portador en el Γ -punto determinado por la deformación por tracción. El atractivo rendimiento predicho teóricamente implica que los GeNW sometidos a tensión de tracción prometen ser aplicados a la optoelectrónica para fuentes de luz y a la microelectrónica para dispositivos de alta velocidad en Si-fotónica y electrónica, respectivamente.

Propiedades de las oscilaciones electromagnéticas longitudinales en metales y su excitación en superficies planas y esféricas Propiedades eléctricas de materiales compuestos con alineación asistida por campo eléctrico de rellenos de nanocarbono