Propiedades eléctricas de materiales compuestos con alineación asistida por campo eléctrico de rellenos de nanocarbono

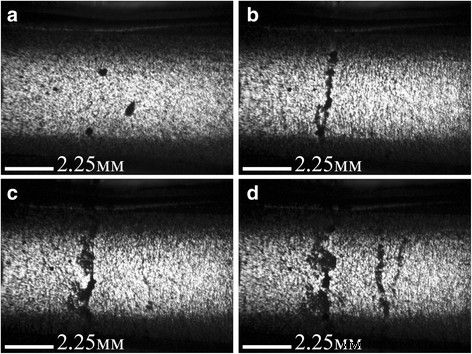
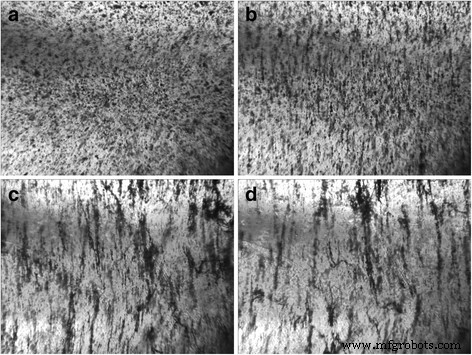
Imágenes ópticas de 0,05% en peso de GNP / Larit 285 compuesto bajo la acción del campo eléctrico de CA (frecuencia de 15 kHz, fuerza de 167 kV / m) (en condensador): а— antes de la acción del campo eléctrico; b —Después de 12 min; c —Después de 26 min; d —Después de 60 min de acción de campo eléctrico. Tamaño de imagen 10,8 × 8,0 mm ²

Imágenes ópticas de 0,05% en peso de compuestos MWCNT / Larit 285 bajo la acción del campo eléctrico de CA (frecuencia de 15 kHz, intensidad de 83,3 kV / m) (electrodos integrados): a - antes de la acción del campo eléctrico; b - después de 12 min; c - después de 26 min; d - después de 60 min de acción de campo eléctrico. Tamaño de imagen 10,8 × 8,0 mm ² [26]

Imágenes ópticas de 0,05% en peso de compuestos MWCNT / Larit 285 bajo la acción del campo eléctrico de CA (frecuencia de 15 kHz, intensidad de 50 kV / m) (electrodos integrados): а —Antes de la acción del campo eléctrico; b —Después de 12 min; c —Después de 26 min; d —Después de 60 min de acción de campo eléctrico. Tamaño de imagen 10,8 × 8,0 mm ² [26]

Procesados ​​con campo eléctrico de CA, los compuestos se volvieron más transparentes con el aumento del tiempo de acción del campo eléctrico debido al movimiento del relleno en la dirección de las líneas eléctricas de un campo eléctrico externo. También se observó que con el aumento del tiempo de acción del campo eléctrico, las estructuras alineadas del relleno de carbón se ensanchan y surgen algunos espacios libres entre ellas. Esto puede deberse a las interacciones de Van der Waals de nanopartículas de carbono. De esta manera, las cadenas de relleno de nanocarbono de distribución especificada se forman en el material compuesto.

Como se ve en la Fig.1, para los compuestos GNP / Larit 285 en configuración de electrodos embebidos, la acción del campo eléctrico de CA se manifiesta en la creación de la ruta conductora principal, que cierra el suministro con electrodos de voltaje externos y conduce a un flujo de corriente de alta amplitud a través del muestra compuesta. Por lo tanto, la alineación de los GNP en Larit 285 fue realizada por el conjunto experimental cuando el compuesto se coloca entre las placas del condensador. La Figura 2 muestra que tal configuración de configuración experimental en la que el flujo de corriente a través de la muestra es imposible, permite obtener cadenas de GNP alineadas consistentemente en una matriz de polímero.

En el caso del tratamiento de compuestos MWCNTs / Larit 285 con campo eléctrico de CA, también se observó una formación de alargamiento en la dirección de las cadenas de campo eléctrico. Las cadenas distintas se vuelven más gruesas cuando aumenta el tiempo de exposición al campo de CA. Pero el tiempo característico de formación de cadenas alineadas en MWCNT / compuesto epoxi es de minutos, mientras que en GNP / compuesto epoxi es de segundos en la configuración de electrodos incrustados. Además, debido a la forma y el tamaño de GNP, la distribución alineada del relleno en los compuestos de GNP / epoxi se puede formar con menos magnitudes de campo eléctrico de CA que en los compuestos de MWCNT / epoxi. Pero, por otro lado, debido a la movilidad de los GNP debido a su forma y tamaño en comparación con los MWCNT, la formación de compuestos a granel con relleno de GNP es complicada. La red alineada de PNB tiende a destruirse poco después de apagar el campo eléctrico si el compuesto no se ha polimerizado por completo.

Al considerar todas las imágenes ópticas de la red alineada bajo formación de campo eléctrico de CA en GNP / - y MWCNT / compuestos epoxi, podemos concluir que en igualdad de condiciones cuando se cambia solo el tipo de relleno de carbón, la red alineada se forma más rápido en los GNP / epoxi compuesto. En el caso de los MWCNT, su tendencia a la aglomeración impide una alineación eficaz en la dirección del campo eléctrico aplicado. Cabe señalar que el campo DC no es eficaz para la formación de una red alineada en material compuesto [26].

Para explicar la observación por microscopía óptica de las peculiaridades de la alineación asistida por campo eléctrico del relleno de diferente morfología, se estimó teóricamente un tiempo característico de rotación de las nanopartículas de carbono en la matriz epoxi bajo la acción del campo eléctrico de CA.

Modelado de la alineación de partículas de carbono en medio viscoso

El mecanismo del compuesto con una distribución espacial específica del método de formación de relleno es que cada nanopartícula de carbono que está incrustada en la matriz dieléctrica se polariza bajo la acción del campo eléctrico de CA debido a la polarización de la interfaz entre el polímero y la partícula. Generalmente, el momento de polarización y el vector de campo eléctrico no son colineales debido a la anisotropía de las nanopartículas. Por lo tanto, cuando se activa el campo eléctrico, se produce un par que conduce a la rotación de las nanopartículas de carbono en la dirección del campo. Se sabe que el movimiento de rotación de una partícula en este caso se describe mediante la siguiente ecuación [16]:

donde yo es el momento de inercia de la nanopartícula de carbono; Θ es el ángulo entre la partícula y la dirección del campo eléctrico; T _η es un par de amortiguación; \ ({T} _ {\ mathrm {align}} \ approx \ left [\ overrightarrow {\ mu} \ times \ overrightarrow {E} \ right] \) es el par inducido por el campo; \ (\ overrightarrow {\ mu} =f \ left (\ varepsilon, {\ sigma} _1, {\ sigma} _2, v \ right) \) es el momento de polarización que depende de los valores de la constante dieléctrica ( ε ) y conductividad ( σ ₁ , σ ₂ ) de nanopartículas y matriz; v = f ( m , l , d ) es el volumen de nanopartículas de carbono que depende de su peso ( m ) y dimensiones ( l , d ).

Generalmente, el momento de polarización \ (\ overrightarrow {\ mu} \) es proporcional al campo externo \ (\ overrightarrow {E} \) y al volumen de la partícula ν y está determinado por la fórmula [28]:

donde ε ₀ es la permitividad del espacio libre, ε _m es una constante dieléctrica de la matriz, β es un parámetro adimensional que, en particular, depende de la forma de inclusión. En [28], fórmulas de β para un disco y cilindro conductores ideales se dan:

De estas dependencias se deduce que \ ({\ overrightarrow {\ mu}} _ {II} \ ne {\ overrightarrow {\ mu}} _ {\ perp} \) ( II significa codirección del eje largo de la partícula y de la dirección del campo, ⊥ — perpendicularidad). Por lo tanto, para GNP y MWCNT, \ ({\ overrightarrow {\ mu}} _ {II}> {\ overrightarrow {\ mu}} _ {\ perp} \) debido a su forma y propiedades.

Evaluar el tiempo característico de rotación de las partículas de carbono bajo la acción de un campo eléctrico y su alineación por la dirección del campo Eq. (1) con las condiciones iniciales Θ ( t =0) = Θ ₀ , \ (\ frac {d \ varTheta} {dt} \ left (t =0 \ right) =0 \) fueron resueltos. Según [16], los términos de la ecuación principal de movimiento son los siguientes:

donde \ ({\ alpha} ^ {\ ast} =\ left ({\ left ({\ varepsilon} _p ^ {\ ast} - {\ varepsilon} _m ^ {\ ast} \ right)} ^ 2 \ right) / \ left (\ left [{\ varepsilon} _m ^ {\ ast} + \ left ({\ varepsilon} _p ^ {\ ast} - {\ varepsilon} _m ^ {\ ast} \ right) {L} _x \ right] \ left ({\ varepsilon} _p ^ {\ ast} + {\ varepsilon} _m ^ {\ ast} \ right) \ right) \) es una polarización, \ ({\ varepsilon} _ {m, p} ^ {\ ast} ={\ varepsilon} _ {m, p} -j \ frac {\ sigma_ {m, p}} {\ omega} \) y ε _{m , p} , σ _{m , p} son la constante dieléctrica y la conductividad del medio y la partícula, ω =2 πf , f —Frecuencia de campo eléctrico.

Para determinar el factor de despolarización de nanotubos de carbono y nanoplaquetas de grafito, deben considerarse como partículas de cierta forma (Fig. 5). MWCNT solo se puede considerar como elipsoide. La elipticidad del MWCNT en aproximación elipsoide es \ (e =\ sqrt {1 - {\ left (2 {r} _0 / l \ right)} ^ 2} \). El GNP se puede considerar como esferoide o como elipsoide. La elipticidad del GNP en aproximación elipsoide es \ (e =\ sqrt {1 - {\ left (h / 2R \ right)} ^ 2} \) y en aproximación esferoide es \ (e =\ left (2R / h \ derecha) \ sqrt {1 - {\ left (h / 2R \ right)} ^ 2} \). Entonces, las expresiones del factor de despolarización toman la siguiente forma [28].

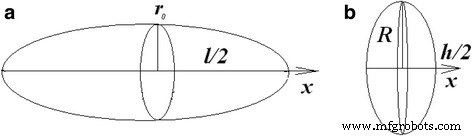
Imágenes esquemáticas de nanotubos de carbono ( a ) y nanoplaquetas de grafito ( b )

Para el elipsoide:

$$ {L} _x =\ frac {1- {e} ^ 2} {e ^ 3} \ left (Arth \ kern0.5em e-e \ right). $$

Para el esferoide:

$$ {L} _x =\ frac {1+ {e} ^ 2} {e ^ 3} \ left (e- \ arctan \ kern0.5em e \ right), \ kern2.5em {L} _x + 2 { L} _R =1. $$

En las ecuaciones anteriores, L _x es un factor de despolarización si el campo externo se aplica a lo largo de la x -eje (como en la Fig. 5), L _R es un factor de despolarización si el campo externo se aplica a lo largo del radio de PNB.

Gastando los factores de despolarización en serie, las expresiones anteriores toman la siguiente forma.

Para el MWCNT elipsoidal:

$$ {L} _x =\ frac {4 {r} _0 ^ 2} {l ^ 2} \ left [\ ln \ left (\ frac {l} {r_0} \ right) -1 \ right] $$ ( 2)

Para el GNP elipsoidal:

$$ {L} _x =\ frac {h ^ 2} {4 {R} ^ 2} \ left [\ ln \ left (\ frac {4R} {h} \ right) -1 \ right] $$ (3 )

Para GNP esférico:

$$ {L} _x \ approx 1- \ frac {h \ left (8 \ pi {R} ^ 2-16hR + 3 \ pi {h} ^ 2 \ right)} {32 {R} ^ 3} $$ (4) $$ {L} _R \ approx \ frac {h \ left (8 \ pi {R} ^ 2-16hR + 3 \ pi {h} ^ 2 \ right)} {64 {R} ^ 3} $ $ (5)

Además, para resaltar las peculiaridades de la morfología de las partículas, se preguntó el volumen de CNT como el volumen de un cilindro hueco \ (\ nu =\ pi l \ left ({r} _0 ^ 2- {r} _i ^ 2 \ right) \ ), mientras que el volumen GNP se solicitó como el volumen de un disco ν = πR ² h .

El momento de inercia de los nanotubos de carbono se tomó como \ (I =\ frac {ml ^ 2} {12} \):el momento de inercia de una varilla recta delgada con la longitud de l y masa de m , el eje de rotación es perpendicular a la varilla y pasa por su centro de masa. El momento de inercia de las nanoplaquetas de grafito se tomó como \ (I =\ frac {mR ^ 2} {2} \) - el momento de inercia del disco, cuyo radio es R y masa de m , el disco gira alrededor de la perpendicular a su eje plano.

Luego, utilizando todo el enfoque anterior y estableciendo parámetros numéricos, se llevaron a cabo los cálculos del cambio del ángulo de inclinación de partículas de diferente morfología en relación con la dirección del campo con el tiempo de tratamiento del campo eléctrico de CA.

Basado en papel [29] donde las dependencias experimentales de concentración de partes reales y complejas de permitividad dieléctrica de los compuestos con grafito fino y nanotubos de carbono fueron descritas por la fórmula y ecuaciones de Nielsen.

$$ {\ varepsilon} _ {CNT} ^ {\ ast} =62.2 \ hbox {-} 12.4 \ times i, \ kern1em {\ varepsilon} _c ^ {\ ast} =34.3 \ hbox {-} 13.4 \ veces i $$

se dan, en nuestros cálculos para el PNB ε _{p ( PNB )} =34,3, y para MWCNT, ε _{p ( CNT )} =62.2 fue tomado.

Los parámetros geométricos de las partículas se tomaron de la Tabla 1. Con respecto a otros parámetros numéricos utilizados, se indicó que ε ₀ =8,85 × 10 ⁻¹² F / m, η =0,75 Pa × s, f =15 kHz, ε _m =2.8 ε ₀ [30], σ _m =10 ⁻⁶ Sm / m [16]. La conductividad de las partículas de carbono individuales se tomó como σ _{p ( CNT )} =10 ⁵ Sm / m [31], σ _{p ( PNB )} =10 ⁵ Sm / m [32, 33] _.

La Figura 6 muestra el ángulo de inclinación de la partícula con respecto a la dirección del campo aplicado, la dependencia del tiempo de acción del campo cuando L _x fue evaluado por las Ecs. (2) y (3). Los resultados se encontraron para dos valores de intensidad de campo:1 kV / m (Fig.6a) y 36 kV / m (Fig.6b) suponiendo que la partícula está casi completamente desordenada en el momento inicial ( Θ ( t =0) = π /2.05).

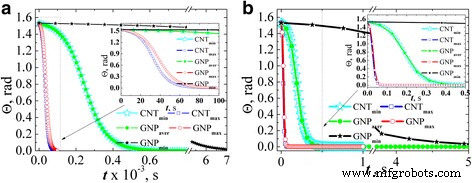
La evolución del ángulo de inclinación de las partículas de relleno de carbono con respecto a la dirección del campo estimada en elipsoides Aproximación para una intensidad de campo eléctrico de CA de 1 kV / m ( a ) y 36 kV / m ( b )

Ha habido una clara correlación entre la relación de aspecto de las partículas y el tiempo de alineación por el campo eléctrico. Es decir, el tiempo máximo para la alineación es para las partículas con la relación de aspecto más baja (GNP _min ). Para GNP _max y CNT _max , el tiempo de alineación es casi igual, y el mismo tiempo de alineación es para GNP _aver y CNT _min .

La Figura 7 muestra los valores del factor de despolarización estimados por las Ecs. (2) y (3) para PNB y MWCNT. L _x es un factor geométrico y no depende de los valores absolutos de los semiejes de los elipsoides simulados, sino de su relación. Por lo tanto, L _x es una función directa de la relación de aspecto de las partículas.

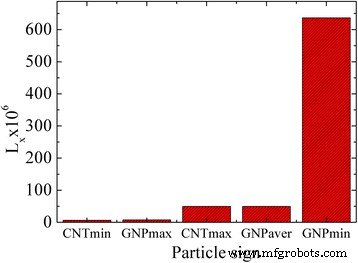
Factor de despolarización para PNB y MWCNT evaluados por Ecs. (2) y (3)

Es decir, el factor de despolarización es el principal parámetro del problema. Dado que su expresión depende de la morfología y el tamaño de la partícula, el tiempo característico de rotación de los GNP y MWCNT difiere.

El contenido de la Figura 8 es análogo al de la Figura 6, dependencias del ángulo de inclinación de los PNB en relación con la dirección del campo aplicado en el tiempo de acción del campo cuando L _R fue evaluado por Eq. (5). Los resultados se encontraron para dos valores de intensidad de campo:1 kV / m (Fig.8a) y 36 kV / m (Fig.8b) suponiendo que las partículas están casi completamente desordenadas en el momento inicial ( Θ ( t =0) = π /2.05). A modo de comparación, los resultados de los cálculos de la dependencia del ángulo para MWCNT ( L _x fue evaluado por Eq. (2)) se introducen en los mismos gráficos.

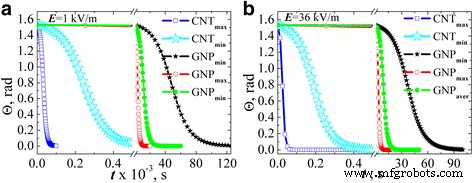
La evolución del ángulo de inclinación de las partículas de relleno de carbono con respecto a la dirección del campo estimada en aproximación de elipsoides para MWCNT y en aproximación de esferoide para GNP a una intensidad de campo eléctrico de CA de 1 kV / m ( a ) y 36 kV / m ( b )

La Figura 9 muestra las dependencias del ángulo de inclinación de los GNP en relación con la dirección del campo aplicado en el tiempo de acción del campo en una aproximación a que el GNP es un esferoide con factor de despolarización (4). La evaluación se realizó para la intensidad del campo eléctrico de CA 1 kV / m (Fig. 9a) y 36 kV / m (Fig. 9b) suponiendo que en el momento inicial la partícula está aproximadamente desordenada ( Θ ( t =0) = π /2.05).

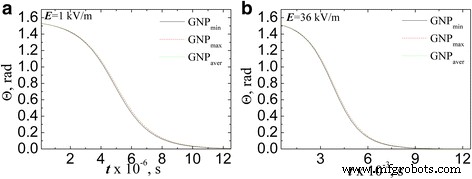
La evolución del ángulo de inclinación de los PNB en relación con la dirección del campo estimada en aproximación esferoide ( L _x fue tomada por la Eq. (4)) a una intensidad de campo eléctrico de CA de 1 kV / m ( a ) y 36 kV / m ( b )

A partir del análisis presentado en los datos de la Fig.9, se extrajeron las siguientes conclusiones:en primer lugar, si asumimos que el eje del campo eléctrico está codirigido con el x -eje de GNP, el tiempo de rotación aumenta significativamente en comparación con el cálculo en el caso del eje de campo y codirección del radio de GNP. Y este comportamiento es independiente de la relación de aspecto de los PNB. En segundo lugar, el curso de la dependencia es mínimamente diferente para las partículas con diferentes relaciones de aspecto, y en un cierto punto del tiempo de proceso, la partícula más alineada es la partícula con una relación de aspecto mínima GNP _min mientras que GNP _aver y GNP _max los ángulos coinciden. Este comportamiento se debe al valor del factor despolarizante que es cercano a 1 para los casos anteriores.

Por lo tanto, la estimación ha demostrado que el tiempo de rotación de las partículas de carbono bajo la acción del campo eléctrico de CA depende de su morfología y relación de aspecto. Tenga en cuenta que el modelo considera una partícula incrustada en la matriz de polímero, mientras que en el compuesto, tenemos un conjunto de partículas con diferentes ángulos de inclinación iniciales. Esa es una de las razones por las que el tiempo característico real de toda la formación de la red puede ser muy diferente del tiempo estimado.

Además, es complicado lograr tal distribución de MWCNT en una mezcla compuesta donde cada tubo individual está enredado. Se sabe que los nanotubos de carbono tienden a enredarse debido a la interacción de sus superficies. Por lo tanto, el tiempo real de los MWCNT en la alineación de mezcla compuesta es significativamente más alto de lo que se estimó teóricamente. Además, la viscosidad de la mezcla compuesta con el mismo contenido de MWCNT es más alta que la viscosidad de la mezcla compuesta con GNP. Todos estos factores impiden una alineación tan rápida de MWCNT en compuestos como se estimó.

Propiedades eléctricas de compuestos sólidos

Dentro del estudio, se encontraron experimentalmente valores de resistividad de los compuestos GNPs / Larit 285 preparados con distribución de relleno alineada y aleatoria en matriz epoxi. La Figura 10 presenta las dependencias de concentración de la conductividad eléctrica de los compuestos GNP / Larit 285 con distribución de relleno alineada y aleatoria. Las propiedades eléctricas de las muestras compuestas se investigaron longitudinalmente y perpendicularmente a las aplicadas en la dirección del campo eléctrico de fabricación compuesta. La Figura 11 presenta las dependencias de concentración de la conductividad para compuestos MWCNT / Larit 285 (а) [27] y GNP / Larit 285 (b) en una escala logarítmica.

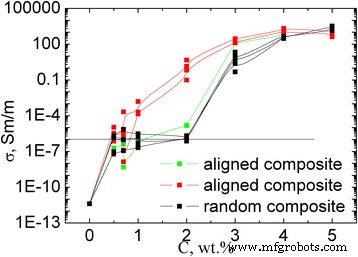
Dependencia de la concentración de la conductividad eléctrica de los compuestos GNP / Larit 285 con distribución de relleno alineada y aleatoria en escala logarítmica

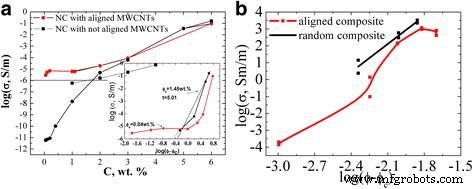
Dependencia de la concentración de la conductividad de MWCNTs / Larit 285 ( a ) [27] y PNB / Larit 285 ( b ) en escala logarítmica

Los valores más bajos de la conductividad σ corresponden a las muestras de resina epoxi sin relleno (conductividad de 10 ⁻¹¹ Sm / m). Con los PNB que se suman al compuesto, su conductividad aumenta y alcanza el valor de σ =10 ⁻⁶ Sm/m (this value is considered as percolation level) at GNPs content с in composite of φ _с =2 wt% for the composites with random filler distribution. For the GNPs/Larit 285 composites with aligned filler distribution, percolation concentration is of φ _с =0.84 wt%. Thus, materials of the identical composition are characterized by different values of percolation threshold depending on the method of preparation and filler distribution in the polymer matrix (aligned or random).

Conductivity of GNPs/Larit 285 composites smoothly increases with the increment of GNPs content for both types of the samples while the shape of the dependence is completely different for the MWCNTs/Larit 285 composites obtained by the same method [27] (see Fig. 11). Concentration dependence of conductivity of MWCNTs/Larit 285 composites increases with the increment of MWCNTs content at low filler content until it reaches a plateau, then conductivity increases again. Such a difference of conductivity concentration dependence can be explained by another process of conductive network formation if the fillers are of different morphology. MWCNTs/epoxy composites are characterized by crossed framework structure formation while in GNPs/epoxy composites chained structure appears. GNPs addition to the polymer matrix smoothly increases the number of conductive links in composite. In case of entangled by themselves frame MWCNTs, there is an area where nanotubes addition to the matrix has little effect on its conductivity.

Statistical percolation model operates with probabilities of particles in composite to create a conductive chain at their certain content. As it was shown in our paper, manufactured with electric field treatment, composites become conductive at lower content of carbon filler due to activation of dynamic percolation which is a phenomenon when conductive chain formation is stimulated by external influences at such a content of conductive particles in composite which is not enough for statistical percolation.

It should be noted that the existence of two types of percolation transitions is a characteristic feature of composite materials which are in low-viscosity state during the manufacture [34]. The higher value of percolation concentration cannot be changed by varying the manufacturing conditions of the composite since it is defined by statistical percolation theory. Statistical percolation threshold is defined by the filler type, its aspect ratio, surface state of polymer and filler, wettability, uniformity of filler distribution, and its content in polymer matrix. As we have shown, dynamical percolation threshold can be shifted by activating of filler particle movement in polymer matrix, by electric field action, and, thus, promoting a conductive network formation. The value of dynamic percolation threshold can be changed with method of composite manufacture change. We have established that in case of filler alignment under electric field action, dynamical percolation threshold is defined not only by the above parameters but also by parameters of the applied field and polymer matrix viscosity, filler morphology.

Conclusions

1. 1.

   Nanocarbon-polymer composite material with aligned distribution of graphite nanoparticles in epoxy matrix has been produced by exposing to a high-voltage AC electric field. The influence of electric field treatment time, strength, and configuration of electric field on formation of aligned GNPs network in liquid polymer medium was investigated by optical microscopy.

2. 2.

   It was shown that the influence of AC electric field at composite fabrication process leads to the manifestation of two types of percolation transitions:statistical and dynamic ones. In addition, the aspect ratio of the filler particles and the character of the formation of the conducting cluster, depending on the shape of the particles, determine the shape of the σ =f(c) dependence and the critical concentration of both dynamic and statistical percolation thresholds.

3. 3.

   The effects of the morphology of the filler particles on the process of nanocarbon alignment in polymer matrix under AC electric field have been investigated by estimating of carbon nanotube and graphite nanoplatelet rotation time using an analytical model based on effective medium approach. The theoretical evaluation of characteristic time of carbon nanoparticle of different morphology rotation under AC electric field action have shown that rotation time of carbon nanoparticle is determined by its depolarization factor which in turn depends directly on the aspect ratio of particle.

4. 4.

   The investigation of concentration dependences of conductivity of composites GNPs/Larit 285 with aligned by AC electric field action filler distribution and random filler distribution in epoxy matrix have shown that under AC electric field action composites, percolation threshold decreases essentially from ϕ _c =2 wt% for composites with random filler distribution of GNPs to ϕ _c =0.84 wt% for the obtained under AC electric field action GNPs/Larit 285 composites.

Abreviaturas

AC:

Alternative current

AFM:

Microscopía de fuerza atómica

CNTs:

Carbon nanotubes

DC:

Direct current

GNPs:

Graphite nanoplatelets

MWCNTs:

Multiwall carbon nanotubes

SEM:

Microscopía electrónica de barrido

Investigación teórica de nanocables de germanio tensados ​​biaxialmente por tracción Fabricación de alto rendimiento de nanofibras de calidad utilizando un electrohilado de superficie libre modificado