Las propiedades eléctricas de los compuestos híbridos basados ​​en nanotubos de carbono de paredes múltiples con nanoplaquetas de grafito

Métodos

Materiales

La Figura 1a presenta una imagen SEM de nanotubos de carbono de paredes múltiples usados ​​(MWCNT) con una pureza ≥90% (Cheap Tubes Ins.). La imagen de microscopía óptica de los GNP que se utilizó como segundo relleno se muestra en la Fig. 1b.

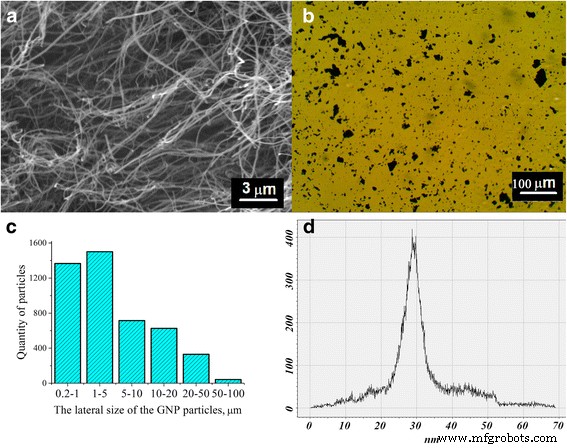
Imágenes SEM para MWCNT ( a ). Imagen óptica para el GNP ( b ). Las distribuciones de partículas (diagrama) en el tamaño lateral de TEG después de 30 h de dispersión ultrasónica en agua (GNP) ( c ). Histogramas de distribución de espesores de PNB obtenidos en medios dispersivos, en agua ( d )

El grafito expandido térmicamente (TEG) es un producto del grafito disperso natural ( d =50–300 μm, h =5–30 μm) intercalación con H ₂ SO ₄ y posterior tratamiento térmico en un horno con flujo ascendente de acuerdo con el método desarrollado y se informó en un artículo publicado anteriormente [22]. La peculiaridad del proceso de ultrasonidos de TEG en el medio de agua es que las partículas de TEG no se hunden sino que flotan en la superficie. Por esta razón, la exfoliación de TEG en GNP es complicada. Después de 30 h de ultrasonidos con TEG en el medio acuoso, la mayor parte de los GNP tienen un diámetro de 0,2 a 5 μm; sin embargo, también se producen partículas grandes de 10 a 100 μm de diámetro (Fig. 1c).

Sobre la base de imágenes AFM convertidas en 3D de GNP obtenidas en diferentes medios dispersivos, llevamos a cabo un análisis comparativo de los espesores de GNP. Los histogramas de distribución de espesores se presentan en la Fig. 1d. Según los resultados de AFM, la variación de la distribución del espesor para los PNB (obtenidos en medio de agua) fue de 5-55 nm con el máximo de distribución a 28 nm. La estimación de las dimensiones laterales permitió calcular la relación de aspecto de los PNB, que es de ~ 40-900 para los PNB. Por tanto, se puede concluir que los PNB obtenidos en medio dispersivo de agua poseen la amplia distribución de espesores y dimensiones laterales. Sin duda, esto es favorable para una mayor conductividad eléctrica del material compuesto con el relleno de este tipo.

Las características estructurales y morfológicas de las cargas investigadas se presentan en la Tabla 1. Como puede verse en la Tabla 1 y la Fig. 1, la forma de una carga de nanocarbono difiere considerablemente. Por lo tanto, los GNP se pueden considerar como discos y los MWCNT como cilindros.

Preparación de materiales compuestos

Este artículo presenta los resultados de la investigación de los cambios de resistividad eléctrica y conductividad térmica de compuestos de polímeros híbridos con nanotubos de carbono de paredes múltiples (MWCNT) tras la adición de una cantidad constante del segundo relleno en forma de disco eléctricamente conductor:nanoplaquetas de grafito.

Para el estudio de las propiedades eléctricas de los compuestos poliméricos de resina de carbono-epoxi, se han preparado dos sistemas:

• ➢Sistema de dos componentes, donde se utilizaron GNP o MWCNT de paredes múltiples como rellenos: materiales monocompuestos (MCM)

• ➢Sistema de tres componentes, donde se utilizó GNP de relleno eléctricamente conductor como segundo relleno para CM con MWCNT: materiales compuestos híbridos (MCH)

Materiales compuestos mono

Durante nuestro trabajo, sintetizamos e investigamos los sistemas compuestos basados ​​en epoxi Larit 285 (Lange Ritter GmbH, Alemania). Esta resina tiene las siguientes características:epoxi equivalente =165-170, número de epoxi:0,59 ÷ 0,65.

Para preparar MCM de nanocarbono / epoxi, se incorporaron rellenos de nanocarbono en la resina epoxi Larit 285 (viscosidad de 600 a 900 mPa s) con H285 (viscosidad:50 ÷ 100 mPa s, índice de amina:480 ÷ 550 mgKOH / g) como un agente endurecedor. El contenido del relleno de nanocarbono en los MCM varió de 0,03 a 4% en volumen.

El polvo de GNP se sometió a tratamiento con UV / ozono (para CM mono e híbridos). El tratamiento con UV / ozono se realizó utilizando una lámpara DRT-1000. Los polvos de GNP iniciales se sometieron a un tratamiento con UV / ozono durante 20 minutos [22, 23].

Se colocaron tres gramos de epoxi Larit 285 en el tubo de ensayo para su posterior disolución en el disolvente de acetona. Se pesó nanocarbono en forma de polvo para la concentración seleccionada y se agregó a la solución de epoxi-acetona. El relleno de nanocarbono (GNP o MWCNT) se mezcló mecánicamente con resina epoxi y acetona. Se agitó una mezcla de estos componentes durante 30 min (para GNP) o 60 min (para MWCNT) en un baño ultrasónico para una distribución más uniforme del relleno en el polímero, luego se añadió el agente de curado H285 y se vertió una mezcla en moldes y curados a temperatura ambiente durante 48 a 72 h para completar la polimerización.

Materiales compuestos híbridos

Los MWCNT se utilizaron para la preparación de HCM, como relleno electroconductor principal con concentraciones variables de 0,03 a 4% en volumen. Para estudiar las propiedades sinérgicas del relleno eléctrico disperso adicional, se agregaron PNB a los sistemas dados en un contenido de 0,24% en volumen.

Los MWCNT se mezclaron con resina epoxi y acetona. Se agitó una mezcla de estos componentes durante 60 min en un baño ultrasónico para una distribución más uniforme de la carga en el polímero. Luego, se añadió polvo de GNP y se mezcló completamente mecánicamente, y todo se agitó durante 30 min en un baño ultrasónico. Luego, se agregó el agente de curado H285 y se vertió una mezcla en moldes y se curó a temperatura ambiente durante 48 a 72 h para completar la polimerización.

Para las medidas de conductividad eléctrica, las muestras con forma de paralelepípedo rectangular con un tamaño de 3,5 × 3,5 × 10 mm ³ estaban preparados. El rango de conductividad de medición fue de 10 ⁻¹² a 10 S / m.

Métodos de prueba

La dispersión ultrasónica del polvo de TEG se llevó a cabo en un baño ultrasónico "BAKU" BK-9050, frecuencia estadounidense:40 kHz, con una potencia de salida máxima de 30 y 50 W. Las dimensiones laterales de los GNP preparados se investigaron mediante el uso de un microscopio óptico. MIKMED-1 con la cámara digital ETREK DCM-510 adjunta y sonda NanoLaboratory INTEGRA. Para estimar el grosor y el diámetro promedio de los GNP, sus imágenes de microscopio óptico y de fuerza atómica (AFM) se convirtieron en imágenes 3D mediante el programa Nova, que creó los histogramas de distribución de densidad del GNP.

El tratamiento con UV / ozono se realizó utilizando DRT-1000 (lámpara ultravioleta) equipada con lámpara de arco de descarga eléctrica de alta presión inflada con mercurio y compuesto de argón que podría liberar radiación ultravioleta de 50 W a una longitud de onda de 240-320 nm. La distancia entre la lámpara UV y la muestra se fijó en 11 cm.

La resistencia eléctrica de las muestras se midió con dos sondas ( R =10 ⁴ –10 ⁹ Ω) y cuatro sondas ( R ≤ 10 ⁴ Ω) o mediante el teraohmímetro E6-13 ( R =10 ⁹ –10 ¹³ Ω). Se utilizó una instalación automatizada para la investigación de la resistencia eléctrica en el rango de temperatura de 6 a 300 K. Los componentes principales de la instalación automatizada fueron una varilla para una muestra, una dirección de corriente de conmutación de potencia y una fuente de voltaje estable, un análogo –Convertidor digital ADC 16-32F (SDI), una computadora personal y los cables de interfaz. La temperatura se midió con un termopar de cobre-constantano ubicado cerca de la muestra. El rango de medición de la resistencia eléctrica (0.01–10 ¹⁴ Ω) se dividió en varias regiones:0,01–2,5 Ω, donde el error no supera el 0,5%; 2.5–10 ⁷ Ω (el error fue <1%); R =10 ⁸ Ω (<5%); R =10 ⁹ Ω (<10%); R =10 ¹⁰ –10 ¹³ Ω (<20%). Al medir la resistencia eléctrica de los CM, se probaron tres muestras para cada concentración.

Resultados y discusión

Conductividad eléctrica de los compuestos poliméricos con rellenos mono e híbridos

El umbral de percolación ϕ _cr se investigó utilizando medidas de conductividad volumétrica. La dependencia de la conductividad volumétrica eléctrica de los compuestos preparados del contenido de relleno se muestra en la Fig. 2. Los valores para las concentraciones más bajas corresponden a la conductividad de la resina epoxi pura de 7,9 × 10 ⁻¹² ° S / m.

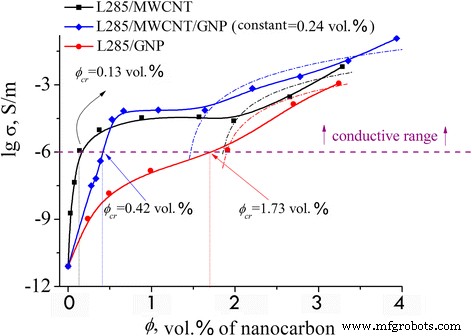
Conductividad eléctrica de compuestos en función del contenido de nanocarbonos. Línea continua las curvas experimentales; línea de puntos las curvas calculadas según Eq. (1)

Como puede verse en la Fig. 2, las dependencias de concentración de la conductividad tanto para MCM como para HCM tienen dos transiciones de percolación. El más bajo (al 0,13% en volumen) se encontró para las muestras con MWCNT. A partir de 0,137% en volumen de MWCNT, los valores de conductividad son superiores a 10 ⁻⁶ S / m que representa el rango conductivo. Para muestras basadas en PNB, la concentración crítica más alta ϕ _cr es igual a 1,7% en volumen y solo hay una transición de percolación por encima del valor de conductividad de 10 ⁻⁶ S / m. Para muestras con cargas mixtas con concentración constante de PNB ( ϕ =0,24% en volumen), se encontró que la concentración crítica de MWCNT / GNP era igual ϕ _cr =0,42% vol y se sitúa entre los valores de los composites con cargas puras.

Comportamiento similar de σ ( ϕ ), es decir, se observó la presencia de dos transiciones de percolación en la curva de concentración para varios compuestos [24,25,26,27].

Josef Z. Kovacs y otros [24] consideran que tales umbrales de percolación inducidos por procesos cinéticos y, por lo tanto, no pueden determinarse utilizando la ley común de escalado de percolación de la teoría de percolación estadística.

Además, Mamunya y otros han obtenido la transición de doble percolación en [25]. Los autores también utilizaron los compuestos polímero-nanotubos de carbono, pero combinaron dos polímeros (copoliamida y polipropileno) como una matriz polimérica, que mezclaron con el relleno a altas temperaturas (125, 167 ° C) y prensaron a 180 ° C.

Suponemos que la existencia de dos umbrales de percolación en nuestro trabajo es un rasgo característico de los materiales compuestos que tienen una baja viscosidad en la etapa de fabricación de la muestra (Fig. 2 y Tabla 2).

Creemos que la primera transición de percolación se puede considerar como una transición de percolación cuasi-dinámica por analogía con la transición de percolación dinámica observada en los compuestos polímero-carbono, donde la transición de percolación se forma bajo la acción de fuerzas externas (campo eléctrico o magnético, presión , etc.) [24, 27].

En la región de baja concentración, después de la adición de endurecedor, el polímero líquido con nanocarbono tiene una viscosidad baja. Las partículas del relleno de carbono en la matriz polimérica se pueden representar como aglomerados suficientemente grandes de nanopartículas (incluso a pesar de la dispersión ultrasónica de larga duración) y nanopartículas separadas (nanotubos o GNP) con una movilidad suficientemente alta en una matriz polimérica de baja viscosidad. Bajo la acción de van der Waals o fuerzas electrostáticas, estas nanopartículas separadas (nanotubos) pueden moverse conectándose entre sí, así como con grandes aglomerados de nanopartículas. Por lo tanto, debido a este desplazamiento, hasta que la matriz del polímero se endurece, estas nanopartículas móviles por separado pueden formar cadenas conductoras que proporcionan la conductividad de toda la muestra.

La formación de la "plataforma" o meseta después del umbral de percolación cuasi-dinámico en dependencia de la concentración de la conductividad eléctrica para CM con MWCNT y relleno híbrido (donde domina la concentración de CNT) depende de varios factores. Está principalmente relacionado con el aumento de la concentración de relleno, que conduce a una mejora de la viscosidad de la muestra sin curar y al movimiento restringido de las partículas separadas para formar nuevas cadenas conductoras. En segundo lugar, también aumenta el número de partículas móviles separadas. Además, el aumento simultáneo de la viscosidad y el número de nanopartículas individuales capaces de mover eficientemente desacelera el proceso de formación de las cadenas conductoras y, en consecuencia, el crecimiento de la conductividad al aumentar la concentración de relleno. Se ve en la Fig. 2 que para lograr la segunda concentración crítica, se requiere agregar una cantidad significativa de relleno a CM. Luego, las partículas individuales inician la interacción entre sí, así como los aglomerados de partículas y los aglomerados de partículas con un solo CNT.

La transición de percolación cuasi-dinámica no se puede describir en el marco de la teoría clásica de percolación (Fig. 3a). La segunda transición de percolación está definida y descrita por la teoría estadística de percolación (Fig. 3b – d) [28, 29]:

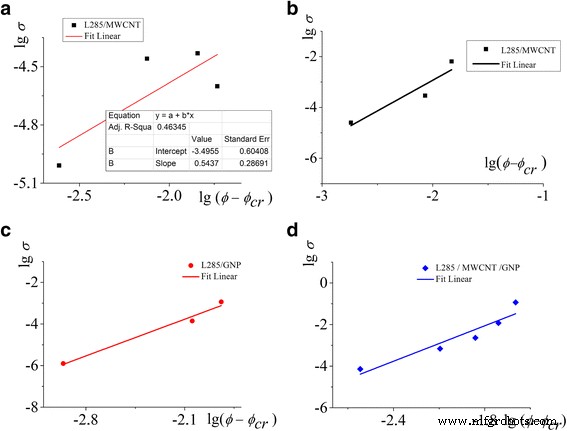
un - d Dependencia de escala (lg σ en función de lg (ϕ - ϕ _cr )) para determinar los parámetros de la Ec. (1). un La transición de percolación cuasi-dinámica, b , c , d La teoría estadística de la percolación

$$ \ sigma \ left (\ phi \ right) \ sim B {\ left (\ phi - {\ phi} _ {\ mathrm {cr}} \ right)} ^ t $$ (1)

donde ϕ _cr es la concentración crítica (umbral de percolación), t es el índice crítico y B es la constante de proporcionalidad en el modelo de percolación clásico. Las constantes B , ϕ _cr y t se ajustaron utilizando el método de minimización del error cuadrático medio (Fig. 3, Tabla 2). Los valores ajustados de ϕ _cr se incluyen en la Fig. 2.

En la Fig. 4, presentamos la conductividad eléctrica versus la concentración para MCM – L285 / MWCNT y HCM – L285 / MWCNT / GNP. Como se puede ver en la imagen, la transición de percolación es la misma para ambos compuestos. Se observa un efecto sinérgico como una mejora de la conductividad eléctrica de HCM por encima de la concentración crítica (Fig. 4). El mayor efecto sinérgico se observó en CM con la combinación de dos rellenos eléctricamente conductores, nanotubos de carbono y nanoplaquetas de grafito, y a una concentración de 2% en volumen, la conductividad eléctrica es 20 veces mayor y en 4% en volumen, 10 veces mayor en comparación con MCM. .

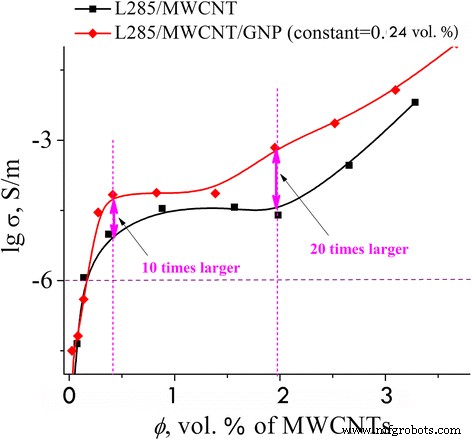
Conductividad eléctrica de materiales compuestos en función del contenido de MWCNT

Para comprender el mecanismo de formación de cadenas conductoras en el CM híbrido donde se observa un efecto sinérgico, ilustramos el posible esquema en la Fig. 5. Para desenredar los haces de CNT, se someten a dispersión ultrasónica. Como resultado, no todos los CNT se desenredan, además de que se rompen reduciendo su relación de aspecto; por lo tanto, aumenta el número de CNT necesarios para la formación de las cadenas conductoras.

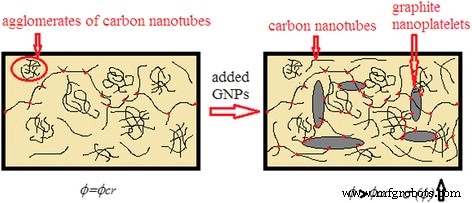
Principios de formación de vías conductoras en híbridos CM-L285 / MWCNT / GNP

Para lograr un efecto sinérgico, concebimos agregar una pequeña cantidad de partículas de GNP en un compuesto con CNT para la conexión de aglomerados de CNT no completamente desenredados. Debido al medio líquido (es decir, una resina de baja viscosidad) y una percolación cuasi-dinámica, no pudimos alcanzar el umbral de percolación más bajo que en el mono CM con CNT. Podemos explicarlo solo por el hecho de que en el caso de la transición de percolación ultrabaja (0,13% en volumen), las cadenas conductoras continuas no se forman en grandes cantidades (se ve en la Fig.4, ya que los valores de conductividad son bajos en la primera transición de percolación) principalmente de partículas de CNT separadas, que no están agrupadas y aún no tienen contacto con las partículas de GNP. Después del umbral de percolación, se observa un aumento significativo de la conductividad del CM híbrido debido a las cadenas adicionales de aglomerados de CNT y GNP (Fig. 5).

Las características morfológicas del componente conductor de nanocarbono del relleno son de importancia crítica durante la formación de cadenas conductoras. La cantidad total de cadenas (por lo tanto, la resistencia al contacto entre las partículas y las características de percolación) en el CM se ve afectada principalmente por la forma del relleno (forma de esqueleto de CNT y forma de cadena de GNP). Para investigar el número de cadenas y la resistencia de contacto entre las partículas en el CM, utilizamos un modelo de la resistencia eléctrica efectiva.

En términos del modelo propuesto, la resistencia eléctrica de la cadena consistió en partículas de nanocarbono que son las siguientes [30]:

$$ {R} _ {\ mathrm {CM} \ _ \ mathrm {G} \ mathrm {N} \ mathrm {P} \ left (\ mathrm {MWCNT} \ right)} =\ frac {N _ {\ mathrm { GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {in} \ _ \ mathrm {cadena}}} {N _ {\ mathrm {cadena} \ _ \ mathrm {in} \ _ \ mathrm {C } \ mathrm {M}} ^ {*}} \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) $$ ( 2)

donde \ ({N} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {in} \ _ \ mathrm {cadena}} =\ frac {b \ left (1 \ kern0 .5em \ mathrm {cm} \ right) \ cdot \ gamma} {l} =\ frac {\ gamma} {l} \) es la cantidad de partículas de nanocarbono en una cadena, b es la longitud de la muestra (1 cm), γ es el factor constante con valor de 1 a 2, l es la longitud de la partícula de nanocarbono (GNP o CNT), r _{GNP (MWCNT)} es la resistencia eléctrica de la partícula de relleno (para las partículas en forma de disco - \ ({r} _ {GNP (disco)} ={\ rho} _ {GNP} \ cdot \ frac {d} {d \ cdot h} =\ frac {\ rho_ {GNP}} {\ mathrm {h}} \), para el cilíndrico - \ ({r} _ {\ mathrm {MWCNT} \ left (\ mathrm {cilindro} \ right)} ={\ rho} _ {\ mathrm {MWCNT}} \ cdot \ frac {4 l} {\ pi {d} ^ 2} \)), h es el grosor de la partícula de nanocarbono, d es el diámetro y R _к es la resistencia eléctrica del contacto único entre las partículas del relleno (CNT o GNP).

En resumen, la resistencia eléctrica del polímero / nanocarbono CM se puede evaluar como [30]:

$$ {R} _ {\ mathrm {CM} \ _ \ mathrm {G} \ mathrm {N} \ mathrm {P} \ left (\ mathrm {MWCNT} \ right)} =\ frac {N _ {\ mathrm { GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {in} \ _ \ mathrm {cadena}}} {N _ {\ mathrm {cadena} \ _ \ mathrm {in} \ _ \ mathrm {C } \ mathrm {M}} ^ {*}} \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) =\ frac {\ gamma ^ 2 \ pi \ cdot z} {4 F} {\ left (\ frac {F - {\ phi} _ {\ mathrm {cr}}} {\ phi - {\ phi} _ {\ mathrm { cr}}} \ right)} ^ t \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) $$ (3)

donde N ^* _{cadena_en_CM} es el número de cadenas de nanocarbono conectadas en paralelo. Este número es proporcional a la cantidad total de partículas que participan en la electroconducción. F es el factor de empaque ( F =0.05 para PNB y F =0.06 para CNT), z = h es para GNP y \ (z =\ frac {d ^ 2} {l} \) es para CNT. Este modelo tiene en cuenta no solo la concentración crítica ϕ _cr , factor de empaque F y resistividad eléctrica del relleno r _{GNP (MWCNT)} sino también la morfología de las partículas (relación de aspecto).

En términos del modelo propuesto, se calcularon los valores siguientes:dependencia de la concentración de la conductividad eléctrica σ _dc ( ϕ ), contacte la resistencia eléctrica R _к y número de cadenas ininterrumpidas N ^* _{cadena_en_CM} (ver Fig. 6, Tabla 3).

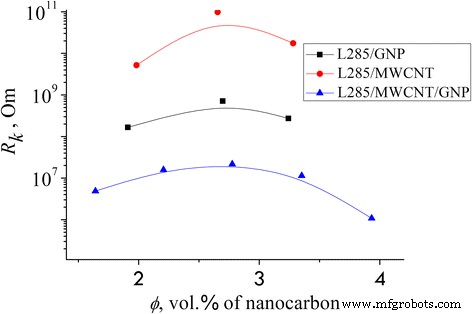
Resistencia de contacto R _k de los CM estudiados, que se calculó mediante la ecuación. (3)

Como podemos ver en la Tabla 3, el valor de la resistencia eléctrica de contacto R _к muestra un mínimo de 10 ⁺⁶ –10 ⁺⁷ Ω para relleno híbrido y máximo cerca de 10 ⁺⁹ –10 ⁺¹⁰ Ω para CM basado en CNT. Los CM basados ​​en CNT tienen una cantidad total de cadenas ininterrumpidas 300 (600) veces mayor N ^* _{cadena_en_CM} que los CM basados ​​en GNP (relleno híbrido) con concentración 2,70% en volumen. La conductividad eléctrica de L285 / MWCNT / GNP es más alta que la conductividad eléctrica de un CM binario (Fig. 2).

Por otro lado, la formación de la red conductora de partículas de nanocarbono no necesariamente provocaría una alta conductividad eléctrica. Según [31], las simulaciones numéricas mostraron que la resistencia de contacto entre diferentes nanotubos varía de 100 kOhm a 3,4 MOhm y depende en gran medida de la estructura atómica de la superficie de contacto y la relajación estructural de las partículas. La resistencia de contacto puede aparecer durante la formación de la capa dieléctrica entre los puntos de contacto de los componentes de relleno (debido al mojado). Esta capa dieléctrica degrada la conductividad y estimula la formación de túneles de los portadores de carga [32].

Resistencia eléctrica R _к entre dos partículas en contacto se puede evaluar de la siguiente manera [33]:

$$ {R} _ {k \ left (\ mathrm {tunel} \ right)} =\ frac {V} {w \ cdot j} =\ frac {h ^ 2 \ delta} {w {e} ^ 2 \ sqrt {2 m \ lambda}} \ exp \ left (\ frac {4 \ pi \ delta} {h} \ sqrt {2 m \ lambda} \ right) $$ (4)

donde δ es el espesor de la capa de polímero; j es la densidad de la corriente del túnel; V es la diferencia de potencial; e y m son la carga y la masa de un electrón, respectivamente; h es la constante de Planck; λ es la altura de la barrera [34,35,36] (en el caso del epoxi λ ≈ 1 eV [33]); y w es el valor de túnel transversal.

La Figura 7 muestra que los valores de la resistencia de contacto eléctrico en el caso del mecanismo de tunelización de la conductividad dependen de la distancia (espesor de la capa de polímero) entre las partículas de relleno para una variedad de valores de tunelización de la sección transversal (calculados usando la expresión 4) .

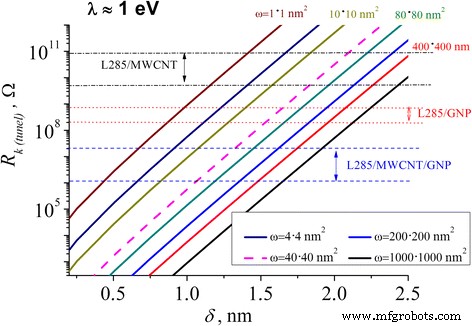
Las dependencias de la resistencia de contacto del espesor de la capa de polímero entre las partículas de relleno para varios valores de la tunelización transversal w

La Figura 7 demuestra la fuerte dependencia de la R _{k (túnel)} en δ . Por lo tanto, al aumentar δ valores de 0,5 a 2,5 nm, R _{k (túnel)} el valor creció en nueve órdenes de magnitud independientemente de la sección transversal del túnel w .

Las simulaciones numéricas mostraron que la distancia entre las partículas de GNP se degrada lentamente de 1,63 a 1,53 nm para el w =40 × 40 nm ² , que atestigua la ausencia de tunelización y destrucción de la cadena conductora para δ ≤ 1,63 nm.

En el caso de los CM basados ​​en CNT, la disminución de δ de 1,83 a 1,57 nm con w =10 × 10 nm ² es causado por los tamaños más pequeños de CNT en comparación con los tamaños de GNP. Suponemos que δ of GNP-based CM is smaller due to the ultraviolet treatment (cleaning of the surface from the particle functional groups) and better contact between the polymer and filler particles [22, 23].

CMs with a hybrid filler demonstrate decreasing of δ from 1.07 to 0.82 nm (from 1.32 to 1.05 nm) for w  = 10 × 10 nm ² (w  = 40 × 40 nm ² ).

As we can see from Fig. 7 and Table 3, the polymer layer thickness δ for CMs with a hybrid filler is the smallest regardless of the magnitude of the tunneling cross section, despite higher amount of a conductive chains in CNT-based CMs.

Conclusions

It has been found that two percolation thresholds are formed in polymer solution with nanocarbon with low viscosity. The first is a quasi-dynamic percolation transition which nature is associated with the movement of light separate nanocarbon particles until the mixture is cured. The second percolation transition is static, described by the classical theory of percolation and allowed us to calculate the number of conductive chains and the contact resistance between the filler particles in terms of the model of effective electrical resistivity. It has been found that there is a synergistic effect above the percolation threshold for CMs with a hybrid filler (namely, with the carbon nanotubes and graphite nanoplatelets). It has been shown that a synergistic effect for the CMs with a hybrid filler is possible due to reducing contact resistance between the particles of both fillers, which may be associated with a decrease of the polymer layer thickness between the particles and appearance of moderate amount of the conductive chains with increase of the number of particles involved in a single chain.

Modelo de retención de TaO / HfO x y TaO / AlO x RRAM con características de interruptor autorrectificante Promoción de la detección de acetona de un nanobelt de SnO2 individual por parte de Eu Doping