Convertidor de polarización con birrefringencia controlable basado en metauperficie híbrida de grafeno totalmente dieléctrico

Antecedentes

La investigación en nanofotónica se está desplazando hacia elementos totalmente dieléctricos, particularmente en el diseño de metasuperficies de manipulación de luz sintonizables y experimentalmente factibles [1, 2]. El objetivo principal es integrar tales metasuperficies en dispositivos de detección nanofotónicos. El cambio de enfoque hacia las metasuperficies dieléctricas se debe a las bajas pérdidas radiativas y óhmicas exhibidas en el silicio y otros materiales dieléctricos en comparación con las metasuperficies plasmónicas. En consecuencia, se han propuesto previamente estructuras plasmónicas especiales que utilizan resonancias en modo atrapado de alta Q para mejorar la eficiencia de transmisión [2-5]. La reducción de la pérdida se logra mediante la interferencia entre los modos eléctricos y magnéticos discretos o mediante la ruptura de la simetría en los elementos metálicos. Se desarrolla un acoplamiento débil en el espacio libre que mejora la reducción de pérdidas [1, 6]. Materiales que muestran resonancia magnética como titania (TiO ₂ ), el nitruro de silicio y el germanio muestran buenas propiedades ópticas en varias regiones del espectro electromagnético debido a las bajas pérdidas [7-9]. En particular, tienen baja dispersión visible y fuertes propiedades electroópticas que les permiten ser utilizados en el diseño de elementos ópticos de metasuperficie de bajo contraste.

Recientemente, se han propuesto con éxito metasuperficies de resonancia Fano basadas en grafeno para dispositivos de manipulación de luz como moduladores [10-13], absorbentes [14, 15], dispositivos de luz lenta [16, 17] y capas [16, 18], así como otros. En estos dispositivos, las pérdidas radiativas se mitigaron como resultado de una fuerte interacción entre la monocapa de grafeno y el campo eléctrico confinado en los espacios resonantes. El grafeno ofrece propiedades notables que incluyen conductividad óptica sintonizable y alta movilidad del portador. Esto le permite soportar estructuras resonantes de alta Q con pérdidas radiativas suprimidas [19, 20]. Por otro lado, las metasuperficies metálicas utilizan elementos de sublongitud de onda para mejorar el confinamiento del campo eléctrico y crear cambios abruptos en la fase, amplitud y polarización de la luz que incide.

El resonador de anillo dividido (SRR) es un elemento de metasuperficie plasmónica común debido a su naturaleza de resonancia de inductancia-capacitancia que permite su flexibilidad para ajustar las propiedades ópticas. De manera similar, otras metasuperficies dieléctricas también emplean el SRR como la unidad de metasuperficie básica debido a su capacidad de sintonización y fabricación [21, 22]. Otras formas de elementos, como las “ranuras en Z” en las películas de silicio, también se han diseñado como divisores de polarización [23]. Sin embargo, las metasuperficies metálicas tienen altas pérdidas óhmicas y baja transmitancia que reducen su eficiencia de manipulación de la luz [24, 25].

Metadispositivos totalmente dieléctricos y convertidores de polarización de rejilla de gradiente, propuestos por Chen et al. y Kruk et al., han mostrado eficiencias notables ∼ 99 % [26, 27]. Las estructuras exhiben altas relaciones de birrefringencia, 0.35 y 0.9, en las regiones de terahercios e infrarrojo cercano, respectivamente. Sin embargo, no se propusieron mecanismos de ajuste de birrefringencia. En este trabajo, la sintonización y la conmutación de la birrefringencia se demuestran a través de la polarización del voltaje de la puerta, mientras que la flexibilidad de la estructura se muestra a través de la variación de dimensión. Normalmente, las metasuperficies construidas a partir de antenas de alto índice de refracción están limitadas por la presencia de reflejos posteriores parciales debido al desajuste de impedancia. Un método para superar este desafío es diseñar metasuperficies de silicio con fuertes resonancias de tipo Mie eléctricas y magnéticas localizadas de modo que se puedan realizar transmisiones cercanas a la unidad [28-30]. Las metasuperficies de alto contraste, por otro lado, tienen mayores eficiencias pero menor resolución espacial para realizar perfiles precisos de fase o polarización a lo largo de las líneas de rejilla [31, 32].

En este trabajo, se muestra una metasuperficie totalmente dieléctrica con un factor Q alto basado en el modo magnético atrapado. La celda unitaria propuesta está compuesta de dipolos rectangulares asimétricos en forma de cruz hechos de silicio, grafeno y sustrato de sílice. La capa de grafeno está intercalada entre el silicio y la sílice. El control de la polarización de la luz se logra a través de las propiedades intrínsecas del grafeno y las dimensiones del silicio, mientras exhibe características de placa de cuarto de onda. Por lo tanto, una luz incidente con polarización lineal se convierte en una luz con polarización circular con una alta tasa de conversión de polarización (PCR) en el infrarrojo cercano (> 95 % ). Además, el estado de polarización circular de la luz dispersa se puede conmutar entre un estado de polarización circular a la derecha (RCP) y un estado de polarización circular a la izquierda (LCP), a través de una polarización de voltaje de puerta externa. Este control dinámico de polarización aumenta los grados de libertad de la estructura y puede tener un gran impacto en los dispositivos fotónicos CMOS. Se ha utilizado el método de elementos finitos, utilizando COMSOL Multiphysics, para modelar la celda unitaria y analizar el rendimiento de la metasuperficie.

Métodos

La presentación esquemática de la celda unitaria de la estructura se muestra en la Fig. 1a. Consiste en una antena de silicio en forma de cruz sobre una capa de grafeno y un sustrato de sílice. La permitividad relativa del silicio y la sílice son 12,25 y 2,25, respectivamente [33]. Todas las dimensiones se muestran en el título de la Fig. 1a. Primero, para obtener una resonancia aceptable, la periodicidad P _x =600 nm fue fijo y P _y barrido a través de varios valores. Las dimensiones internas L ₁ =440 nm y L ₂ =370 nm también se mantuvieron fijos, pero luego se optimizaron para el ajuste de fase. La altura h =110 nm y ancho W =60 nm se mantuvieron fijos a lo largo de las simulaciones. Se utilizó una luz que normalmente incide desde las fuentes del puerto, límites periódicos y una capa perfectamente combinada en el extremo de salida.

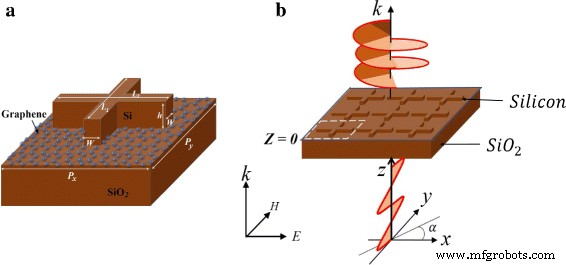
Ilustraciones esquemáticas. a. Dimensiones de la celda unitaria: L ₁ =450 nm, L ₂ =370 nm, h =110 millas náuticas, ancho =60 nm, P _x =600 nm y P _y =560 nm. b. Incidente de luz polarizada linealmente en un ángulo de polarización, α , convertida en luz polarizada circularmente a través de la estructura

Las propiedades de transmisión de la luz se definieron en función de los campos eléctricos dispersos E _i ( yo = x , años ), es decir, \ (T_ {xx} =\ left | \ frac {E_ {x}} {E_ {0}} \ right | \), \ (T_ {yy} =\ left | \ frac {E_ {y }} {E_ {0}} \ right | \), Φ _xx =arg ( E _x ) y Φ _yy =arg ( E _y ), donde T _ii ( yo = x , años ) son coeficientes de transmisión y Φ _ii ( yo = x , años ) son componentes de fase. Luego definimos el retardo de fase como \ (\ Delta \ Phi =\ text {arg} \ left (\ frac {E_ {x}} {E_ {y}} \ right) =\ Phi _ {xx} - \ Phi _ {yy} \) y lo calculé a una distancia z =1,2 μ m de la superficie. Una metasuperficie birrefringente manipula el estado de polarización de la luz incidente introduciendo un retardo de fase en uno de los componentes del campo de transmisión. Según el principio de Huygens, la estructura crea una discontinuidad de fase y un retraso de fase entre Φ _xx y Φ _yy de la luz transmitida \ (E =E_ {x} e ^ {i \ Phi _ {xx}} \ hat {x} + E_ {y} e ^ {i \ Phi _ {yy}} \ hat {y} \ ). Si el retardo de fase introducido es de 90 ° o - 90 °, se producen luces LCP o RCP, respectivamente, confirmando el funcionamiento del QWP como se ilustra en la Fig. 1b. En general, la onda transmitida a través de la metasuperficie está polarizada elípticamente:

$$ \ frac {x ^ {2}} {E_ {x} ^ {2}} + \ frac {y ^ {2}} {E_ {y} ^ {2}} - 2 \ frac {xy} {E_ {x} E_ {y}} \ cos \ Delta \ Phi =\ sin ^ {2} \ Delta \ Phi. $$ (1)

Normalmente, las propiedades ópticas del grafeno se presentan a través de su conductividad, σ , caracterizado por las transiciones entre bandas e intrabandas: σ = σ _yo + σ _D , donde σ _yo y σ _D son las conductividades interbanda e intrabanda, respectivamente. Un cambio de densidad de carga superficial, n _s , en el grafeno varía la población de electrones en el grafeno y la energía de Fermi, es decir, \ (E_ {F} =\ hbar \ nu _ {F} (\ pi n_ {s}) ^ {1/2} \), donde ν _F =10 ⁶ m / s es la velocidad de Fermi de los electrones. Modelamos el grafeno como una monocapa a granel de celdas de malla de espesor, δ =1 nm, y dimensiones en el plano, 1 nm × 1 nm. La permitividad en el plano se calculó dentro de las aproximaciones de fase aleatorias a temperatura ambiente:\ (\ epsilon _ {g} (\ omega) =1+ \ frac {i \ sigma} {\ omega \ epsilon _ {0} \ delta} =\ epsilon '+ i \ epsilon' '\), donde ε ^′ y ε ^″ son las partes real e imaginaria de la permitividad, respectivamente, definidas como funciones de la energía del fotón incidente \ (E =\ hbar \ omega \) y E _F :

$$ {} \ begin {align} {\ epsilon} ^ {\ prime} _ {\ mathrm {g}} &=1+ \ frac {e ^ {2}} {8 \ pi E {\ epsilon} _ { 0} \ delta} \ ln \ frac {(E + 2 | {E} _ {F} |) ^ {2} + {\ Gamma} ^ {2}} {(E-2 | {E} _ {F } |) ^ {2} + {\ Gamma} ^ {2}} - \ frac {e ^ {2}} {\ pi {\ epsilon} _ {0} \ delta} \ frac {| {E} _ { F} |} {{E} ^ {2} + \ left (\ frac {1} {\ tau} \ right) {~} ^ {2}}, \ \ \ text {y} \ end {alineado} $ $ (2) $$ {} \ begin {alineado} {\ epsilon} ^ {\ prime \ prime} _ {\ mathrm {g}} ~ =&~ \ frac {{e} ^ {2}} {4 E {\ epsilon} _ {0} \ delta} \ left [1+ \ frac {1} {\ pi} \ left \ {{\ tan} ^ {- 1} \ frac {E-2 | {E} _ { F} |} {\ Gamma} - {\ tan} ^ {- 1} \ frac {E + 2 | {E} _ {F} |} {\ Gamma} \ right \} \ right] \\ &+ \ frac {{e} ^ {2}} {\ pi E {\ epsilon} _ {0} \ delta \ tau} \ frac {| {E} _ {F} |} {{E} ^ {2} + \ izquierda (\ frac {1} {\ tau} \ derecha) {~} ^ {2}}, \ end {alineado} $$ (3)

donde Γ =110 meV es energía que conduce a la ampliación de la transición entre bandas en el infrarrojo cercano y τ es la tasa de dispersión de portadores libres. Se supone que el parámetro \ (\ frac {1} {\ tau} \) es cero debido al predominio de las transiciones entre bandas sobre las transiciones dentro de la banda en el infrarrojo cercano [1].

Resultados y discusión

Control de birrefringencia a través de la energía de Fermi y las dimensiones de la estructura

Primero, se simuló la metasuperficie totalmente dieléctrica sin capa de grafeno y se obtuvieron los espectros de transmisión que se muestran en la Fig. 2a. La estructura fue iluminada por una luz incidente linealmente polarizada (LP), en un ángulo de polarización, α , como se ilustra en la Fig. 1b. Los resultados de transmitancia de la Fig. 2a muestran una resonancia estrecha con un factor Q elevado. Esto se atribuye a la excitación de modos magnéticos atrapados. Hay un fuerte campo eléctrico en el plano en la longitud de onda de resonancia λ =1,49 μ m a lo largo de los bordes de la antena (Fig. 2b). Los campos eléctricos en el plano son antiparalelos y causan un efecto de interferencia destructivo entre las respuestas del dipolo eléctrico y magnético. Los componentes de la luz LP incidente en un ángulo de polarización, α =48 °, provocan un acoplamiento débil entre los modos electromagnéticos atrapados y la luz del espacio libre. Además, la fuerte penetración del campo en el dipolo de silicio da como resultado un cambio de fase brusco y un acoplamiento mejorado entre la onda plana incidente y la corriente de desplazamiento circulante. Se produce una fuerte resonancia magnética y un cambio de fase abrupto en la longitud de onda de resonancia como se muestra en la Fig. 3a, b. El modo de dipolo magnético está influenciado por la corriente de desplazamiento circular más que el modo eléctrico, que se debe principalmente al acoplamiento entre los dipolos de antena vecinos. Además, Kirshav et al. demostraron que la resonancia magnética está influenciada por la dimensión y la forma de la estructura [34]. Por ejemplo, en nuestra estructura, las dimensiones laterales y la longitud de onda de la luz incidente se pueden relacionar a través de \ (L_ {i} (i ~ =~ 1,2) \ approx \ frac {\ lambda} {n _ {\ text { si}}} \), donde L _i ≈440 nm y n _si =3.5.

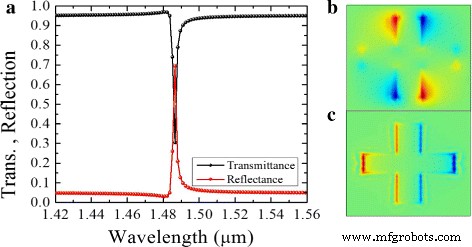
un Transmisión y reflexión para la estructura dieléctrica sin grafeno. b , c . Campos eléctricos en el plano E _x (b) y E _v (c), calculado a la longitud de onda de resonancia λ =1,49 μ m

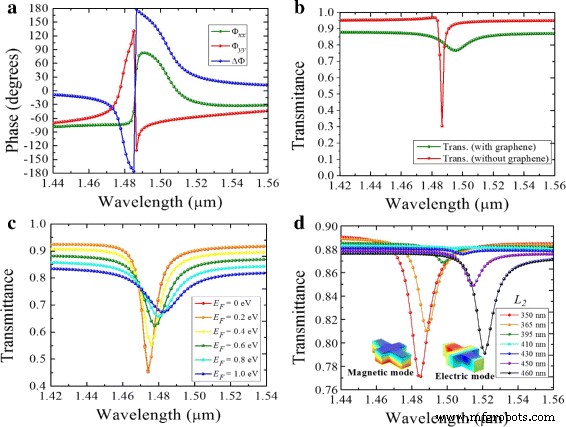
un Componentes de fase y retardo de una metasuperficie totalmente dieléctrica sin grafeno. Transmitancia representada en función de la longitud de onda para L ₁ =440 nm, L ₂ =370 nm y W =60 nm, para b estructura sin grafeno y con grafeno ( E _F =0,8 eV), c variando la energía de Fermi, y d variando L ₂ de 350 a 450 nm. Ruptura de simetría en L ₂ =410 nm divide dos modos dominantes:magnético y eléctrico

Cuando se inserta la capa de grafeno entre el sustrato y la nanoantena, se reduce la corriente de desplazamiento circulante dentro de la antena de silicio y se mejora el campo eléctrico de la superficie. Esto corresponde a la condición donde la polarización del campo eléctrico incidente es antiparalela en los límites opuestos de la nanoantena que da lugar a un acoplamiento débil con las corrientes de desplazamiento circulantes dentro del elemento. El grafeno introduce una conducción mejorada en la superficie entre el silicio y el sustrato de sílice. Se produce un acoplamiento más fuerte con el campo eléctrico en el plano en comparación con el acoplamiento con la corriente de desplazamiento dentro del elemento. Debido a este efecto, los campos eléctricos antiparalelos, que de otro modo causarían interferencia destructiva en la superficie, se reducen y el factor Q cae significativamente, como se muestra en la Fig. 3b. La longitud de onda de resonancia también cambia ligeramente de λ =1,49 μ ma λ =1,5 μ m debido a la reducida penetración en el silicio. En la Fig. 3c, se muestra el efecto de variar la energía Fermi del grafeno. Para un grafeno sin dopar ( E _F =0 eV), hay una fuerte resonancia en λ =1,5 μ m que disminuye a medida que aumenta el nivel de dopaje. La transición entre bandas domina cuando el nivel de Fermi es bajo y el grafeno exhibe características dieléctricas con un ε más grande. ^′ . Sin embargo, cuando E _F aumenta, se bloquean varios canales de transición entre bandas; las transiciones intrabanda causan la respuesta inductiva del grafeno y disminuyen su absorción [1, 20]. Vale la pena señalar que con la capa inferior de grafeno y las dimensiones adecuadas de la estructura de silicio, los modos dipolo magnético y eléctrico se pueden mejorar en fuerza, lo que lleva a una alta eficiencia de dispersión [34]. Las antenas de silicio exhiben resonancias acopladas de dos longitudes de onda cercanas alrededor de la resonancia, como se muestra en la Fig. 3d. En λ =1,48 μ m, la antena muestra el acoplamiento de dipolos magnéticos inducidos, mientras que en λ =1,52 μ m, el acoplamiento es entre los modos eléctricos. Los dos modos ocurren cuando la simetría de la antena cambia de x a y orientaciones en L ₂ ≈410 nm. La dimensión L ₂ se barrió a través de un rango de valores entre 350 y 480 nm manteniendo L ₁ fijado a 440 nm.

El efecto del grafeno es beneficioso para sintonizar los componentes de fase y el retardo de fase de los campos eléctricos transmitidos. En primer lugar, los componentes de la luz LP incidente se descomponen en los brazos ortogonales de la antena de silicio. Cada resonancia de dipolo imprime un patrón de fase diferente en la luz dispersa. Específicamente, cerca de la resonancia, cada resonancia dipolo cambia la fase del campo eléctrico incidente en el rango [- π , π ]. Con las dimensiones adecuadas de la antena, se obtiene una diferencia de fase de 90 ° como se muestra en la Fig. 4a. El coeficiente de transmisión correspondiente se muestra en la Fig. 4b. Se nota que el punto de intersección T _xx = T _yy ocurre cerca de la resonancia, definiendo una condición ideal de QWP. Además, barriendo diferentes valores de la longitud L ₂ manteniendo L ₁ fijo ( L ₁ =440 nm), se pueden variar las amplitudes de resonancia asociadas con diferentes modos eléctricos y magnéticos. Se obtuvo un rango de ancho de banda de fase aceptable dentro de ± 10 ° cuando L ₂ =365 nm para RCP y L ₂ =450 nm para LCP, como se muestra en la Fig. 4c. En segundo lugar, en la Fig. 4d, al variar la energía de Fermi del grafeno, el ancho de banda de fase cambia en consecuencia. En λ =1,48 μ m, el grafeno sin dopar ( E _F =0 e V ) provoca una alta penetración de campos eléctricos en los dipolos de silicio y una gran diferencia de fase entre las x y y se producen componentes de la luz dispersa (≈150 °). Sin embargo, como E _F se aproxima a 0,8 e V , las propiedades en el plano ( ε _x = ε _y ) aumentan la conductividad superficial del grafeno, lo que resulta en una menor penetración en el silicio y una Δ Φ ≈90 ° en λ =1,49 μ m.

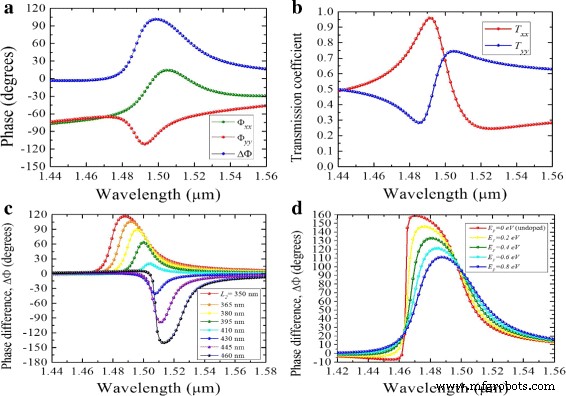
un Componentes de fase y retardo de una metasuperficie totalmente dieléctrica / grafeno y b los coeficientes de transmisión correspondientes T _xx y T _yy . Retardo de fase representado en función de la longitud de onda para L ₁ =440 nm, L ₂ =370 nm y W =60 nm, para c variando la energía Fermi y d variando L ₂ de 350 a 450 nm

Los parámetros de Stokes calculados y las dimensiones de la elipse de polarización para la estructura híbrida con L ₁ =450 nm, L ₂ =370 nm y W =60 nm se muestran en la Fig. 5a, b. Se observa que, lejos de la longitud de onda de resonancia, la polarización de la luz transmitida permanece sin cambios con respecto a la de la luz incidente. Sin embargo, cerca de la resonancia, el estado de polarización cambia a circular para una luz LP incidente. En λ =1,5 μ m, la relación del parámetro de Stokes | S ₃ / S ₀ | ≈ ± 1, donde un valor + 1 indica un RCP perfecto y un - 1 indica una salida de LCP perfecta. Aquí, S ₀ =| E _x | ² + | E _y | ² y S ₃ =2 E _x E _y sin Δ Φ son los parámetros de Stokes. El grado de intensidad de transmisión está determinado por S ₀ , es decir, un valor> 50 % es aceptable. La Figura 5c muestra la eficiencia de la PCR calculada a partir de los coeficientes de transmisión:

$$ \ text {PCR} ~ =~ \ frac {T_ {yx} ^ {2}} {T_ {yx} ^ {2} + T_ {xx} ^ {2}}, $$ (4)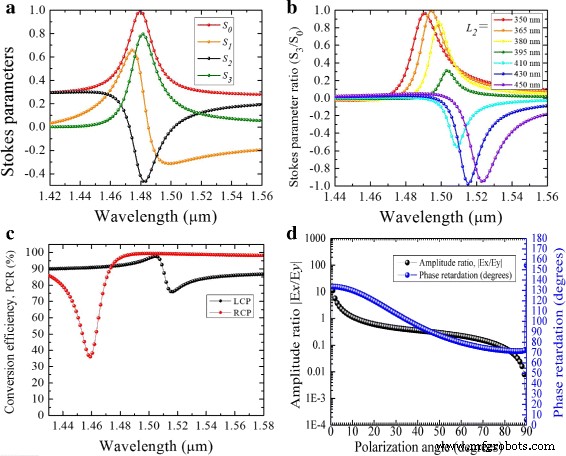

un Variación de los parámetros de Stokes contra la longitud de onda para un ángulo de polarización incidente α =48 °. b . Relación del parámetro de Stokes ( S ₃ / S ₀ ) variación en función de L ₂ en α indicado en a , c Relación de conversión de polarización calculada para una luz incidente con polarización lineal. d . Relación de amplitudes y diferencia de fase en la longitud de onda λ =1,5 μ m en función del ángulo de polarización

donde T _yx y T _xx son términos cruzados y de copolarización, respectivamente. Dentro del rango de longitud de onda λ =1,48 μ my λ =1,51 μ m, la eficiencia es ≈96 % para RCP y ≈90 % para salidas LCP. Sin embargo, en λ =1,52 μ m, la eficiencia cae ligeramente a ≈80 % para LCP. Como se muestra en la Fig. 5d, la estructura es insensible al ángulo de polarización de la luz LP incidente. Relación de amplitud aceptable E _x / E _y ≈1 y cambio de fase Δ Φ ≈90 ° se obtienen en una amplia gama. Cuando α =48 °, se obtiene una condición QWP precisa

Además, el perfil de la fase de transmisión que define la forma de birrefringencia se calculó en función de las periodicidades P _i ( yo = x , años ) en la longitud de onda λ =1,49 μ metro. En la Fig. 6a, el retardo de fase sintonizable de la estructura se puede obtener a lo largo de la diagonal donde las dos periodicidades muestran una relación inversa. También vale la pena señalar que el retardo de fase ( Δ Φ ≈90 °) ocurre en la región donde la transmitancia es superior al 80%, como se muestra en la Fig. 6b. El silicio y la sílice tienen baja dispersión e índices de refracción relativamente altos, por lo que soportan una baja absorción en las longitudes de onda más cortas [8]. De manera similar, la salida de fase se puede controlar a través de un voltaje de puerta externo.

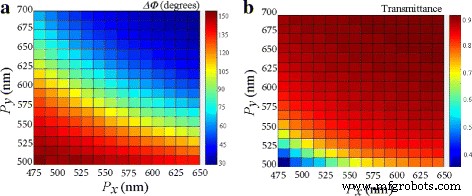
un - b Variación de periodicidades P _x y P _y en λ =1,5 μ metro. un Fase de transmisión y b transmitancia

Conmutación de birrefringencia a través de polarización de voltaje de puerta

Aplicación de la polarización del voltaje de la puerta en y -Los planos de la estructura de silicio / grafeno se diseñaron como se muestra en la Fig. 7a. Al cambiar el voltaje de la puerta entre un valor de polarización directa y un valor de polarización inversa, la luz LP incidente se convierte dinámicamente en estados RCP y LCP de las luces dispersas, respectivamente. El voltaje de polarización controla la velocidad de Fermi de los electrones, ν _F y cambia la dirección del flujo de electrones. Además, el voltaje de polarización cambia la densidad del portador del grafeno, lo que a su vez conduce a un cambio en su conductividad eléctrica y permitividad. En esta configuración, la estructura forma un modelo de condensador de placa cuasi-paralelo con una capacitancia electrostática por unidad de área, C , definido como C = ε _si ε ₀ / P _x , donde ε _si es la permitividad dieléctrica del silicio. La energía de Fermi, \ (E_ {F} ~ =~ \ hbar \ nu _ {F} \ sqrt {\ pi n_ {s}} \), también se modula. La densidad de carga ( n _s ) y la capacitancia electrostática por unidad de área ( C ) escalar la energía de Fermi a través del voltaje de la puerta, es decir, n _s = C V _G / e . En consecuencia, un incremento en P _x Disminuye tanto la concentración de portadores en el grafeno como la capacitancia por unidad de área. Como resultado, como se muestra en la Fig. 7b, la posición del retardo de fase se desplaza hacia el rojo, de acuerdo con la teoría de la perturbación en el infrarrojo medio [35].

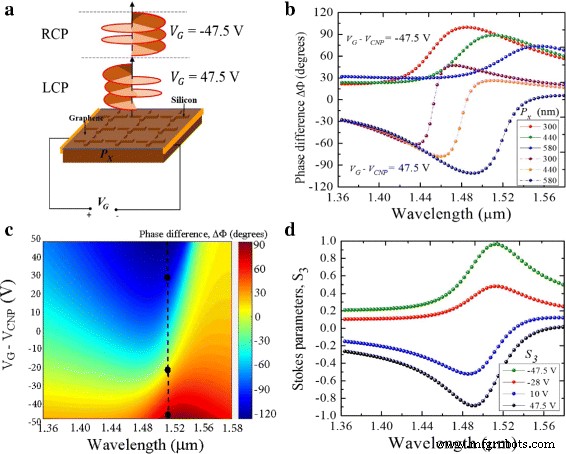
un Ilustración esquemática de la conmutación silicio / grafeno del estado de polarización a través de la polarización del voltaje de la puerta. b. Diferencia de fase simulada en función de la polarización del voltaje de la puerta. c. Diferencia de fase mostrada como función de periodicidad P _x y voltaje de la puerta. d. Parámetro de Stokes S ₃ espectros que muestran los dos estados de polarización circular definidos por los diferentes voltajes de puerta

En λ =1,5 μ m, los dos estados de polarización circular se pueden codificar como dos estados binarios, 0 y 1. El estado lógico 0 corresponde a la tensión inversa - 47,5 V mientras que el estado lógico 1 corresponde a la tensión directa 47,5 V , como se muestra en la Fig. 7c. Un pequeño cambio en el retardo de fase, Δ Φ ≈0 °, se puede observar cuando el voltaje de la puerta está en - 25 V (a lo largo de la línea punteada negra de la figura). Esta observación muestra una respuesta no lineal en el cambio de fase a - 47,5, - 25 y 47,5 V , atribuido a una variación en el acoplamiento capacitivo a medida que el grafeno se vuelve más conductor debido a un cambio en la densidad de la portadora y el voltaje de la puerta. En comparación con otras longitudes de onda en el infrarrojo cercano, 1,5 μ m muestra el punto óptimo para cambiar los estados de polarización circular de la luz dispersa.

En la Fig. 7d, los parámetros de Stokes S ₃ ilustra el grado de polarización circular como resultado de la polarización del voltaje de la puerta. Los límites -1 y 1 denotan las conversiones de polarización ideal de un estado lineal a los estados LCP y RCP, respectivamente. Entre las longitudes de onda λ =1,49 μ my λ =1,52 μ m, el grado de polarización circular se acerca a la unidad (> 90 % ) para ambos estados, confirmando la región de operación más apropiada de la estructura como un QWP.

La Figura 8a, b muestra la distribución de fase de z componente del campo eléctrico, calculado a la longitud de onda de diseño λ =1,5 μ m en z =0. La distribución cambia cuando el voltaje se invierte de 47,5 a - 47,5 V . El cambio en la conductividad eléctrica y la densidad del portador del grafeno da como resultado una rotación del modo magnético atrapado alrededor de la estructura de silicio.

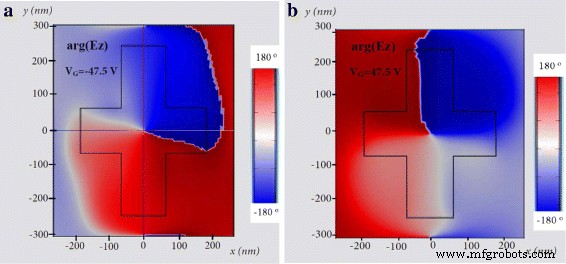
Mapa de fases del componente de campo eléctrico E _z a través de la estructura en forma de cruz de silicio / grafeno en z =0 calculado a la longitud de onda de diseño λ =1,5 μ m, a cuando el voltaje de la puerta es V _G =- 47,5 V y b cuando el voltaje de la puerta es V _G =47,5 V

Conclusiones

En resumen, se ha diseñado numéricamente la capacidad de control de la birrefringencia de un convertidor híbrido de polarización de metasuperficie de silicio / grafeno. Los modos magnéticos atrapados y los factores Q altos se modulan mediante la integración de grafeno y silicio. Se han mostrado dos configuraciones de la estructura híbrida, una con polarización de voltaje de puerta y la otra sin polarización. En la estructura polarizada por voltaje, el rendimiento de birrefringencia se muestra mediante la inversión del voltaje de la puerta. A partir de una luz LP incidente, un voltaje de polarización inversa (- 47,5 V) produce una salida RCP y un voltaje de polarización directa (47,5 V) produce una salida LCP. Por tanto, se consigue un rendimiento de conmutación dinámico. Para la configuración de espacio libre, el rendimiento de QWP se muestra mediante la manipulación de las dimensiones del silicio y el nivel de grafeno de Fermi. En ambos diseños se obtiene un ancho de banda más estable y más amplio que en estructuras sin grafeno. Los diseños muestran mayores grados de conversión de polarización (> 96 % ) en el infrarrojo cercano ( λ =1,45 a 1,54 μ metro). A diferencia de las metasuperficies plasmónicas, estos logros demuestran una alta eficiencia sin pérdidas radiativas y óhmicas. Además, las estructuras son compactas y tienen un grosor ultrafino, apropiado para la compatibilidad e integración con CMOS y dispositivos fotónicos. Mientras tanto, el grafeno es factible y se puede cultivar mediante deposición de vapor químico sobre el sustrato, mientras que la estructura de silicio se puede fabricar utilizando métodos litográficos estándar.

Modulador de electroabsorción de polarización de plasma superficial insensible a la polarización basado en óxido de estaño indio Epsilon-Near-Zero Funcionamiento estable de modo único del láser de cascada cuántica de retroalimentación distribuida mediante recubrimientos de facetas de reflectividad optimizada