Efecto óptico no lineal mejorado en células de cristal líquido híbridas basadas en cristal fotónico

Resumen

La respuesta óptica no lineal de las células de cristal líquido (LC) híbridas fotorrefractivas se ha estudiado mediante una técnica holográfica dinámica en una disposición de mezcla de dos ondas. Las células LC incluyen sustratos de silicio no uniformes que comprenden un cristal fotónico de rango micrométrico. Se coloca una fina capa de LC entre el sustrato de silicio y un sustrato de vidrio plano cubierto por un electrodo transparente (ITO). Se indujo una rejilla de difracción dinámica en el volumen de LC mediante la mezcla de dos ondas de rayos láser con la aplicación simultánea de un campo eléctrico de CC a la celda. Se desarrolló un modelo teórico de autodifracción Raman-Nath. Este modelo permite el cálculo de características ópticas no lineales en muestras delgadas sobre la base de datos experimentales de mezcla de dos ondas y teniendo en cuenta las pérdidas de luz por absorción y / o dispersión. Las células LC híbridas demuestran un fuerte efecto óptico no lineal, prospectivo para muchas aplicaciones en microsistemas electro-ópticos, como SLM, así como en sistemas multicanal.

Antecedentes

Entre las principales ventajas de los sistemas de procesamiento óptico se encuentra su capacidad para utilizar el elevado ancho de banda temporal y espacial de la fotónica. Un componente fundamental en estos sistemas es un dispositivo que modula la luz. Los moduladores de luz espacial (SLM), que imponen información sobre los campos de datos ópticos en los sistemas de procesamiento de información óptica, durante mucho tiempo se han considerado esenciales para la explotación eficiente de la velocidad, el procesamiento en paralelo y las capacidades de interconexión inherentes a la óptica. Estos dispositivos generalmente modifican la fase, polarización, amplitud y / o intensidad de una distribución espacial de la luz en función de la información de impulsión eléctrica o la intensidad de otra distribución de la luz [1]. Las ventajas de los materiales electroópticos de cristal líquido para SLM incluyen su alta birrefringencia y operación de bajo voltaje. La colocación de cristales líquidos sobre circuitos integrados de silicio se propuso a principios de la década de 1980 para producir pantallas portátiles [2]. Debido a la fabricación más amplia de circuitos integrados de silicio, que pueden contener fotodetectores, amplificadores y elementos de memoria, el SLM de cristal líquido electroóptico sobre silicio (LCoS) se convirtió en una herramienta estándar en la mayoría de los laboratorios ópticos. El siguiente paso muy deseado sugiere el manejo de información totalmente óptica, que podría lograrse mediante la modificación controlada por luz de las propiedades ópticas del medio. Muchos de los SLM direccionados ópticamente adoptaron la estructura sándwich básica con el fotoconductor transfiriendo un voltaje de polarización aplicado al sándwich a un material modulador, por ejemplo, cristales líquidos en la válvula de luz de cristal líquido (LCLV) [3].

Casi todos los efectos ópticos no lineales existentes se han observado en las composiciones de LC dopadas con colorante, en las que las moléculas de colorante absorbente desencadenan la reorientación del director de LC [4]. Alternativamente, la acción de la luz sobre las moléculas fotosensibles afecta el parámetro de orden de LC que, a su vez, resulta en cambios sustanciales y rápidos de los índices de refracción locales de LC [5]. El año pasado, los populares centros fotosensibles se convirtieron en nanopartículas incrustadas en el volumen de LC [6]. Los sistemas LC que no absorben también han atraído mucho interés como las válvulas de luz LC fotorrefractivas de nemática pura. El principal mecanismo óptico no lineal en LC es la reorientación colectiva de moléculas en una gran parte de LC bajo excitación láser que a menudo aparece con el campo eléctrico aplicado. En el presente trabajo utilizamos LC nemática pura. El mecanismo óptico no lineal en células como las de LC sugiere un efecto fotorrefractivo inducido por la superficie, que cambia la orientación de las moléculas de LC en la masa iniciada desde la superficie. Este efecto se investigó en células LC que contienen diferentes materiales de superficie, como capas de polímero fotorrefractivo [7, 8], capas conductoras con impurezas incrustadas [9], placas de metales nobles [10] y cristales fotorrefractivos [11]. Como regla general, la orientación inicial de las moléculas en una superficie fue la plana. Otro tipo de células, que exhiben un efecto fotorrefractivo inducido por la superficie, consisten en sustratos de vidrio simples cubiertos con electrodos ITO y llenos de un LC nemático puro, pero la característica principal estudiada es la orientación homeotrópica de las moléculas [12, 13]. Tal efecto se estudia en el presente trabajo. Sin embargo, utilizamos células híbridas en las que uno de los sustratos es un cristal fotónico hecho de silicio. La mejora de las propiedades físicas de los materiales depositados en superficies nano o microestructuradas, incluidas las propiedades ópticas, eléctricas y otras, se convierte en una de las direcciones prioritarias de la nanociencia fundamental. En nuestra investigación, investigamos la posibilidad de fortalecer el efecto óptico no lineal en una celda LC debido a la influencia de una superficie microestructurada de un sustrato, que forma la celda.

Para investigar las propiedades ópticas no lineales en células LC híbridas que contienen una superficie reflectante, aplicamos la técnica holográfica dinámica basada en la mezcla de dos ondas de rayos láser en la geometría de reflexión [14]. Se sabe que la holografía dinámica se basa en tres efectos principales, que actúan simultáneamente:(1) creación de un patrón de interferencia periódica dentro de un medio no lineal con la ayuda de dos o más rayos láser coherentes; (2) modulación del índice de refracción bajo la acción de este patrón de interferencia; en nuestro caso, significa inducir una rejilla dinámica de fase dentro de un medio no lineal; (3) autodifracción de los rayos de grabación en la rejilla dinámica. Hasta ahora, la mezcla de ondas se conoce como una técnica eficaz para muchas aplicaciones en óptica no lineal (ver, por ejemplo, [15]). Baste mencionar multiplexación espacial y conmutación de rayos láser, control totalmente óptico de los parámetros de los rayos, memoria óptica dinámica, lógica, etc. En el presente trabajo demostramos que este método también se puede aplicar como una técnica experimental simple para determinar las características ópticas no lineales de películas delgadas. Hemos desarrollado un enfoque matemático para calcular el coeficiente de refracción no lineal en un medio similar a Kerr, a partir del cual se puede determinar la susceptibilidad óptica no lineal. El modelo matemático cubre la autodifracción de ondas en el régimen Raman-Nath, es decir, para la condición de una rejilla delgada. Este enfoque generalmente se satisface para la mayoría de las muestras delgadas que normalmente tienen un espesor de hasta decenas de micrómetros. Dichos medios incluyen también células LC. Tenga en cuenta que un método alternativo para determinar la susceptibilidad óptica no lineal de materiales transparentes es la técnica de escaneo z [16]. Pero mostramos que el método de mezcla de dos ondas es bastante simple para la realización experimental y es muy adecuado para la investigación de los medios dinámicos, incluido el que funciona solo en la geometría de reflexión.

Métodos

Materiales y muestras

La estructura de las células LC híbridas se muestra en la Fig. 1. La celda híbrida tiene un tipo de tipo sándwich, está formada por sustratos de vidrio y silicio y llena con LC nemática; sus bordes están pegados. El espesor de la capa de LC nemática es de 20 μm. El sustrato de vidrio plano se cubre con un electrodo ITO. El segundo sustrato se corta de una oblea de silicio dopado con fósforo, sus dimensiones son 17 × 17 mm ² . Su resistividad es de 4.5 Ω⋅cm, su espesor es de 380 μm y su orientación es de 〈100〉. El sustrato de silicio contiene dos áreas, a saber, una superficie con una parte microestructurada periódica, que en realidad es un cristal fotónico en el rango de micrómetros, y una parte plana de la superficie.

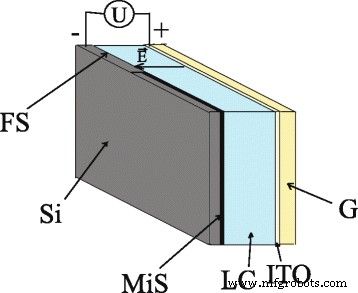
Estructura de una célula LC híbrida:sustrato de silicio ( Si ); superficie de silicio microestructurado ( MiS ); superficie plana de silicona ( FS ); cristales líquidos ( LC ); sustrato de vidrio ( G ); Electrodo ITO ( ITO ); voltaje aplicado ( U ); vector de campo eléctrico (\ (\ overrightarrow {E} \))

Los tres sustratos de Si, usados en nuestra investigación, se muestran en la Fig. 2. Las microestructuras representan picaduras grabadas dispuestas en una matriz cuadrada (los sustratos 1 y 2) o en una matriz triangular (el sustrato 3). Los hoyos son micropirámides cuadradas, que se diferencian por la forma, el tamaño y la disposición. Hay (1) pirámides regulares, (2) pirámides truncadas (pozos) y (3) pirámides ligeramente truncadas. Las micropiramides regulares tienen 2 μm de altura, el mismo lado de la base de 2 μm y una periodicidad de 3 μm. Los pozos tienen parámetros similares, pero están muy compactos. Las pirámides ligeramente truncadas tienen el lado de la base de 1,5 μm y la periodicidad de 3,5 μm. Las microestructuras se formaron en el lado pulido de la oblea de silicio mediante una técnica fotolitográfica estándar seguida de grabado anisotrópico para los sustratos 1 y 3, o por grabado con plasma para el sustrato 2.

Imágenes de superficie de silicio microestructurado realizadas en microscopio óptico. Las micropirámides tienen las siguientes formas:pirámides regulares (1), fosos (2) y pirámides ligeramente truncadas (3)

Se utilizaron dos LC nemáticos:5CB nemático puro (4 × - ( n -pentil) -4-cianobifenilo) y mezcla nemática E7. En todos los casos, la orientación molecular en una capa de cristal líquido es homeotrópica y aparece espontáneamente en las superficies de ITO y silicio con una temperatura de procesamiento que no se mantiene por encima de 50 ° C. Hemos investigado cuatro muestras, que se diferencian por la forma de la microestructura y por el LC utilizado. Las muestras con sustratos de silicio 1 y 2 constan de dos partes:una parte contiene una superficie mal estructurada y la segunda parte es plana. En tales muestras, tenemos la oportunidad de comparar la respuesta no lineal en una celda plana (que contiene una parte plana del sustrato de Si) y en una celda microestructurada (que contiene una parte microestructurada del sustrato de Si).

De esta forma, en nuestros experimentos tenemos las siguientes células híbridas:

1)
M1 abreviado:sustrato de vidrio + sustrato 1 de ITO / 5CB / Si, superficie microestructurada
2)
F1 abreviado:sustrato de vidrio + sustrato ITO / 5CB / Si 1, superficie plana
3)
M2 abreviado:sustrato de vidrio + sustrato ITO / 5CB / Si 2, superficie microestructurada
4)
abreviado F2:sustrato de vidrio + sustrato ITO / 5CB / Si 2, superficie plana
5)
M3 abreviado:sustrato de vidrio + sustrato ITO / 5CB / Si 3, superficie microestructurada
6)
M4 abreviado:sustrato de vidrio + sustrato ITO / E7 / Si 3, superficie microestructurada

Configuración experimental

La Figura 3 muestra el esquema de la configuración experimental, que se basa en el método holográfico dinámico con mezcla de dos ondas. Láser Nd:YAG de semiconductor continuo (duplicación de frecuencia, λ =532 nm, P =52 mW, generación monomodo) es una fuente de luz. Por medio de un divisor de haz BS y un espejo M, la radiación láser se divide en dos haces B ₀ y B ₁ , convergiendo en la celda en un ángulo pequeño θ ≈ 0.01 rad. Las intensidades de entrada I ₀ y yo ₁ se igualan con la ayuda del filtro F1, y en nuestro caso, I ₀ = yo ₁ =3,3 W / cm ² . El diámetro de un punto láser en una celda es de 1 mm.

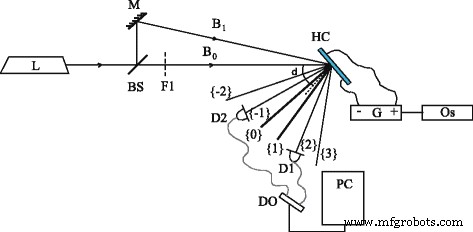
Esquema de configuración experimental:láser ( L ); espejo ( M ); divisor de haz ( BS ); filtro óptico ( F1 ); vigas ( B ₀ ) y ( B ₁ ); fotodiodos ( D1 ) y ( D2 ); célula LC híbrida ( HC ); osciloscopio ( Os ); generador ( G ); oscilógrafo digital ( DO ); computadora ( PC ). Los órdenes de difracción de salida son {0} y {1} los órdenes principales; {−1} y {2} los primeros órdenes de difracción; {−2} y {3} los segundos órdenes de difracción. δ es el ángulo de rotación de la celda

Dos rayos láser B ₀ y B ₁ formar un patrón de interferencia dentro de la muestra. Ambos haces incidentes tienen p lineales polarización. Entonces se crea el patrón de interferencia de modulación de intensidad. La celda LC normal hace que el ángulo δ con la bisectriz de B ₀ y B ₁ . El campo eléctrico de CC se aplica debido a la fuente G con el voltaje U controlado en el rango de 0 a 15 V. El sustrato de vidrio ITO se establece como electrodo positivo. Medimos las intensidades de los primeros órdenes de difracción {-1} y {2} mediante el uso de fotodiodos D1 y D2 mediante un osciloscopio digital DO controlado por computadora. Los ángulos de rotación de la celda se ajustaron para maximizar la señal de difracción y parecían ser δ ≈ 40 - 55 ⁰ para diferentes muestras. Estos resultados coinciden con los experimentos de otros grupos (por ejemplo [9, 12]); la razón de tal efecto está más allá del alcance de nuestro estudio.

Modelo de autodifracción de ondas en aproximación Raman-Nath

La autodifracción de ondas ha sido considerada en varios trabajos [17, 18]. Cuando tiene lugar la autodifracción de dos ondas de entrada en la rejilla delgada de índice de refracción fotoinducida, aparecen muchos órdenes de difracción en la salida. Al medir las intensidades en los primeros órdenes de difracción, se puede calcular la profundidad de modulación de la rejilla ( Δn ). Dado que en el medio similar a Kerr la condición Δn = n ₂ yo ₀ es válido (donde I ₀ es la intensidad del haz de excitación), el coeficiente de refracción no lineal n ₂ es posible calcular.

En esta sección, buscamos la solución para la eficiencia de difracción de los primeros órdenes de difracción en el caso de rejilla de índice de refracción sinusoidal no desplazada. Entonces las intensidades en órdenes simétricos serán iguales. El modelado se parte de la ecuación de onda, en la que tanto el campo eléctrico \ (\ overrightarrow {E} \) como la parte modulada de la permitividad dieléctrica Δε resultante del efecto no lineal similar a Kerr depende de la coordenada z (a lo largo de la propagación de la onda):

$$ {\ nabla} ^ 2 \ overrightarrow {E} \ left (z, t \ right) =\ frac {1} {c ^ 2} \ frac {\ partial ^ 2} {\ partial {t} ^ 2} \ left [{\ varepsilon} _0 + \ varDelta \ varepsilon \ left (z, t \ right) \ right] \ overrightarrow {E} \ left (z, t \ right) $$ (1)

donde c es la velocidad de la luz en el vacío, \ ({\ varepsilon} _0 ={n} _0 ^ 2 \) representa la permitividad dieléctrica de un medio y n ₀ es su índice de refracción. Buscaremos la solución de la ecuación de onda (1) en la suma de todos los órdenes de difracción, que son ondas planas polarizadas en la dirección del eje \ (\ overrightarrow {y} \):

$$ \ overrightarrow {E} =\ frac {1} {2} \ overrightarrow {y} \ left \ {{\ displaystyle \ sum_ {m =- \ infty} ^ {+ \ infty} {\ overrightarrow {A}} _m \ left (z, t \ right) {e} ^ {i \ left [{\ omega} _0 t- \ left ({\ overrightarrow {k}} _ 0- m \ overrightarrow {K} \ right) \ overrightarrow { r} \ derecha]} {e} ^ {- \ frac {1} {2} \ alpha z} + c. c.} \ right \} $$ (2)

donde ω ₀ es la frecuencia de la radiación láser, \ (\ overrightarrow {r} \) es la coordenada y “ c. c . " denota el término conjugado complejo. En nuestra representación, es conveniente expresar el coeficiente de atenuación como α = α _abs + α _sc , que tiene en cuenta las pérdidas de radiación láser tanto por absorción α _abs y dispersando α _s . La Figura 4 muestra el diagrama de vector de onda de la autodifracción en aproximación Raman-Nath. Demuestra que la ola del m -ésimo orden de difracción corresponde a la dirección espacial descrita por el vector de onda \ ({\ overrightarrow {k}} _ m \). Órdenes de difracción m =0 y m =1 pertenecen a dos rayos emocionantes B ₀ y B ₁ . El vector de onda del m -ésimo orden de difracción es \ ({\ overrightarrow {k}} _ m ={\ overrightarrow {k}} _ 0- m \ overrightarrow {K} \), y \ (\ overrightarrow {K} \) es el vector de onda de la rejilla fotoinducida. La modulación de permitividad Δε se define en forma de rejilla:

$$ \ varDelta \ varepsilon \ left (z, t \ right) =\ frac {1} {2} \ left [{\ overrightarrow {\ varepsilon}} _ 1 \ left (z, t \ right) {e} ^ { - i \ overrightarrow {K} \ overrightarrow {r}} + c. c. \ right] $$ (3)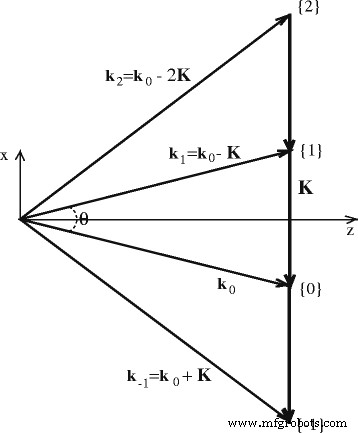

Diagrama de vector de onda de la autodifracción de dos ondas coherentes (descrito por \ ({\ overrightarrow {k}} _ 0 \) y \ ({\ overrightarrow {k}} _ 1 \)) en la aproximación Raman-Nath

Sustituyendo la solución (2) y (3) en la ecuación. (1), se obtiene la relación para una amplitud variable lenta A _m del m -ésimo orden:

$$ \ frac {\ parcial {A} _m} {\ parcial z} + i \ frac {\ izquierda ({k} _0 ^ 2- {k} _m ^ 2 \ derecha)} {2 {k} _ {mz }} {A} _m- \ frac {1} {2} \ alpha \ cdot {A} _m =- i \ frac {k _ {\ upsilon} ^ 2} {4 {k} _ {mz}} \ left [ {\ varepsilon} _1 {A} _ {m + 1} + {\ varepsilon} _1 ^ {*} {A} _ {m-1} \ right] $$ (4)

donde k _υ =2 π / λ es el vector de onda en el vacío, y la marca “∗” denota la conjugación compleja. Dado que en nuestra representación, los principales haces de grabación de las órdenes m =0 y m =1 son idénticos en la entrada, así como en todo el espesor de la muestra, se deduce que ε ₁ es real y no depende de la coordenada z (ver [18]):\ ({\ varepsilon} _1 (t) ={\ varepsilon} _1 ^ {*} (t) \). Para una mayor transformación de la ecuación. (4), introducimos una nueva función \ ({U} _m \ left (z, t \ right) ={A} _m \ left (z, t \ right) \ exp \ left (- \ frac {1} { 2} \ alpha z \ right) \ exp \ left (im \ frac {\ pi} {2} \ right) \), designa T =Exp (- αz ) las pérdidas de intensidad luminosa en el medio, y definen \ ({\ varepsilon} _1 =T {\ tilde {\ varepsilon}} _ 1 \). Introduciendo una nueva variable \ (\ tilde {z} ={k} _ {\ upsilon} / \ left ({n} _0 \ cos \ left (\ theta / 2 \ right) \ right) \ cdot \ left (1 - T \ right) / \ left (2 \ alpha \ right) \), donde θ es el ángulo de convergencia, Eq. (4) puede escribirse como:

$$ 2 \ frac {\ parcial {U} _m} {\ parcial \ tilde {z}} ={\ tilde {\ varepsilon}} _ 1 \ left [- {U} _ {m + 1} + {U} _ {m-1} - i \ frac {2 m \ left (m-1 \ right)} {\ phi} {U} _m \ right] $$ (5)

donde el parámetro ϕ está definido por \ (\ phi =T {\ tilde {\ varepsilon}} _ 1 / \ left (2 {n} _0 ^ 2 {\ sin} ^ 2 \ left (\ theta / 2 \ right) \ right) \) .

En las condiciones de la aproximación Raman-Nath, es posible despreciar el último término de la parte derecha de la ecuación. (5) (Ref. [18]), es decir, 2 m ( m - 1) / ϕ <<1 para cualquier m . Luego, al introducir una nueva variable \ (\ zeta =\ tilde {z} {\ tilde {\ varepsilon}} _ 1 (t) \), obtenemos nuestra ecuación principal en la aproximación Raman-Nath:

$$ 2 \ frac {\ parcial {U} _m \ izquierda (\ zeta, t \ derecha)} {\ parcial \ zeta} + {U} _ {m + 1} \ izquierda (\ zeta, t \ derecha) - {U} _ {m-1} \ left (\ zeta, t \ right) =0 $$ (6)

Esta relación es formalmente una representación bien conocida de la función de Bessel, por lo que su solución puede expresarse mediante funciones de Bessel en la forma:

$$ {U} _m \ left (\ zeta, t \ right) ={\ displaystyle \ sum_ {n =0} ^ {\ infty} {C} _n ^ m (t) {J} _n \ left (\ zeta \ right)} $$ (7)

La Eq. (6) satisface las propiedades de simetría \ ({U} _0 {U} _0 ^ {*} ={U} _1 {U} _1 ^ {*} \) para el par de las vigas principales, así como para todos los pares de los haces difractados (\ ({U} _2 {U} _2 ^ {*} ={U} _ {- 1} {U} _ {- 1} ^ {*} \)). Tenga en cuenta que en z =0, E ₀ (0, t ) = E ₁ (0, t ) ≠ 0, pero E _m (0, t ) =0 para m ≠ 0, 1, y luego intensidades de salida de los primeros órdenes de difracción I _{−1} ( d , t ) y yo _{2} ( d , t ) será igual y estará definido por una fórmula (ver también [18]):

$$ {I} _ {\ left \ {- 1 \ right \}} \ left (d, t \ right) ={I} _ {\ left \ {2 \ right \}} \ left (d, t \ derecha) =T {I} _0 \ izquierda (0, t \ derecha) \ izquierda [{J} _1 ^ 2 \ izquierda (\ zeta \ derecha) + {J} _2 ^ 2 \ izquierda (\ zeta \ derecha) \ derecha] $$ (8)

donde d es el espesor de un medio no lineal; yo ₀ es la intensidad de un rayo láser; J ₁ y J ₂ son las funciones de Bessel del primer tipo de primer y segundo orden, respectivamente. Dado que en nuestro caso, las intensidades I ₀ y yo ₁ son iguales, es decir, 2 I ₀ = yo _láser , en consecuencia, el valor de ζ se puede escribir como:

$$ \ zeta =\ tilde {z} {\ tilde {\ varepsilon}} _ 1 =\ frac {k _ {\ upsilon}} {n_0 \ cdot \ cos \ left (\ theta / 2 \ right)} \ frac {1 - T} {2 \ alpha} {\ tilde {\ varepsilon}} _ 1 \ approx \ frac {k_0} {n_0} \ frac {1- T} {2 \ alpha} 2 {n} _0 \ varDelta n $$ ( 9)

En un medio similar a Kerr Δn = n ₂ yo ₀ , donde n ₂ representa el coeficiente de refracción no lineal, luego el valor final de ζ tiene una forma más simple:

$$ \ zeta =\ frac {2 \ pi} {\ lambda} \ frac {1- T} {\ alpha} {n} _2 {I} _0 $$ (10)

La eficiencia de difracción η del primer orden de difracción se determina como η = yo _{−1} / ( TI ₀ ). Por otro lado, la eficiencia de difracción puede obtenerse experimentalmente midiendo la intensidad I _{−1} y el coeficiente de transmisión de una celda T . La fórmula común (8) es válida para calcular la eficiencia de difracción en un amplio rango. Para eficiencias de difracción más pequeñas, η ≤ 2%, la buena aproximación será solo el primer término polinomial de (8): η ≈ ζ ² / 4. En consecuencia, se puede obtener una relación simple para n ₂ :

$$ {n} _2 =\ frac {\ lambda} {\ pi} \ frac {\ alpha} {1- T} \ frac {\ sqrt {\ eta}} {I_0} $$ (11)

Cabe señalar que la ecuación derivada. (11) tiene la misma forma que la ecuación que se obtiene convencionalmente para el caso de la difracción de un solo haz de sonda de una determinada rejilla de índice de refracción (véase, por ejemplo, la Ref. [19]). Pero para valores grandes de η , que es habitual en las células LC, se deberían utilizar relaciones más precisas (8) y (10) para calcular los valores ζ y n ₂ .

Conociendo el valor n ₂ , se puede definir la susceptibilidad no lineal del medio con la ayuda de la expresión:

$$ {\ chi} ^ {(3)} \ left [\ mathrm {esu} \ right] ={n} _2 \ left [\ frac {\ mathrm {c} {\ mathrm {m}} ^ 2} { W} \ derecha] \ cdot \ frac {9 \ cdot {10} ^ 4} {4 \ pi} c \ cdot {\ varepsilon} _e \ cdot {n} _0 ^ 2 $$ (12)

donde ε _e es la constante eléctrica. En el caso del 5CB nemático, utilizamos el índice de refracción para la orientación homeotrópica de las moléculas n ₀ = n _⊥ =1,51 como el índice de refracción ordinario; de manera similar para la mezcla nemática E7, n ₀ = n _⊥ =1.5268.

El enfoque teórico desarrollado es válido para películas delgadas que poseen una no linealidad óptica similar a Kerr, cuando las pérdidas de luz tanto en la absorción como en la dispersión son grandes. Dado que el método de autodifracción no requiere una fuente de láser adicional como sonda, la mezcla de dos ondas se convierte en un método simple para el diagnóstico de la no linealidad óptica de medios delgados, incluidas las células LC.

Resultados y discusiones

Sugerimos que el mecanismo óptico no lineal en las células híbridas de LC sea un efecto fotorrefractivo inducido por la superficie, que cambia la orientación de las moléculas de LC en la masa iniciada desde la superficie [12, 13]. En los experimentos de mezcla de dos ondas, la muestra se ilumina mediante un patrón de interferencia de luz periódica formado por dos rayos láser coherentes. Este patrón crea una modulación de carga espacial en la interfaz LC-sustrato. La distribución periódica resultante del campo eléctrico en la superficie estimula la modulación de la orientación del director sobre el sustrato. La reorientación de las moléculas comienza en la superficie y se extiende al volumen LC.

El rendimiento experimental típico de mezcla de dos ondas con células LC híbridas se muestra en la Fig. 5. En ausencia de campo eléctrico, observamos una estructura bidimensional regular de los rayos láser principales reflejados desde un sustrato microestructurado de la celda (Fig. 5a ). Después de la aplicación de voltaje de CC, aparecen muchos órdenes de difracción a un lado de cada par de haces principales debido a la excitación de la rejilla de índice de refracción dentro de la celda (Fig. 5b). En el caso de las celdas planas F1 y F2, no existe un patrón de dispersión múltiple, observamos solo una línea central después de aplicar el voltaje. Medimos las intensidades en los primeros órdenes de difracción {-1} y {+2} en la línea central en el estado estacionario para todas las células:células planas y células con superficie microestructurada. Luego calculamos la eficiencia de difracción de acuerdo con η = Ī _{−1} / ( TI ₀ ), donde Ī _{−1} es la intensidad media de dos primeros órdenes de difracción ( Ī _{−1} =( yo _{−1} + yo _{2} ) / 2) y T es el coeficiente de transmisión de la celda.

Patrones típicos de dispersión para dos rayos láser interferentes formados por una celda LC híbrida no lineal con superficie microestructurada. un Patrón de dispersión de una celda híbrida sin campo eléctrico aplicado. b Formación de muchos órdenes de difracción (la autodifracción Raman-Nath) en la aplicación de voltaje eléctrico de CC. La línea central se muestra en ( b ) por una línea de guiones

Tenga en cuenta que el efecto fotorrefractivo inducido por la superficie, explotado en nuestros experimentos, depende en gran medida del ángulo de rotación de la muestra en relación con la bisectriz del ángulo de convergencia entre dos ondas de entrada (ver, por ejemplo, [9, 12, 13]). Así, con la posición normal de la muestra, cuando la placa de la muestra es perpendicular a la bisectriz de las ondas, no se observan órdenes de difracción. Al mismo tiempo, en nuestro caso, cuando la muestra se gira con respecto a esta bisectriz, la rejilla del índice de refracción fotoinducida parece estar desplazada con respecto al patrón de interferencia de luz. Este efecto debería manifestarse en la existencia de transferencia de energía entre órdenes de difracción. En el caso de nuestras células híbridas y dos rayos láser con intensidades de entrada iguales, hemos observado que la diferencia de intensidades en los primeros órdenes de difracción no supera el 10%. Hemos tomado un valor promedio entre estas dos intensidades medidas que se utiliza para cálculos adicionales del coeficiente de refracción no lineal. Este valor pertenece al rango de precisión de nuestras estimaciones de los coeficientes ópticos no lineales. También tenga en cuenta que el modelo matemático desarrollado se reduce a una fórmula resultante bastante simple y no incluye los cambios de fases de onda en un volumen de una capa no lineal. El efecto de la respuesta no local en el medio y la transferencia de energía entre ondas se considerarán cuidadosamente en nuestros próximos trabajos.

En la Tabla 1, recopilamos los parámetros experimentales medidos para las células LC híbridas. El coeficiente de transmisión se define como T = yo ^fuera / Yo ₀ , donde yo ₀ es la intensidad de un solo haz incidente, y I ^fuera es la intensidad del haz de salida. T incluye dos partes: T = R _s T _a , donde R _s tiene en cuenta la pérdida de intensidad por dispersión desde la superficie microestructurada para formar un patrón de luz periódico; y T _a =Exp (- αd _ef ) describe la pérdida de intensidad por absorción durante la propagación de la luz en una gran parte de la celda LC. En la Tabla 1 también presentamos los valores d _ef , que es un espesor efectivo para un haz de propagación en una celda. Tenga en cuenta que en nuestras mediciones descuidamos las pérdidas en la reflexión de la luz desde el límite del vidrio de entrada de una celda.

En la figura 6 se muestran las eficiencias de difracción medidas para todas las celdas en función del voltaje aplicado. Se puede ver que la eficiencia de difracción alcanza su máximo para un cierto voltaje, que difiere en varias celdas; este voltaje es más alto para las células microestructuradas en comparación con las planas (comparar F1 y M1, F2 y M2); así como este voltaje cambia dependiendo de la forma de la microestructura (comparar M1, M2, M3, M4). También enfatizamos que las eficiencias de difracción alcanzan valores bastante grandes en las células LC (hasta un 9% para las células M1 y F1). Usamos valores medidos de η para calcular las características ópticas no lineales de las células LC investigadas, a saber, el coeficiente de refracción no lineal n ₂ y susceptibilidad no lineal efectiva χ ⁽³⁾ , teniendo en cuenta que las células LC poseen una no linealidad óptica similar a Kerr.

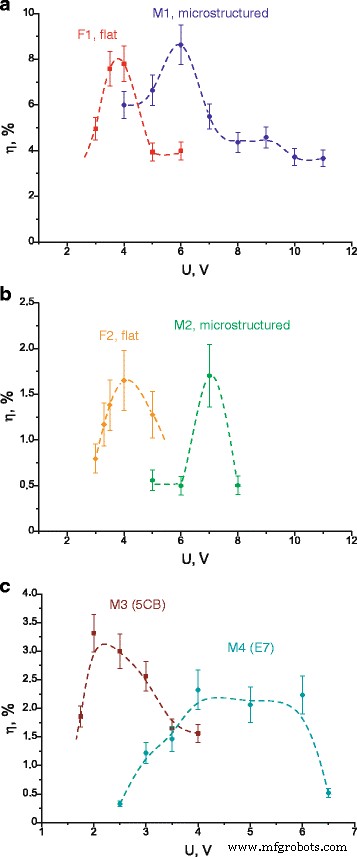
Eficiencia de difracción de primer orden de difracción en función de la tensión aplicada. un Celdas M1 y F1. b Celdas M2 y F2. c Celdas M3 y M4. Líneas discontinuas presentado solo para visualización

Los coeficientes de refracción no lineal calculados a partir de mediciones experimentales de las eficiencias de difracción se muestran en la Fig. 7 para todas las células. En el caso de las celdas M1 y F1, así como M3 y M4, n ₂ se calcula a partir de las fórmulas principales (8) y (10) como las eficiencias de difracción medidas η > 3,5%. Usamos la fórmula aproximada (12) para las celdas M2 y F2, ya que la η obtenida <2%. Obtenemos que el coeficiente máximo de refracción no lineal es mayor en una celda con sustrato microestructurado en comparación con las celdas planas (ver Fig. 7a, b). La Tabla 2 presenta los valores de susceptibilidad no lineal calculados a partir de los valores máximos de n ₂ en la Fig. 7. La susceptibilidad no lineal pareció estar esencialmente mejorada (en un 30-100%) en las células con sustrato microestructurado con respecto a las células hechas de sustratos planos. Las razones que conducen a una mayor profundidad de modulación de la rejilla dinámica en las células que contienen sustratos microestructurados son objeto de investigación adicional. We suppose this effect to be connected with initial reorientation of molecules arising on microstructured surface.

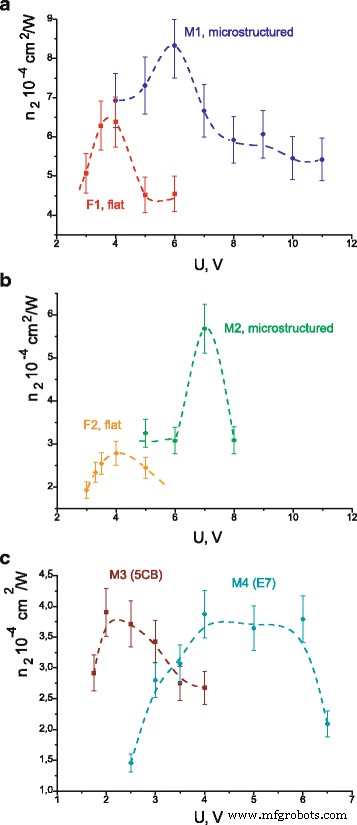
Calculated coefficients of nonlinear refraction in dependence on applied voltage for cells M1 and F1 (a ); M2 and F2 (b ); M3 and M4 (c ). Dashed lines are for the visualisation only

Conclusions

We have investigated the nonlinear optical effect in novel hybrid LC cells based on a silicon photonic crystal. The cell consists of two different materials separated by a thin LC layer with homeotropic orientation of molecules. One material is a glass substrate with ITO electrode. The second one is silicon substrate with periodic microstructured surface. Microstructures in a shape of periodically arranged micro-pyramids are etched on the silicon surface by applying the chemical photolithography method or plasma etching one.

We apply the dynamic holography method with two-wave mixing to define the efficiency of self-diffraction of the dynamic grating induced in LC layer. A theoretical model for the Raman-Nath self-diffraction, offered for calculating the diffraction efficiency in the first diffraction orders, have allowed us to determine the nonlinear refraction coefficient n ₂ , and nonlinear susceptilibity χ ⁽³⁾ of the cells. We have also made a comparative analyses of nonlinear parameters obtained for cells with and without microstructures. Nonlinear susceptibility appeared to be essentially enhanced (by 30 − 100%) in the microstructured cells with respect to the cells made of flat surfaces. The underlying mechanism of the optical nonlinearity is the surface-induced photorefractive effect in the pure nematic LC. The increased modulation depth of the refractive index might be connected with initial reorientation of the molecules arising on the microstructured substrate.

The developed theoretical approach could be valid for determination of nonlinear optical characteristics of thin films possessing Kerr-like optical nonlinearity, in which the losses on the both absorption and scattering are large, as well as in the either transmission or reflection geometries. Photorefractive hybrid LC cells are perspective as new samples of electro-optical microsystems, including multi-channel SLMs. Additionally, two-wave mixing technique in such nonlinear cells may be successfully implemented in multi-channel couplers, switches, and optical communication lines. They may be also applied in networks, if to ensure the independent control of each channel in LCD structures.

Abreviaturas

5CB:: 4′-(n -pentyl)-4-cyanobiphenyl
E7:: Liquid crystal mixture
F1:: Hybrid LC cell, composed by flat part of Si plate 1/5CB/glass plate covered by ITO
F2:: Hybrid LC cell, composed by flat part of Si plate 2/5CB/glass plate covered by ITO
ITO:: Conductive layer of indium-tin-oxide
LC:: Liquid crystals
M1:: Hybrid LC cell, composed by microstructured part of Si plate 1/5CB/glass plate covered by ITO
M2:: Hybrid LC cell, composed by microstructured part of Si plate 2/5CB/glass plate covered by ITO
M3:: Hybrid LC cell, composed by microstructured part of Si plate 3/5CB/glass plate covered by ITO
M4:: Hybrid LC cell, composed by microstructured part of Si plate 4/E7/glass plate covered by ITO
Si:: Silicon

Detección de excitación espacialmente localizada en superredes de puntos cuánticos autoorganizadas InAs / InGaAs:una forma de mejorar la eficiencia fotovoltaica Supercondensadores lineales de alta velocidad y estirables miniaturizados

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias