Efecto de la morfología y la estructura cristalina en la conductividad térmica de los nanotubos de titania
Resumen
Los nanotubos de titania (TNT) con diferente morfología y estructura cristalina se preparan mediante procesos químicos y métodos de anodización de descomposición rápida (RBA). Los nanotubos se estudian en términos de conductividad térmica. Los TNT con espesor de pared variable por debajo de 30 nm tienen una conductividad térmica significativamente reducida que la titania a granel, debido al confinamiento del fonón, la trayectoria libre media del fonón más pequeña y la dispersión mejorada del límite del fonón. Los nanotubos amorfos (TNT Amor ) tienen paredes comparativamente más gruesas que ambos nanotubos cristalinos. El Amor de TNT tiene una conductividad térmica de 0,98 W m −1 K −1 , que es ligeramente menor que la conductividad térmica de los nanotubos de anatasa cristalinos (TNT A ; 1,07 W m −1 K −1 ). Sin embargo, los nanotubos de titania con estructura mixta (TNT A, T ) y las dimensiones más pequeñas tienen la conductividad térmica más baja de 0,75 W m −1 K −1 , probablemente debido al confinamiento del fonón. Los resultados experimentales se comparan con el estudio teórico considerando el efecto de confinamiento de tamaño con diferentes dimensiones de pared de TNT y dispersión superficial. Los resultados concuerdan bien con el factor de rugosidad superficial ( p ) de 0,26 para TNT A, T , 0,18 para TNT A y 0,65 para TNT Amor , lo que indica una dispersión difusiva de fonones y superficies más rugosas para TNT A . Curiosamente, los presentes resultados junto con los presentados en la literatura sugieren que la reducción de la conductividad térmica con respecto al espesor de la pared ocurre también para los nanotubos amorfos. Esto se atribuye al papel de los propagones en el transporte térmico de estructuras desordenadas.
Antecedentes
Debido a la miniaturización persistente de los dispositivos electrónicos y sistemas nanoelectromecánicos (NEMS), el estudio de las nanoestructuras y sus propiedades ha atraído mucha atención en los últimos años [1, 2]. Los estudios sobre el control del tamaño y la nucleación de nanoestructuras se han presentado anteriormente, ya que las nanoestructuras se han utilizado para diferentes aplicaciones potenciales [3, 4]. La investigación sobre el control de las propiedades térmicas en nanoestructuras controlando el tamaño, la composición y la estructura es de particular interés debido a sus aplicaciones en la industria electrónica, NEMS y termoeléctrica avanzada [2, 5, 6]. Un caso particular es minimizar la disipación de calor en los circuitos integrados (CI) para su estabilidad y larga vida útil.
Los materiales unidimensionales (1D), como los nanotubos de carbono (CNT), poseen una conductividad térmica a temperatura ambiente de 3000 W m −1 K −1 , que es mucho más alta que la de un cristal de diamante [2, 5]. El CNT es una hoja de grafeno enrollada sin costuras y tiene una conductividad térmica más alta debido al fuerte enlace carbono-carbono y no tiene defectos puntuales ni límites [6]. A diferencia de la CNT, otros semiconductores cristalinos unidimensionales han reducido significativamente el transporte térmico en comparación con el material a granel [6]. Esta disminución en la conductividad térmica en las nanoestructuras de baja dimensión se atribuye a la reducción en la trayectoria libre media de fonones (MFP), tamaño de grano pequeño, dispersión del límite de fonones, rugosidad y defectos puntuales [6,7,8].
Se han estudiado los nanocables de silicio para adaptar el transporte térmico para su utilización en aplicaciones termoeléctricas. Por primera vez, Li et al. [9] informó de conductividades térmicas dos veces más bajas para los nanocables de silicio en comparación con el silicio a granel debido a la dispersión en los límites de los fonones. La conductividad térmica de los nanocables de silicio con un diámetro de 50 nm se acercó al límite amorfo del silicio, con una reducción de 100 veces de la conductividad térmica en comparación con el silicio a granel [10]. Estos nanocables de silicio con conductividad térmica considerablemente reducida y conductividad eléctrica aumentada poseen una mayor eficiencia termoeléctrica [10,11,12,13]. También se informan las propiedades térmicas reducidas de otros nanocables en comparación con sus materiales a granel, como Bi 2 Te 3 [14, 15], Si / SiGe [16], Ge / SiGe [17, 18], ZnTe [19], GaN [20], InSb [21], CdS [22], PbS, PbSe [23], InAs [24], Bi [25], SrTiO 3 [26], ZnO [27] y TiO 2 nanocables [28, 29]. Además, los estudios térmicos en nanotubos como Si [30], Bi 2 Te 3 [31] y TiO 2 nanotubos [1, 32,33,34]. Con base en estos estudios, se puede concluir que la conductividad térmica de los nanotubos es menor que la de los nanocables correspondientes debido a la dispersión adicional de fonones dentro de las paredes de los nanotubos [31]. Cabe señalar que la conductividad térmica de los nanotubos cristalinos generalmente es más alta que la de sus homólogos amorfos y está fuertemente influenciada por la rugosidad de su superficie [32, 34]. Además, Wingert et al. [30] notó que los nanotubos de silicio cristalino tienen una conductividad térmica más baja que sus equivalentes amorfos. Esta observación de la conductividad térmica más allá del límite amorfo en los nanotubos de silicio cristalino se atribuyó al reblandecimiento elástico y la fuerte dispersión del límite fonónico [30]. El transporte térmico en los nanomateriales amorfos se atribuye principalmente (93%) a los difusores (modos de "difusión" no propagables), mientras que el 4% restante está relacionado con modos similares a fonones conocidos como "propagones" y el 3% a los modos localizados. conocido como "locons" [35]. Dado que normalmente se considera que el camino libre medio de los difusores es el de la distancia interatómica, se espera que la conductividad térmica de las nanoestructuras amorfas sea independiente de las dimensiones [36].
Cahill y Pohl propusieron un conocido modelo de conductividad térmica mínima para los materiales desordenados [37]. Según ese modelo, la conductividad térmica mínima propuesta (límite amorfo) de la titania es 1,6 W m −1 K −1 [38]. No se ha informado de una reducción dependiente del tamaño de la conductividad térmica de los óxidos amorfos [35], aunque se ha afirmado que algunas películas de óxido tienen una conductividad térmica por debajo del límite amorfo. La razón del menor valor de conductividad térmica obtenido se atribuyó a las impurezas en la estructura o, en el caso de películas delgadas, a la resistencia límite térmica entre la película y el sustrato [35].
Los nanotubos de titania, nanoestructuras 1D con una gran superficie específica, se han diseñado para varias aplicaciones potenciales [39]. Los nanotubos de titania pueden sintetizarse mediante varios métodos, incluidos anodización hidrotermal [40] y electroquímica [39, 40], procesamiento químico [41], anodización de descomposición rápida (RBA) [42] y métodos asistidos por molde y electrohilado [40]. Conductividad térmica en el rango de 0,40 a 0,84 W m −1 K −1 [1] y 0,55–0,75 W m −1 K −1 [33] se han observado para los nanotubos de titanato sintetizados por el proceso hidrotermal. Brahmi y col. [32] informó una conductividad térmica de 0,85 W m −1 K −1 para un único nanotubo amorfo y 1,5 W m −1 K −1 para nanotubos de titania anatasa preparados por anodización electroquímica. Por otro lado, se informó que las matrices de nanotubos de titania desprendidas tenían una conductividad térmica de 0,617 W m −1 K −1 a lo largo de la dirección del tubo para amorfo y 1,12 W m −1 K −1 para nanotubos de anatasa [34]. La conductividad térmica amorfa del tubo transversal fue de 0.077–0.1024 W m −1 K −1 para nanotubos amorfos y 0,24 W m −1 K −1 en el caso de nanotubos cristalinos [34]. Las matrices de nanotubos de titania en estos informes se cultivan en sustrato de Ti mediante el método de anodización electroquímica utilizando electrolitos orgánicos con iones de fluoruro (tercera generación de TNT) con un espesor de pared de 30-70 nm [32] y 15 nm [34]. Los nanotubos preparados por RBA forman parte de la cuarta generación de TNT [43], donde se obtienen haces de nanotubos de titania utilizando un electrolito libre de fluoruro [42].
En la presente contribución, presentamos un estudio experimental comparativo sobre la conductividad térmica de nanotubos de titania con morfología variable, estructura cristalina y un espesor de pared por debajo de 30 nm. Los nanotubos se sintetizan mediante procesamiento químico [41] y RBA [42]. La investigación de la conductividad térmica se extiende a la cuarta generación de nanotubos de titania (es decir, polvos preparados por RBA) y a la comparación de polvos de TNT mediante diferentes métodos de síntesis. Liang y Li [44] propusieron un modelo analítico de conductividad térmica dependiente del tamaño para nanomateriales, que se confirmó experimentalmente para nanocables y películas. El modelo fue posteriormente modificado por Gao y Jelle [1] para nanotubos, pero no ha sido verificado experimentalmente. Según el modelo, la conductividad térmica de los nanotubos depende del espesor de la pared [1]. Brahmi y col. [32] estudiaron la conductividad térmica de los TNT con un espesor de pared variable de 30 a 70 nm; sin embargo, en su estudio no se observó una reducción de la conductividad térmica con el espesor de la pared. En el presente informe, verificamos experimentalmente la conductividad térmica dependiente del tamaño de los nanotubos de titania mediante la reducción de las dimensiones de la pared en los nanotubos de titania cristalinos. Contrariamente a la percepción general, los datos actuales combinados con los presentados en la literatura sugieren una reducción dependiente del tamaño de la conductividad térmica también para los nanotubos de titania amorfos.
Métodos / Experimental
Síntesis de TNT
Los polvos de nanotubos de titanio (TNT) se prepararon utilizando métodos de procesamiento químico y anodización de descomposición rápida (RBA), como se describe en detalle en [41, 42], respectivamente. Se prepararon tres tipos de nanotubos de titania con diferente estructura cristalina y morfología, es decir, (i) TNT multipared de extremos abiertos, (ii) TNT amorfos de pared simple con un extremo abierto y el otro cerrado, y (iii) nanotubos de titania cristalinos con un extremo abierto y el otro cerrado. Los nanotubos de titania de extremos abiertos de paredes múltiples se prepararon mediante el método de procesamiento químico y tenían una estructura cristalina mixta de titanato (Na x H 2 - x Ti 3 O 7 · NH 2 O, donde 0 < x <2) con picos prominentes de la fase anatasa [41] y denominada TNT A, T a lo largo del texto. Se prepararon otros dos tipos de nanotubos mediante el método RBA utilizando un electrolito a base de agua (ácido perclórico 0,1 M) para obtener TNT cristalinos con estructura de anatasa o un electrolito orgánico (etilenglicol + agua + ácido perclórico) para producir nanotubos amorfos [42] . El amorfo (TNT Amor ) y cristalino (TNT A ) Los polvos de nanotubos de titania producidos por RBA son de pared simple con un extremo abierto y el otro cerrado. La ilustración esquemática de estos TNT se muestra en la Fig. 1.
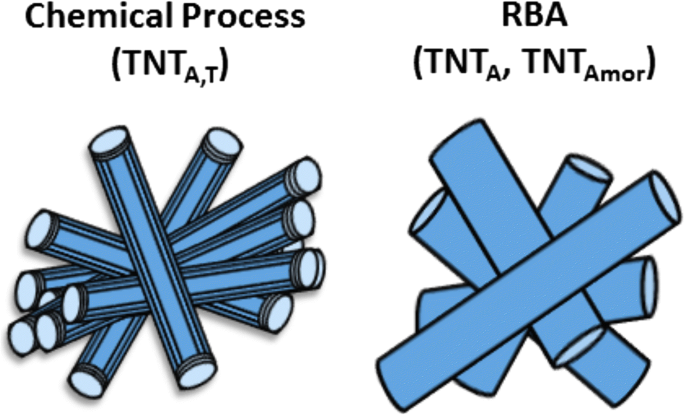
Ilustración esquemática de TNT A, T , TNT A y TNT Amor
Métodos de caracterización
La morfología y el tamaño de los polvos de nanotubos de titania se examinaron mediante microscopía electrónica de transmisión (TEM; Tecnai F-20 G2 200 kV FEG S-twin GIF) a una tensión de funcionamiento de 200 kV. La estructura cristalina se obtuvo mediante difracción de rayos X (XRD). Los datos de XRD se obtuvieron utilizando un difractómetro PANalytical X'pert Pro. La longitud de onda operativa fue de radiación Cu-Kα de 0,154 nm, con voltaje y corrientes de 40 kV y 45 mA, respectivamente. La densidad de cada polvo se midió con un picnómetro (Upyc 1200e v5.04; Quantachrome Corporation). A continuación, los polvos se comprimieron en gránulos de 10 mm para medir la conductividad térmica. Los gránulos se fabricaron mediante prensado hidrostático de nanotubos en polvo y el espesor de los gránulos obtenidos estuvo en el rango de 2 a 4 mm. El espesor medido y la densidad calculada de los gránulos están relacionados con la presión aplicada, que se controló en un rango de 5 a 50 kN para ajustar la densidad de cada gránulo. Las superficies de los gránulos se analizaron mediante un microscopio electrónico de barrido con pistola de emisión de campo (FEG-SEM; Hitachi S-4700).
La difusividad térmica de los gránulos se midió usando el método de flash de luz utilizando equipo Netzsch LFA 467 con software Proteus LFA a temperatura ambiente. Un pulso de láser de xenón de luz corta calentó la superficie trasera de los perdigones. Antes de las mediciones, los gránulos se recubrieron con un spray de grafito para mejorar la absorción y emisión de la radiación térmica. Un detector de infrarrojos observó el cambio de temperatura correspondiente en el lado opuesto del gránulo. Según Parker et al. [45], se puede utilizar la siguiente relación para obtener la difusividad térmica a partir de los datos experimentales:
$$ \ alpha =\ frac {0.1338 \ {d} ^ 2} {t ^ {1/2}} $$ (1)Aquí, α es la difusividad térmica de la muestra, d es el grosor de la muestra y t 1/2 es el valor de tiempo a la mitad de la altura de la señal. Las mediciones de LFA se repitieron cinco veces por muestra. Se utilizó el software Proteus para ajustar las medidas. La conductividad térmica de la muestra se obtuvo utilizando la siguiente relación [45]:
$$ \ kappa (T) =\ alpha (T) \ {c} _p (T) \ \ rho (T) $$ (2)Aquí, κ denota la conductividad térmica, α denota la difusividad térmica, c p es la capacidad calorífica específica, y ρ es el valor de la densidad. La capacidad calorífica específica de los nanotubos de titania se aproxima a la del dióxido de titanio a granel por encima de 100 K [46] y, por lo tanto, los valores de la capacidad calorífica específica para los nanotubos de titania se adoptaron de un estudio de Guo et al. [34, 47]. La densidad de los gránulos se calculó a partir del peso y el volumen correspondiente de los gránulos. La incertidumbre en los resultados experimentales proviene de los errores de la unidad de medida LFA para las medidas de difusividad (2%) y el cálculo del espesor de los gránulos por un micrómetro. El error total de los experimentos de conductividad térmica se estimó en un 8%.
Resultados y discusión
Los datos XRD para la estructura cristalina de los nanotubos se muestran en la Fig. 2. El TNT Amor los datos no tienen picos que confirmen la estructura amorfa de los nanotubos preparados por RBA utilizando un electrolito orgánico [42]. Los nanotubos procesados químicamente (TNT A, T ) muestran picos prominentes de la fase anatasa junto con H 2 Ti 3 O 7 picos. La estructura distinta de la anatasa se asignó como Na x H 2 - x Ti 3 O 7 · NH 2 O donde 0 < x <2, como se informó en un estudio anterior [41]. El TNT A preparados por electrolitos a base de agua tienen picos de anatasa. A partir de los datos de XRD, es obvio que dos tipos de nanotubos son cristalinos y uno es amorfo.
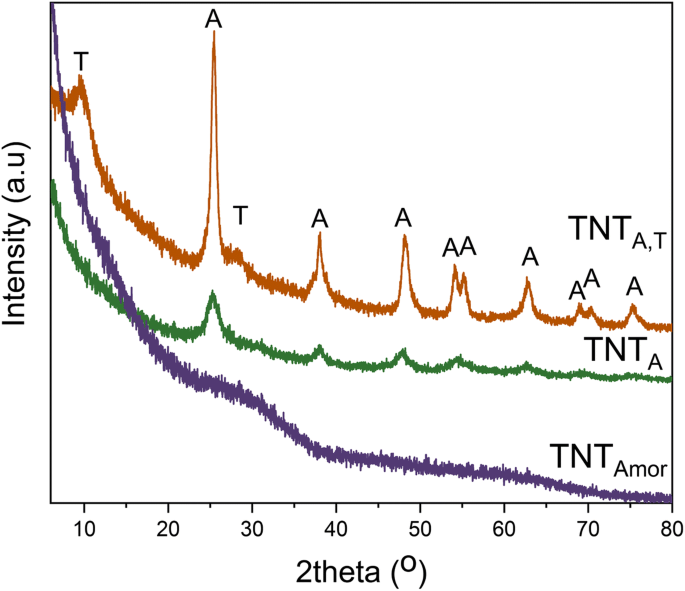
XRD de nanotubos de titania cristalinos que consisten en anatasa (TNT A ), tanto titanato como anatasa (TNT A, T ) y estructura amorfa (TNT Amor ) [41, 42]. T =H 2 Ti 3 O 7 , A =picos de anatasa
Los nanotubos de titania sintetizados por el método de procesamiento químico son de paredes múltiples debido al desplazamiento de las nanohojas durante la síntesis de nanotubos [48]. Estos nanotubos abiertos tienen un espesor de pared de 4-5 nm con una longitud variable de 60 a cientos de nanómetros [41]. Las imágenes TEM de estos nanotubos se muestran en la Fig. 3a, b. Los nanotubos están orientados aleatoriamente y prefieren permanecer en paquetes como se muestra en la Fig. 3a. La estructura de paredes múltiples de 3 a 4 capas es evidente como se muestra en la Fig. 3b. Los nanotubos cristalinos producidos por RBA tienen un espesor de pared en el rango de 7 a 12 nm y una longitud de 18 a 35 μm [42] (Tabla 1). Son de pared simple con un extremo abierto y el otro cerrado, como se muestra en la micrografía de la Fig. 3c, donde el recuadro muestra el extremo abierto. Los nanotubos amorfos producidos por RBA tienen una morfología similar a los nanotubos cristalinos preparados por el método RBA. Sin embargo, las dimensiones son diferentes debido al aporte del electrolito. El espesor de la pared está en el rango de 15 a 30 nm y la longitud tubular está en el rango de 6 a 13 μm [42]. La Figura 3d muestra la imagen TEM del nanotubo amorfo de pared simple. La rugosidad es el valor medio de la desviación de la altura de la superficie de la pared TNT del plano de referencia [44]. Los valores de rugosidad promedio estimados a partir de imágenes TEM de los TNT son aproximadamente 0,3 nm para TNT A, T , 1.0 nm para TNT A y 1,5 nm para TNT Amor .

Imágenes TEM de a el TNT A, T preparado mediante procesamiento químico, b Micrografía HR-TEM que muestra la estructura de nanotubos de paredes múltiples, c los nanotubos cristalinos de pared simple preparados (TNT A ) por RBA y d los nanotubos amorfos (TNT Amor )
Los gránulos de nanotubos de titania se prepararon en diferentes densidades y porosidades correspondientes utilizando una prensa hidráulica. TNT Amor El polvo se compactaba con una carga máxima de 20 kN porque a cargas más altas no se obtenía la superficie lisa de los gránulos necesarios para las mediciones de LFA. La porosidad de los gránulos se calcula de la siguiente manera (Ec. 1):
$$ P =\ frac {\ rho_o- \ rho} {\ rho_o} $$ (3)donde ρ o es la densidad de las muestras a granel, que es la densidad del polvo obtenida por las mediciones del picnómetro y que se muestra en la Tabla 1. La ρ es la densidad calculada del gránulo y P es la porosidad de las muestras. Las superficies de los gránulos se estudiaron con FESEM en el archivo adicional 1. Los análisis de las superficies muestran la orientación aleatoria de los haces de nanotubos (archivo adicional 1:Figura S1) en la superficie, es decir, los nanotubos se pueden observar en varias orientaciones (parte superior abierta, posición inferior cerrada y vista lateral) en el archivo adicional 1:Figura S1. Imágenes SEM similares de superficies de pellets de TNT A , TNT Amor y TNT A, T los gránulos se muestran en el archivo adicional 1:Figura S2a – c. La difusividad térmica medida por el método LFA se resume en la Tabla 2. Las conductividades térmicas medidas se representan en función de la porosidad, como se muestra en la Fig. 4. La conductividad térmica medida disminuye al aumentar la porosidad para todas las muestras (Tabla 2). Gao y Jelle obtuvieron una tendencia similar para los valores de conductividad térmica de muestras con diferentes porosidades de pellets [1]. Se obtiene una clara reducción de la conductividad térmica de los nanotubos en comparación con la titania a granel (8,5 W m −1 K −1 [34]). Esta supresión de la conductividad térmica en los nanotubos de titania 1D se atribuye al confinamiento del fonón y a la dispersión del límite del fonón debido a la reducción de tamaño [1]. Como los nanotubos están orientados y compactados aleatoriamente para formar gránulos, también están conectados entre sí. En este caso, la dispersión de fonones en el área interconectada entre los nanotubos y la resistencia de Kapitza también afecta los valores generales de conductividad térmica. Sin embargo, la resistencia de contacto de Kapitza y la dispersión del límite de fonón considerando la orientación de los nanotubos se ignoran aquí por simplicidad.
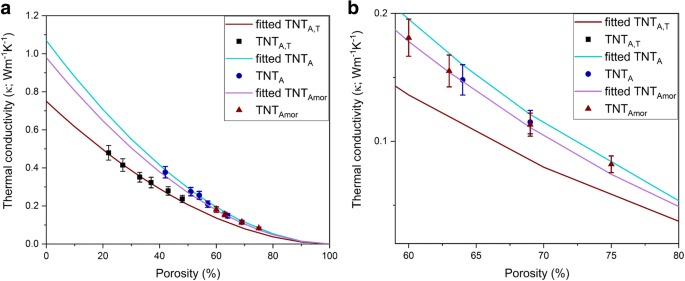
un Conductividad térmica efectiva medida de los nanotubos de titania (símbolos) frente a la porosidad. Las líneas continuas representan el ajuste usando el modelo de conductividad térmica efectiva (Ec. 6) con un factor de forma de 1.24. b Conductividad térmica en el rango de porosidad del 60 al 80% para mayor claridad
La conductividad térmica medida de una muestra estima la conductividad de los gránulos de nanotubos considerando tanto los nanotubos de titania como los poros llenos de aire. Se supone que la conductividad térmica del aire es de 0,026 W m −1 K −1 [1]. La conductividad térmica de los nanotubos ( κ TNT ) excluyendo el impacto de la porosidad se puede estimar utilizando modelos de conductividad térmica efectivos dados por la Ec. 4 [1, 49], que para el caso de poros no conductores se reduce a Eq. 5 [1]:
$$ {\ kappa} _ {TNTs} =\ frac {\ upkappa_ {eff} - {\ upkappa} _ {air} \ cdot P} {\ left (1-P \ right)} $$ (4) $$ {\ kappa} _ {TNTs} =\ frac {\ upkappa_ {eff}} {\ left (1-P \ right) \ kern0.5em} $$ (5)donde κ ef es la conductividad térmica efectiva que incluye el efecto de porosidad, κ aire es la conductividad térmica del aire y P es la porosidad. La conductividad térmica de TNT A, T estimado a partir de la ecuación. 4 está en el rango de 0,44 a 0,61 W m −1 K −1 para TNT A, T . Utilizando el modelo de conductividad térmica efectiva (ecuación 4), se ha informado que la conductividad térmica de nanotubos de titanato puro con dimensiones aproximadamente similares es de 0,40 a 0,84 W m −1 K −1 [1]. Nuestros resultados concuerdan bien con los valores reportados cuando se usa el mismo modelo efectivo de conductividad térmica (Ec. 4).
Sin embargo, la forma de los espacios de aire en los nanotubos compactos es solo parcialmente aleatoria, ya que los propios tubos tienen una forma no aleatoria. Para tener en cuenta las diferentes formas de los poros, Bauer [49] derivó un modelo analítico aplicable para una gama completa de porosidades basado en la resolución de la ecuación de conducción de calor de Laplace. Esta ecuación se puede presentar de la siguiente forma:
$$ \ frac {\ kappa_ {eff}} {\ kappa_ {TNTs}} ={\ left (1-P \ right)} ^ {\ frac {3 \ varepsilon} {2}} $$ (6)En esta ecuación, ε es el factor de forma o factor de corrección relacionado con la forma de los poros. Su valor explica las formas variables de los poros. Para formas aleatorias del espacio de aire, ε es 2/3 [1, 27, 50] reduciendo así la ecuación. 5 a la ecuación. 6.
Los valores de los factores de forma han sido estimados para formas poliédricas por Yang et al. [50], basado en factores de forma de modelado entre 1 y 1,48. Al ajustar nuestros datos a la ecuación. 6, el mejor ajuste (ver Fig. 4) se obtiene para el factor de forma ε que tiene el valor de 1,24. Según el ajuste, la conductividad térmica para TNT A resulta ser 1.07 W m −1 K −1 . Este valor es algo más bajo que los valores reportados anteriormente, 1.12 W m −1 K −1 para matrices de nanotubos anatasa [34] y 1,5 W m - 1 K - 1 para un solo nanotubo de anatasa [32]. En consecuencia, la conductividad térmica de TNT Amor resulta ser 0,98 W m −1 K −1 . El valor ligeramente más bajo de conductividad térmica en los nanotubos amorfos en comparación con TNT A se atribuye a su estructura amorfa. En [32, 34] también se han informado valores de conductividad térmica más bajos de los nanotubos de titania amorfos que los de los nanotubos cristalinos. Generalmente, se sabe que las películas y materiales amorfos tienen una conductividad térmica más baja en comparación con los materiales cristalinos, aunque a una escala tan pequeña, otros factores también influyen en los valores de conductividad térmica. Por ejemplo, Wingert et al. [30] informó de una conductividad térmica un 30% más baja para los nanotubos de silicio cristalino en comparación con sus homólogos amorfos con dimensiones similares. La conductividad térmica sub-amorfa de esos nanotubos se atribuyó al fuerte efecto de ablandamiento elástico en los nanotubos cristalinos [30]. En comparación con las películas amorfas, la conductividad térmica medida de la película de titania amorfa de 100 nm depositada mediante el proceso ALD fue de 1,29 W m −1 K −1 [47]. La conductividad térmica aproximada por el modelo de Cahill y Pohl de la conductividad térmica mínima [37] fue 1,38 W m −1 K −1 para la misma película [47]. Se informó que la conductividad térmica de las películas de titania amorfa depositadas por pulverización catódica es de 1,6 W m −1 K −1 para películas de 920 nm de espesor [38, 51]. La conductividad térmica obtenida para los nanotubos es menor que la de las películas de titania amorfa tratadas en estos informes [38, 47, 51]. Sin embargo, conductividad térmica comparativamente más baja de 0,7 W m −1 K −1 [52] también se informó para una película de titania amorfa de 150 nm de espesor preparada por pulverización catódica y 0,9 W m −1 K −1 [53] para una película de 120 nm de espesor preparada mediante el método sol-gel. En el caso de las películas, se consideró que la resistencia límite térmica entre el sustrato, la película delgada y la película metálica del transductor reducía la conductividad térmica general por debajo del límite amorfo [52]. En el caso de los nanotubos, factores como la resistencia al contacto térmico entre los nanotubos, la rugosidad de la superficie y las impurezas en la estructura debido al proceso de preparación también afectan la conductividad térmica neta. Guo y col. [34] propuso el valor más alto de resistencia al contacto térmico entre matrices de nanotubos amorfos en comparación con los nanotubos cristalinos. Conductividad térmica de 0,85 W m −1 K −1 se ha informado para un solo nanotubo amorfo [32], mientras que Guo et al. [34] informó la conductividad térmica de 0,617 W m −1 K −1 para matrices de nanotubos amorfos a lo largo de la dirección del tubo. Para TNT A, T , conductividad térmica de 0,75 W m −1 K −1 es obtenido. Este valor concuerda bien con los resultados publicados para nanotubos de titanato [1, 33] preparados por método hidrotermal. También se observa que la conductividad térmica aumenta con la densidad creciente del material que se muestra en la Tabla 1. La densidad medida de TNT A (3,79 g cm −3 ) está cerca de la densidad aparente de anatasa de 3,89 g cm −3 [34]. La densidad de TNT A, T también se correlaciona bien con la densidad medida de titanato mixto y nanoestructura compactos de titania [54]. El Amor de TNT tiene una densidad de 3,67 g cm −3 , que se acerca a la densidad informada de la película de titania amorfa (3,73 g cm −3 ) depositado por ALD [55]. La dependencia lineal de la conductividad térmica con la densidad ya se informó para las películas de alúmina antes [55].
El camino libre medio de fonones se ha calculado como 2,5 nm para titania [1], 1,21-3,15 nm para nanofibras de titania [28] y 2-3 nm para nanotubos de titania [32]. De los tres tipos diferentes de nanotubos estudiados en el presente informe, los nanotubos anatasa (TNT A ) producen el valor de conductividad térmica más alto, mientras que la conductividad térmica de TNT A, T de paredes múltiples es menor que el de TNT A y TNT Amor . En la Fig. 5 se muestra una comparación de los valores de conductividad térmica presentes y publicados anteriormente con respecto al espesor de pared de los TNT. Los TNT producidos a partir del método hidrotermal, [1, 33] matrices anodizadas de tercera generación [34] y nanotubos simples [ 32], y los valores de los nanotubos producidos por el presente RBA y los métodos de procesamiento químico se grafican con sus valores promedio de espesor de pared y conductividades térmicas (Fig. 5). La Figura 5 muestra que la conductividad térmica de los nanotubos de titania cristalinos se reduce significativamente al reducir el espesor de la pared. La supresión de la conductividad térmica con la reducción del espesor de la pared se atribuye al confinamiento del fonón con el espesor de la pared [32]. Aunque este efecto no fue observado por Brahmi et al. [32], obviamente debido a la limitación de muestras con dimensiones reducidas, la reducción propuesta se observa con el presente TNT A, T . La Figura 5 muestra una tendencia similar para los nanotubos amorfos con la reducción de la conductividad térmica con el espesor de la pared. Generalmente, se espera que los nanomateriales amorfos tengan una conductividad térmica similar independientemente de la escala, ya que el transporte térmico se atribuye a los difusores que no se propagan [47]. Dependiendo del material y sus dimensiones, los propagones (propagación de vibraciones) también pueden contribuir a la conductividad térmica global [35]. Wingert y col. [35] propuso la reducción de la conductividad térmica para las películas de silicio amorfo reduciendo el espesor de la película de un rango de micrómetros a nanómetros. Más tarde, la reducción de la conductividad térmica dependiente del tamaño para el silicio amorfo ha sido confirmada experimentalmente por Kwon et al. [36] debido a la contribución de los propagones en el transporte térmico general. Se encontró que el camino libre medio de los propagones para el silicio amorfo estaba en el rango de 10 nm a 10 µm y contribuyeron a un aumento del 30% en la conductividad térmica a temperatura ambiente [36]. Se ha estimado que el camino libre medio de la titania amorfa está en el rango de 0,195 a 0,201 nm (distancia interatómica ≈) [56]. No se encuentra ningún estudio que indique la trayectoria libre media de los propagones en titania. Sin embargo, la reducción de la conductividad térmica con la disminución del grosor de la pared también se observa para los TNT amorfos (Fig. 5). Por lo tanto, se especula que el transporte térmico en los TNT se atribuye no solo a los difusones, sino que los propagones también pueden contribuir a la conductividad térmica general, lo que reduce la conductividad térmica de los nanotubos amorfos al reducir las dimensiones de la pared.
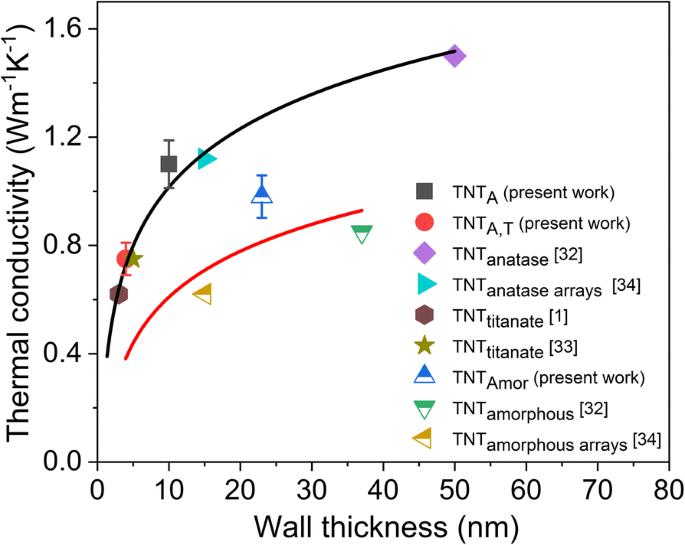
La conductividad térmica de nanotubos de titania amorfos y cristalinos con respecto a su espesor de pared. Las líneas de tendencia se agregan para una guía visual
Se ha propuesto que las propiedades térmicas de los nanotubos dependen de su espesor de pared más que del diámetro [1, 32]. Gao y Jelle presentaron una aproximación teórica para la reducción de la conductividad térmica con el espesor de la pared [1], que era una modificación de un modelo propuesto anteriormente [44]. Sin embargo, la conductividad térmica general también se vio afectada por la rugosidad de la superficie de los nanotubos. Liang and Li [44] proposed the analytic formula for thermal conductivity of semiconductor nanomaterial including size confinement effects, crystallinity length, and the surface scattering of phonons by the surface roughness parameter (p ) as follows:
$$ \frac{\kappa_{TNT}}{\kappa_B}=p\cdot \exp \left(-\frac{l_o}{L}\right)\cdot {\left[\exp \left(\frac{1-\alpha }{\frac{L}{L_o}-1}\right)\right]}^{3/2\operatorname{}} $$ (7)where κ TNT is the thermal conductivity of the nanomaterial, κ B is bulk thermal conductivity, l o is the phonon mean free path, L is the wall thickness, and L o is the critical size at which almost all atoms of a crystal are located on its surface [44]. It should be noted that L o = 2(3 − d )w , where d is the dimension of the material (which is 1 in the case of nanotubes) and w is the atomic or molecular diameter [1, 44]. Finally, α is a material constant = 2Sv /3R + 1, where Sv is the bulk vibrational entropy and R is the ideal gas constant [44]. The phonon mean free path of the titania nanotubes calculated from the kinetic formula of lattice thermal conductivity was reported to be 2.5 nm [1]. The bulk thermal conductivity of titania (κ B ) is 8.5 W m −1 K −1 as noted previously. The values for w , Sv , and α are obtained from the study by Gao and Jelle [1]. The surface roughness factor p obtains values from 0 to 1, where smaller value of p corresponds to a rougher surface and diffusive phonon scattering and larger values correspond to smooth surfaces with specular phonon scattering [1, 32, 44]. Figure 6a shows the thermal conductivities of crystalline nanotubes for different wall thicknesses and scattering factors. The p factor of 0.4 was found best for estimating the thermal conductivity of 2-nm rutile nanoparticles in [57] as well as for silicon nanowires having the diameter of 20–100 nm in [44]. The same p value of 0.4 has also been used for titanate nanotubes by Gao and Jelle [1], who theoretically estimated thermal conductivity values of TNTs between 0.30 and 0.77 W m −1 K −1 for 2–3-nm wall thickness. Contrary to the previous reports, by using Eq. 7 our experimental data for TNTA,T fit with the p factor of 0.26 as shown in Fig. 6a. The practical value is plotted at a maximum wall thickness. For TNTA , the thermal conductivity value obtained by using Eq. 7 at the maximum wall thickness (12 nm) fits with the calculated surface roughness factor of 0.18. These small values are associated with the rough surface of the anodized nanotubes. The p factor corresponds to p = 1 − 10η /L , where η is the surface roughness of nanotubes and L is the thickness of the material [44]. This equation gives the approximation of surface roughness of 0.22–0.29 nm for TNTA,T and 0.56–0.96 nm for TNTA . These values correlate quite well with the roughness values estimated from the TEM micrographs. The difference in surface roughness for both nanotubes results from the synthesis process. It is pointed out that the thermal conductivity increases with increasing wall thickness for both crystalline nanotubes. This provides experimental verification for the model proposed by Liang and Li [44] and modified for nanotubes by Gao and Jelle [1], where thermal conductivity increases with an increase in wall thickness. The decline in the wall dimensions leads to the reduced phonon mean free path by phonon confinement and increased diffuse phonon boundary scattering, resulting in overall reduction in thermal conductivity values [32]. The crystal defects as well should influence the net thermal conductivity value along with the thermal contact resistance between the nanotubes, which are not considered here. Equation 7 is also adapted for the amorphous nanotubes (TNTAmor ) and the maximum value of wall thickness (30 nm) is plotted in Fig. 6b. The bulk thermal conductivity (κ B ) of the titania is estimated as 1.6 W m −1 K −1 [38] from the minimum thermal conductivity model and l o is estimated as 0.198 nm [56]. The experimental value fits well with the p factor of 0.65 for amorphous nanotubes, which gives the surface roughness of 0.99–1.98 nm for the TNTAmor . The mean roughness of TNTAmor estimated from the TEM images (1.5 nm) fits well with this theoretical range. The surface roughness in one-dimensional crystalline nanostructures (< 100 nm) has a strong impact on the overall thermal conductivity reduction due to the diffusive phonon boundary scattering [58, 59]. In the case of amorphous material, the surface roughness could play a role if it approaches the wavelength of the propagons [36].
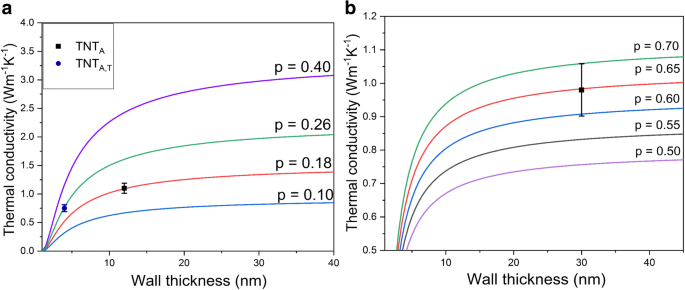
Size-dependent thermal conductivity of a crystalline titania nanotubes (TNTA and TNTA,T ) and b amorphous nanotubes (TNTAmor ) with different surface roughness factors; symbols show the experimental thermal conductivity of the studied titania nanotubes and the solid lines indicate the calculated thermal conductivities by using Eq. 6
Conclusiones
Three different kinds of titania nanotubes are synthesized with different crystal structure and morphology by using chemical processing and rapid breakdown anodization methods. Based on the measurement results at room temperature, the thermal conductivity of the titania nanotubes is considerably lower as compared to the bulk titania. Titania (TNTA ) nanotubes are single-walled with one end opened and other closed, and they have anatase structure and a wall thickness of 7–12 nm. The thermal conductivity of these nanotubes estimated by an effective model of thermal conductivity is 1.07 W m −1 K −1 . The amorphous nanotubes (TNTAmor ) with a wall thickness of 15–30 nm have a thermal conductivity of 0.98 W m −1 K −1 . Their thermal conductivity is slightly lower than that of crystalline anatase nanotubes (TNTA ). However, the multiwalled and open-ended nanotubes (TNTA,T ) with a mixed crystal structure and a wall thickness of 4–5 nm have the lowest thermal conductivity of 0.75 W m −1 K −1 . This low value of thermal conductivity is due to the reduced dimensions of walls approaching the calculated 2.5-nm phonon mean free path. The reduction in the wall thickness is found to result in overall suppression of the thermal conductivity as the phonon confinement is enhanced and the phonon boundary scattering increased. The size confinement effects of phonon transport with different surface-related parameters for both crystalline and amorphous nanotubes are considered. Generally, the thermal conductivity of amorphous oxides is found independent of the size. Comparison of the present result on the amorphous nanotubes with those in the literature, however, suggests also size-dependent reduction in the thermal conductivity of the amorphous nanotubes. This may be due to the possible contribution of propagons in the overall thermal transport in disordered structure along with the diffusons. For TNTA,T , the thermal conductivity value agrees well with the surface roughness factor of 0.26, while in the case of TNTA nanotubes, it matches with 0.18 confirming the different surface roughness of the two kinds of crystalline nanotubes related to the synthesis processes. TNTAmor surface roughness (1.5 nm) estimated from TEM micrographs is in line with the calculated surface roughness factor of 0.65.
Abreviaturas
- RBA:
-
Rapid breakdown anodization
- SEM:
-
Microscopía electrónica de barrido
- TEM:
-
Microscopía electrónica de transmisión
- TNTA :
-
Titania nanotubes with anatase crystal structure
- TNTA,T :
-
Titania nanotubes with mixed crystal structure (anatase and titanate)
- TNTAmor :
-
Titania nanotubes with amorphous structure
- TNTs:
-
Titania nanotubes
- XRD:
-
Difracción de rayos X
Nanomateriales
- Estructura cristalina y de valencia
- Presentación de la estructura atómica y electrónica de las nanofibras de carbono de copa apilada
- El efecto de los aniones sulfato en la nucleación de titania ultrafina
- Efecto de la distribución de nanopartículas de oro en TiO2 sobre las características ópticas y eléctricas de las células solares sensibilizadas por colorante
- El efecto del plasma de no equilibrio por contacto sobre las propiedades estructurales y magnéticas de Mn Х Fe3 - X О4 Espinelas
- Efecto del tratamiento de recocido in situ sobre la movilidad y morfología de transistores de efecto de campo orgánico basados en TIPS-pentaceno
- Efecto del polietilenglicol en el fotocátodo de NiO
- Influencia del agua en la estructura y propiedades dieléctricas de la microcristalina y nanocelulosa
- Morfología, estructura y propiedades ópticas de películas semiconductoras con nanoislinas GeSiSn y capas tensas
- Estudio comparativo de las propiedades electroquímicas, biomédicas y térmicas de nanomateriales naturales y sintéticos
- Reduzca la sensibilidad de CL-20 mejorando la conductividad térmica a través de nanomateriales de carbono



