Influencia del agua en la estructura y propiedades dieléctricas de la microcristalina y nanocelulosa
Resumen
Se estudió la influencia del agua en los diferentes estados sobre la estructura y las propiedades dieléctricas de la celulosa microcristalina mediante rayos X, termogravimetría y espectroscopía dieléctrica. En la investigación de celulosa microcristalina (MCC) con diferente contenido de agua, se muestra que las moléculas de agua se encuentran en los macroporos de MCC y en capas hidratadas multimoleculares. Se muestra que al aumentar la concentración de agua en una cáscara hidratada, se produce la reorganización de las moléculas de celulosa en la superficie de los cristalitos, y como resultado, aumenta su tamaño transversal y cristalinidad. Se muestra que durante la concentración de agua, aparece más del 13% en una capa hidratada continua de cristalitos. Se estudiaron las dependencias de temperatura de partes reales e imaginarias de permitividad dieléctrica compleja en el intervalo de temperaturas [−180 ÷ 120] ° C en frecuencias de f =5, 10, 20 y 50 kHz. Se observó un proceso de relajación a baja temperatura y una transición a alta temperatura. Proceso de relajación a baja temperatura que está relacionado con la transición de grupos metilol de superficie de moléculas de conformación de celulosa de tg a tt se desplaza hacia temperaturas bajas al aumentar la concentración de agua en la celulosa microcristalina.
Antecedentes
La celulosa habitual de diversas fuentes vegetativas, que es un recurso renovable ecológicamente limpio prácticamente inagotable, es una materia prima para la producción de celulosa microcristalina (MCC). Determina el creciente interés por la investigación de sus propiedades físicas y fisicoquímicas. Otro factor importante, que atrae la atención de los investigadores, es la disponibilidad de partículas cristalinas en la estructura del MCC, cuyo estudio de propiedades es prometedor para muchas direcciones de desarrollo de tecnologías modernas. Los más desarrollados a partir de estas direcciones son la industria farmacéutica y la cosmética [1]; sin embargo, en la actualidad, el MCC comienza a utilizarse como relleno en materiales compuestos [2], electrónica moderna [3] y óptica láser [4, 5]. En este sentido, la capacidad del MCC para absorber la humedad, que puede afectar sustancialmente sus propiedades, en particular, las estructurales [6], eléctricas [7, 8] y termofísicas [9, 10], es importante.
Métodos
Las muestras
Las muestras de grado MCC (Cellets-100), producidas por Shin-Etsu Company (Japón), se utilizaron para la investigación. El MCC inicial se dispersó en un mortero de ágata. Para obtener muestras libres de agua, las muestras se mantuvieron en la caja de secado durante 3 días a una temperatura de 115 ° C, y luego se encapsularon en el molde de prensado al vacío. Las muestras con diferente nivel de humedad se obtuvieron manteniéndolas en diferentes momentos en vapor de agua saturado.
Equipo
El análisis de la estructura de la muestra se realizó mediante el difractómetro de rayos X DRON-3M con el tubo BSV-28 ( λ =1,54178 Å).
El análisis térmico diferencial (DTA) y las investigaciones termogravimétricas se realizaron utilizando el derivatógrafo Q-1500D. Las investigaciones se llevaron a cabo dentro del rango de temperatura T =20 ÷ 250 ° con una velocidad de 5 ° C / min.
Las muestras para investigaciones dieléctricas se obtuvieron mediante la compactación de polvo de MCC entre recubrimientos de un acero inoxidable a la presión de 120 kg / cm 2 . Luego, la muestra con revestimientos laminados se colocó en la celda de cuatro electrodos termoestabilizados, lo que permitió controlar el espesor de la muestra durante las mediciones utilizando un condensador dieléctrico de aire adicional. Mediciones de la capacidad y el factor de pérdida de esta celda en cuatro frecuencias diferentes f =5, 10, 20, 50 kHz dentro del rango de temperatura (−180 ÷ 120) ° C se realizaron mediante instalación automatizada basada en el puente de corriente alterna P5083 [11].
Resultados y discusión
Investigaciones termogravimétricas
Las investigaciones de la cantidad de agua en MCC se realizaron usando el derivatógrafo Q-1500D. En la muestra investigada, la temperatura ( T ), cambio masivo ( m ) y la tasa de cambio de masa ( dm / dT ) se midieron simultáneamente y se realizaron análisis diferenciales y térmicos (DTA).
Dependencias de temperatura del cambio de masa relativo Δm / m 0 = ( m − m 0 ) / m 0 , m 0 –– masa de muestra inicial (ver Fig. 1) y derivada del cambio de masa dm / dT (ver Fig. 2).
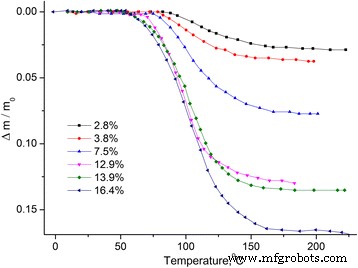
Dependencia de la temperatura del cambio de masa relativo de MCC. Dependencia de la temperatura del cambio de masa relativo Δ m / m 0 de muestras de MCC con diferente contenido de agua
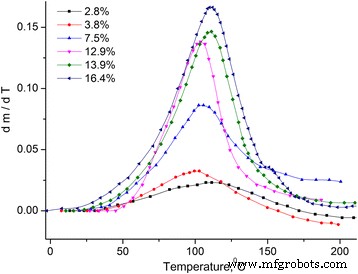
Dependencia de la temperatura de la derivada del cambio de masa de MCC. Dependencia de la temperatura de la derivada del cambio de masa dm / dT de muestras de MCC con diferente contenido de agua
Se puede considerar que la pérdida de masa de la muestra se debe a la evaporación del agua, que se encuentra en la muestra en diferentes estados [12, 13]. Por lo tanto, el dm / dT se dividió en picos utilizando la distribución de Gauss (ver Fig. 3).
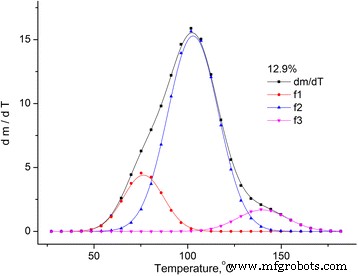
Aproximación del dm / dT dependencia para la muestra de MCC con la humedad del 12,9%. Aproximación del dm / dT dependencia para la muestra de MCC con la humedad del 12,9% utilizando la distribución de Gauss con tres picos
La dependencia de dm / dT para cada una de las muestras investigadas puede describirse mediante la superposición de tres picos. El primer pico ( f 1 ) está relacionado con la evaporación del agua de enlace físico-mecánico con MCC, que se ubica en los microporos de la muestra, el segundo ( f 2 ) es causado por el agua de las capas de hidratos polimoleculares y monomoleculares, y el tercer pico es causado por la degradación oxidativa térmica de la muestra.
En la Tabla 1, porcentaje S 1 en el cuadrado del pico general dm / dT y porcentaje de masa w i = CS i / 100% en masa general de diferentes tipos de agua y se muestra la destrucción de las muestras de MCC con diferente contenido de agua .
Se ve que la cantidad de agua ligada físicamente mecánicamente S 1 aumenta con el crecimiento del contenido de agua en general y la cantidad de agua en las conchas hidratadas S 2 también aumenta y alcanza su saturación a la concentración del agua general del 12,9%.
Consideremos con más detalle el segundo pico ( f 2 ), que es causada por la deshidratación de los cristales de celulosa.
El método para calcular los parámetros cinéticos del proceso de deshidratación, como la energía de activación E y factor preexponencial ( k 0 ) se describen en [12]. La ecuación cinética del proceso de desorción se puede presentar como:
$$ \ frac {dQ} {dt} =- k {Q} ^ n, k =\ frac {-dQ / dt} {Q ^ n}. $$ (1)Un grado de recubrimiento de los cristalitos de celulosa por las moléculas de agua ( Q ) cambia de 1 (para el material inicial) a 0 (el agua completa se deshidrata). Un orden de reacción ( n ) es un número entero de 1 a 3; se supone que se conoce por el experimento. La constante de la velocidad de reacción ( k ) se puede escribir como:
$$ k ={k} _0 \ exp \ left (- \ frac {E} {RT} \ right), $$ (2)donde R es constante de gas universal. El valor de E se toma en esta aproximación como una constante, lo que significa una equivalencia de todos los centros de hidratación de la superficie de los cristales de MCC. El factor preexponencial se puede escribir como k 0 =ZP , donde Z es el número teórico de discontinuidades de enlaces de hidrógeno entre moléculas de agua y celulosa (MCC) en una capa de hidrato por unidad de tiempo, y P es un factor de probabilidad que tiene en cuenta todos los efectos causados por una desviación de la idealidad. La probabilidad de romper el enlace de hidrógeno entre la molécula de agua y la celulosa es mucho mayor a una mayor concentración de moléculas de agua en la cáscara hidratada, por lo que la molécula de agua después de la rotura del enlace no forma un nuevo enlace con el nodo libre vecino, sino se traduce de la capa de hidrato. Por lo tanto, el factor preexponencial de la velocidad de reacción es pequeño a bajas concentraciones de agua y aumenta con el crecimiento de la concentración de agua en la cáscara hidratada. Cuando se logra la saturación de la cáscara hidratada (todos los nodos están ocupados), entonces k 0 no depende de la concentración de humedad. Esto se observa para el sistema de agua de MCC a una concentración superior al 12,9%.
Después de la sustitución de Eq. 1 en la ecuación. 2 y logaritmo, obtenemos:
$$ \ ln k =\ ln \ left [\ frac {-dQ / dt} {Q ^ n} \ right] =\ ln {k} _0- \ frac {E} {RT}. $$ (3)En condiciones iniciales Q t = 0 = 1, Q t =∞ = 0 y tasa de calentamiento constante ( β ), es decir, en dependencia lineal de la temperatura en el tiempo
$$ T (t) ={T} _0 + \ beta t, $$ (4)se cumplen las siguientes relaciones
$$ Q (t) =\ frac {S_T} {S_0}; - \ frac {dQ} {dt} =\ beta \ frac {f_3} {S_0}, $$ (5)donde S 0 y S T son las áreas en la parcela f 2 debajo de todo el pico y la parte del pico de T a ∞
$$ {S} _T ={\ displaystyle \ underset {T} {\ overset {\ infty} {\ int}} {f} _2dT, {S} _0 =} {\ displaystyle \ underset {0} {\ overset { \ infty} {\ int}} {f} _2dT}. $$ (6)Si todas las suposiciones que se colocan en este método son correctas y el orden de reacción n se elige correctamente, entonces la dependencia \ (\ ln \ left [\ frac {-dQ / dt} {Q ^ n} \ right] \) de la temperatura inversa (Ec. 3) es lineal en todo el rango de temperatura. Tener valores experimentales de f 3 y β , usando expresiones Ecs. 5 y 6, se puede obtener Q y dQ / dt y parámetros de cinética no isotérmica k 0 y E se calculan a partir de la Ec. 3.
Una ventaja de este método es el uso de toda la gama de datos experimentales, incluida la parte de temperatura alta del termograma, que es especialmente importante para determinar el orden n , determinación del mecanismo de reacción y equidad del modelo.
Se construyeron las dependencias de \ (\ ln \ left [\ frac {-dQ / dt} {Q ^ n} \ right] \) de una temperatura inversa para los estándares investigados (Fig. 4). Estas dependencias se aproximan mediante líneas rectas mediante el método de mínimos cuadrados. Se descubre que el coeficiente más alto de Pearson se observa en n =2.
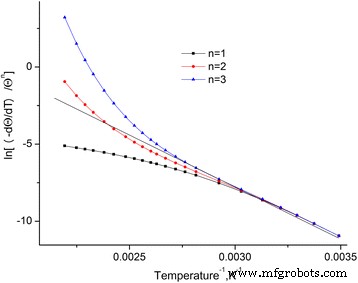
Dependencia de \ (\ ln \ left [\ frac {-dQ / dt} {Q ^ n} \ right] \) en la temperatura inversa para diferentes órdenes de reacción. Dependencia de \ (\ ln \ left [\ frac {-dQ / dt} {Q ^ n} \ right] \) en la temperatura inversa para diferentes órdenes de reacción
Energía de activación calculada ( E ) y factor preexponencial ( k 0 ) de las muestras de MCC investigadas se presentan en la Tabla 2 (ver Fig. 5). Suponiendo que la energía de activación está relacionada con el rapto de los enlaces de hidrógeno, que comprenden 25 k J / mol [10], es posible calcular su número N 1 (ver Tabla 2).
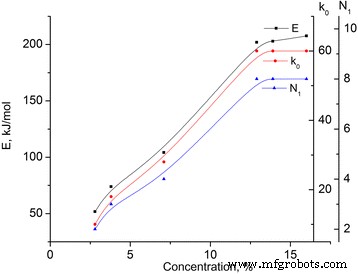
Dependencias de la energía de activación ( E ), factor preexponencial ( k 0 ) y el número de enlaces de hidrógeno N 1 para las muestras de MCC. Dependencias de la energía de activación ( E ), factor preexponencial ( k 0 ) y el número de enlaces de hidrógeno N 1 para las muestras de MCC con diferente contenido de agua
Se ve que con el aumento de la concentración de agua ligada física y químicamente, el aumento de la energía de activación ( E ), y a una concentración del 12,9%, alcanza su saturación. El valor de la energía de activación para el estado saturado corresponde a ocho enlaces de hidrógeno.
Por lo tanto, podemos suponer que a una concentración de agua del 12,9%, se forma en la muestra la capa de hidrato continua de cristales de MCC.
Análisis de difracción de rayos X
Las dependencias de la intensidad de la radiación de rayos X difractados para celulosa microcristalina con diferentes concentraciones de agua en el ángulo de difracción I (2 θ ) dentro del rango de ángulos [5 ÷ 45] ° (ver Fig. 6) con el paso de cambio de ángulo de 0.1 ° se obtuvieron.
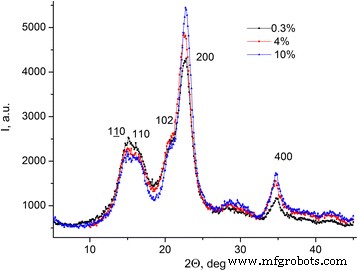
Dependencias de la intensidad de la radiación de rayos X difractada para MCC. Dependencias de la intensidad de la radiación de rayos X difractada para MCC con diferentes concentraciones de agua en el ángulo de difracción I (2 θ )
Los máximos, que corresponden a diferentes llanuras cristalográficas, se observan en el difractograma de rayos X del MCC (ver Fig. 6).
El grado de cristalinidad ( C k ) de MCC se calculó mediante la intensidad integral de la dispersión de rayos X como una relación entre los reflejos estructurales y la intensidad total del patrón de difracción excluyendo el fondo en el rango 2 θ [5 ÷ 45] ° (ver Fig. 6). Datos de C k para las muestras de MCC se presentan en la Tabla 3 [14].
Las dimensiones transversales de los cristalitos de celulosa en la dirección normal al sistema se calcularon mediante la fórmula de Debye-Sherrer [15].
$$ {B} _ {\ mathrm {hkl}} =\ frac {k \ lambda} {h \ cdot \ cos {\ theta} _ {\ mathrm {hkl}}}, $$ (7)donde k =0,94 --- factor de forma adimensional, λ --- longitud de onda de la radiación CuKα (1,54178 Å); h --- mitad de ancho del reflejo (hlk), θ hlk --- ángulo de difracción del sistema de llanuras (hlk). Se utilizó urotropina como un etalón para mayor confianza. El error instrumental se estimó utilizando el etalon y se calcularon las correcciones para la mitad del ancho del reflejo.
Datos de dimensiones B hlk para muestras de MCC con diferente contenido de agua y cristalinidad se presentan en la Tabla 3.
De los resultados obtenidos (Tabla 3 y Fig. 7) se deduce que la dimensión transversal de los cristalitos y la cristalinidad crecen con la concentración de agua. El crecimiento de las dimensiones tiene lugar en diferentes direcciones en aproximadamente 0,4 nm. El diámetro medio de la molécula de celulosa es del orden de d =0,8 nm. Por lo tanto, con el crecimiento de la concentración de agua, puede ocurrir un ordenamiento de las moléculas de celulosa en la capa límite y, como consecuencia, puede producirse un aumento de la dimensión transversal de los cristalitos de celulosa y la cristalinidad.
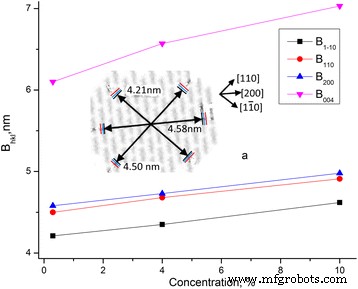
Dependencias de las dimensiones de cristalita de MCC B hlk sobre el contenido de agua. Dependencias de las dimensiones de cristalita de MCC B hlk en el contenido de agua, a --- dimensiones transversales de cristalita MCC ( negro ) y crecimiento de su dimensión con el aumento de la humedad ( azul --- MCC + 4% y rojo --- MCC + 10%)
Propiedades dieléctricas de MCC
Dependencias de temperatura de las partes reales e imaginarias de la permitividad dieléctrica compleja dentro del rango de temperatura [−180 ÷ 120] ° C en las frecuencias f =5, 10, 20 y 50 kHz para las muestras MCC + 0.3% H 2 O (véanse las Figuras 8 y 9).
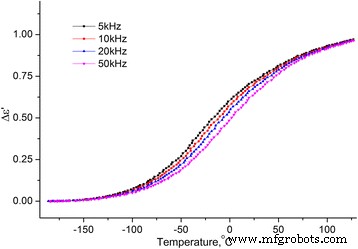
Dependencia de la temperatura del cambio de incremento de la parte real de la permitividad dieléctrica compleja. Dependencia de la temperatura del cambio de incremento de la parte real (Δ ε ′ = ε ′ ( T ) - ε ∞ , \ ({\ varepsilon} _ {\ infty} ={\ left. {\ varepsilon} ^ {\ prime} \ right |} _ {T =-180 {} ^ o \ mathrm {C}} \)) de la permitividad dieléctrica compleja MCC + 0.3% H 2 O en las frecuencias de 5, 10, 20 y 50 kHz
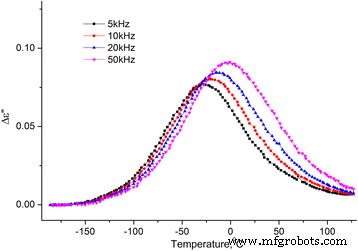
Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica de MCC + 0.3% H 2 O. Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica de MCC + 0.3% H 2 O en las frecuencias de 5, 10, 20 y 50 kHz
De los dos procesos observados en las dependencias de temperatura de ∆ ε ′ ( T ) y ε ′ ′ ( T ), la temperatura baja es una relajación ya que el máximo en ∆ ε ′ ( T ) y la inflexión en ε ′ ′ ( T ) se desplaza con el aumento de la frecuencia. Por lo general, este proceso se llama proceso β, su mecanismo molecular no se establece finalmente. Suponemos que está relacionado con la reorientación de los grupos metilol en la superficie de los cristalitos del MCC, y esta reorientación ocurre con un cambio en la conformación de los grupos metilol tg a tt , la ruptura del enlace H intramolecular y la formación del enlace H con la molécula de agua adsorbida [16].
El proceso de alta temperatura en las dependencias ∆ ε ′ ( T ) y ε ′ ′ ( T ) no cambia con la variación de frecuencia, su intensidad crece con la concentración de agua en el MCC (ver Figs. 10 y 11). Suponemos que la razón de esto es la desorción del agua con el aumento de temperatura con su posterior condensación en los poros, lo que conduce a un marcado aumento de la temperatura ε ′ Y ε ′ De la muestra. Con el aumento adicional de la temperatura, se produce la evaporación del agua y ∆ ε ′ ( T ) y ε ′ ′ ( T ) disminuir.
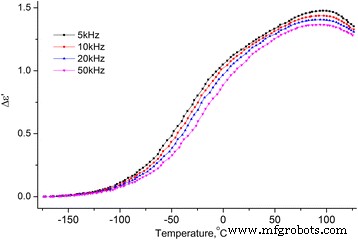
Dependencia de la temperatura del incremento de la parte real de la permitividad dieléctrica MCC + 2.8% H 2 O. Dependencia de la temperatura del incremento de la parte real (Δ ε ′ = ε ′ ( T ) - ε ∞ , donde \ ({\ varepsilon} _ {\ infty} ={\ left. {\ varepsilon} ^ {\ prime} \ right |} _ {T =-180 {} ^ oC} \)) de la permitividad dieléctrica MCC + 2.8% H 2 O en las frecuencias de 5, 10, 20 y 50 kHz
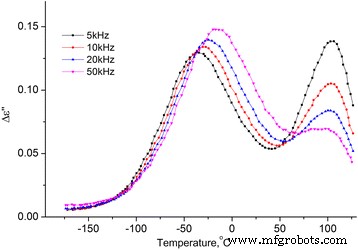
Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica de MCC + 2.8% H 2 O. Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica de MCC + 2.8% H 2 O en las frecuencias de 5, 10, 20 y 50 kHz
En la Fig.12, las dependencias del incremento de la parte real ( Δε ′ = ε ′ ( T ) - ε ∞ , donde \ ({\ varepsilon} _ {\ infty} ={\ left. {\ varepsilon} ^ {\ prime} \ right |} _ {T =-180 {} ^ oC} \)) de la permitividad dieléctrica en La temperatura en una frecuencia de 10 kHz se presenta para las muestras investigadas de MCC con diferentes contenidos de agua.
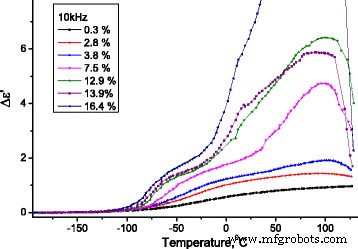
Dependencia de la temperatura del cambio de incremento de la parte real de la permitividad dieléctrica de MCC. Dependencia de la temperatura del cambio de incremento de la parte real (Δ ε ′ = ε ′ ( T ) - ε ∞ , donde \ ({\ varepsilon} _ {\ infty} ={\ left. {\ varepsilon} ^ {\ prime} \ right |} _ {T =-180 {} ^ oC} \)) de la permitividad dieléctrica de Muestras de MCC con diferente contenido de agua
Se demostró en [16] que el proceso de relajación a baja temperatura, que está conectado con la transición del grupo metilol de tg a tt conformación, puede ser descrito por el modelo con un tiempo de relajación [17]
$$ \ tau =\ frac {2 \ pi} {\ omega_0} \ frac {\ exp \ left (\ raisebox {1ex} {$ U $} \! \ left / \! \ raisebox {-1ex} {$ kT $} \ right. \ right)} {1+ \ exp \ left (\ raisebox {1ex} {$ - V $} \! \ left / \! \ raisebox {-1ex} {$ kT $} \ right. \ derecha)} $$ (8)y para el incremento de la permitividad dieléctrica es válida la siguiente fórmula:
$$ \ varDelta \ varepsilon ={\ varepsilon} ^ {\ prime} (T) - {\ varepsilon} _ {\ infty} =\ frac {N {\ mu} ^ 2} {3k {\ varepsilon} _0T} \ cdot \ frac {\ exp \ left (\ raisebox {1ex} {$ - V $} \! \ left / \! \ raisebox {-1ex} {$ kT $} \ right. \ right)} {{\ left [ 1+ \ exp \ left (\ raisebox {1ex} {$ - V $} \! \ Left / \! \ Raisebox {-1ex} {$ kT $} \ right. \ Right) \ right]} ^ 2}, $$ (9)donde ε ′ (T) –– es la permitividad dieléctrica de la muestra a temperatura T , N es la concentración de osciladores de relajación, μ 2 es el cuadrado promedio de la diferencia de los momentos dipolares de los osciladores de relajación en dos posiciones de equilibrio, y V es la diferencia de energías de los osciladores de relajación en estas posiciones de equilibrio.
Durante la aproximación de la dependencia del incremento de la parte real de la permitividad dieléctrica compleja para muestras de MCC con diferente humedad por la dependencia (Ec. 9), valores de N y V se obtuvieron (ver Tabla 4) con respecto a la diferencia de momentos dipolares de osciladores de relajación en dos posiciones de equilibrio, que se calculó con respecto a la estructura espacial del grupo metilol μ =5.57 D =18,381 ⋅ 10 - 30 C ⋅ m .
Se ve en la Tabla 4 que al aumentar el contenido de agua, la diferencia de energía V no cambia, pero la concentración de grupos metilol, que contribuye a la relajación dieléctrica, aumenta.
En la Fig.13, dependencias de la parte imaginaria de la permitividad dieléctrica de la temperatura en la frecuencia f =Se presentan 10 kHz para las muestras estudiadas de MCC con diferente contenido de agua.
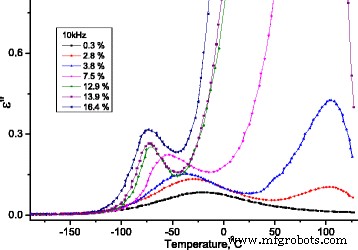
Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica para muestras de MCC con diferente contenido de agua. Dependencia de la temperatura de la parte imaginaria de la permitividad dieléctrica para muestras de MCC con diferente contenido de agua
Para el proceso de relajación con una aproximación de un tiempo de relajación ( τ = τ 0 exp (( U - TΔS ) / kT ) y bajo condición de máxima dependencia de la parte imaginaria de permitividad dieléctrica compleja ( ε ′ ′ ( T , f )) ωτ =1 , cambios de entropía ΔS / k (ver Fig.14) y energía de activación U (ver Fig. 14) con concentración de agua.
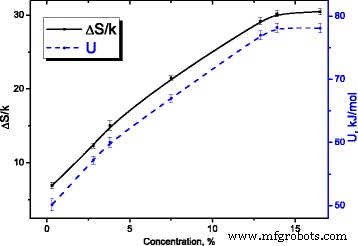
Dependencias de la entropía y la energía de activación del proceso de relajación sobre la concentración de agua en MCC. Dependencias de la entropía y la energía de activación del proceso de relajación en la concentración de agua en MCC
Suponemos que la entropía de activación del proceso de relajación está relacionada con la probabilidad de formación de enlaces de hidrógeno del grupo metilol con las moléculas de agua circundantes [18].
Su crecimiento atestigua el aumento del número medio de moléculas de agua que rodean a estos grupos en la superficie de los cristalitos de MCC.
La saturación de la dependencia ∆ S / k (ver Fig.14) al crecer la concentración de agua es una consecuencia de la formación de una capa de hidrato sólido en el sistema de cristalitos de MCC como resultado de la incorporación de grupos de superficie separados de moléculas de agua después de alcanzar su concentración umbral, que está determinada por superficie específica de agua disponible del sistema de cristalitos MCC durante su hinchamiento.
El crecimiento de la energía de activación U ( C ) del proceso de relajación (ver Fig. 14) y la saturación de su dependencia de la concentración de agua tiene la misma naturaleza que para la activación de la entropía, indica la estructuración de la superficie de los cristalitos de MCC durante la formación de su capa de hidrato sólido.
Conclusiones
Se realizaron estudios de propiedades dieléctricas, termofísicas y estructurales de muestras de MCC con diferente grado de humedad. La existencia de un proceso de relajación, que está relacionado con la reorientación de los grupos metilol de la superficie de la molécula de celulosa por el cambio de sus conformaciones de tg a tt se muestra.
Durante la retención de la muestra de MCC en el vapor de agua saturado, la capa de hidrato comienza a formarse gradualmente en la superficie de los cristalitos de celulosa. Estructura la capa límite de cristalitos de MCC. A concentración de agua, se observa una formación superior al 13% de capa de hidrato sólido en cristalitos de MCC.
La formación de la capa de hidrato da como resultado el cambio del proceso de relajación hacia el lado de las bajas temperaturas debido a su influencia en la barrera potencial y el cambio de vibraciones en las posiciones de equilibrio de los grupos metilol de la superficie de la molécula de celulosa en su transición desde la conformación tg a tt .
Nanomateriales
- ¿Qué es la aleación de cobalto y cuáles son las propiedades de la aleación de cobalto?
- El lado incómodo, impredecible y aleatorio del mantenimiento
- ¿Cuáles son las aplicaciones y propiedades del acero al manganeso?
- IoT y gestión del agua en el hogar
- Presentación de la estructura atómica y electrónica de las nanofibras de carbono de copa apilada
- Estructura y propiedades electrónicas de la nanoarcilla de caolinita dopada con metal de transición
- El efecto del plasma de no equilibrio por contacto sobre las propiedades estructurales y magnéticas de Mn Х Fe3 - X О4 Espinelas
- Efectos del espesor de la bicapa en las propiedades morfológicas, ópticas y eléctricas de los nanolaminados de Al2O3 / ZnO
- Explorando la relación de EDM y la industria aeroespacial
- Película de condensador:propiedades, construcción y aplicación
- Compresores de aire y secadores:la pareja perfecta



