Alto rendimiento mejorado de un polarizador de superficie meta mediante análisis numérico de las características de degradación
Resumen
Este estudio se centra en las investigaciones experimentales y numéricas de las características de degradación de un polarizador de metasuperficie. La metasuperficie tiene una estructura complementaria apilada que exhibe una alta tasa de extinción del orden de 10,000 en la región del infrarrojo cercano. Sin embargo, su rendimiento se ha degradado significativamente con el tiempo. Para aclarar el origen de esta degradación, se investigan numéricamente los efectos de la rugosidad superficial y la pérdida metálica. La degradación se atribuye principalmente al aumento de la pérdida. Estos cálculos numéricos también revelan que la relación de extinción se mejora ajustando los espesores de las estructuras complementarias a diferentes valores. Este estudio allana el camino para realizar un polarizador de metasuperficie que tiene una baja sensibilidad a la degradación del tiempo y tiene una alta tasa de extinción.
Antecedentes
El control de la luz a nanoescala se ha investigado ampliamente en nanoóptica y nanofotónica. Como resultado, hasta ahora se han propuesto diferentes tipos de nanoestructuras fotónicas. Por ejemplo, las nanocavidades de cristal fotónico (PhC) con factores de calidad (Q) ultra alta [1] pueden confinar la luz en una región de sublongitud de onda. Al igual que en las cavidades PhC, los factores Q altos se obtienen mediante cavidades de microdiscos [2, 3], esféricas [4] y troidales [5]. Las cavidades con factores Q altos suelen estar formadas por materiales dieléctricos transparentes. A diferencia de las cavidades dieléctricas, las cavidades metálicas tienen factores Q bajos, pero pueden reducir el tamaño completo de sus cavidades. En particular, las cavidades plasmónicas de sublongitud de onda son importantes para controlar la luz a una escala extremadamente pequeña [6]. Aunque las cavidades plasmónicas tienen factores Q bajos, pueden exprimir la luz en una región profunda de sublongitud de onda [7]. Se anticipa que esta luz extremadamente confinada será la clave para fusionar la fotónica y la electrónica [8].
Además de las nanoestructuras fotónicas mencionadas anteriormente, las metasuperficies han atraído recientemente una atención considerable para diseñar dispositivos ópticos ultradelgados y altamente funcionales. Hay varios tipos de metasuperficies que controlan la refracción [9], la reflexión [10], la fotoluminiscencia [11], la fluorescencia [12-14], las placas de onda [15] y los divisores de haz [16]. El estado de polarización es una de las propiedades fundamentales e importantes de la luz que pueden ser controladas por metasuperficies [17-22]. Estudios numéricos y experimentales han demostrado que un polarizador de metasuperficie con una estructura complementaria apilada tiene una alta tasa de extinción del orden de 10.000 en la región del infrarrojo cercano [23-26]. Las estructuras complementarias tienen resonancias en casi la misma longitud de onda debido al principio de Babinet [27, 28]. Cuando una estructura complementaria está en resonancia que exhibe una alta transmitancia para una polarización específica, la otra estructura está fuera de resonancia y exhibe una baja reflectancia para la misma polarización. Como resultado, toda la estructura presenta una alta transmitancia. Para la polarización ortogonal, el papel de los campos eléctricos y magnéticos se intercambia, lo que da como resultado una alta reflectancia. Así, la metasuperficie con estructuras complementarias exhibe una alta tasa de extinción. Sin embargo, existe una gran preocupación acerca de la estabilidad y confiabilidad de este alto rendimiento porque la metasuperficie comprende plata, que se degrada en la atmósfera. Para evitar este problema, un enfoque alternativo es utilizar oro como material plasmónico, pero esto disminuye el rendimiento del polarizador debido a una mayor pérdida metálica. Por lo tanto, para aplicaciones prácticas, se debe abordar la estabilidad y confiabilidad del polarizador de metasuperficie.
En este estudio, investigamos las características de degradación del polarizador de metasuperficie. Mostramos que la relación de extinción del polarizador exhibe degradación en el tiempo. Como origen de la degradación, nos centramos en el efecto de la morfología superficial sobre el alto rendimiento del polarizador. Para describir la morfología, presentamos dos modelos. Uno describe la rugosidad de la superficie mediante una curva periódica con un ruido blanco gaussiano, mientras que el otro describe la rugosidad mediante el uso de nanopartículas distribuidas aleatoriamente. También investigamos el efecto de la pérdida metálica en el alto rendimiento. A lo largo de estos cálculos numéricos, revelamos un factor crucial que causa la degradación y proponemos un polarizador de metasuperficie optimizado con una alta tasa de extinción.
Métodos / Experimental
La configuración experimental para la medición de la relación de extinción alta se muestra esquemáticamente en la Fig. 1. Usamos un oscilador paramétrico óptico (OPO) bombeado por un láser Nd:YAG (granate de itrio hierro) de frecuencia triplicada (Optolette 355, Opotek) como luz fuente. El ancho del pulso y la frecuencia de repetición fueron de 7 ns y 20 Hz, respectivamente. La luz inactiva del OPO se enfocó en la muestra mediante una lente y se polarizó linealmente mediante un prisma de láser Glan (GLP). La luz inactiva transmitida se midió mediante un fotodetector extendido de InGaAs (Edmund Optics). En este sistema óptico, la fluctuación de la intensidad de la luz de un solo pulso provoca una mala relación señal-ruido (S / N). Por lo tanto, para eliminar el efecto de esta fluctuación, medimos la transmitancia media de un solo pulso. Para monitorear la intensidad de la luz de un solo pulso, insertamos un par de muestreadores de haz entre la lente y el GLP. Una parte de la luz inactiva se reflejó en el segundo muestreador de haz (BS2) y luego se reflejó nuevamente en el filtro de densidad neutra reflectante (ND), que ajustó la intensidad del láser reflejado para no dañar un fotodetector. El láser sintonizado incidió en un fotodetector de InGaAs extendido (Edmund Optics) a través de un orificio, que bloqueó la luz "fantasma" innecesaria reflejada en la superficie posterior del BS2 (consulte el recuadro de la Fig. 1). El primer muestreador de haz sirve como compensador de la desviación del camino óptico.
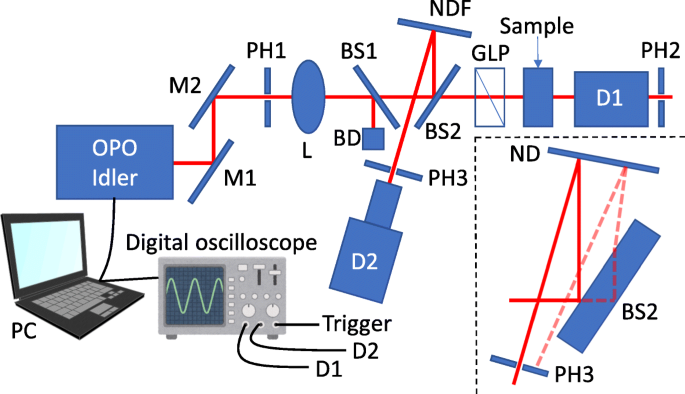
Un esquema de la configuración experimental de la medición de la relación de extinción. Espejo M, orificio de alfiler PH, lente L, muestreador de haz BS, amortiguador de haz BD, filtro de densidad neutra NDF, prisma láser GLP Glan, detector D
Usando esta configuración, evaluamos la tasa de extinción de la siguiente manera. Se calcula que la señal transmitida es D 1 =(1− R BS2 ) T GLP T Muestra yo , donde R BS2 , T GLP , T Muestra y yo son la reflectancia del BS2, la transmitancia del GLP, la transmitancia de la muestra y la intensidad de la luz frente al BS2, respectivamente. Se calcula que la intensidad de la señal del detector 2 es D 2 = R BS2 R NDF yo , donde R NDF es la reflectancia del filtro ND reflectante. Tenga en cuenta que la intensidad de la luz se reduce lo suficiente para que la señal detectada sea proporcional a la intensidad de la luz. Usando D 1 y D 2 , podemos calcular T Muestra como
$$ \ begin {array} {@ {} rcl @ {}} T _ {\ text {Sample}} =\ frac {R _ {\ mathrm {BS2}} R _ {\ text {NDF}}} {1-R_ { \ mathrm {BS2}}} \ frac {1} {T _ {\ text {GLP}}} \ frac {D_ {1}} {D_ {2}}. \ end {matriz} $$ (1)Para evaluar T Muestra , también necesitamos medir la reflectancia y transmitancia de los elementos ópticos, como el muestreador de haz. Esto es innecesario porque nuestro enfoque está en una relación de extinción, es decir, la relación de transmitancia. Al girar la muestra 90 ° y medir la transmitancia con la misma configuración, simplemente podemos obtener la relación de extinción η como
$$ \ begin {array} {@ {} rcl @ {}} \ eta =\ frac {T _ {\ text {Sample}} ^ {\ mathrm {H}}} {T _ {\ text {Sample}} ^ { \ mathrm {L}}} =\ frac {(D_ {1} / D_ {2}) ^ {\ mathrm {H}}} {(D_ {1} / D_ {2}) ^ {\ mathrm {L} }}, \ end {matriz} $$ (2)donde los superíndices H y L indican los estados de polarización que exhiben transmitancia alta y baja, respectivamente. En este artículo, medimos la relación D 1 / D 2 para los estados de polarización ortogonal y evaluó la relación de extinción η .
Para confirmar la validez de los datos medidos, realizamos cálculos numéricos basados en el análisis riguroso de ondas acopladas (RCWA) incorporado con el método de matriz de dispersión [29, 30] y un método de Fourier inverso [31]. Las permitividades de Ag y sílice se obtuvieron de [32] y [33], respectivamente. El número de vectores reticulares recíprocos utilizados en el cálculo fue 2601.
Para calcular la transmitancia de estructuras metálicas rugosas, utilizamos un software comercial de COMSOL Multiphysics, que se basa en el método de elementos finitos. En el estudio anterior [34], los efectos de la rugosidad sobre la respuesta óptica se describen mediante el aumento de la parte imaginaria de la permitividad del metal. En este trabajo, además del aumento de la pérdida metálica, también consideramos los efectos directos de los cambios estructurales seguidos de la rugosidad sobre la transmitancia. Tratamos estos dos efectos por separado. Al considerar solo los efectos de los cambios estructurales, aplicamos la permitividad aparente a las estructuras metálicas con rugosidad. Por otro lado, al considerar solo los efectos del aumento de pérdida, aplicamos la permitividad modificada a estructuras metálicas sin rugosidad. Establecimos la tolerancia relativa de los cálculos numéricos en menos del 1%.
Resultados y discusión
La Figura 2a muestra el esquema del polarizador de metasuperficie de tres capas. La primera capa tiene una estructura complementaria a la tercera capa (ver Fig. 2b), y ambas capas comprenden plata (Ag). La segunda capa y el sustrato comprenden sílice (SiO 2 ). Como se muestra en la Fig. 1c, la metasuperficie tiene una matriz de un par de orificios rectangulares (150 nm × 540 nm) y tiene un período de 900 nm en el x y y direcciones. Los espesores de las capas metálicas y dieléctricas son de 45 y 200 nm, respectivamente (ver Fig. 2d). La muestra se preparó mediante litografía de nanoimpresión junto con técnicas posteriores de grabado en seco [35]. Los detalles de la preparación de la muestra se describen en [26]. La Figura 3 muestra las imágenes de microscopio electrónico de barrido (SEM) de la muestra preparada.
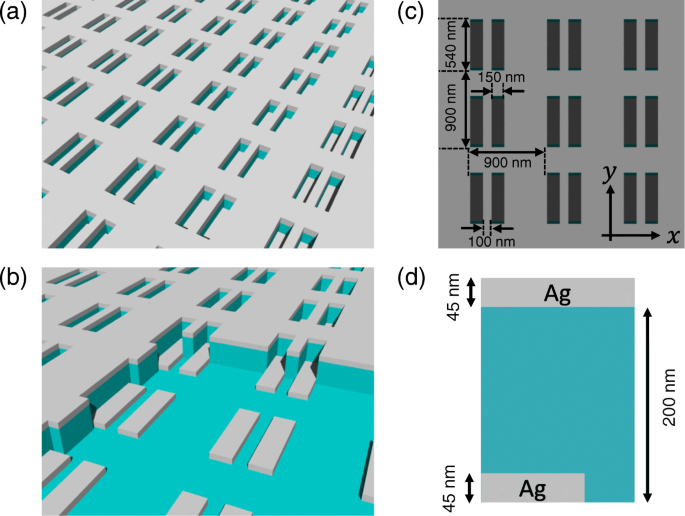
Un esquema del polarizador de metasuperficie ( a ) que consta de tres capas ( b ). La metasuperficie tiene una matriz de pares de orificios rectangulares con un período de 900 nm en el x y y indicaciones ( c ). Los espesores de las capas metálicas y dieléctricas son de 45 y 200 nm, respectivamente ( d )

La imagen SEM de a el polarizador de metasuperficie y b su imagen ampliada
Usamos un espectrofotómetro (V-7200, JASCO, Japón) para medir la transmitancia de la muestra para x y y polarizaciones. La figura 4 muestra los resultados medidos. Las líneas azul y verde indican la transmitancia de la x y y polarizaciones, respectivamente. La línea azul que corresponde a la alta transmitancia se mide con una alta relación S / N. Sin embargo, la línea verde correspondiente a la baja transmitancia sufre de una baja relación S / N, lo que indica que el polarizador tiene una alta relación de extinción. En particular, la línea verde tiene señales negativas en longitudes de onda superiores a 1350 nm porque la intensidad de la luz transmitida está por debajo del nivel de ruido del espectrofotómetro. Por lo tanto, usamos el sistema óptico descrito en la sección anterior para medir la alta tasa de extinción.
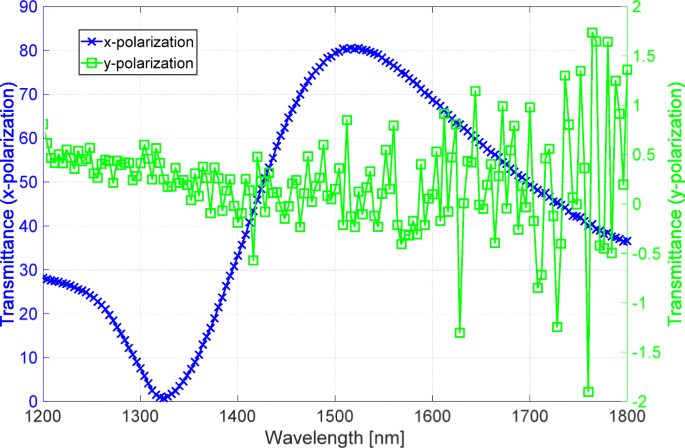
Espectros de transmitancia medidos por el espectrofotómetro. Las líneas azul y verde son los espectros de x y y polarizaciones, respectivamente
La Figura 5a muestra los espectros de transmitancia medidos para x y y polarizaciones. La línea azul que corresponde a la alta transmitancia tiene un perfil espectral similar a la transmitancia medida por el espectrofotómetro. La línea verde correspondiente a la baja transmitancia tiene una clara caída alrededor de la longitud de onda de 1625 nm, que no fue medida por el espectrofotómetro. Al dividir la transmitancia de x polarización por eso para el y polarización, evaluamos el espectro de la relación de extinción que se muestra en la Fig. 5b. El espectro de la relación de extinción tiene un valor máximo superior a 20.000 alrededor de la longitud de onda de 1640 nm.
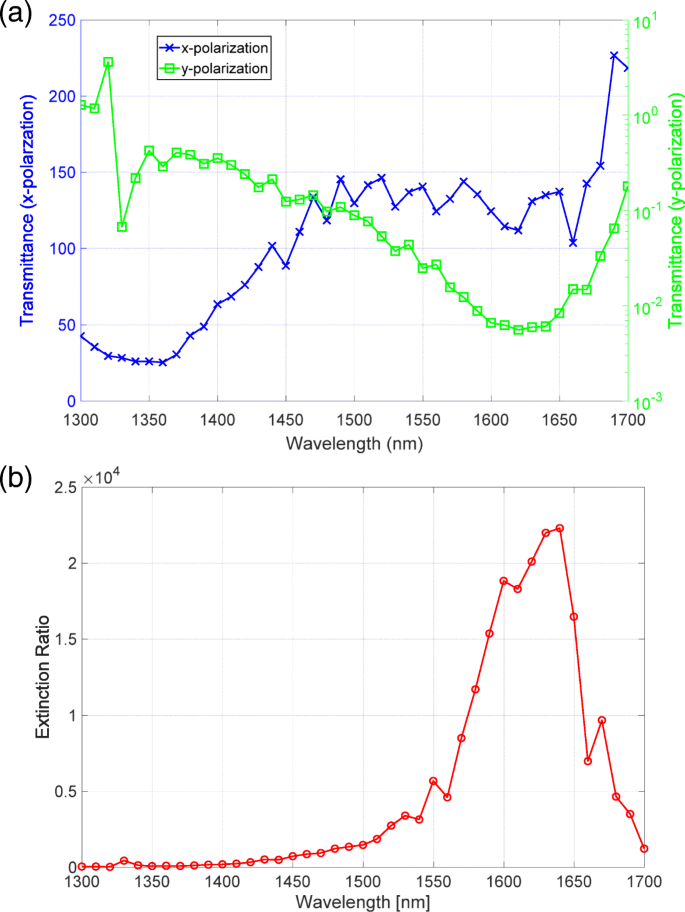
un Espectros de transmitancia para x (azul) y y polarizaciones (verdes) medidas por la configuración que se muestra en la Fig. 1. b El espectro de la relación de extinción del polarizador de metasuperficie
Para considerar la validez de los datos medidos, comparamos los espectros medidos con los resultados del cálculo numérico. Como se muestra en la Fig. 6a, el espectro de alta transmitancia fue consistente con los espectros medidos por el espectrofotómetro. El espectro de baja transmitancia, que se muestra en una escala logarítmica, tiene una clara caída alrededor de la longitud de onda de 1640 nm. Esta característica concuerda bien con la del espectro observado. El espectro de la relación de extinción que se muestra en la Fig. 6b tiene un pico de 15.000, que está cerca del valor observado. Por lo tanto, los espectros de transmitancia y relación de extinción medidos fueron consistentes con los resultados del cálculo numérico, lo que indica que habíamos observado con éxito la alta relación de extinción superior a 20.000.
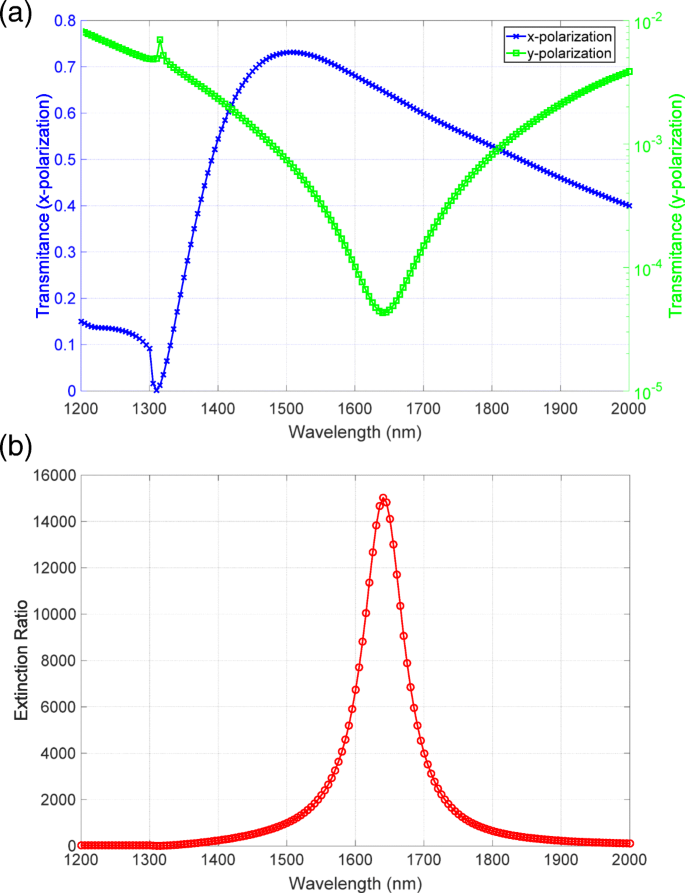
Resultados de cálculos numéricos de a transmitancia y b espectros de relación de extinción. Las líneas azul y verde en a corresponden a la x y y polarizaciones, respectivamente
Después de la demostración experimental de la metasuperficie con el alto índice de extinción, nos centramos en la estabilidad frente a la degradación en el tiempo porque la metasuperficie comprende Ag, que está sujeta a degradación en la atmósfera. La Figura 7 muestra la degradación temporal de la tasa de extinción. Las líneas roja, verde y azul son los espectros de la relación de extinción observados después de 6, 7 y 9 días después de la deposición del metal, respectivamente. La línea roja tiene un valor máximo superior a 20.000. Después de un solo día de la medición de la línea roja, la tasa de extinción se degradó, pero aún tenía un valor máximo superior a 10.000. Sin embargo, dos días después de la medición de la línea verde, el índice de extinción se degradó significativamente y tuvo un valor máximo de 500. La línea azul tiene un ancho de línea ampliado, lo que indica que un aumento en la pérdida estaría involucrado en esta degradación. Por lo tanto, la relación de extinción exhibió una degradación drástica y el rendimiento degradó un orden de magnitud. También encontramos los picos desplazados al azul de los espectros de la relación de extinción después de la degradación. Se describe un estudio del factor crucial que implica la degradación del rendimiento.
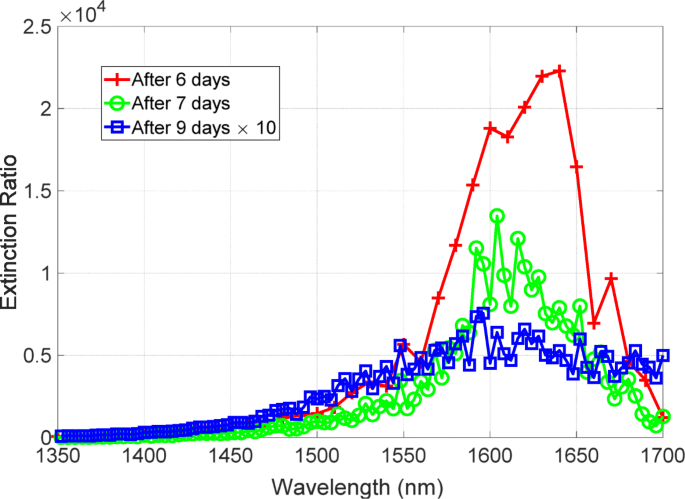
Tiempo de degradación de la tasa de extinción. Las líneas roja, verde y azul son los espectros de la relación de extinción durante 6, 7 y 9 días después de la deposición del metal
La degradación procedió rápidamente y los anchos de línea de los espectros de extinción se ampliaron, lo que indica que algunos cambios estructurales estarían involucrados en este proceso de degradación. Por lo tanto, investigamos la forma en que la morfología de la superficie de la nanoestructura metálica afecta el rendimiento del polarizador. Para describir la morfología, presentamos dos modelos. Uno describe la superficie mediante una curva periódica con ruido blanco gaussiano y el otro mediante nanopartículas distribuidas aleatoriamente.
Primero, investigamos el modelo usando la curva periódica. La figura 8a muestra la superficie modelada. Introdujimos la rugosidad solo en la capa metálica inferior para ahorrar tiempo de CPU y recursos de memoria. Debido a la superficie rugosa, el espesor efectivo de la capa metálica varía. Por lo tanto, variamos el grosor de la capa inferior indicada por la flecha verde en la Fig. 8b. La Figura 9a, b muestra los espectros de transmitancia y relación de extinción de esta estructura, respectivamente. Incluso en presencia de la rugosidad, el polarizador de metasuperficie tiene altas relaciones de extinción del orden de 10.000, lo que indica que la rugosidad no degrada significativamente el rendimiento. Los cálculos numéricos también han mostrado los espectros desplazados al rojo de la relación de extinción con la disminución del espesor. Este desplazamiento al rojo se aclara mediante las características espectrales de transmitancia mostradas en la Fig. 9a. La alta transmitancia tiene una sensibilidad muy baja en relación con la variación en el espesor del metal, mientras que la baja transmitancia tiene la posición de inmersión desplazada al rojo con la disminución del espesor. La posición máxima de la relación de extinción depende de la caída de la transmitancia baja, lo que da como resultado el desplazamiento al rojo. El desplazamiento al rojo que apareció en el cálculo no concuerda con la característica observada experimentalmente del desplazamiento al azul.
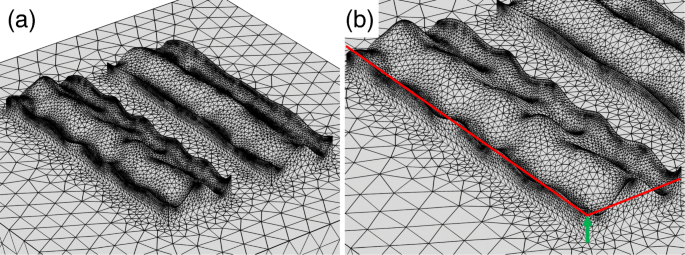
un Superficie rugosa modelada usando una curva periódica con ruido blanco gaussiano. b El grosor de la base indicado por la flecha verde se varía en el cálculo
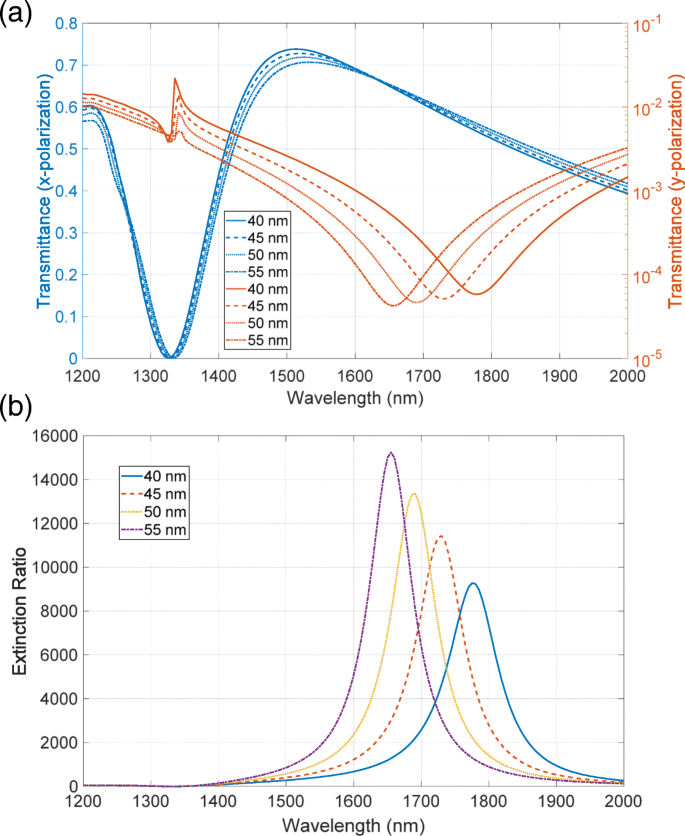
un Transmitancia y b Espectros de relación de extinción del primer modelo que se muestra en la Fig. 8. El espesor de la base de la capa metálica inferior se varía de 40 a 55 nm con un paso de 5 nm
En segundo lugar, investigamos el modelo mediante nanopartículas. La figura 10a muestra la superficie modelada, donde las nanopartículas con radios de 15, 20 y 25 nm se distribuyen aleatoriamente en la superficie de la estructura metálica inferior, como se muestra en la figura 10b. Colocamos las nanopartículas en forma de hemisferio en la superficie de acuerdo con números aleatorios distribuidos uniformemente. Bajo la distribución aleatoria, algunas de las partículas tienen una ligera superposición espacial y el tamaño de la malla entre las partículas consume mucha memoria. En este caso, para guardar la memoria, cambiamos manualmente una de las partículas y bajamos el tamaño de la malla. Establecimos el grosor de la estructura del fondo en 40 nm. La Figura 11a, b muestra los espectros de transmitancia y relación de extinción de esta estructura, respectivamente. Al igual que en el primer modelo, el espectro de la relación de extinción tiene un valor máximo del orden de 10.000 y no se degrada significativamente. El pico desplazado al rojo también ha aparecido en presencia de las nanopartículas. Estas características también son las mismas que las observadas en el primer modelo, pero no concuerdan con el resultado experimental de las características de degradación y el desplazamiento azul.
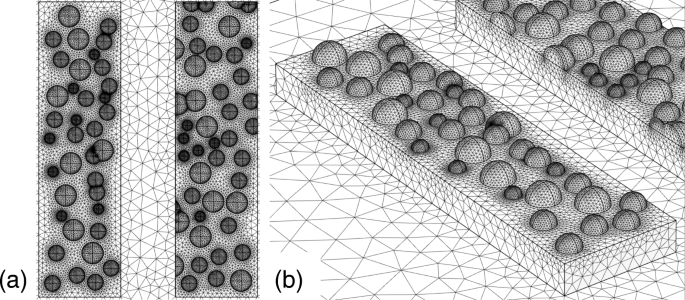
un La vista superior y b vista de pájaro de la superficie rugosa modelada con nanopartículas distribuidas aleatoriamente
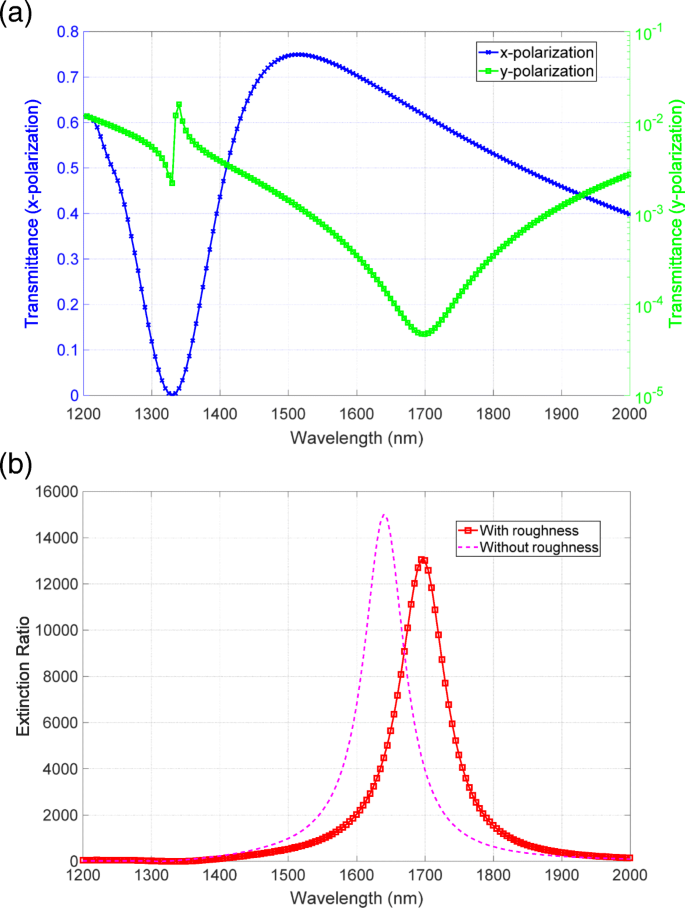
un Transmitancia y b espectros de extinción del segundo modelo que se muestra en la Fig. 10
En esta etapa, hemos demostrado numéricamente que la variación en la morfología de la superficie no degrada significativamente el rendimiento del polarizador de metasuperficie. Esta robustez de la morfología se atribuye al principio de Babinet. El principio de Babinet no se refiere a la morfología de la superficie sino a las pantallas de las estructuras complementarias. El polarizador de alto rendimiento basado en este principio no se ve muy afectado por la morfología porque las pantallas son invariables incluso en presencia de la rugosidad de la superficie, lo que da como resultado la robustez de la morfología. Por tanto, como origen de la degradación, debemos considerar otro efecto de la morfología superficial. Aquí, nos centramos en la pérdida metálica relacionada con la morfología. Con el aumento de la rugosidad de la superficie, la parte imaginaria de Ag aumenta debido a la dispersión de la superficie y los efectos de la frontera del grano [36, 37]. Este aumento en la pérdida se explica por la constante de amortiguamiento del modelo de Drude descrito como γ = ρ n e 2 / m e , donde ρ , n , e y m e son respectivamente la resistividad eléctrica, la densidad electrónica, la carga electrónica y la masa electrónica efectiva. La resistividad consta de dos términos. Una es la resistividad aparente y la otra es la superficial. La resistividad superficial ρ s es inversamente proporcional a la longitud correlacional lateral ξ , a saber, ρ s ∝ ξ −1 [38]. Con el aumento de la rugosidad, la longitud de correlación lateral ξ disminuye, lo que resulta en una mayor resistividad superficial y pérdida metálica. Este mecanismo físico no se incluyó en el cálculo porque se utilizó una condición de contorno periódica y se asumió una estructura periódica aproximada. Consideramos los efectos de este aumento en la pérdida metálica sobre la razón de extinción y modificamos la permitividad de Ag de la siguiente manera:
$$ \ begin {array} {@ {} rcl @ {}} \ tilde {\ epsilon} _ {\ text {Ag}} =\ text {Re} \ left (\ epsilon _ {\ text {Ag}} \ right ) + C \ times \ text {Im} \ left (\ epsilon _ {\ text {Ag}} \ right) \ mathrm {i}, \ end {array} $$ (3)donde ε Ag es la permitividad de Ag obtenida de [32], C es una constante que representa el aumento de la pérdida metálica e i denota una unidad imaginaria. Tenga en cuenta que la parte real de la permitividad debe modificarse siguiendo el aumento de la parte imaginaria porque las partes real e imaginaria están conectadas por la relación Kramers-Kronig. En este estudio, modificamos solo la parte imaginaria para tener una discusión cualitativa. Usando esta permitividad modificada, calculamos el espectro de la relación de extinción. Este resultado se muestra en la Fig.12, en la que la constante C varía de 1 a 5. La relación de extinción disminuye drásticamente con un aumento de la pérdida metálica. Además, la posición de pico del espectro exhibió la característica desplazada al azul con el aumento de la pérdida. Estas características de la degradación drástica y el cambio al azul concuerdan bien con las características observadas experimentalmente. El origen de este cambio al azul se aclara de la siguiente manera. El valor de inmersión de la baja transmitancia se vuelve cada vez más superficial con el aumento de la pérdida metálica. Como resultado, aumenta la contribución del valor pico de la alta transmitancia a la relación de extinción. La posición del pico tiene una fuerte insensibilidad a la pérdida metálica y se encuentra en la longitud de onda más corta que la posición de inmersión, lo que da como resultado el desplazamiento hacia el azul del espectro de extinción. Así, hemos encontrado que el aumento de la parte imaginaria es un factor crucial responsable de la degradación.
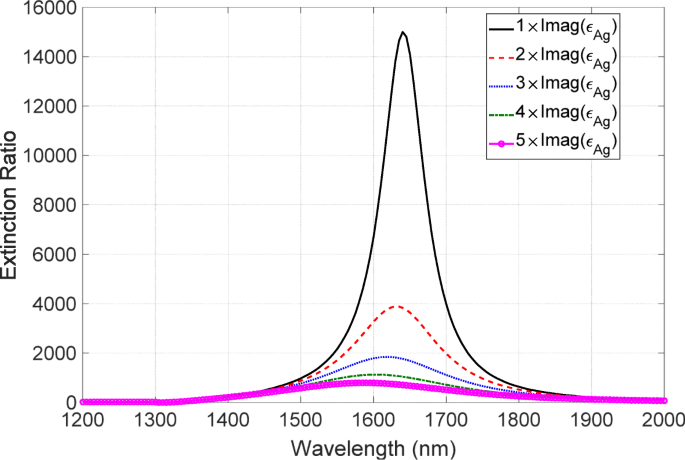
Dependencia de pérdidas metálicas de los espectros de extinción. Las líneas negra, roja, azul, verde y magenta corresponden a los casos de C =1, 2, 3, 4 y 5, respectivamente
Proponemos que la relación de extinción se mejore variando los espesores de las capas metálicas complementarias. La posición máxima de la transmitancia alta se encuentra en una longitud de onda más corta que la posición de inmersión de la transmitancia baja. Para mejorar la relación de extinción, estas posiciones de pico y caída deben estar próximas entre sí. Según el principio de Babinet, el pico y la caída deben tener la misma longitud de onda. Sin embargo, el principio asume que las estructuras complementarias comprenden un conductor eléctrico perfecto con un espesor infinitamente delgado, lo que es difícil de validar en la región óptica incluso bajo aproximación. Como resultado, las estructuras complementarias tienen diferentes longitudes de onda de resonancia. Para ajustar las longitudes de onda, consideramos las características de los modos propios responsables de las resonancias. La Figura 13a, b muestra los patrones de distribución del campo eléctrico y magnético en las posiciones de pico y caída de la transmitancia mostrada en la Figura 6, respectivamente. Estas distribuciones de campo se muestran en la z - x avión en y =0 bajo la intensidad de luz incidente de 1 W. El modo propio de alta transmitancia tiene una característica de dipolo eléctrico en la estructura metálica superior, mientras que el de baja transmitancia tiene una característica de bucle magnético en la estructura inferior. La longitud de onda de resonancia para la alta transmitancia está determinada por el ancho del orificio de aire en el z - x avión. Este es un parámetro fijo e imposible de ajustar. Por otro lado, la longitud de onda de resonancia para la baja transmitancia está determinada por la sección transversal de la estructura inferior en el z - x avión. Esto se puede ajustar variando el grosor del metal. Estos ajustes son consistentes con la dependencia del espesor de la transmitancia de que la posición de pico de la transmitancia alta tiene una sensibilidad baja al espesor de la capa metálica inferior mientras que la posición de inmersión de la transmitancia baja tiene una sensibilidad alta. Con base en este análisis, ajustamos la longitud de onda de la siguiente manera. Con el aumento del espesor, la sección transversal aumenta y la longitud de onda de resonancia de la baja transmitancia cambia a longitudes de onda más cortas. Como resultado, las posiciones de pico y caída se acercan y se mejora la relación de extinción. Para confirmar esto, calculamos la dependencia de los espectros de transmitancia y relación de extinción del espesor. En este cálculo, fijamos el grosor de la capa metálica superior en 45 nm. La Figura 14a muestra los espectros de transmitancia para x y y polarizaciones. Con el aumento del espesor, la posición de inmersión de la transmitancia baja cambia a longitudes de onda más cortas y la inmersión se vuelve más profunda. Por otro lado, la posición del pico de alta transmitancia no se ve fuertemente afectada por la variación del grosor, aunque el valor pico disminuye en ∼ 5%. La Figura 14b muestra los espectros de la relación de extinción. Cuando el espesor es de 35 o 40 nm, la caída de la transmitancia baja se vuelve menos profunda que la de 45 nm, lo que da como resultado una relación de extinción más baja. Cuando el grosor es de 50 o 55 nm, casi no hay realce. Esto se debe a que la mejora mediante el ajuste de las posiciones de pico y caída se cancela mediante la disminución del valor de pico de la alta transmitancia. Cuando el espesor es de 60 o 65 nm, hay una clara mejora en la relación de extinción. Esto se debe a la combinación del valor de caída más profunda y la mejora por el ajuste de posición. Como hemos mostrado numéricamente, se puede realizar una mejora adicional de la relación de extinción ajustando los espesores de las estructuras metálicas complementarias. Tales espesores variables se podrían realizar repitiendo la deposición de metal. Primero, deposición de metal con un espesor de a se realiza sobre un sustrato estampado. Luego, limpiando con un paño limpio, solo se retira la capa metálica superior de la superficie del sustrato con un espesor de metal de a . Posteriormente, la deposición de metal con un espesor de b se realiza sobre la muestra. Como resultado, los espesores de las capas superior e inferior se vuelven b y a + b , respectivamente.
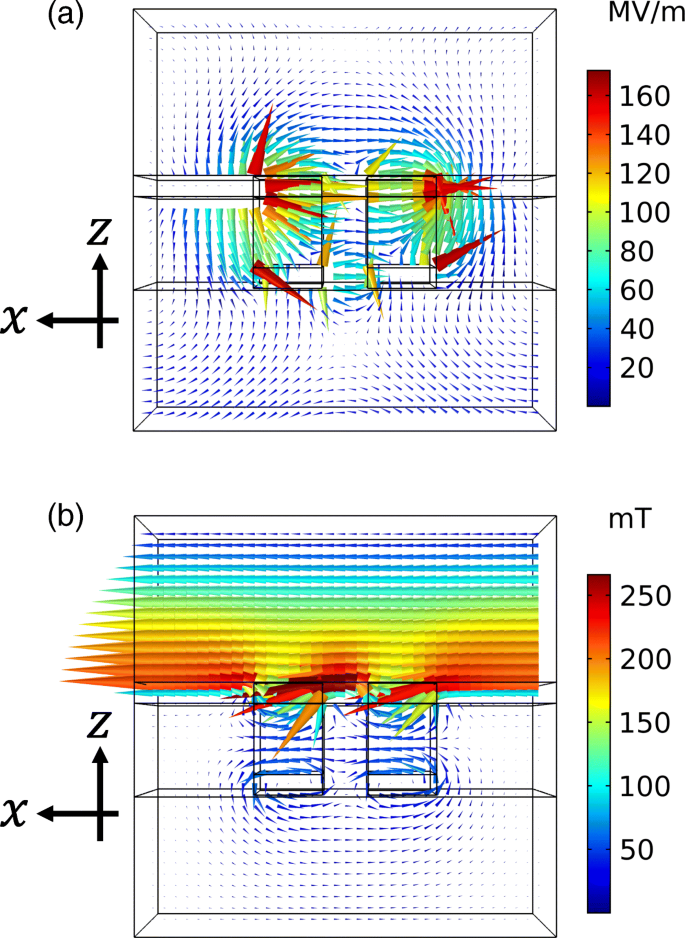
un Patrón de distribución del campo eléctrico en el pico de alta transmitancia que se muestra en la Fig. 6. b Patrón de distribución del campo magnético en la caída de la baja transmitancia que se muestra en la Fig. 6. El pseudo color indica la intensidad del campo vectorial
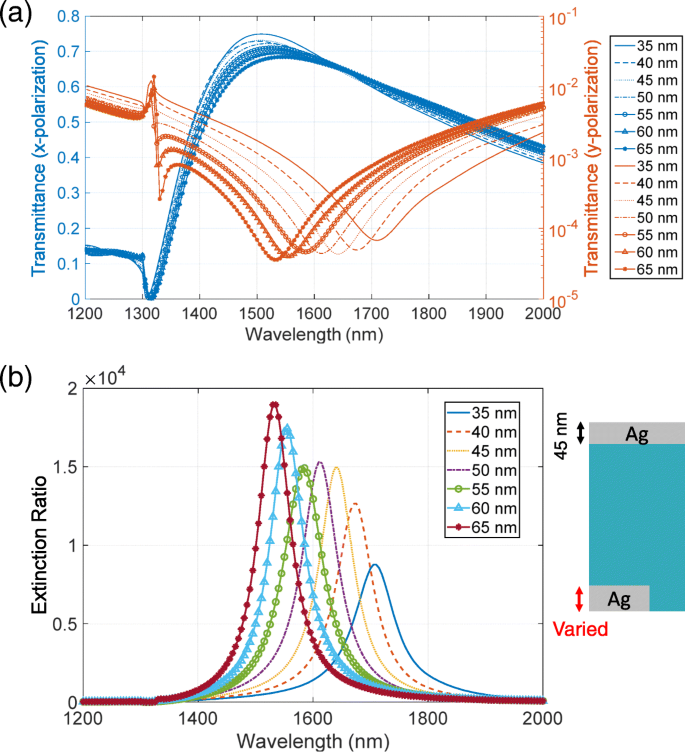
un Transmitancia y b espectros de relación de extinción cuando las capas metálicas complementarias tienen diferentes espesores. El grosor de la capa metálica superior se fija en 45 nm, mientras que el de la capa inferior se varía de 35 a 65 nm con un paso de 5 nm (ver el recuadro en b )
Conclusiones
Hemos investigado las características de degradación del polarizador de metasuperficie de alto rendimiento. La metasuperficie preparada exhibió una alta tasa de extinción del orden de 10,000. Notamos que el alto rendimiento se ha degradado gradualmente. Para aclarar el origen de esta degradación, hemos investigado los efectos de la morfología de la superficie en la tasa de extinción. Se presentaron dos modelos para describir la morfología de la superficie. Uno modela una superficie rugosa mediante una combinación de una curva periódica y un ruido blanco gaussiano, mientras que el otro modela la superficie mediante nanopartículas distribuidas aleatoriamente. Ambos modelos indicaron que el alto rendimiento no se degradaba por la rugosidad de la superficie. Esto se debe a que la alta tasa de extinción se rige por el principio de Babinet, lo que da como resultado la robustez de la morfología de la superficie. We have also investigated the relation between the extinction ratio and the increase in metallic loss because of the surface roughness, which showed drastic degradation of the extinction ratio. The spectral feature of the blue-shift was also reproduced by the numerical calculation, indicating that the degradation is due to the increase in the metallic loss. From this result, we find that the metal deposition should be conducted to reduce the scattering and grain boundary losses that are related to the roughness. Throughout the numerical calculation, we have found that the low transmittance has a high sensitivity to the surface morphology, while the high transmittance does not have the high sensitivity. By utilizing these findings, we proposed that the extinction ratio can be enhanced by varying the thicknesses of the metallic layers. This study paves a way for the development of a metasurface with a high performance and stability toward time degradation.
Abreviaturas
- BS:
-
Beam sampler
- GLP:
-
Glan-laser prism
- NDF:
-
Neural density filter
- OPO:
-
Optical parametric oscillator
- PhC:
-
Photonic crystal
- SEM:
-
Microscopio electrónico de barrido
- YAG:
-
Yttrium iron garnet
Nanomateriales
- Los conceptos básicos del análisis de vibraciones
- El rendimiento de la fibra de vidrio
- Plásticos de alto rendimiento en la industria de semiconductores
- Vespel®:el material aeroespacial
- Metasuperficie de gradiente de fase totalmente dieléctrica que realiza una transmisión anómala de alta eficiencia en la región del infrarrojo cercano
- Alto rendimiento fotocatalítico de dos tipos de fotocatalizadores compuestos de TiO2 modificado con grafeno
- La detección fotoelectroquímica mejorada de ácido úrico en electrodo de carbono vítreo modificado con nanopartículas de Au
- Un nuevo fotocatalizador de heterounión Bi4Ti3O12 / Ag3PO4 con rendimiento fotocatalítico mejorado
- Protocalabazas a través de los años
- Torneado de alto rendimiento
- La importancia del análisis de causa raíz



