Metasuperficie de gradiente de fase totalmente dieléctrica que realiza una transmisión anómala de alta eficiencia en la región del infrarrojo cercano

Diseño y métodos

Para una metasuperficie de gradiente de fase, la morfología geométrica y los parámetros influyen en gran medida en el rendimiento del dispositivo. Como se muestra en la Fig. 1, primero investigamos una estructura de matriz simple compuesta de nanobarras hexagonales regulares basadas en un sustrato de sílice. La eficiencia de transmisión y las distribuciones de fase de la estructura de matriz simple se analizan utilizando el método FDTD. En la simulación, el x - y y -direcciones se establecen como condiciones de contorno periódicas, y la z -La dirección se establece como capas perfectamente combinadas. Establecemos una onda eléctrica transversal (TE) normal para que incida en el fondo. La dirección del campo eléctrico de la luz incidente es a lo largo de y -dirección, y el rango de longitud de onda es 1400-1600 nm. En el análisis numérico, los índices de refracción del silicio y la sílice se toman de los datos propuestos por Palik [35]. Experimentalmente, para fabricar un sustrato de sílice medio ilimitado, se debe realizar un proceso de grabado. También necesitamos depositar una película de silicio de 1200 nm sobre el sustrato de sílice mediante el método de deposición química de vapor a baja presión (LPCVD). La película de silicio se reviste por rotación con fotorresistente ZEP520A, y luego se deposita una capa delgada de Cr como la capa protectora. Las nanovarillas dieléctricas hexagonales se pueden obtener mediante litografía por haz de electrones (EBL). Finalmente, el removedor 1165 y el plasma \ (O_2 \) se utilizan para eliminar el fotorresistente, produciendo la metasuperficie de gradiente de fase totalmente dieléctrica diseñada [4, 6]. Sin embargo, la sección transversal de nanobarras hexagonales regulares puede parecerse a un círculo debido a los efectos de proximidad en la fabricación experimental práctica. Para solucionar este problema, podemos ajustar la corrección del efecto de proximidad (PEC) y la dosis de EBL según la morfología de la muestra. Al ajustar el esquema, creemos que eventualmente podemos obtener metasuperficies hexagonales regulares fabricadas con precisión.

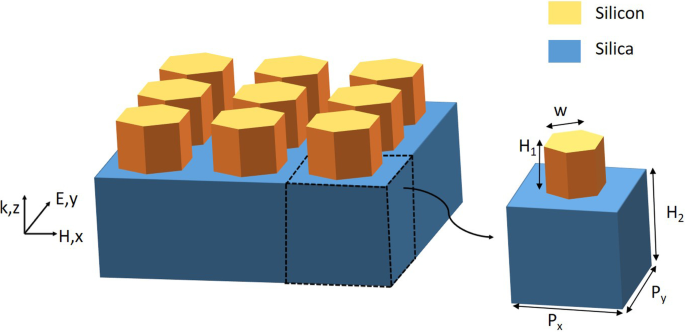
Esquema de una estructura de matriz simple compuesta por nanobarras de silicio hexagonales regulares sobre un sustrato de sílice

A diferencia del límite ideal, cuando la luz se propaga a través de la metasuperficie, las propiedades ópticas, como el estado de polarización, la fase y el frente de onda, cambian sustancialmente. No podemos explicar estos fenómenos con la ley de Snell clásica en óptica geométrica cuando las ondas electromagnéticas se propagan a través de estas interfaces, dando lugar a una ley de Snell generalizada universal [8,9,10,11,12]. Según la ley de Snell generalizada, se produce una reflexión o refracción anómala en la interfaz de dos medios debido a la distribución de fase horizontal. Podemos expresar los dos tipos de refracción como

donde \ (\ theta _r \) representa el ángulo de refracción o ángulo de refracción anómalo y \ (\ theta _i \) representa el ángulo de incidencia. El índice de refracción \ (n_r \) generalmente se refiere al índice de refracción del aire, que tiene una magnitud de 1. En contraste, \ (n_i \) se refiere al índice de refracción del material de metasuperficie, \ (\ lambda _0 \) es la longitud de onda operativa en el espacio libre, y d \ (\ phi \) / \ ({\ text {d}} x \) es el gradiente de fase. La metasuperficie de gradiente de fase necesita lograr un cambio de fase \ (2 \ pi \) casi lineal completo durante un período largo para controlar la transmisión anómala; por lo tanto, el gradiente de fase es

donde \ (P_x \) es el período de la metasuperficie propuesta a lo largo de la x -eje. En este trabajo, consideramos solo la luz normal que incide en la interfaz; por lo tanto, \ (\ theta _i \) es 0, y la ecuación se puede simplificar aún más como

Las metasuperficies de gradiente de fase exhiben no solo una transmisión anómala de bajo orden sino también una transmisión anómala de alto orden. Para determinar el ángulo de refracción anómalo de alto orden, introducimos la ecuación de rejilla para modificar la ley de Snell generalizada [36,37,38]. La ley de Snell generalizada modificada es

donde m representa el orden de difracción tradicional. Los cambios de ondas electromagnéticas desde la posición del orden cero original a la posición del primer orden pueden usarse para determinar el ángulo de refracción anómalo. Además, el período y la longitud de onda operativa determinan el número total de órdenes de difracción. La relación de \ (\ lambda _0 \) a \ (P_x \) influye en el valor deseado de m. Cuando \ (\ lambda _0 \) / \ (P_x \) es mayor que 0.5, m puede tomar solo un valor de 0, en cuyo caso solo se pueden obtener tres órdenes de difracción:0, −1 y 1. Sin embargo, cuando \ (\ lambda _0 \) / \ (P_x \) es menor que 0.5, m puede tomar un valor de 0 o 1, en cuyo caso se pueden obtener cinco órdenes de difracción:\ (- 2, -1, 0, 1 \) y 2. En la siguiente discusión, esta teoría está probada por nuestros resultados calculados .

Para explicar las características de la estructura propuesta, calculamos principalmente la eficiencia y el ángulo de refracción para la transmisión anómala. La eficiencia de transmisión total y la eficiencia de transmisión anómala se definen como

donde \ (I _ {\ mathrm {in}} \) es la intensidad de entrada, \ (I _ {\ mathrm {out}} \) es la intensidad de transmisión total y \ (I_r \) es la intensidad transmitida a lo largo de la refracción anómala ángulo.

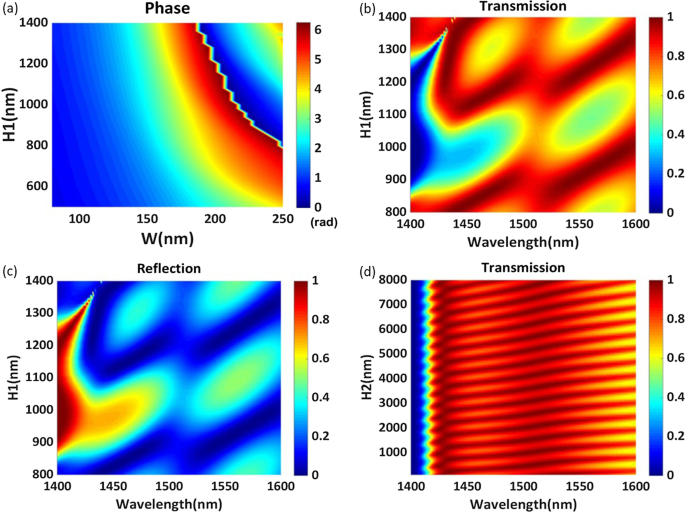
un Fase de nanovarillas hexagonales regulares periódicas para diferentes parámetros estructurales \ (H_1 \) y w a una longitud de onda de 1529 nm. b La eficiencia de transmisión y c la eficiencia de reflexión de la estructura periódica para diferentes espesores \ (H_1 \) en el rango de longitud de onda de 1400–1600 nm. d Eficiencia de transmisión de la estructura periódica para diferentes espesores \ (H_2 \) en el rango de longitud de onda de 1400 a 1600 nm

Para la estructura propuesta, esperamos lograr un cambio de fase completo de 2 \ (\ pi \) ajustando la altura \ (H_1 \) y la longitud del lado del hexágono regular w . Establecemos el período P a 500 nm, y establezca el espesor del sustrato \ (H_2 \) en 7050 nm. Dado que el espesor del sustrato \ (H_2 \) es mayor que \ (4 \ lambda \), podemos considerar que el sustrato es un sustrato medio ilimitado. Las variaciones de fase con el cambio en \ (H_1 \) y w a una longitud de onda de 1529 nm se muestran en la Fig. 2a. Está claro que la fase de la luz transmitida varía con la longitud del lado del hexágono regular w , pero solo cuando la altura \ (H_1 \) es mayor que 800 nm puede esta estructura realizar un cambio de fase completo de 2 \ (\ pi \). La alta eficiencia de transmisión es otro factor que debe tenerse en cuenta al diseñar metasuperficies de gradiente de fase. La Figura 2b, c muestra los cambios en la eficiencia de transmisión y la eficiencia de reflexión con la longitud de onda para diferentes alturas \ (H_1 \) de las nanovarillas periódicas, que se muestran en la Fig. 1. El parámetro estructural w está configurado en 160 nm. Como se muestra en la Fig. 2b, la longitud de onda de la eficiencia de transmisión máxima se desplaza al rojo con el aumento de la altura de la nanovarilla. Evidentemente, la altura de las nanovarillas tiene un efecto notable sobre la eficiencia de transmisión y la eficiencia de reflexión. Aquí, para obtener una alta eficiencia de transmisión, la altura \ (H_1 \) se establece en 1200 nm. Con este valor, la eficiencia de transmisión más alta de la metasuperficie homogénea simple es tan alta como 98.70% a una longitud de onda de 1540 nm. La Figura 2d describe el cambio en la eficiencia de transmisión con la longitud de onda para diferentes alturas \ (H_2 \). La eficiencia de transmisión cambia periódicamente al aumentar el espesor del sustrato \ (H_2 \).

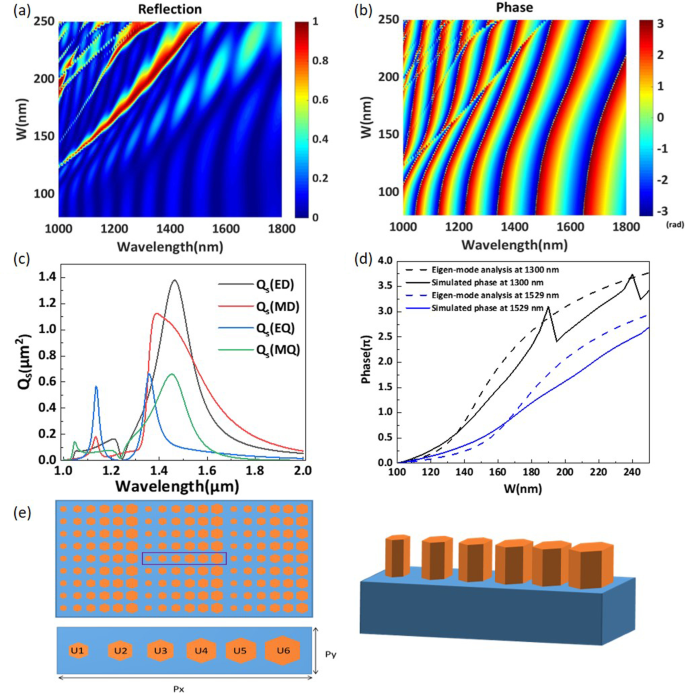
un La eficiencia de reflexión y b la fase de las nanovarillas hexagonales regulares periódicas para diferentes valores de w en el rango de longitud de onda de 1000–1800 nm. c Sección transversal de dispersión \ (Q_s \) frente a la longitud de onda de una nanovarilla de silicio hexagonal regular aislada. Se muestra la contribución de cada término a la expansión de Mie. d Perfiles de fase obtenidos mediante análisis de modo propio y simulaciones numéricas para longitudes de lados variables w . e Esquema de la metasuperficie de gradiente de fase diseñada

La Figura 3a, b ilustra la variación en la eficiencia de reflexión y la fase de la estructura de matriz simple al cambiar la longitud lateral de los hexágonos regulares para el rango de longitud de onda de 1000-1600 nm. Como se muestra en la Fig. 3a, b, hay muchos picos resonantes distinguibles en el espectro de reflexión. A través de la estructura de matriz simple, se puede realizar un cambio de fase de casi \ (\ pi \) para cada longitud de onda resonante. Está claro que se puede lograr un cambio de fase \ (2 \ pi \) completo cuando la longitud del lado del hexágono regular w cambia de 100 a 220 nm a una longitud de onda de 1529 nm. Para aclarar aún más el mecanismo del desplazamiento de fase \ (2 \ pi \), usamos el método de expansión electromagnética multipolar (EME) para calcular las secciones transversales de dispersión (SCS) de una nanovarilla de silicio hexagonal regular aislada [31, 41]. En la Fig. 3c, trazamos los SCS de dispersión calculados de los componentes dipolo eléctrico (ED), dipolo magnético (MD), cuadrupolo eléctrico (EQ) y cuadrupolo magnético (MQ) para w =160 nm. Obviamente, varias resonancias de Mie, especialmente las resonancias dipolares, se excitan en la longitud de onda operativa. Sin embargo, existen algunas desviaciones entre la excitación de las resonancias de Mie en la partícula aislada y la de las partículas periódicas. No hay un cambio de fase abrupto a una longitud de onda de 1529 nm, lo que prueba que el desplazamiento de fase \ (2 \ pi \) está formado por un solo modo. Por lo tanto, el mecanismo de control de fase \ (2 \ pi \) a una longitud de onda de 1529 nm se analiza mediante análisis en modo propio [42]. Estas nanovarillas pueden considerarse resonadores de Fabry-Pérot de factor de baja calidad, y la fase puede ser modulada por el índice de refracción efectivo del modo fundamental. Por lo tanto, se puede demostrar que la fase es

donde \ (H_1 \) es la altura de estas nanovarillas, \ (n _ {\ mathrm {eff}} \) es el índice de refracción efectivo del modo fundamental obtenido por el análisis de modo propio, y \ (\ lambda \) es la longitud de onda operativa . En la Fig. 3d, trazamos los perfiles de fase obtenidos mediante análisis de modo propio (línea discontinua) y simulación numérica (línea continua) a longitudes de onda de 1300 nm y 1529 nm, respectivamente. Como se muestra en la Fig. 3d, hay dos reducciones de fase abruptas en la fase simulada a una longitud de onda de 1300 nm, correspondientes a dos tipos de resonancias Mie. Cuando w cambia de 100 a 250 nm, las tendencias de cambio de fase obtenidas por los dos métodos son básicamente las mismas a una longitud de onda de 1529 nm. De acuerdo con el corrimiento al rojo de los picos de reflexión en la Fig. 3a, cuando w es superior a 250 nm, la resonancia de Mie se excita a una longitud de onda de 1529 nm. Para la metasuperficie que proponemos en este trabajo, dado que los parámetros estructurales de cada elemento están en el rango de 100 a 220 nm, como se muestra en la Tabla 1, no se excitan resonancias Mie dentro de este rango. Por lo tanto, podemos asumir que el cambio de fase se basa principalmente en la resonancia de Fabry-Pérot [6, 39, 40, 42]. De acuerdo con la ley de Snell generalizada, se puede lograr una transmisión anómala si una metasuperficie tiene una capacidad de cambio de fase \ (2 \ pi \). Ajustando el tamaño de las nanovarillas para que el cambio de fase esté espaciado uniformemente y cubra un rango \ (2 \ pi \) completo, podemos desviar el haz dislocando su frente de onda. La Figura 3e ilustra el diagrama esquemático de la metasuperficie de gradiente de fase. Seis nanobarras de silicio de diferentes tamaños con intervalos de fase \ (2 \ pi / 5 \) se disponen sobre un sustrato de sílice para formar un gradiente de fase completo de 0 a \ (2 \ pi \). El cuadro violeta representa un período completo y \ (P_x \) y \ (P_y \) se establecen en 3000 nm y 500 nm, respectivamente.

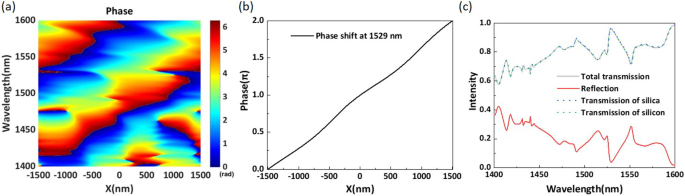
un Cambio de fase simulado de la metasuperficie a lo largo de la x -dirección en un período completo para el rango de longitud de onda de 1400–1600 nm. b Distribución de fase simulada a lo largo de x -dirección a una longitud de onda de 1529 nm. c Intensidades simuladas de la luz transmitida y reflejada

Resultados y discusión

La Tabla 1 muestra los parámetros estructurales de cada elemento para la estructura propuesta. Investigamos la distribución de fase y la intensidad de la luz de transmisión. Para facilitar el análisis, establecemos el origen de las coordenadas como el centro de la supercélula. Simulamos la distribución de fase de la luz de transmisión en el rango de longitud de onda de 1400 a 1600 nm. Como se muestra en la figura 4a, la estructura propuesta puede realizar un cambio de fase \ (2 \ pi \) completo en el rango de 1400-1600 nm. Para aclarar esto, la Fig. 4b muestra la curva de desplazamiento de fase a una longitud de onda central de 1529 nm. Como se muestra en la Fig. 4b, el cambio de fase muestra una tendencia lineal y es muy suave. De acuerdo con la ley de Snell generalizada, cuanto mejor es la linealidad del desplazamiento de fase, más plano es el plano de fase del equipo de la luz transmitida. Simulamos la transmitancia y la reflectancia de la metasuperficie propuesta para el rango de 1400-1600 nm, cuyos resultados se muestran en la figura 4c. Al observar la curva, podemos ver que la transmisión total sigue siendo altamente eficiente, superando el 60% en todo el rango de longitud de onda operativa. A una longitud de onda de 1529 nm, la eficiencia de transmisión total alcanza el 96,5% con una eficiencia de reflexión del 3,4%. La suma de la reflectividad de la estructura y la transmitancia del sustrato de sílice es 1 en todo el rango de longitud de onda. Por lo tanto, podemos determinar que la reflexión ocurre principalmente en la primera interfaz entre el aire y el sustrato. Como se muestra en la Fig. 4c, las diferencias entre las tres curvas de transmisión son apenas perceptibles y son causadas por la absorción de la estructura. La tasa de absorción es mucho menor al 0,1% porque la parte imaginaria del índice de refracción del silicio en el rango de longitud de onda del infrarrojo cercano es muy pequeña. Por tanto, la tasa de absorción es insignificante. La eficiencia de transmisión y la eficiencia de reflexión exhiben tendencias opuestas a la de la longitud de onda, y la pérdida de la estructura proviene principalmente de la reflexión. Está claro que la metasuperficie de gradiente de fase propuesta puede realizar un cambio de fase \ (2 \ pi \) casi lineal completo y, al mismo tiempo, mantener una mayor eficiencia de transmisión en el rango de 1400-1600 nm.

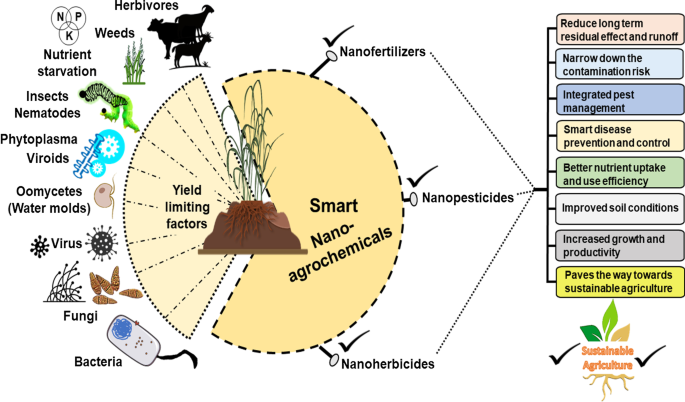
un Intensidad simulada de la eficiencia de transmisión anómala. b Eficiencia de transmisión de campo lejano para diferentes ángulos de refracción anómalos a una longitud de onda de 1529 nm. c Distribución de fase de la configuración de metasuperficie a una longitud de onda de 1529 nm. El ángulo de la figura muestra el ángulo de refracción de la luz transmitida anómala

Como se muestra en la Fig. 5a, también calculamos la eficiencia de transmisión anómala deseada de la metasuperficie de gradiente de fase en todo el rango de longitud de onda operativa y la normalizamos a la energía de la luz incidente. Comparando la Fig. 4c con la Fig. 5a, podemos ver que las tendencias de la eficiencia de transmisión total y la eficiencia de transmisión anómala con la longitud de onda son consistentes. Los resultados muestran que la eficiencia de transmisión anómala deseada excede el 80% en los rangos de longitud de onda de 1527-1545 y 1591-1600 nm. Sorprendentemente, la eficiencia de transmisión anómala es tan alta como del 96,2% a una longitud de onda de 1529 nm. La Figura 5b muestra la relación entre la eficiencia de transmisión de campo lejano y el ángulo de refracción anómalo a una longitud de onda de 1529 nm. Está claro que la energía de campo lejano de la luz transmitida se concentra principalmente en un ángulo de 30,64 y solo la energía débil se distribuye en los otros dos ángulos. Para facilitar la observación, la Fig. 5c muestra la distribución de fase de la configuración de la metasuperficie en la longitud de onda central. En la Fig. 5c, podemos ver que la luz transmitida es obviamente refractada y que el frente de onda es relativamente plano. Sustituyendo la longitud de onda de trabajo y el período de la estructura en la ecuación. (3), obtenemos un ángulo de transmisión anómalo \ (\ theta _r \) de 30,642, que está muy cerca de los resultados de nuestra simulación. Para verificar la relación entre el número de órdenes de difracción y la relación entre la longitud de onda y el período, establecemos \ (\ lambda _0 \) / \ (P_x \) en el valor crítico de 0.5 y seleccionamos cinco longitudes de onda diferentes para realizar cálculos teóricos. y simulaciones FDTD. Los resultados se muestran en la Tabla 2. Obviamente, los resultados de la simulación son muy consistentes con los resultados calculados.

De acuerdo con los ángulos calculados y simulados para la estructura propuesta que se muestran en la Tabla 2, cuando \ (\ lambda _0 \) / \ (P_x \) es mayor que 0.5, solo están presentes el orden de difracción 0 y el orden de difracción 1, y no hay orden de difracción 2. Cuando \ (\ lambda _0 \) / \ (P_x \) es menor que 0.5, los órdenes de difracción 0, 1 y 2 se obtienen en la simulación. Este resultado está completamente de acuerdo con el análisis teórico descrito anteriormente y, por lo tanto, confirma completamente la confiabilidad de la ley de Snell generalizada combinada con la teoría de la red.

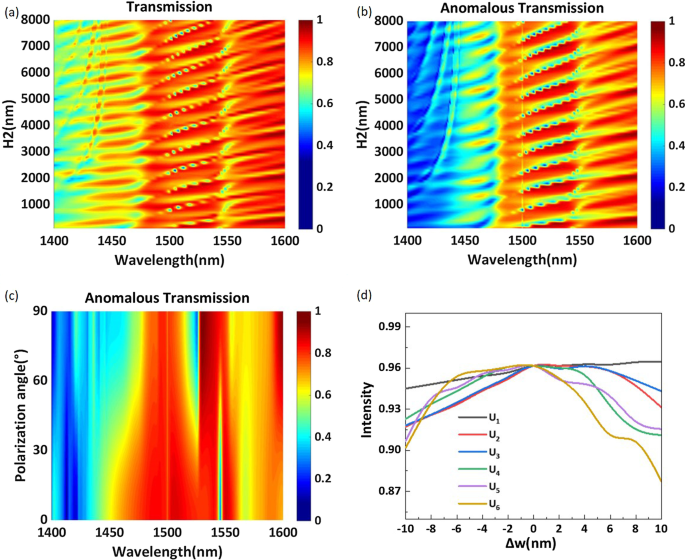
un La eficiencia de transmisión total y b la eficiencia de transmisión anómala en función del espesor del sustrato para el rango de longitud de onda de 1400 a 1600 nm. c La eficiencia de transmisión anómala de la estructura propuesta para diferentes ángulos de polarización en el rango de longitud de onda de 1400-1600 nm. d Eficiencia de transmisión anómala calculada a diferentes valores de la longitud del lado w

En la Fig. 6a, b, el rango de longitud de onda es de 1400 a 1600 nm, y la eficiencia de transmisión total y la eficiencia de transmisión anómala se grafican en función del espesor del sustrato \ (H_2 \). La eficiencia de transmisión se ve afectada por el grosor del sustrato y la longitud de onda máxima se desplaza al rojo al aumentar el grosor. Es obvio que tanto la eficiencia de transmisión total como la eficiencia de transmisión anómala cambian periódicamente al aumentar el espesor del sustrato. Para reducir el consumo de memoria en la simulación por computadora, el grosor del sustrato optimizado se establece en 7050 nm y la eficiencia de transmisión anómala deseada alcanza el 96,2% a una longitud de onda de 1529 nm. Creemos que se puede obtener una alta eficiencia de transmisión anómala incluso si el sustrato es grueso. También calculamos la variación en la eficiencia de transmisión anómala con el ángulo de polarización de la luz incidente, como se muestra en la Fig. 6c. A una longitud de onda de 1529 nm, la eficiencia de transmisión anómala aumenta con el aumento del ángulo de polarización y alcanza un máximo cuando el ángulo de polarización es de 90 ( y -polarización). Considerando que la longitud del lado w de la estructura requiere valores numéricos precisos y puede ser difícil de fabricar con precisión, calculamos la eficiencia de transmisión anómala a diferentes valores de w para probar la tolerancia de la estructura. Como se muestra en la Fig. 6d, la tolerancia de la estructura se obtiene cambiando la longitud del lado w basado en los parámetros estructurales enumerados en la Tabla 1. Estas curvas, \ (U_1 \) - \ (U_6 \), representan la variación en la eficiencia de transmisión anómala con las longitudes de los lados de las seis nanovarillas por intervalo periódico. El eje horizontal \ (\ Delta w \) representa la diferencia entre la longitud del lado simulado y la longitud del lado enumerada en la Tabla 1. Podemos ver que la curva \ (U_1 \) es muy plana y que la eficiencia de transmisión anómala cambia solo en 2 % con la longitud lateral dentro de un ancho de banda de 20 nm. Las tendencias de las curvas \ (U_2 \), \ (U_3 \), \ (U_4 \) y \ (U_5 \) son básicamente las mismas, y se puede obtener una eficiencia de transmisión anómala superior al 90% cuando la longitud del lado está dentro de el ancho de banda de 20 nm. Obviamente, cambiar la longitud del lado de \ (U_6 \) tiene la influencia más notable en el rendimiento; sin embargo, \ (U_6 \) todavía exhibe una alta eficiencia de transmisión anómala. Cuando la longitud del lado se reduce en 10 nm, la eficiencia de transmisión anómala permanece por encima del 90%. Cuando la longitud del lado aumenta en 10 nm, la eficiencia de transmisión anómala se ve notablemente afectada, pero aún supera el 87%. Estos resultados demuestran que un pequeño error durante la fabricación no afecta sustancialmente el rendimiento de la metasuperficie.

Puede verse en la ecuación. (3) que el ángulo de difracción de la luz de transmisión anómala se ve afectado por \ (\ lambda _0 \) / \ (P_x \); por lo tanto, intentamos cambiar la magnitud de \ (P_x \) para obtener diferentes ángulos de refracción anómalos. Un método eficaz para realizar diferentes ángulos de refracción anómalos es cambiar el número de elementos por intervalo periódico. Por lo tanto, seguimos diseñando metasuperficies de gradiente de fase con múltiples conjuntos. Los elementos de la metasuperficie por intervalo periódico cambian de tres a nueve. Seleccionamos la longitud de onda de trabajo con la mayor eficiencia de transmisión anómala para cada grupo de metasuperficies y observamos la distribución de fase de la luz transmitida. Los resultados de la simulación se grafican en la Fig. 7a-f. A medida que el número de elementos disminuye de nueve a tres, la relación de \ (\ lambda _0 \) / \ (P_x \) aumenta gradualmente y el ángulo de transmisión anómalo aumenta de 19,35 a 68,58. La Figura 7a-f muestra que las metasuperficies de gradiente de fase con diferentes elementos pueden realizar distribuciones de fase casi lineales y que el frente de onda de la luz transmitida es relativamente suave. Llevamos a cabo un análisis de campo lejano de las configuraciones anteriores y trazamos la distribución de energía de la luz transmitida a lo largo de cada ángulo de difracción, como se muestra en la Fig. 8a-f. Podemos obtener más del 80% de eficiencia de transmisión anómala de 19,35 a 46,68. Los parámetros estructurales de cada elemento y los resultados numéricos detallados se enumeran en la Tabla 3. En nuestro proceso de optimización, la longitud del lado del hexágono regular w y el período P son los principales parámetros de optimización.

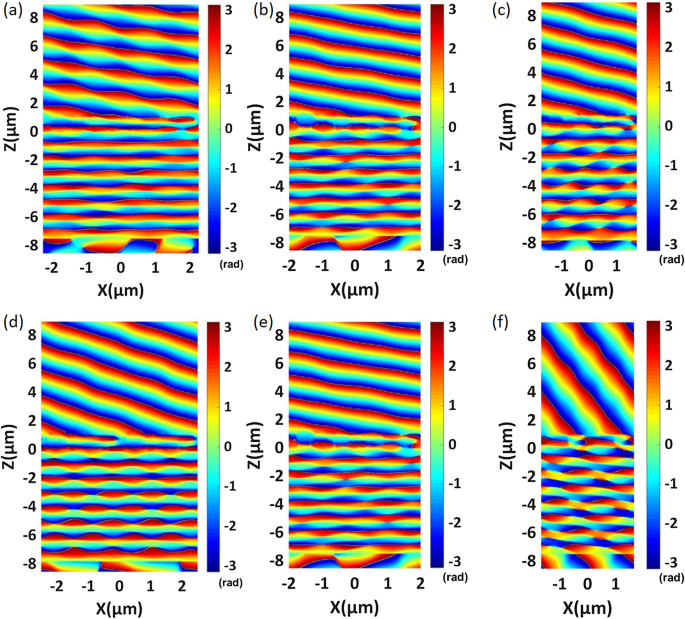
Distribución de fase de una metasuperficie de gradiente de fase que consta de diferentes números de elementos. un Metasuperficie de nueve elementos. b Metasuperficie de ocho elementos. c Metasuperficie de siete elementos. d Metasuperficie de cinco elementos. e Metasuperficie de cuatro elementos. f Metasuperficie de tres elementos. d - f representan dos períodos para mostrar mejor el efecto de transmisión anómalo. Los parámetros detallados se muestran en la Tabla 3

Intensidades de transmisión de campo lejano en diferentes ángulos de metasuperficies de gradiente de fase que constan de diferentes números de elementos. un - f representan nueve, ocho, siete, cinco, cuatro y tres elementos, respectivamente

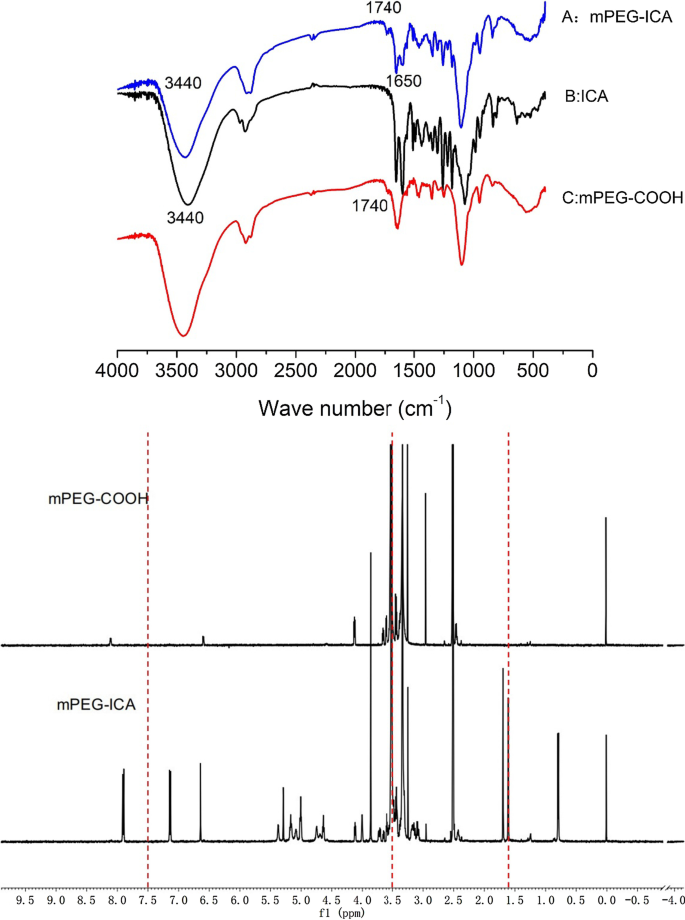
un Variación de fase simulada de la metasuperficie de ángulo grande a lo largo de x -dirección en un período completo para longitudes de onda de 1400–1600 nm. b Desplazamiento de fase \ (2 \ pi \) completo a lo largo de x -dirección de la metasuperficie de gradiente de fase para 1450, 1500, 1536 y 1550 nm. c La intensidad de la transmisión total y la transmisión anómala

De acuerdo con la ley de Snell generalizada, para diseñar un ángulo de refracción anómalo mayor \ (\ theta _r \), debemos aumentar la relación entre la longitud de onda de trabajo \ (\ lambda \) y el período estructural \ (P_x \). As shown in Fig. 9a, we plot the phase variation of the transmitted light along the x -direction for wavelengths of 1400–1600 nm. For clarity, we select four wavelength points, i.e., 1450 nm, 1500 nm, the central working wavelength 1536 nm, and 1550 nm, to plot the phase shift curves shown in Fig. 9b. It is clear that the all-dielectric metasurface can realize a full \(2\pi\) phase shift for the wavelength points. From Fig. 9b, we can see that the phase variation shows a linear trend along the x -direction. We calculate the total transmission efficiency and the desired anomalous transmission efficiency of the structure in the working band, the results of which are shown in Fig. 9c. It can be observed that the total transmission efficiency is lower than before. However, at the operating wavelength of 1536 nm, the anomalous transmission efficiency can reach 69.6% with an anomalous refraction angle of 68.58. The phase distribution of transmitted light and the energy distributions at different anomalous refraction angles are shown in Figs. 7f and 8f, respectively. From the electric field distribution, we can clearly see that the equilateral phase plane of the transmitted light is very flat. The transmitted light emits very little energy at 0 and \(-68.58\), and the majority of transmitted light is concentrated at 68.58. The anomalous transmission performance of the all-dielectric phase-gradient metasurface designed by us is better than that of most of the metasurface structures proposed before, and the anomalous transmission efficiency can reach more than 60% within the range of anomalous refraction angles from 0 to 70. Based on the above analysis, an anomalous refraction angle of approximately 30 is the most reasonable. At this anomalous refraction angle, the highest anomalous transmission efficiency can be achieved, and the anomalous refraction angle can be guaranteed to be large enough.

Conclusions

In summary, we designed and numerically investigated an all-dielectric phase-gradient metasurface to achieve high-efficiency anomalous transmission in the near-infrared region. The metasurface consists of regular hexagonal silicon nanorods arranged on a silica substrate. The FDTD method was used to calculate the transmission efficiency and anomalous refraction angle of the transmitted light. The results show that the metasurface can realize a complete \(2\pi\) phase shift in the wavelength range of 1400–1600 nm. At a center wavelength of 1529 nm, the desired anomalous transmission efficiency reached 96.2% with an anomalous refraction angle of 30.64. Furthermore, the anomalous transmission efficiency exceeded 80% in the range of 1527–1545 nm, which means that our design is more flexible. We also designed multiple sets of phase-gradient metasurfaces by changing the number of elements per periodic interval and adjusting the period of the metasurface. The optimized results show that we can modulate the anomalous refraction angle in the range of 19.35-68.58. When the anomalous refraction angle is less than 46.68, more than 80% of the anomalous transmission efficiency can be obtained. Such an all-dielectric metasurface will be easy to apply to integrated optical devices.

Disponibilidad de datos y materiales

The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

Abreviaturas

FDTD:

Finite difference time domain

TE:

Transverse electric

LPCVD:

Low-pressure chemical vapor deposition

EBL:

Electron beam lithography

PEC:

Proximity effect correction

EME:

Electromagnetic multipole expansion

SCSs:

Scattering cross sections

ED:

Electric dipole

MD:

Magnetic dipole

EQ:

Electric quadrupole

MQ:

Magnetic quadrupole

Impacto de los estados de la superficie y la fracción molar de aluminio en el potencial de la superficie y 2DEG en los HEMT de AlGaN / GaN Control completo de polarización de terahercios con ancho de banda ampliado a través de metauperficies dieléctricas