Impacto de los estados de la superficie y la fracción molar de aluminio en el potencial de la superficie y 2DEG en los HEMT de AlGaN / GaN
Resumen
La presencia de trampas superficiales es un fenómeno importante en AlGaN / GaN HEMT. Las propiedades eléctricas y físicas de estas trampas de superficie se han analizado mediante el estudio de la concentración de electrones 2DEG junto con la variación del porcentaje de aluminio en la capa de barrera de HEMT. Este análisis muestra que de donantes profundos a superficiales, el cambio porcentual en la densidad de electrones en 2DEG se satura (cerca del 8%) con el cambio en la concentración de aluminio. También se analiza la profundidad del potencial cuántico muy por debajo del nivel de Fermi y se encuentra que se satura (cerca del 2%) con porcentaje de aluminio cuando el donante de superficie indica que la energía cambia a profunda de superficial. La física detrás de este efecto colectivo también se analiza a través del diagrama de bandas. El efecto de las trampas de donantes de superficie sobre el potencial de superficie también se ha discutido en detalle. Estos estados superficiales se modelan como estados donantes. Donante profundo ( E C - E D =1,4 eV) a un donante superficial ( E C - E D =0,2 eV) las trampas de superficie se estudian a fondo para la concentración de donantes de 10 11 a 10 16 cm −2 . Este estudio implica una variación de la concentración de aluminio del 5 al 50%. Este artículo presenta por primera vez el estudio TCAD completo del donante de superficie y el análisis de la concentración de electrones en el canal y la formación de 2DEG en la interfaz AlGaN-GaN.
Introducción
Las aplicaciones de alta frecuencia y alta potencia son los dos rasgos principales del material GaN que se han estudiado en las últimas tres décadas [1, 2]. Una de las principales ventajas de la estructura AlGaN / GaN es la formación de 2DEG en el pozo de potencial triangular en la interfaz AlGaN-GaN incluso sin dopaje intencional en la capa de barrera [3, 4]. Está bien probado que existe polarización espontánea y piezoeléctrica en la capa AlGaN de la estructura AlGaN / GaN [3]. Esta polarización da como resultado dos hojas opuestas de cargas en la parte inferior y superior de la capa de barrera de AlGaN. Estas cargas de la hoja de polarización por sí solas no son suficientes para formar un pozo de potencial triangular en la interfaz AlGaN-GaN. Para abordar esto, Ibbetson et al . [5] sugirió que debería haber una capa positiva de cargas que debe existir en la superficie de la capa de AlGaN. Estas cargas positivas surgen debido a la ionización de los estados donantes de la superficie (1,42 eV de la banda de conducción con 1,35 × 10 13 cm −2 ) en la superficie [6].
Vetury y otros . [7] investigó el efecto de estos estados superficiales utilizando sondas potenciales como puerta flotante. Se ha estudiado el efecto de los estados de la superficie en el rendimiento de CC y RF de AlGaN / GaN HEMT [8, 9]. El comportamiento de la puerta Schottky a escala nanométrica analiza la formación de la puerta virtual en la región no cerrada debido a los estados donantes de superficie [10]. Los estados donantes de superficies fijas se utilizan para analizar el efecto de autocalentamiento en HEMT [11]. Longobardi y otros . [12] realizó la primera simulación TCAD para estudiar el efecto de los estados donantes de superficie sobre las características de DC de los MISFET de AlGaN / GaN. Para activar estos estados donantes de superficie en la simulación TCAD, Bakeroot y otros introdujeron un modelo diferente [13, 14]. Las resistencias de drenaje / fuente también dependen del sesgo de la puerta debido a la formación de la puerta virtual en la región no cerrada de la superficie de AlGaN. Pradeep y otros . [15] han desarrollado el procedimiento de extracción de movilidad y resistencia basado en las características de CC de región lineal de AlGaN / GaN HEMT. Meneghesso y otros . [16] discutió el estado de la superficie como una trampa que captura la capa de agujeros altamente densa en la superficie de AlGaN para compensar los electrones en 2DEG. Las trampas de donantes de superficie disponibles en la parte superior de la capa de AlGaN alteran el comportamiento eléctrico del dispositivo cuando estas trampas están ocupadas por electrones con polarización de puerta negativa [17]. La relación entre las trampas de donantes de superficie y los electrones 2DEG también se ha discutido mediante la simulación TCAD mediante la adopción de fenómenos de transporte dependientes del tiempo [18]. Aunque se han explorado diferentes técnicas de caracterización, Tapajna et al. [19] utilizó el método de umbral transitorio para investigar las trampas aceptoras de interfaz, pero la caracterización de las trampas donantes de superficie aún no se ha explorado. También se ha discutido un amplio enfoque de modelado computacional para la trampa de superficie como donante [20]. Gucmann y otros . [21] discutió que si la densidad del donante de superficie es mayor que la concentración de carga de polarización, entonces los electrones se transfieren a la interfaz AlGaN-GaN para originar el 2DEG en el canal.
La literatura discutida anteriormente ha informado sobre muchos aspectos relevantes de la heteroestructura de AlGaN / GaN, pero no tiene en cuenta el efecto combinado del donante de superficie (concentración + energía) y la contribución de la concentración de aluminio en la concentración de electrones bidimensionales. Es evidente que el porcentaje de aluminio es el principal responsable de la carga de polarización en la capa de barrera de AlGaN [3].
Para proporcionar una comprensión física adecuada de tal efecto, hemos cubierto después de la investigación en el presente trabajo (i) el efecto sobre la concentración de electrones bidimensionales con cambios de trampa de donantes de superficie de profunda a superficial junto con cambios de porcentaje de aluminio en la capa de barrera AlGaN, (ii) el efecto de la trampa de superficie y el porcentaje de aluminio sobre el potencial de superficie y (iii) la influencia de la trampa del donante de superficie y el porcentaje de aluminio en el pozo de potencial triangular en la interfaz AlGaN-GaN.
Sección de método y configuración de simulación
Las simulaciones de dispositivos 2-D se llevaron a cabo utilizando Sentaurus TCAD versión L-2016.12 de Synopsys [22]. Calibramos la configuración de simulación TCAD reproduciendo el resultado experimental de la heteroestructura de AlGaN / GaN HEMT [15], como se muestra en la Fig. 1b.
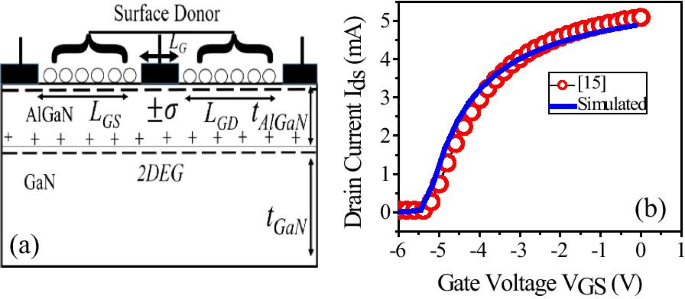
un Esquema de estructura simulada en 2D con fracción molar de Al de 28%. b Calibración de la configuración de simulación mediante la reproducción de los resultados experimentales informados [15]
El dispositivo calibrado tiene una capa de barrera de AlGaN de 30 nm en la parte superior de la capa tampón de GaN de 2 μm. Longitud de la puerta Schottky ( L G ) de 1 μm se coloca simétricamente en la parte superior de la capa de barrera de AlGaN. Región sin compuerta desde la puerta hasta el drenaje / fuente ( L GD / L GS ) tiene una dimensión de 2,5 μm cada uno y el ancho del dispositivo es de 150 μm.
La plataforma de simulación aborda tres condiciones (condición de Poisson junto con la condición de continuidad de electrones y huecos) que supervisa el comportamiento de los semiconductores.
También se incluye el modelo de transporte de deriva y difusión (DD) autoconsistente. Se invocó la movilidad Lombardi y el modelo de movilidad unificada de Philip para facilitar la degradación de la movilidad debido al campo eléctrico y al dopaje. Además, se utilizó el modelo de recombinación Auger y SRH (Shockley-Read-Hall) junto con las estadísticas de Fermi-Dirac. El modelo Slotboom se activa para encontrar el estrechamiento de la banda prohibida del drenaje muy dopado y el área extendida de la fuente. Dado que esta estructura tiene dos capas y estamos cambiando el porcentaje de aluminio en la capa de barrera de AlGaN, la carga de polarización se introduce según la ecuación de [3]:
$$ \ left | {\ sigma (x)} \ right | =\ left | {2 \ frac {a (0) - a (x)} {{a (x)}} \ left \ {{e_ {31} (x) - e_ {33} \ frac {{C_ {13} (x )}} {{C_ {33} (x)}}} \ right \} + P _ {{{\ text {SP}}}} (x) - P _ {{{\ text {SP}}}} (0 )} \ right | $$ (1)donde P SP es polarización espontánea, e 33 y e 31 son coeficientes piezoeléctricos, C 33 y C 31 son constantes elásticas, a es la constante de celosía y x es un porcentaje molar de aluminio.
La variación de la carga de polarización ± σ AlGaN ( x ) con porcentaje de aluminio se muestra en la Fig. 2a [3]. Una vez que se calcula la carga de polarización, se puede resolver la ecuación de Poisson. En la interfaz AlGaN-GaN, la banda de conducción cambia abruptamente y forma un pozo cuántico de potencial triangular estrecho (1-4 nm) donde se acumulan los electrones. Como este potencial cuántico es muy estrecho, la densidad reducida de los estados se vuelve dominante. La ecuación cuántica de Schrodinger explica bien el potencial cuántico, pero es difícil de resolver para un dispositivo HEMT más grande. Para capturar el comportamiento del pozo de potencial cuántico, invocamos el modelo eQuantumpotential en el Sentaurus TCAD que activa el modelo de corrección cuántica de gradiente de densidad [23] y da un resultado muy similar con la ecuación cuántica de Schrodinger para dispositivos HEMT más grandes (dispositivos HEMT de potencia). El modelo cuántico de gradiente de densidad reduce el valor pico de la densidad electrónica en 2DEG, y el valor pico también se aleja de la interfaz AlGaN-GaN. Por lo tanto, esto reduce el mecanismo de dispersión de la interfaz y mejora la movilidad en el canal, ver Fig. 2b [20]. El modelo cuántico de gradiente de densidad introduce un término adicional Λ en la fórmula de densidad normal como:
$$ n =N _ {{\ text {C}}} F_ {1/2} \ left ({(E _ {{\ text {F}}} - E _ {{\ text {C}}} - \ Lambda) / kT} \ derecha) $$ (2)donde N C es la densidad efectiva de estados, F 1 / 2 es la integral de Fermi de orden 1 / 2, E F es la energía cuasi-Fermi de los electrones, E C es el borde de la banda de conducción y kT representa la energía térmica de los electrones. Λ se calcula mediante:
$$ \ Lambda =- \ left ({\ left ({{{\ gamma \ hbar ^ {2}} \ mathord {\ left / {\ vphantom {{\ gamma \ hbar ^ {2}} {6m_ {n} " }}} \ right. \ kern- \ nulldelimiterspace} {6m_ {n}}}} \ right) \ cdot \ left ({\ nabla ^ {2} \ sqrt n} \ right) / \ sqrt n} \ right) $$ (3)donde ħ = h / 2 π , h es la tabla constante, m n es una masa efectiva del electrón, γ ( γ =1.28) es un parámetro de ajuste y n es la densidad de electrones.
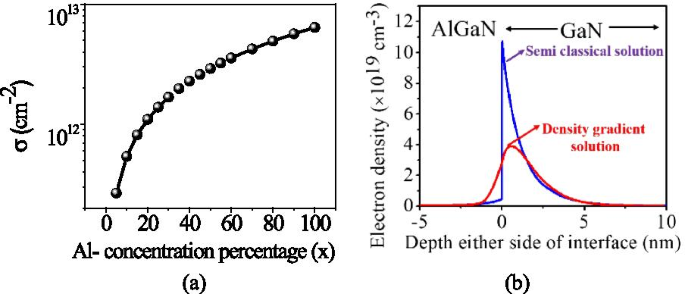
un Variación de la carga de la hoja de polarización con respecto a la concentración de aluminio en la capa de barrera de AlGaN [3]. b Efecto del cautiverio cuántico sobre la densidad de electrones 2DEG
Las trampas de superficie se introdujeron como estado donante (+ σ D ) sobre la superficie de las capas de barrera de AlGaN Fig. 1a, y la simulación se realizó a la temperatura de 300 K. La calibración se realizó con la concentración inicial de aluminio del 28%.
Resultados de la simulación y discusión
Efecto del porcentaje de aluminio y las trampas de superficie en la densidad 2DEG
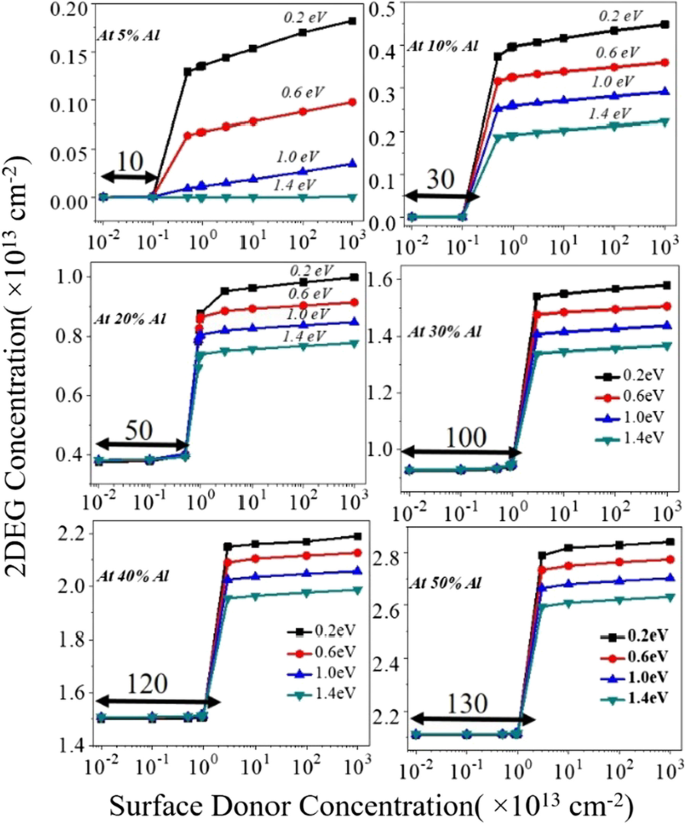
El dispositivo se simuló sin aplicar condiciones de polarización para investigar la densidad de electrones 2DEG. Mientras nos concentramos en la densidad de electrones 2DEG, para toda la energía del estado donante, hasta un cierto valor (valor relativamente más bajo) de concentración de trampa donante, no hay un cambio significativo en la densidad de electrones (es decir, Región1). La densidad de electrones 2DEG cambia proporcionalmente con la concentración del donante de superficie (entre la Región1 y la Región2). Después de un cierto valor umbral de la trampa del donante de superficie, nuevamente no aparece ningún cambio en la densidad de electrones (es decir, Región 2), ver Fig. 3a – d. Este mecanismo se puede explicar de la siguiente manera:
un - d Variación de la densidad de la hoja de electrones en 2DEG w.r.t, concentración de donante de superficie y energía (de 0,2 eV superficial a 1,4 eV profundo) para diferentes porcentajes de aluminio. e Diferente distribución de carga y orientación del campo eléctrico en el dispositivo
(i) La banda de conducción de la capa de barrera de AlGaN para la región 1 tiene un espacio mayor desde el nivel de Fermi en la superficie. A medida que la concentración de la trampa del donante comienza a aumentar de menor a mayor valor, en el período de transición (entre la Región1 a la Región2), la banda de conducción comienza a moverse proporcionalmente hacia el nivel de Fermi. Por lo tanto, la concentración de 2DEG comienza a aumentar de un valor más bajo a un valor más alto. En el período de transición (entre la Región1 a la Región2), la banda de conducción comienza a moverse proporcionalmente hacia el nivel de Fermi y, por lo tanto, la energía de la superficie donante también se mueve hacia el nivel de Fermi. Para la Región 2, una vez que la concentración del donante cruza el valor umbral, la flexión de la banda de conducción comienza de tal manera que la energía de la trampa del donante fija el nivel de Fermi. Debido al sustento del nivel de Fermi, todos los estados donantes se ionizan y contribuyen con electrones al pozo de potencial cuántico triangular 2DEG. Una vez que la energía de los estados donantes se fija al nivel de Fermi, no se refleja ningún cambio significativo en la densidad de electrones. (ii) Para encontrar la neutralidad de carga en el dispositivo, los estados donantes de superficie son esenciales para contrarrestar los electrones en 2DEG. A medida que aumentan los estados donantes de superficie, un campo eléctrico comienza a aumentar desde la superficie hasta el pozo cuántico 2DEG. Este campo eléctrico contrarresta el campo eléctrico incorporado producido por la carga de la hoja de polarización (± σ AlGaN ). Cuando el campo eléctrico externo comienza a exceder el campo eléctrico interno (debido a ± σ AlGaN ), reduce la banda de conducción en la superficie y, por lo tanto, aporta más electrones al pozo de potencial 2DEG, ver Fig. 3e. Cuando el porcentaje de aluminio aumenta del 5 al 50%, la densidad de carga de la hoja de polarización también aumenta proporcionalmente, lo que conduce a un campo eléctrico interno elevado (debido a la polarización). Para superar este campo eléctrico interno, se requiere una mayor concentración de trampas donantes de superficie. Por lo tanto, la región de transición se desplaza (de 10 a 130 veces con 10 11 cm −2 ) para el valor más alto de la concentración de la trampa del donante, donde la densidad de electrones 2DEG cambia proporcionalmente a la concentración de la trampa del donante, Fig. 3a – d. La concentración de 2DEG para cada porcentaje de aluminio con respecto al donante de superficie (concentrado + energía) se representa en la Fig. 4. A pesar de que el patrón de concentración de electrones de 2DEG es el mismo para todos los porcentajes de aluminio cuando la trampa del donante pasa de poco profunda (0.2 eV) a profundo (1.4 eV) (Fig. 5), el cambio en la densidad de electrones 2DEG de profundo a poco profundo sigue siendo bastante significativo. En el caso de una concentración de aluminio al 5%, la trampa donante va de profunda (1.4 eV) a poco profunda (0.2 eV), no contribuye significativamente al pozo potencial. Como concentración de carga de polarización (± σ ) es del orden de 10 11 cm −2 Para aluminio al 5% ver Fig. 2a, el campo eléctrico debido a estas cargas de polarización no es suficiente para desplazar la banda de conducción por debajo del nivel de Fermi, por lo que no se forma un pozo de potencial triangular 2DEG en el lado GaN de la estructura de la interfaz AlGaN-GaN. También es evidente que incluso para la mayor concentración de trampas de donantes de superficie, la saturación de la densidad de electrones no ocurre como se muestra en las Figs. 4a y 6. Esto también es cierto para el porcentaje de aluminio del 10% como se muestra en la Fig. 4b. Para 20% y más, la concentración de carga de polarización (± σ) es mayor que 10 12 cm −2 . Por lo tanto, el campo eléctrico interno es lo suficientemente grande como para hacer que la banda de conducción se desplace por debajo del nivel de Fermi y, por lo tanto, forma el potencial cuántico triangular 2DEG. Ver Fig. 6b, c. Entonces, para un porcentaje de aluminio del 20% o superior, la densidad de electrones 2DEG se acerca a ~ 10 13 cm −2 para trampas de donantes poco profundas como se muestra en la Fig. 4c. Para concentraciones de aluminio del 20%, 30% y más, la contribución del electrón en el pozo triangular tiene una densidad de 1 × 10 13 a 3 × 10 13 cm −2 . La Figura 5a, b muestra el cambio porcentual de la densidad de electrones en el pozo triangular cuando la energía de la trampa donante cambia de 1.4e a 0.2 eV. A medida que pasamos del porcentaje de aluminio del 5 al 50%, el cambio en la concentración de 2DEG se reduce significativamente de 10,89 veces a 1,08 veces y se satura más allá del 30%.
Variación de un porcentaje de aluminio individual a la trampa de la superficie donante de profundo a poco profundo con respecto a la banda de conducción

un Cambio porcentual de la escala logarítmica en la densidad de electrones 2DEG para la concentración de Al cuando el donante de superficie se vuelve poco profundo desde el nivel profundo con respecto a la banda de conducción. b Escala lineal
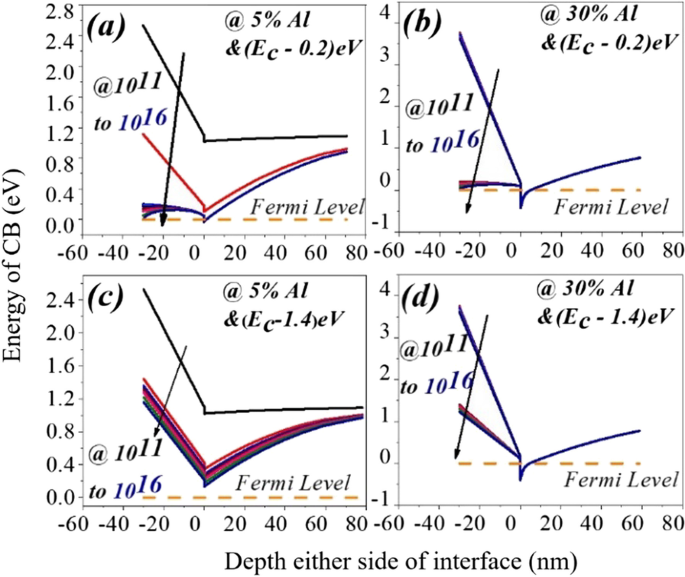
un , c Variación de la banda de conducción a ambos lados de la interfaz AlGaN-GaN para aluminio al 5% y b , d para 30% de aluminio. La trampa de superficie de nivel profundo no aporta electrones ni carga laminar positiva al pozo potencial ni a la superficie, lo que hace que la pendiente de la banda de conducción sea mayor. Incluso para el estado de la superficie del donante profundo (1,4 eV), existe un potencial de 2DEG que se está formando para un 30% de aluminio. Esto no es cierto para el 5% de aluminio
Efecto del porcentaje de aluminio y la trampa de superficie en el potencial de superficie
En algunas publicaciones se ha analizado la variación del potencial de superficie debido al cambio en el porcentaje de aluminio [29]. Pero no han incorporado el efecto de las trampas de donantes de superficie sobre el potencial de superficie. Aquí informamos la variación del potencial de superficie debido a las trampas de donantes de superficie, tanto en las dimensiones de energía como de concentración, ver Fig. 7a. En este estudio, hemos cambiado la concentración de donantes de superficie de 1 × 10 12 a 1 × 10 16 y energía donante de superficie de 0,2 a 1,4 eV. El potencial de superficie se ha calculado a partir de la Fig. 6b. El potencial de superficie se asienta cerca de 3,7 eV (para la concentración de donantes de superficie 1 × 10 12 ) y 3,6 eV (para la concentración de donantes de superficie 1 × 10 13 ). Este potencial de superficie no depende de la energía de la trampa donante de superficie por su valor más bajo. El potencial de superficie aumenta linealmente a medida que el donante de superficie va profundo (1,4 eV) desde poco profundo (0,2 eV). A medida que el potencial de superficie desciende, la concentración de electrones 2DEG aumentará porque el potencial de superficie varía linealmente con la energía de la trampa del donante de superficie. El porcentaje de aluminio también tiene un gran impacto en el potencial de la superficie. Al aumentar el porcentaje de aluminio del 5 al 50%, la concentración de electrones aumenta de 7,79 × 10 11 a 2,75 × 10 13 . El potencial de superficie también aumenta de 0,49 a 0,576 eV cuando el porcentaje de aluminio cambia de 5 a 50%, ver Fig. 7b. Por lo tanto, la concentración y la energía de la trampa del donante de superficie, junto con la concentración de aluminio, tienen una gran influencia en el potencial de la superficie.
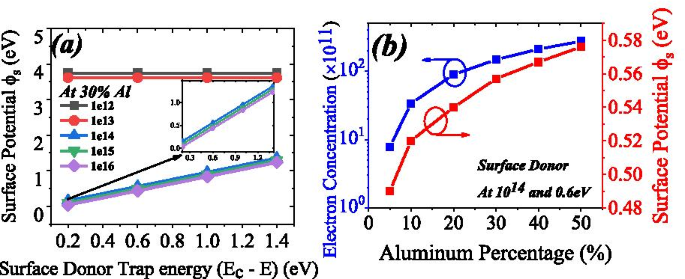
un Variación del potencial de superficie con respecto a la energía de la trampa donante de superficie. A concentraciones más bajas (menos de 1e14) no hay un cambio significativo en el potencial de superficie. Concentración de donante de superficie superior a 1e13, el potencial de superficie cambia proporcionalmente a la energía del donante de superficie. b La concentración de electrones en 2DEG cambia de 7,79 × 10 11 a 2,75 × 10 13 para cambios de porcentaje de aluminio del 5% al 50% (línea azul). El potencial de superficie cambia aproximadamente 0,1 eV del 5 al 50% del porcentaje de aluminio
Efecto del porcentaje de aluminio y la trampa de superficie en la banda de conducción y el pozo de potencial 2DEG
Las trampas de superficie ionizada aportan electrones al pozo de potencial y la carga laminar positiva en la superficie de AlGaN [6]. En el caso de una concentración de aluminio del 5%, a medida que las trampas se profundizan desde el nivel de energía superficial, la cantidad de trampas de superficie ionizada se vuelve cada vez más pequeña. Por lo tanto, las trampas de superficie ionizada contribuyeron con menos electrones al pozo de potencial triangular y a las cargas laminares positivas en la superficie. Una menor cantidad de cargas laminares positivas y concentración de electrones en 2DEG no aporta suficiente campo eléctrico externo y, por lo tanto, la pendiente de la banda de conducción en la capa de AlGaN se hace más grande como se muestra en la Fig. 6. Esto también es cierto para el aluminio con un 10% en capa barrera AlGaN. Los electrones libres de los estados donantes de superficie residen en el pozo de potencial 2DEG y neutralizan la carga laminar positiva que aparece en la superficie de AlGaN. Esta carga de la hoja de electrones se calcula mediante [24]:
$$ n _ {{\ text {s}}} (x) =\ frac {+ \ sigma (x)} {e} - \ left ({\ frac {{\ varepsilon_ {o} \ varepsilon (x)}} {{de ^ {2}}}} \ right) \ left [{e \ phi _ {{\ text {b}}} (x) + E _ {{\ text {F}}} - \ Delta E _ {{\ texto {C}}} (x)} \ right] $$ (4)donde d es el grosor del Al x Ga (1− x ) N capa de barrera, ϕ b es la barrera de Schottky, E F es el nivel de Fermi y Δ E C es el desplazamiento de la banda de conducción en la interfaz AlGaN-GaN. Es evidente a partir de la ecuación. (4) que la densidad de carga de la hoja de electrones es directamente proporcional al desplazamiento de la banda de conducción y a las cargas de polarización, que es una función del porcentaje de aluminio. A medida que aumentamos el porcentaje de aluminio del 10 al 50%, el desplazamiento de la banda de conducción aumenta [25] y, por lo tanto, la densidad de electrones en 2DEG aumenta debido al aumento en el número de niveles de energía, ver Fig. 8. El campo eléctrico interno del dispositivo, cuando la concentración de aluminio es del 20% o más, es tal que la pendiente de la banda de conducción es lo suficientemente alta como para construir el pozo de potencial triangular incluso para energía de trampa de superficie de nivel profundo (1.4 eV) y concentración de trampa de donante de superficie más baja como se muestra en la Fig. 6b, d .
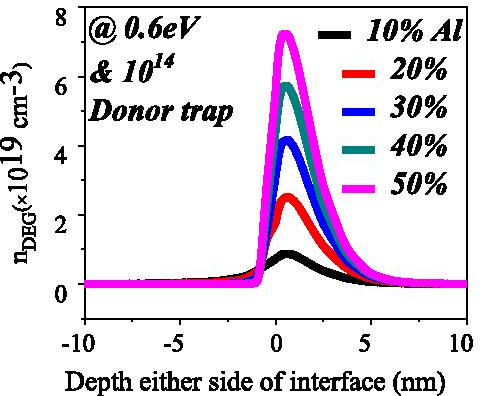
Densidad de electrones en pozo de potencial cuántico triangular para diferentes concentraciones de aluminio a una concentración y energía de donante fijo
Es importante observar la muesca del potencial cuántico triangular bien formado por debajo del nivel de Fermi (( E F - E) eV), donde E es la energía por debajo del nivel de Fermi. Dos parámetros importantes en el pozo de potencial cuántico triangular son la profundidad del potencial muy por debajo del nivel de Fermi y el ancho del pozo de potencial en el nivel de Fermi. El confinamiento de los electrones en regiones de dos dimensiones se denomina hoja cuántica 2DEG. La densidad de estados N ( E ) es una de las características importantes del pozo de potencial cuántico 2DEG. La densidad de estados en pozo cuántico bidimensional se define como [26]:
$$ N (E) =\ left ({{{m ^ {*} L _ {{\ text {X}}} ^ {2} E} \ mathord {\ left / {\ vphantom {{m ^ {*} L _ {{\ text {X}}} ^ {2} E} {\ pi \ hbar ^ {2}}}} \ right. \ Kern- \ nulldelimiterspace} {\ pi \ hbar ^ {2}}}} \ derecha) $$ (5)donde m * es la masa efectiva del electrón y L X es el ancho del pozo. Esta densidad de estado en un pozo bidimensional parece una función escalonada.
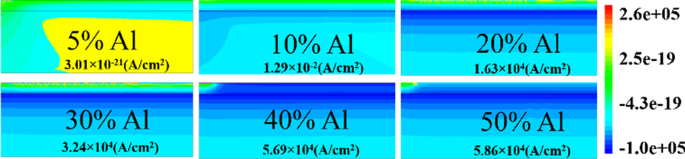
El número de estados ocupados depende del nivel de Fermi. Por ejemplo, si el nivel de Fermi es superior a E 1 pero menos de E 2 ; entonces solo E 1 la subbanda está llena. Si el nivel de Fermi está por encima de E 2 , pero menos de E 3 , luego dos subbandas inferiores E 2 y E 1 están llenos de electrones como se muestra en la Fig. 9b. Esto significa que si la energía en la interfaz es más profunda con el nivel de Fermi, solo se esperarán electrones en gran número. En la heteroestructura de AlGaN / GaN, el espaciado de energía disminuye (( E 2 - E 1 )> ( E 3 - E 2 )) para subbandas superiores [27]. A medida que aumenta la energía de subbanda, la diferencia entre ellos se vuelve insignificante y parece continua. La solución rigurosamente correcta de la función de onda contiene la ecuación de Poisson y la ecuación de Schrodinger simultáneamente. Pero el modelo de gradiente de densidad genera aproximadamente el mismo resultado con la ecuación de Schrodinger. En el pozo de potencial cuántico, el nivel de energía se cuantifica porque este pozo forma longitudes de hasta unos pocos nm en el lado GaN de la interfaz AlGaN-GaN. La muesca más profunda por debajo del nivel de Fermi ciertamente tendrá un mayor número de niveles de energía cuantificados. El nivel de energía cuantificado por debajo del nivel de Fermi está ocupado. Por tanto, cuanto más profunda sea la energía por debajo del nivel de Fermi, la concentración de electrones será mayor en 2DEG. De la Fig. 9a, está claro que el nivel de energía por debajo del nivel de Fermi aumenta cuando aumenta el porcentaje de aluminio porque aumenta la carga de polarización y, por lo tanto, el campo eléctrico interno hace que la muesca sea más profunda. En lo que respecta a la energía de los donantes de superficie, se desprende de la discusión anterior que cuando las trampas de la superficie son más profundas (1,4 eV), la ionización de estos donantes de superficie se reduce. Por lo tanto, el campo eléctrico se genera debido a cargas laminares positivas en la superficie y los electrones aportados por estos donantes de superficie a 2DEG no son suficientes para superar el campo eléctrico interno. Por lo tanto, el efecto de la carga de polarización en términos de campo eléctrico se reduce, lo que conduce a menos niveles de energía por debajo del nivel de Fermi. Una excepción es para la concentración de aluminio al 5%, se desprende de la Fig. 10a que el valor de E F - E es negativo ya que se supone que el nivel de Fermi es cero, para las trampas de donantes profundos (> 0,9 eV a 1,4 eV), lo que significa que la energía E es superior al nivel de Fermi (no se forma 2DEG). Para trampas donantes de superficie menos profundas (<0,9 eV a 0,2 eV), el valor de E F - E es positivo, lo que significa que el valor de E es más bajo que el nivel de Fermi. Para el resto de la concentración de aluminio (10% a 50%), el valor de E F - E es positivo, lo que significa que el valor de E es más bajo que el nivel de Fermi y se está formando una muesca 2DEG para todos los tipos de energía donante de superficie (de 0,2 eV a 1,4 eV). Se observa en la Fig. 11a que el cambio porcentual de energía E con aluminio se satura más allá del 20% de concentración de aluminio, lo que también está en sintonía con la Fig. 5. La profundidad de la muesca por debajo del nivel de Fermi no cambia significativamente después de una concentración de aluminio del 20% cuando el donante de superficie atrapa el cambio de energía de profundo a poco profundo. La Figura 11b también muestra que no hay una corriente significativa hasta el 10% de fracción molar de aluminio. Más allá del 10% hay un cambio significativo en la corriente cuando la energía del donante de superficie cambia de E C - 0,2 a E C - 1.4 eV y saturado más allá del 20% nuevamente. Este resultado también está en sintonía con las Figs. 11a y 5. El gráfico de contorno de la densidad de corriente absoluta también muestra que se satura por encima del 20% de fracción molar de Al y sin densidad de corriente significativa hasta el 10% de la fracción molar de Al Fig. 12. Esto también valida la no formación de 2DEG hasta el 10% de Al fracción molar. Una cantidad significativa de densidad de electrones observada por encima del 20% de la fracción molar Fig. 13a. La distribución del campo eléctrico a lo largo del canal se representa en la Fig. 13b. La Figura 13b muestra que no hay un campo eléctrico notablemente mejorado debajo de la puerta hasta el 10% de la fracción molar de Al y por encima del 20% de la fracción molar de Al no hay mucha diferencia en el campo eléctrico, lo que limita la corriente a un porcentaje de Al más alto.
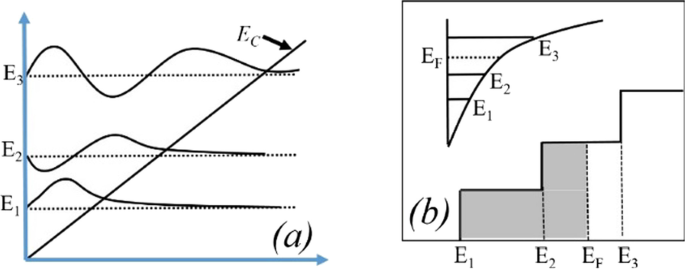
un Un potencial triangular que representa bien las subbandas de energía con Fang – Howard Airy función de onda. b Solo subbandas de energía más baja ( E 1 y E 2 , inferior al nivel de Fermi) están ocupados [28]
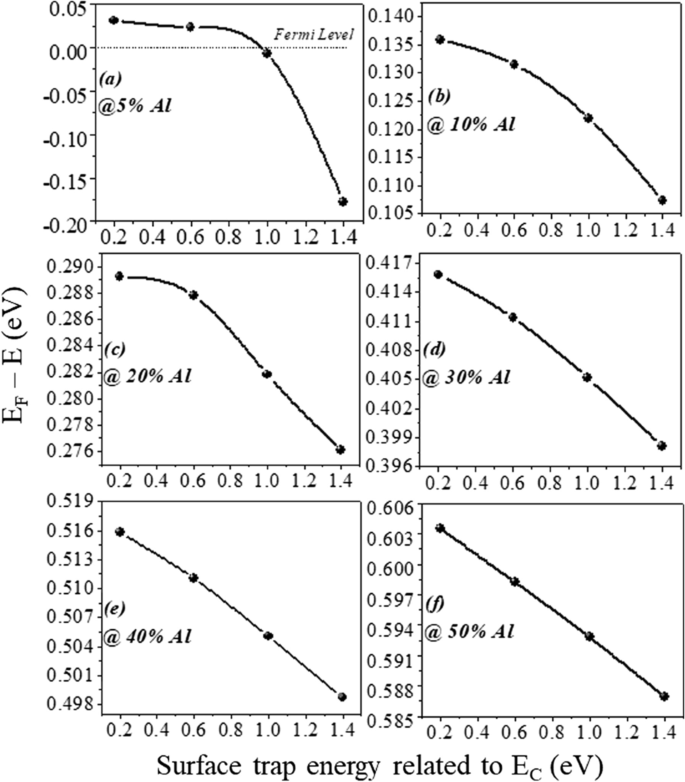
un - f ( E F - E ) variación con la energía del donante de superficie para toda la concentración de aluminio
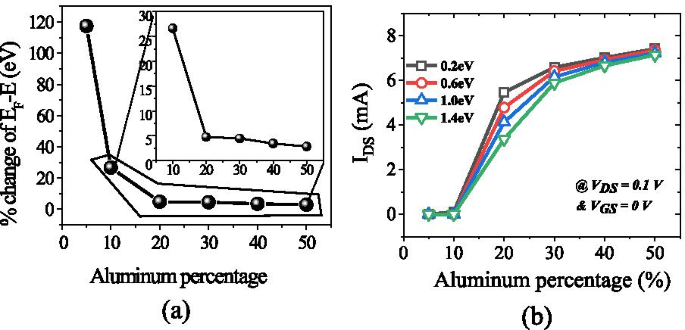
un El cambio porcentual de energía E con concentración de aluminio cuando la energía del donante superficial cambia de profunda a superficial. b Drene la corriente y V DS =0,1 V y V GS =0 V en diferentes capas de energía de las trampas de donantes de superficie. Hasta un 10% sin corriente significativa observada en el dispositivo

Gráfico de contorno de la densidad de corriente total absoluta para energía donante de superficie de 0,6 eV en V DS =0,1 V y V GS =0 V
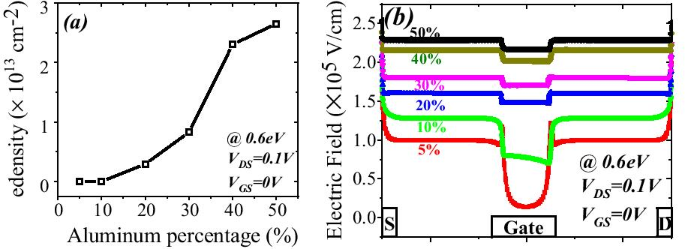
un Electron density variation with aluminum percentage and b electric field variation below gate and either side of gate for different aluminum percentage
Conclusion
In this paper, we comprehensively present the effect of surface donor traps along with aluminum percentage on electron density and quantum potential well. This manuscript demonstrated that the percentage change happens in 2DEG and notch below the Fermi level gets saturated above 20% of aluminum concentration when surface donor trap energy goes deep to shallow. The electron density in the two-dimensional quantum potential well is saturated approximately at 8%, whereas the energy below the Fermi level saturates somewhere around 2%. These two results are also in tune with each other, except 5% aluminum, having a condition for not forming two-dimensional well for relatively deep (> 0.9 eV) surface donors. Aluminum percentage above 10% forms two-dimensional quantum potential well even for deeper surface donor traps. The effect of surface donor traps on the surface potential also has been discussed in this work. The results of this paper may provide the impetus to the experimental result validation.
Disponibilidad de datos y materiales
All data are available on request.
Abreviaturas
- GaN:
-
Gallium nitride
- HEMT:
-
High-electron-mobility transistor
- 2DEG:
-
Two-dimensional electron gas
- DD:
-
Drift and diffusion transport model
- SRH:
-
Shockley–Read–Hall recombination model
Nanomateriales
- Evaluación de IoT y el impacto de 5G
- 5G y GaN:innovaciones futuras
- Ajuste de la química superficial de la polieteretercetona mediante revestimiento de oro y tratamiento con plasma
- Investigación sobre la polarización de la superficie de la heteroestructura de GaN / AlGaN / GaN con cubierta de Al2O3 mediante espectroscopia de fotoelectrones de rayos X de ángulo resuelto
- Ajuste de las morfologías de la superficie y las propiedades de las películas de ZnO mediante el diseño de la capa interfacial
- Electrohilado sobre sustratos aislantes controlando la mojabilidad y la humedad de la superficie
- Los efectos de acoplamiento de los polaritones de plasma superficial y las resonancias magnéticas dipolo en metamateriales
- Influencia de la rigidez elástica y la adherencia de la superficie en el rebote de nanopartículas
- Propiedades electrónicas de la adsorción de átomos de vanadio en una superficie limpia y cubierta de grafeno de Cu (111)
- Propiedades y propósitos:Aluminio Bronce
- Aprenda sobre los diferentes acabados superficiales de PCB y su impacto en su PCB



