Influencia de la rigidez elástica y la adherencia de la superficie en el rebote de nanopartículas

Resumen

Las colisiones granulares se caracterizan por un umbral de velocidad, que separa el régimen de baja velocidad de adherencia del grano del régimen de alta velocidad de rebote del grano:la velocidad de rebote, v _b . Este parámetro es particularmente importante para los nanogranos y tiene aplicaciones, por ejemplo, en astrofísica, donde entra en la descripción de la agregación de polvo por colisión. Las estimaciones analíticas se basan en la teoría macroscópica de Johnson-Kendall-Roberts (JKR), que predice la dependencia de v _b sobre el radio, la rigidez elástica y la adherencia superficial de los granos. Aquí, realizamos simulaciones atomísticas con potenciales de modelo que nos permiten probar estas dependencias para colisiones de nanogranos. Nuestros resultados no solo muestran que JKR describe cualitativamente bien la dependencia de los parámetros de los materiales, sino que también señalan considerables desviaciones cuantitativas. Estos son los más pronunciados para adherencias pequeñas, donde la rigidez elástica no influye en el valor de la velocidad de rebote.

Antecedentes

Podría decirse que el proceso más básico de la mecánica granular es la colisión de dos granos. A grandes velocidades de grano, los granos se vuelven a separar después de la colisión, y el resultado de la colisión puede caracterizarse por la mecánica clásica de las colisiones inelásticas. Sin embargo, a velocidades de grano pequeñas, los granos se pegarán. El límite entre las colisiones de pegar y rebotar [1] puede denominarse velocidad de rebote, v _b . Este parámetro es particularmente importante para los nanogranos y tiene aplicaciones, por ejemplo, en astrofísica, donde entra en la descripción de la agregación de polvo por colisión [2, 3].

Se ha utilizado la mecánica de contacto macroscópica para derivar una predicción para v _b . Se basa en la teoría de Johnson-Kendall-Roberts (JKR) [4], que describe la colisión de dos esferas adhesivas utilizando la rigidez elástica y la adherencia de la superficie como entrada física básica. Cuantitativamente, estas cantidades se describen mediante el módulo de indentación, E _ind = E / (1− ν ² ), donde E es el módulo de Young y ν el número de Poisson, y por la energía superficial γ . Con el radio de la esfera R y la densidad de masa ρ , la velocidad de rebote de dos esferas idénticas dice [1, 5, 6]

$$ {v_ {b}} =\ left (\ frac {C} {\ rho} \ right) ^ {1/2} \ left (\ frac {\ gamma ^ {5}} {E _ {\ text {ind }} ^ {2} R ^ {5}} \ derecha) ^ {1/6}. $$ (1)

El valor de la constante C depende en gran medida de los supuestos de disipación de energía durante la colisión y se ha discutido para asumir valores entre 0,3 y 60 [1, 7].

La validez de esta predicción se ha estudiado predominantemente con respecto a su dependencia del tamaño [1, 5-8]. Con la disminución del tamaño de grano, las fuerzas adhesivas se vuelven más importantes y la velocidad de rebote aumenta. De hecho, los experimentos con nanogranos (granos de Ag y NaCl) [9] encuentran v _b estar en el rango de 1 m / s para tamaños de grano de unos 10 nm, pero aumentar considerablemente para granos más pequeños. Las simulaciones atomísticas basadas en la dinámica molecular (MD) han confirmado la R predicha ^−5/6 dependencia de colisiones entre granos de sílice amorfa de tamaños R =15-25 nm [7].

Hasta ahora, la dependencia prevista de v _b en los parámetros de materiales E _ind y γ no ha sido probado en detalle. Esto no se hace fácilmente en el experimento, ya que los diferentes materiales suelen diferir en ambas cantidades. Sin embargo, usando MD, podemos construir materiales modelo, que tienen propiedades idénticas, pero difieren solo en un aspecto, ya sea E _ind o γ . En este artículo, elegimos un modelo para Cu [10] pero variamos generosamente los parámetros de los materiales hasta en un orden de magnitud de los valores reales. Dado que no encontramos ningún rebote para las nanopartículas amorfas en este sistema, nos centramos en los granos cristalinos (fcc).

Métodos / Experimental

Usamos el potencial Morse

$$ U (r) =D \ left [e ^ {- 2 \ alpha (r-r_ {0})} - 2 e ^ {- \ alpha (r-r_ {0})} \ right], $$ (2)

para describir la interacción entre dos átomos de distancia r . Los tres parámetros Morse D , α y r ₀ están determinados a describir la constante de celosía a , el módulo de volumen B y la energía cohesiva E _coh de un sólido de fcc a granel.

Para mayor precisión, fijamos la constante de celosía en a =3.615 Å (apropiado para Cu) en este estudio y también adoptar la masa atómica de Cu, para mantener la densidad de masa ρ en Eq. (1) fijo. El potencial se corta en r _c =2.5 a ; así, 12 capas vecinas, incluyendo un total de 248 átomos, interactúan con cada átomo. Se evalúan varios 100 potenciales para B en el rango de 403 a 1008 GPa, y E _coh en el rango de 0,35 a 3,54 eV. Tenga en cuenta que los módulos de volumen estudiados aquí son más grandes y las energías cohesivas son más pequeñas que los valores de Cu real ( B =134,4 GPa, E _coh =3.54 eV [11]), ya que para los valores reales, no observamos ningún rebote.

Determinamos el módulo de indentación E _ind para el esfuerzo uniaxial en la dirección (100) del módulo de Young y el número de Poisson en esta dirección ([12], p. 32). La Figura 1 a muestra la dependencia de E _ind en B . Vemos que estas cantidades obedecen a una relación lineal; a un módulo de volumen constante, una disminución de la energía cohesiva permite que E _ind aumentar.

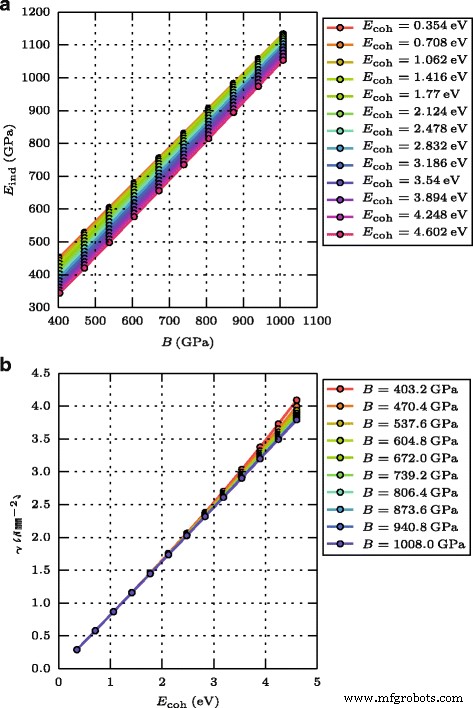
Parámetros de materiales. Dependencia de a el módulo de indentación E _ind en el módulo de volumen B y de b la energía superficial γ en la energía cohesiva E _coh

La energía superficial de (100) facetas se calcula a partir de la diferencia de energía de un cristal a granel y un cristal con una superficie abierta (100) dividiendo el área de la superficie abierta [13]. La figura 1 b muestra que γ es aproximadamente proporcional a E _coh; las desviaciones solo son visibles para rigideces más pequeñas y materiales fuertemente adheridos.

Construimos granos cortando una esfera con radio R =9 a =33 Å fuera de la red fcc, que contiene alrededor de 12.000 átomos. Por su construcción, tienen una superficie facetada. Están relajados para equilibrar sus superficies; ligera relajación de la superficie, pero no se observó reconstrucción de la superficie. Las colisiones se inician duplicando los granos y disparándolos entre sí con una velocidad relativa v . Solo se consideran las colisiones centrales, donde las dos facetas enfrentadas (100) chocan de frente, ver Fig. 2.

Configuración inicial de la colisión

Para determinar la velocidad de rebote, realizamos colisiones con varias velocidades. El algoritmo utilizado aquí se basa en un esquema de bisección simple. Verificamos que las colisiones con una velocidad de 250 m / s están rebotando para todos los sistemas de colisión estudiados aquí, mientras que a velocidad de fuga, las colisiones se mantienen. Luego, las simulaciones se ejecutan a la media aritmética de la velocidad de rebote más baja conocida y la velocidad de adherencia más alta conocida. Este procedimiento se repite hasta que la diferencia entre la velocidad de rebote más alta y la velocidad de rebote más baja sea inferior al 10% de su valor medio. v _b se toma como la media aritmética de la velocidad de adherencia más alta y la velocidad de rebote más baja; estos dos últimos valores también se toman para indicar el error de nuestro cálculo en las gráficas. Las simulaciones se realizaron utilizando el software de código abierto LAMMPS [14], y el código es esencialmente el mismo que el utilizado en nuestros estudios anteriores sobre colisiones de sílice [7] y partículas de hielo de agua [15].

Resultados

La figura 3 ofrece una descripción general de los resultados obtenidos.

$$ {v_ {b}} \ propto \ gamma ^ {0.588} E _ {\ text {ind}} ^ {- 0.155}. $$ (3)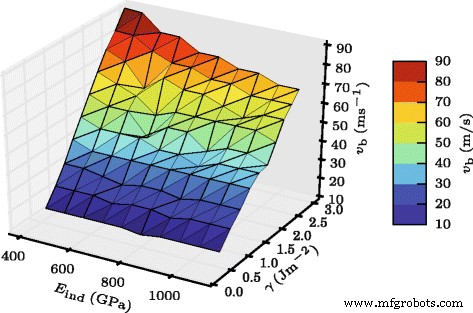

Velocidad de rebote. Gráfico tridimensional de la dependencia de la velocidad de rebote v _b en el módulo de indentación E _ind y la energía superficial γ

Así, las principales características de la ley JKR, Eq. (1):un aumento de v _b con adherencia y una disminución con rigidez elástica — se reproducen, pero las dependencias son más débiles que las del caso JKR.

La Figura 4 analiza con más detalle estas dependencias. Dado que determinamos las velocidades de rebote para materiales con B fijo o E _coh , los analizaremos para estos valores fijos, pero presentaremos las dependencias en términos de E _ind y γ para hacer conexión con la predicción de JKR, Eq. (1). Para una energía cohesiva constante E _coh , v _b depende como una ley de potencia de la rigidez elástica,

$$ v_ {b} \ propto E _ {\ text {ind}} ^ {- a}, $$ (4)

Velocidad de rebote. Dependencia de la velocidad de rebote v _b en el a módulo de indentación E _ind y la b energía superficial γ . Las líneas denotan ajustes de la ley de potencias. c muestra la dependencia del exponente de potencia, a , Eq. (4), sobre la energía cohesiva. La línea denota un ajuste lineal para guiar el ojo

donde a =0.28 (0.26, 0.02) para E _coh =3,54 (2,12; 0,35) eV. Por tanto, el exponente a =0.33 predicho por JKR está de hecho casi recuperado para altas energías superficiales; sin embargo, la dependencia se vuelve más suave al disminuir γ y desaparece por completo para superficies débilmente adhesivas. Tenga en cuenta que en el caso de que la energía de la superficie desaparezca, todas las colisiones deben rebotar; esto explica el papel desvanecido de la rigidez elástica en este caso.

La Figura 4 c muestra los exponentes de potencia de la dependencia de v _b ( E _ind ), Eq. (4), obtenido de nuestras simulaciones. La trama demuestra claramente el aumento de la dependencia de E _ind con energía cohesiva creciente y, por tanto, energía superficial, como lo indica la línea de ajuste lineal roja.

Para una rigidez elástica fija, B , la dependencia de v _b en γ muestra una imagen más simple, vea la Fig. 4 c. La ley de potencia encaja, v _b ∝ γ ^{- b} , da valores bastante consistentes de b =0,67 (0,59; 0,53) para B =403 (739, 1008) GPa, y por lo tanto muestran solo una leve dependencia de B y por lo tanto E _ind . Sin embargo, tenga en cuenta que estas dependencias son más suaves que el valor de b =0,83 predicho por la ecuación. (1). A medida que aumenta la rigidez, las desviaciones de la predicción JKR se vuelven más fuertes. De hecho, se sabe que JKR falla en sistemas demasiado rígidos [16, 17]. Para tales sistemas, se cree que la teoría de Derjaguin-Muller-Toporov (DMT) [18] se aplica mejor; sin embargo, no parece haber surgido ninguna predicción de la velocidad de rebote de esa teoría.

En general, las velocidades de rebote encontradas aquí están por debajo de 100 m / s. Enfatizamos que para valores realistas del potencial de Morse apropiados para Cu, encontramos que se pega en todo el rango de velocidades y no hay rebotes. Esto está en línea con simulaciones recientes de colisiones de esferas de Cu (7–22 nm de diámetro) con una superficie de Al realizadas por Pogorelko et al. [19, 20] que encuentran que se mantienen a velocidades de 1000 m / s. La razón por la que encontramos rebotes en nuestras simulaciones es que usamos potenciales de modelo en los que los módulos elásticos aumentan generosamente y la unión de la superficie disminuye, con respecto a los valores que caracterizan al Cu real.

Por encima del umbral de rebote, las colisiones se caracterizan por el coeficiente de restitución,

$$ e =| v '| / | v |, $$ (5)

que compara la velocidad relativa después de la colisión, v ^′ , a eso antes de la colisión, v , y por lo tanto mide la inelasticidad de la colisión. Para colisiones continuas, evidentemente, e =0. La teoría de JKR sugiere una ley [4–6]

$$ e _ {\ text {JKR}} =\ alpha \ sqrt {1- \ left (\ frac {v_ {b}} {v} \ right) ^ {2}}, $$ (6)

donde introdujimos el factor α tener en cuenta la disipación de energía [7].

La Figura 5 muestra dos casos de dependencia de la velocidad de e ; consideramos que estos son representativos de todo el rango de valores de rigidez y adherencia investigados. En todos estos casos, no hay una disipación importante de energía durante la colisión; α es de alrededor de 0,9. A energías de superficie suficientemente grandes, Fig.5 a, e sigue bastante bien la predicción de JKR, Eq. (6). En pequeño γ , sin embargo, en la Fig. 5 b, se ve una zona de transición más estrecha, en la que e cambia de 0 a casi 1; esta zona de transición no está bien descrita por la predicción de JKR, Eq. (6).

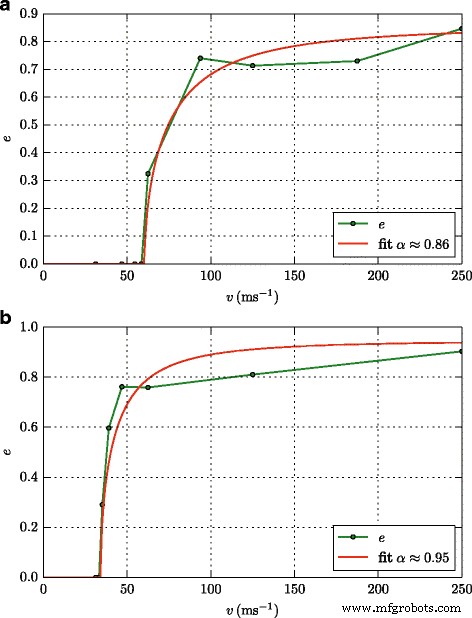
Coeficiente de restitución. Dependencia del coeficiente de restitución, e , en velocidad de colisión, v , para un fuerte ( γ =2,32 J / m ² ) ( a ) y débilmente ( γ =0,89 J / m ² ) ( b ) superficie adhesiva. El módulo de volumen es idéntico en ambos casos, B =940,8. Los símbolos denotan resultados de simulación, mientras que la curva se ajusta a la predicción JKR, Eq. (6), con α =0.86 ( a ) y 0,95 ( b )

Discusión

En el régimen de adherencia, el coeficiente de restitución se mantiene por debajo de 1, lo que indica pérdidas de energía inelásticas durante la colisión. Verificamos que las colisiones son puramente elásticas en el sentido de que no se generó plasticidad permanente durante la colisión; Se utilizó la herramienta de software OVITO [21] para comprobar la producción de dislocaciones. Para velocidades más altas, v > 100 m / s, y esferas compatibles, las dislocaciones se formaron transitoriamente pero desaparecieron nuevamente después de la colisión. Observamos que durante la colisión de nanoesferas cristalinas de tamaño similar que interactúan a través del potencial genérico de Lennard-Jones, se pudo detectar una amplia producción de dislocaciones [22, 23], mientras que se identificaron zonas de transformación de cizallamiento en la colisión de esferas de sílice amorfa [7], ambas Los sistemas de colisión presentan, por tanto, plasticidad. En nuestro caso, los altos módulos elásticos impiden el establecimiento de deformaciones plásticas; Las pérdidas de energía inelástica son causadas únicamente por la excitación de vibraciones en las esferas colisionadas. Se puede concluir que la existencia de colisiones con rebote está relacionada con la supresión de pérdidas inelásticas durante las colisiones y, por tanto, con la supresión de la deformación plástica.

El comportamiento de e para γ pequeño subraya nuestros hallazgos anteriores para v _b que se exhiben grandes desviaciones de JKR para sistemas débilmente adhesivos. Concluimos que para una adhesión débil, la velocidad de rebote y también el estado del sistema después del rebote dependen solo débilmente de otras características del sistema, como E _ind y v .

Conclusiones

La predicción de la teoría JKR de los contactos elásticos adhesivos se ha probado mediante simulaciones MD dedicadas de nanogranos utilizando potenciales de modelo. Encontramos que las tendencias generales de la dependencia de la velocidad de rebote se reproducen razonablemente bien por la teoría JKR cuando se varía la rigidez del material y la adhesión del material hasta en un orden de magnitud. Sin embargo, encontramos desviaciones sistemáticas para granos débilmente adhesivos; en este caso, el umbral de rebote se vuelve independiente de la rigidez del material, y el coeficiente de restitución casi no muestra dependencia de la velocidad por encima de v _b . También para una adhesión más fuerte, la dependencia de la velocidad de rebote de γ es sistemáticamente más pequeño que el predicho por JKR.

Estas desviaciones apuntan a una descripción incompleta de las colisiones de nanopartículas mediante la teoría del contacto macroscópico. El trabajo futuro intentará extender este estudio a granos cristalinos con otras orientaciones y con radios más grandes, y a granos amorfos.

Aptitud ecológica en la síntesis y estabilización de nanopartículas de cobre:actividades catalíticas, antibacterianas, citotóxicas y antioxidantes Estimación del almacenamiento de energía del supercondensador basada en ecuaciones diferenciales fraccionales

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias