Estimación del almacenamiento de energía del supercondensador basada en ecuaciones diferenciales fraccionales

Resumen

En este artículo, se presentan nuevos resultados sobre el uso solo de mediciones de voltaje en terminales de supercondensadores para estimar la energía acumulada. Para ello, se realiza un estudio basado en la aplicación de modelos de orden fraccionario de circuitos de carga / descarga de supercondensadores. A continuación, se utilizan estimaciones de parámetros de los modelos para evaluar la cantidad de energía acumulada en el supercondensador. Los resultados obtenidos se comparan con la energía determinada experimentalmente midiendo el voltaje y la corriente en terminales de supercondensadores. Todas las pruebas se repiten para varias formas y parámetros de señales de entrada. La consistencia muy alta entre los resultados estimados y experimentales confirma completamente la idoneidad del enfoque propuesto y, por lo tanto, la aplicabilidad del cálculo fraccional al modelado del almacenamiento de energía del supercondensador.

Antecedentes

A día de hoy, los supercondensadores son los componentes principales de muchos dispositivos y sistemas, por ejemplo, sistemas de recuperación de energía y electricidad de respaldo, así como aplicaciones automotrices, vehículos híbridos y muchos otros. La capacidad de acumular carga sin reacciones químicas hace que dichos elementos tengan un número cientos de veces mayor de ciclos de carga / descarga en comparación con las baterías típicas [1]. Además, las altas tasas de carga / descarga los hacen efectivos para aplicaciones en sistemas de recuperación de energía utilizados, por ejemplo, en el transporte o en fuentes de energía renovables [2, 3]. En todas estas aplicaciones, el parámetro clave es la información sobre la cantidad de energía acumulada en el supercondensador [4, 5]. Desafortunadamente, la conocida relación para los capacitores típicos que permite determinar la información, es decir (1/2) C U ² , no se puede utilizar [6]. La cantidad de energía acumulada no se puede determinar sobre la base del voltaje en los terminales del condensador únicamente. La principal razón de esto es el proceso de difusión asociado con la redistribución de carga [1, 7]. Es por esto que muchos investigadores han estado tratando de determinar un modelo de supercondensador que permitiera estimar el comportamiento de un sistema real. Actualmente, los investigadores adoptan principalmente las combinaciones de elementos electrónicos típicos, por ejemplo, RC cuadripolo o en serie y combinaciones paralelas de dichos elementos. Sin embargo, todos estos modelos asumen una relación entre la corriente del supercondensador y el voltaje en su terminal en forma de una ecuación diferencial típica de orden entero [3-5, 7].

Pero resulta que algunas posibilidades completamente nuevas para la estimación de energía en tales sistemas pueden obtenerse mediante la aplicación del cálculo fraccional [8, 9]. El cálculo diferencial de orden no entero se propuso hace más de 300 años, pero cuestiones importantes de implementación están relacionadas con el advenimiento de las computadoras y su uso en el modelado de sistemas dinámicos de tiempo discreto [10-14]. La aplicación del cálculo fraccional al problema de la estimación de parámetros de supercondensadores no es un tema nuevo. Hay muchas publicaciones en este campo [15-25]. Los autores realizan la tarea de estimar parámetros tanto en dominios de frecuencia como de tiempo [26].

Este artículo es una versión ampliada de la presentación de la conferencia del autor [27], en la que se ha introducido brevemente un enfoque de orden fraccionario para estimar la energía acumulada en el supercondensador.

La estimación precisa de los parámetros de los supercondensadores también es de suma importancia para evaluar su fiabilidad [28-31]. Los procesos de degradación permanente dentro del supercondensador pueden cambiar la resistencia y capacitancia en serie equivalente. Por lo tanto, la determinación precisa de estos parámetros, basada en el método propuesto, también permite evaluar con precisión el rendimiento del condensador.

Este artículo comienza con algunos preliminares relacionados con la integración y diferenciación de orden fraccionario. A continuación, presenta el método de estimación de parámetros utilizado durante las pruebas y propone un nuevo método de cálculo de energía basado en el cálculo fraccional. La sección de Resultados y Discusión presenta la energía calculada para varios escenarios y la compara con valores de referencia (medidos). Las conclusiones y contribuciones se resumen en la sección de Conclusiones.

Métodos

El uso de materiales porosos en supercondensadores y la forma específica de acumulación de carga hacen que los enfoques tradicionales basados en modelos derivados de orden entero no sean lo suficientemente precisos. Muchos investigadores han propuesto varias soluciones en forma de combinación de RC típicos elementos con valores constantes o variables [4, 7]. Pero resulta que definitivamente se puede obtener una mayor precisión utilizando el cálculo diferencial de orden no entero para definir las relaciones entre la corriente y el voltaje del supercondensador [17, 19]. Además, una solución de este tipo puede resultar en una estructura de modelo muy simple, al tiempo que proporciona una precisión muy alta [18].

Diferencia de orden fraccionario – Cálculo integral

El cálculo diferencial de orden fraccionario se conoce desde hace más de 300 años. Sin embargo, solo varios años recientes han traído su popularidad en el modelado de fenómenos y procesos físicos. Se cree que la descripción de la dinámica con una derivada o integral de orden no entero puede ser uno de los métodos más efectivos para modelar las propiedades reales de muchos fenómenos complejos y procesos industriales, especialmente basados en materiales y tecnologías novedosos [10, 12, 13 , 32–34].

El cálculo diferencial o integral de orden no entero es una generalización del cálculo clásico al orden α que pertenece al conjunto de números reales \ (\ mathcal {R} \). El operador diferencial-integral de orden \ (\ alpha \ in \ mathcal {R} \) de la función f ( t ) en el rango [ a , t ] se puede escribir de la siguiente manera

$$ {{} _ {a} \ mathcal {D} _ {\ textit t} ^ {\ alpha}} f (t) =\ left \ {{\ begin {array} {lcl} {\ frac {\ mathrm {d} ^ {\ alpha} \ textit {f (t)}} {\ mathrm {d} \ textit {t} ^ {\ alpha}}} &\ text {para} &\ alpha> 0 \\ f ( t) &\ text {para} &\ alpha =0 \\ \ int_ {a} ^ {t} f (\ tau) \ textrm {d} {\ tau ^ {\ alpha}} &\ textrm {para} &\ alpha <0, \\ \ end {matriz}} \ right. $$ (1)

asumiendo que la función f ( t ) es múltiples veces diferenciable e integrable. En cuanto al operador (1), existen muchas definiciones de su realización. Tales definiciones difieren en propiedades y áreas de aplicación. Las más populares son las definiciones de Riemann-Liouville, Caputo y Grünwald-Letnikov (GL) [34]. Este último se utilizará en este documento en la forma

$$ {} _ {a} \ mathcal {D} _ {t} ^ {\ alpha} f (t) ={\ lim} _ {h \ to 0} \ frac {1} {h ^ {\ alpha} } \ sum \ limits_ {j =0} ^ {\ left [{\ frac {t} {h}} \ right]} (- 1) ^ {j} {\ alpha \ elige j} f (t-jh) , $$ (2)

donde el binomio \ (\ alpha \ choose j \) se define de la siguiente manera

$$ {\ alpha \ elija j} =\ left \ {\ begin {array} {lll} 1 &\ textup {for} &j =0 \\ \ frac {\ alpha (\ alpha-1) \ dots (\ alpha -j + 1)} {j!} &\ text {for} &j> 0. \ end {matriz} \ right. $$ (3)

Para obtener un modelo fraccional en momentos discretos de tiempo, la definición de GL en una forma discreta se simplifica como

$$ \ Delta_ {h} ^ {\ alpha} f (t) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {t} (- 1) ^ {j } {\ alpha \ elija j} f (tj). $$ (4)

Hay varios esquemas de discretización para GL Eq. (4). Los más populares incluyen los operadores de diferencias hacia atrás (Euler), trapezoidales (Tustin) y Al Alaoui. Usando el método de Euler, la derivada fraccionaria en momentos de tiempo discretos k se puede presentar como

$$ \ Delta_ {h} ^ {\ alpha} f (k) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {k} (- 1) ^ {j } {\ alpha \ elija j} f (kj), \; k =0,1, \ ldots. $$ (5)

La suma infinita de muestras anteriores debe estar en sistemas reales limitada a un valor finito debido a la memoria limitada y al tiempo de cálculo limitado. Ahora, la aproximación de tiempo discreto truncado o de longitud finita de GL es

$$ \ Delta ^ {\ alpha} f (k) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {L} (- 1) ^ {j} {\ alpha \ elija j} f (kj), \; k =0,1, \ ldots, $$ (6)

donde f ( l ) =0 para l <0 y L es la longitud del modelo (6) [23]. La reducción del número de muestras da como resultado una disminución de la precisión del cálculo. Esto es importante para los sistemas que operan en un tiempo continuo. Algunos otros tipos de solución son algoritmos que aproximan diferen- cias integrales fraccionarias con modelos de orden entero. Un ejemplo pueden ser los filtros recursivos de Oustaloup [35]. Otro modelo de longitud finita eficaz es el FFLD, que es una combinación del modelo truncado (6) y una diferencia basada en Laguarre [24, 36, 37].

Todos los resultados de identificación, así como las mediciones de energía, se obtienen basándose en todas las muestras en la ventana de observación (larga) L , es decir, con la máxima precisión. La Figura 1 presenta las respuestas escalonadas de integración y diferenciación obtenidas con base en (6), para k =0,1,…, L y para varios valores de orden de integración / diferenciación α . Asumiendo diferentes valores de orden α , se pueden modelar con mayor precisión diferentes procesos físicos, especialmente los de difusión.

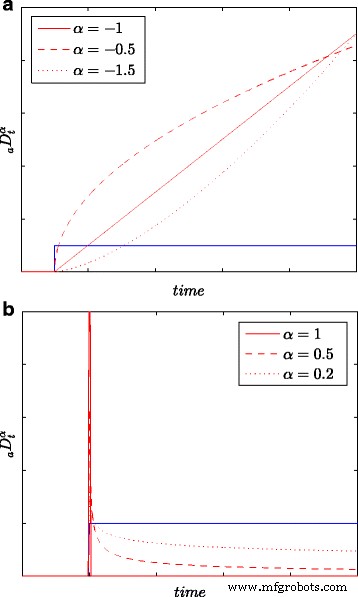
Respuestas a pasos para la integración ( a ) y diferenciando ( b ) modelos con varios órdenes α

Estimación de parámetros para modelo fraccional

Los resultados de todas las mediciones de energía y los procedimientos de identificación presentados en este documento se obtuvieron para un supercondensador cargado desde una fuente de voltaje controlado. En tal sistema, la corriente del supercondensador i _C ( t ) debe estar limitado por una resistencia R conectado en serie con el supercondensador C (Figura 2). La estimación de todos los parámetros del supercondensador se realiza en función de la respuesta cuadripolo u _C ( t ) al paso de voltaje u ( t ) en su entrada. Elegir el valor apropiado del orden derivado α permite dar cuenta de un modelo de supercondensador de los fenómenos físicos relacionados con los procesos de difusión asociados con la redistribución de carga durante los procesos de carga y descarga. La resistencia en paralelo r _P además permite modelar la corriente de fuga. Usando el cálculo diferencial fraccional para modelar supercondensadores, la estructura del modelo puede ser de baja complejidad. Para el supercondensador cargado desde la fuente de voltaje, un modelo consta de solo dos elementos, es decir, un RC simple cuadripolo (Fig. 2a). Para capacidades bajas, la resistencia de serie r _S es importante (Fig. 2b), mientras que la corriente de fuga I _L puede estar representado adicionalmente por la resistencia paralela r _P (Figura 2c). Usando el cálculo de orden fraccionario para modelar el supercondensador, la relación entre el voltaje en los terminales del condensador y su corriente se puede expresar de la siguiente manera

$$ i_ {C} (t) =C _ {\ alpha} \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (t)} {\ mathrm {d} t ^ {\ alpha}}, $$ (7)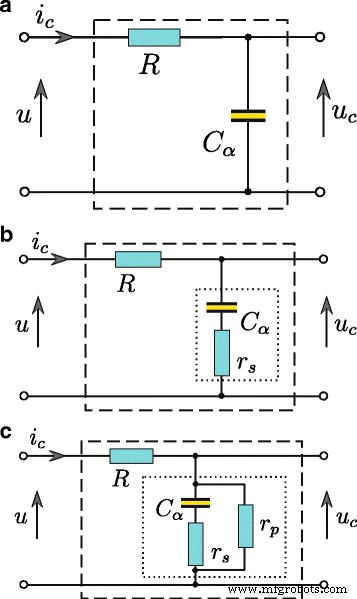

Supercondensador RC modelos, modelo base ( a ), expandido con una resistencia en serie ( b ), y con resistencia paralela adicional ( c )

donde el operador d ^α / d t ^α significa un operador de diferenciación de orden α y la unidad SI de C _α es [F / seg ^{1− α} ]. La configuración básica del supercondensador presentada en la Fig. 2a puede tratarse como un sistema inercial de primer orden y puede representarse mediante la función de transferencia fraccionada

$$ G (s ^ {\ alpha}) =\ frac {U_ {C} (s)} {U (s)} =\ frac {1} {Ts ^ {\ alpha} +1}, $$ (8 )

donde T = R C _α . Teniendo en cuenta la resistencia en serie r _S (Fig. 2b), el circuito se trata como un sistema de corrección de retardo de fase con la función de transferencia (comparar [24])

$$ G (s ^ {\ alpha}) =\ frac {1} {T_ {1} s ^ {\ alpha} +1} + \ frac {T_ {2} s ^ {\ alpha}} {T_ {1 } s ^ {\ alpha} +1}, $$ (9)

donde T ₁ = C _α ( R + r _S ) y T ₂ = r _S C _α . Además, teniendo en cuenta la resistencia en paralelo r _P que representa la corriente de fuga I _L (Fig. 2c), la función de transferencia del sistema se puede expresar como

$$ G (s ^ {\ alpha}) =\ frac {T_ {2} s ^ {\ alpha} +1} {T_ {1} s ^ {\ alpha} + K}, $$ (10)

donde K = R / r _P +1, T ₁ = C ( R r _s / r _P + R + r _S ) y T ₂ = r _S C . En el dominio del tiempo, Eq. (10) se puede presentar como

$$ \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (t)} {\ mathrm {d} t ^ {\ alpha}} =\ frac {1} {T_ {1}} (u (t) -Ku_ {C} (t)) + \ frac {T_ {2}} {T_ {1}} \ frac {\ mathrm {d} ^ {\ alpha} u (t)} {\ mathrm {d } t ^ {\ alpha}}. $$ (11)

El tiempo de respuesta del modelo definido por (11) se obtuvo transformándolo a la forma presentada gráficamente en la Fig.3, donde las operaciones de integración y diferenciación son de orden fraccionario α . Este modelo se utilizó durante el proceso de estimación de los parámetros del supercondensador. El supercondensador probado se identificó utilizando el sistema presentado en la Fig. 4a. El procedimiento de control de todo el sistema se desarrolló utilizando el software Matlab / Simulink con xPC Toolbox. El sistema constaba de una PC de escritorio (xPC Target) con la tarjeta de medida NI-DAQ instalada y una computadora maestra (xPC Host). Las computadoras estaban interconectadas a través de la red Ethernet. El supercondensador fue cargado y descargado por una fuente de voltaje (controlada por voltaje) (Fig. 4b) de eficiencia de corriente de hasta ± 3 A. El sistema de medición fue operado con la frecuencia de muestreo de 100 Hz, mientras que todas las mediciones y señales de control analógicas fueron procesado con resolución de 16 bits [25].

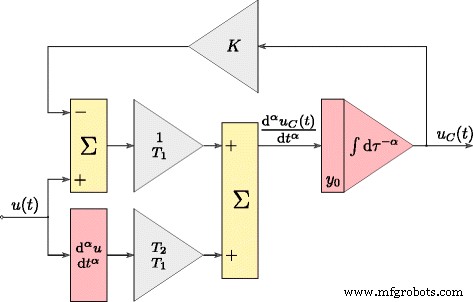
Estructura de Matlab del modelo de supercondensador en el dominio del tiempo

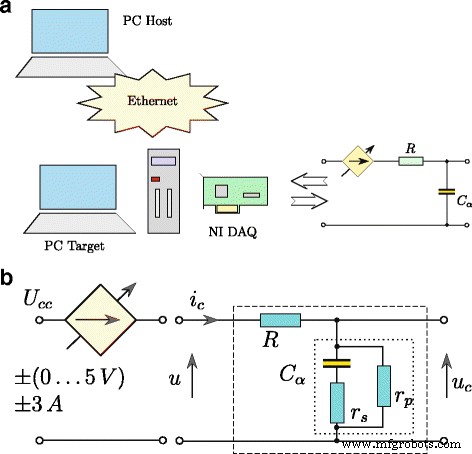
Estructura del sistema de medición ( a ) y esquema de carga / descarga de supercondensadores ( b )

El método principal para determinar las propiedades dinámicas de un sistema se basa en el análisis de la respuesta al escalón [38]. En relación al modelo del sistema, este método permite estimar sus parámetros. Para este estudio, se ha utilizado la señal de paso con varios voltajes (0.5 / 1.0 / 1.5 / 2.0 / 2.7 V) y duración constante (500 s) (ver Fig. 5 y Tabla 2). Por otro lado, una de las aplicaciones típicas de los supercondensadores es la acumulación o entrega de energía a los sistemas eléctricos. En este caso, la tasa de cambio de voltaje es bastante pequeña. Para simularlo se utilizó la señal de 400 mVpp y 0.03 rad / s con offset de 2 V (Fig. 6). Además, para examinar la influencia de los cambios de voltaje y frecuencia en los parámetros estimados, se utilizaron varios valores de estos últimos (ver Tabla 3).

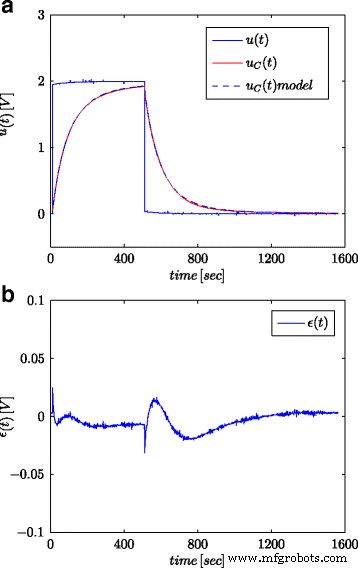
Respuestas escalonadas para el supercondensador probado y su modelo fraccional ( a ) y el error de respuesta del modelo ( b )

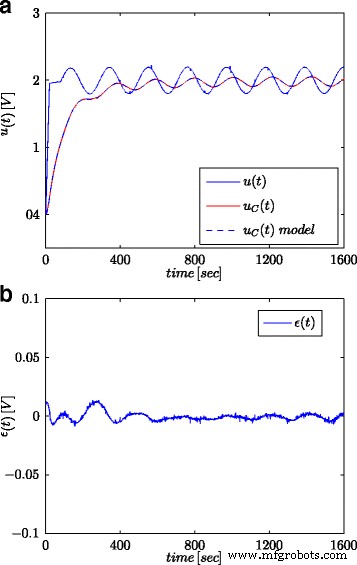
Respuestas de ondas sinusoidales para el supercondensador probado y su modelo fraccional ( a ) y el error de respuesta del modelo ( b )

Existen varios métodos para estimar los parámetros del modelo. El principal objetivo del procedimiento de identificación en el dominio del tiempo aplicado en este trabajo fue estimar el vector de parámetros desconocidos θ =[ α , C _α , r _S , r _P ] del modelo fraccional presentado por (11). Se utilizó el método de mínimos cuadrados para minimizar el error inicial. Un criterio de optimización implicó la minimización del error estándar \ (\ | \ epsilon (k) \ | _ {2} ^ {2} \), donde

$$ \ epsilon (k) =u_ {C} (k) - \ hat {u} _ {C} (k), $$ (12)

donde u _C ( k ) es el voltaje de salida medido del sistema probado en el momento k , mientras que \ (\ hat {u} _ {C} (k) \) es el voltaje de salida del modelo considerado para la señal de entrada u ( k ). El problema de identificación ahora se reduce a encontrar un vector de parámetros θ ∈ Θ _anuncio eso minimizaría el criterio del cuadrado J de tal manera que

$$ \ min _ {\ theta \ in \ Theta_ {ad}} \ left \ {J =\ sum_ {0} ^ {N} {\ epsilon (k) ^ {T} \ epsilon (k)} \ right \} , $$ (13)

donde Θ _anuncio denota el conjunto de valores de parámetros admisibles y N significa el tiempo de simulación. Hay muchos algoritmos de optimización que se pueden utilizar para resolver el problema (13). Los resultados presentados en este artículo se obtuvieron mediante la implementación del algoritmo genético en el entorno de Matlab.

Cálculo de energía

Un cambio en la energía almacenada en el supercondensador depende de la potencia suministrada al condensador por unidad de tiempo y se puede describir de la siguiente manera

$$ \ mathrm {d} E (t) =P (t) \ mathrm {d} t. $$ (14)

Al expresar la potencia suministrada al capacitor como un producto de la corriente y el voltaje en los terminales del capacitor, el cambio de energía en un momento dado t se puede expresar como

$$ \ mathrm {d} E (t) =u_ {C} (t) i_ {C} (t) \ mathrm {d} t. $$ (15)

La energía total durante el intervalo de tiempo [ t ₁ , t ₂ ] se puede obtener integrando los cambios de energía durante ese tiempo

$$ E_ {tot} =\ int_ {t_ {1}} ^ {t_ {2}} \ mathrm {d} E (t) =\ int_ {t_ {1}} ^ {t_ {2}} u_ {C } (t) i_ {C} (t) \ mathrm {d} t. $$ (16)

Contabilización de Eq. (7), el almacenamiento total de energía se puede determinar como

$$ E_ {tot} =C _ {\ alpha} \ int_ {t_ {1}} ^ {t_ {2}} u_ {C} (t) \ frac {\ mathrm {d} ^ {\ alpha} u_ {C } (t)} {\ mathrm {d} t ^ {\ alpha}} \ mathrm {d} t. $$ (17)

Suponiendo t ₁ =0 y \ (E_ {t_ {1}} =0 \), la energía total almacenada en el supercondensador durante el intervalo de tiempo [0, t ] es

$$ E (t) =C _ {\ alpha} \ int_ {0} ^ {t} u_ {C} (\ tau) \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (\ tau) } {\ mathrm {d} \ tau ^ {\ alpha}} \ mathrm {d} \ tau. $$ (18)

Tenga en cuenta que para α =1 Eq. (18) se puede reducir al clásico

$$ E (t) =\ frac {1} {2} Cu_ {C} (t) ^ {2}. $$ (19)

Resultados y discusión

Inicialmente, se realizó el procedimiento para estimar el vector de parámetros del modelo de supercondensador utilizando el cálculo fraccional. La estimación se realizó con base en el sistema presentado en la Fig. 2c, generando un paso de voltaje u onda sinusoidal en su entrada. Las respuestas del modelo se calcularon en base a (11). Los resultados obtenidos por los dos procedimientos de identificación son muy similares, especialmente en el caso de la capacitancia fraccionada C _α y el orden fraccionario α (ver Tabla 1). Algunas diferencias en las estimaciones de resistencia en serie r _S puede ser el resultado de su dependencia de la frecuencia. La señal de paso consta de muchos armónicos de alta frecuencia, mientras que la onda sinusoidal solo uno:los 0.03 rad / s. Los resultados presentados se obtuvieron para el supercondensador comercial Samwha Green – Cap EDLC (DB), clasificado como 2.7 V con capacitancia nominal de 100 F y 8 m Ω resistencia máxima en serie equivalente ( r _S ) a 1 kHz.

Las Figuras 5a y 6a muestran el voltaje del supercondensador medido y las respuestas del modelo calculado, para señales escalonadas y sinusoidales, respectivamente, mientras que las Figs. 5b y 6b muestran el error de respuesta del modelo.

Todos los resultados obtenidos muestran una alta consistencia entre las respuestas del modelo y las mediciones reales a pesar de que se propusieron modelos relativamente simples. Algunas discrepancias pueden deberse al hecho de que los parámetros del modelo deben estimarse en el sistema de supercondensador cargado y descargado utilizando la fuente de corriente [25]. Además, estimaciones muy altas de r _P puede sugerir que esta resistencia podría excluirse del modelo de supercondensador que se muestra en la Fig. 2c. Esas estimaciones muy altas y sus altas discrepancias para diferentes entradas indican que las señales de prueba utilizadas para estimar este parámetro no son adecuadas. El modelo (10) se utilizó como forma más general. Sin embargo, para determinar con precisión todos sus parámetros, fue necesario utilizar otros procedimientos y señales de prueba. El valor de r _P caracteriza la corriente de fuga I _L y debe determinarse utilizando la señal de voltaje constante, pero durante un tiempo muy largo, del orden de varias docenas de horas.

Aunque el objetivo principal del estudio era medir la energía, varias condiciones de excitación afectaron en gran medida a todas las estimaciones de los parámetros (ver Tabla 2). Por ejemplo, el aumento de la amplitud del paso de voltaje cambió significativamente el orden de integración fraccional, como resultado del efecto creciente de los fenómenos de difusión dentro del supercondensador. También se puede ver en la Tabla 2 que el supercondensador es bastante no lineal. Como resultado de los cambios en el orden de integración, también se observa la variación de la capacidad fraccional. Esto también se aplica a la excitación sinusoidal. Los valores de los parámetros estimados, especialmente α y C _α —Depende de la amplitud y frecuencia (ver Tabla 3). Para frecuencias bajas, el valor de amplitud es importante, mientras que para frecuencias más altas el supercondensador se comporta como si estuviera excitado con un voltaje constante.

Cálculo de energía

Las Figuras 7a y 8a muestran valores medidos del voltaje y la corriente del supercondensador para la configuración que se presenta en la Figura 4b. Estos valores se utilizaron para calcular la energía total almacenada en el condensador (marcado como E ₁ en las Figs. 7b y 8b) según (16). Al igual que para los procesos de identificación de parámetros, los cálculos se realizaron tanto para el paso de voltaje como para la onda sinusoidal en la entrada del sistema. La energía calculada de tal manera para cada tiempo t se comparó con la energía calculada en función del voltaje y la capacidad de acuerdo con (19) (marcado como E ₃ en las Figs. 7b y 8b) y la energía calculada con cálculo de orden fraccionario (marcada como E ₂ en las Figs. 7b y 8b) según (18). Para Eq. (19), se adoptó un valor nominal de supercondensador ( C _n ), mientras que en (18) se utilizó el valor obtenido del proceso de estimación presentado en la Tabla 1. La Figura 7b muestra los resultados de las mediciones y los cálculos de energía para el paso de voltaje, mientras que la Figura 8b muestra estas mismas cantidades para la onda sinusoidal. Se realizaron cálculos similares para diferentes pasos de voltaje y excitaciones sinusoidales. La Figura 9a, b muestra un ejemplo de energías medidas y calculadas para dos pasos de voltaje de 0.5 V y 2.7 V, respectivamente. La Figura 10 muestra los cambios de energía para una señal sinusoidal con la frecuencia de 0.03 rad / seg y diferentes amplitudes de 0.1 / 0.25 / 0.5 y 0.7 V. Se puede observar que las diferencias en los valores de energía determinados corresponden a diferencias en los valores estimados. del orden fraccionario α . Cuanto mayor es la diferencia del valor - 1, mayor es la diferencia en las energías calculadas.

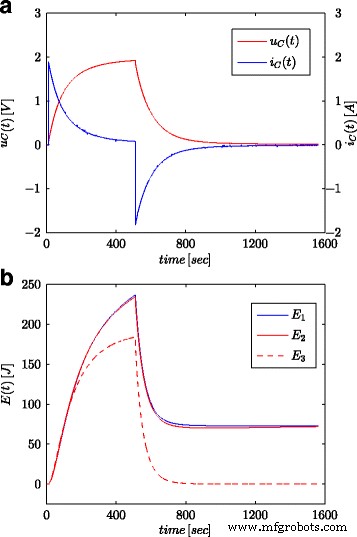
Respuestas escalonadas para voltaje y corriente del supercondensador ( a ) y valores de energía calculados ( b )

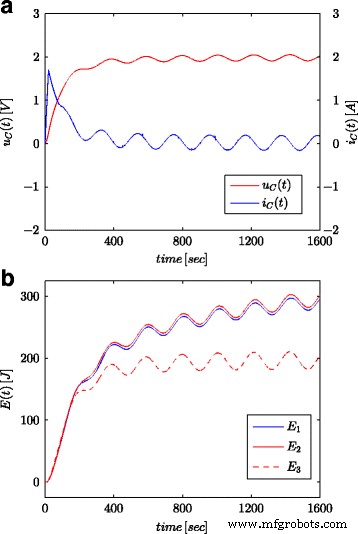
Respuestas sinusoidales para voltaje y corriente del supercondensador ( a ) y valores de energía calculados ( b )

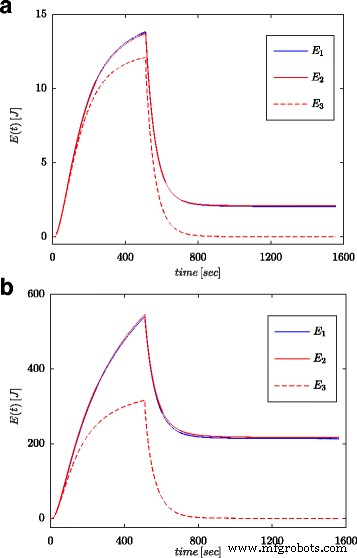
Cantidades de energía calculadas para excitaciones escalonadas de 0,5 V ( a ) y 2,7 V ( b )

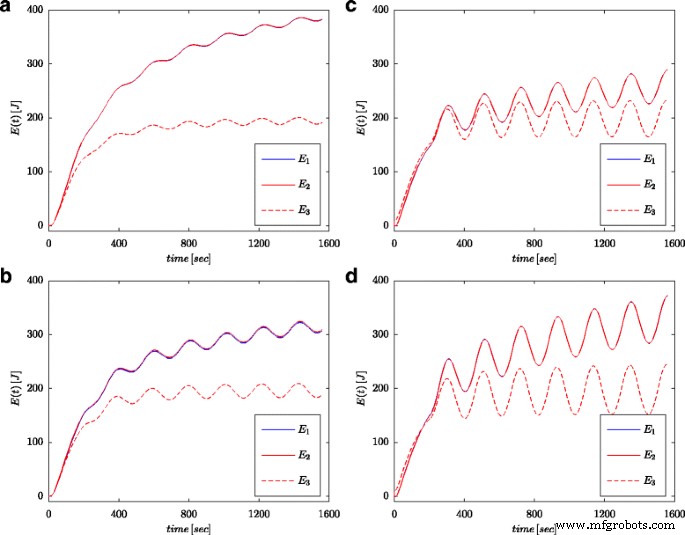
Cantidades de energía calculadas para excitaciones sinusoidales con frecuencia 0.03 rad / sy amplitudes 0.1 V ( a ), 0,25 V ( b ), 0,5 V ( c ) y 0,7 V ( d )

Discusión

El uso de electrodos de material poroso en supercondensadores en forma de carbón activo aislado por un separador muy delgado y el uso de mecanismos de acumulación de carga como la denominada doble capa, da un enorme aumento en su capacidad. Sin embargo, la aplicación de nuevos materiales y nuevas soluciones de diseño dan como resultado el hecho de que los cálculos matemáticos tradicionales en forma de derivadas e integrales de orden entero parecen inexactos. Las mediciones y los cálculos realizados demuestran la naturaleza de orden fraccionario de los supercondensadores. Mediante la estimación correcta del orden no entero α de derivada / integral, se pueden modelar con precisión los fenómenos y procesos que ocurren dentro del supercondensador utilizando modelos matemáticos simples.

Teniendo en cuenta el valor real de la energía acumulada determinado por (16), el modelo de orden entero con parámetros nominales (19) subestima la cantidad de energía, mientras que el modelo fraccional (18) indica casi el mismo valor.

Las pruebas y mediciones realizadas se relacionaron con la carga y descarga del supercondensador mediante una fuente de voltaje. En condiciones industriales, los supercondensadores generalmente se cargan y descargan mediante fuentes de corriente. Esto puede cambiar la naturaleza del sistema porque el capacitor ya no es un sistema inercial, sino que se convierte en uno integrador típico. Sin embargo, las mediciones realizadas por el autor también indican la ocurrencia de procesos de difusión en tales casos. De todos modos, aquí se confirma la utilidad de la derivada / integral de Gründwald-Letnikov. Otro problema está relacionado con la implementación del operador GL diffo-integral como, por ejemplo, la diferencia GL finita o truncada (6), que puede ser computacionalmente oneroso. En investigaciones futuras, compararemos los aproximadores Oustaloup [35] y FFLD [24, 36, 37] para resolver eficazmente el problema de implementación.

La cantidad de almacenamiento de energía en el supercondensador calculada solo sobre el valor medido de la tensión terminal del supercondensador y utilizando el modelo (19) no es apropiada. El modelo (19) solo es válido si la corriente del capacitor se caracteriza por la derivada de orden entero de la tensión del capacitor ( i _C ( t ) =d u _C ( t ) / d t ). Esto no es cierto para el supercondensador como consecuencia de su construcción y materiales especiales usados. Sin embargo, el mismo problema ocurre con supercondensadores muy grandes cargados por fuente de corriente. También hay elementos bastante nuevos como superbaterías. En todas estas aplicaciones, los cambios de corriente no se caracterizan por la derivada de orden entero del voltaje terminal como consecuencia de las propiedades específicas de estos elementos.

Conclusiones

En este artículo, se ha presentado un nuevo enfoque para la estimación de la cantidad de energía acumulada en supercondensadores. El análisis se ha realizado aprovechando ciertas propiedades únicas de los modelos de orden fraccionario. Se ha demostrado que la aplicación de modelos tan sofisticados conduce a resultados muy precisos, que pueden obtenerse aunque los modelos en sí mismos no sean de alta complejidad. Esto se debe a la capacidad natural de la dinámica de orden no entero para modelar procesos de difusión, al igual que la redistribución de carga en supercondensadores. Los resultados de este documento han confirmado la naturaleza fraccional de los supercondensadores.

Influencia de la rigidez elástica y la adherencia de la superficie en el rebote de nanopartículas Evaluación de estructuras de grafeno / WO3 y grafeno / ceO x como electrodos para aplicaciones de supercondensadores

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias