Absorbedor perfecto de banda ultra estrecha y su aplicación como sensor plasmónico en la región visible
Resumen
Proponemos e investigamos numéricamente un absorbente de banda ultra estrecha perfecto con un ancho de banda de absorción de solo 1,82 nm y una eficiencia de absorción superior al 95% en la región visible. Demostramos que la absorción de banda ultra-estrecha perfecta se atribuye al efecto de acoplamiento inducido por resonancia de plasmón de superficie localizada. También se investiga la influencia de las dimensiones estructurales en el rendimiento óptico, y la estructura óptima se obtiene con la reflectividad extremadamente baja (0,001) de la caída de resonancia. El absorbedor perfecto puede funcionar como un sensor de índice de refracción con una sensibilidad de alrededor de 425 nm / RIU y la figura de mérito (FOM) llegando a 233,5, lo que mejora en gran medida la precisión de los sensores plasmónicos en la región visible. Además, la cifra de mérito correspondiente (FOM *) para este sensor también se calcula para describir el rendimiento de la detección de cambio de intensidad a una frecuencia fija, que puede ser de hasta 1,4 × 10 5 . Debido al alto rendimiento de detección, la estructura del metamaterial tiene un gran potencial en la unión biológica, fotodetectores integrados, aplicaciones químicas, etc.
Antecedentes
En los últimos años, los metamateriales plasmónicos basados en la resonancia de plasmón de superficie localizada (LSPR) han obtenido avances significativos debido a sus propiedades electromagnéticas y aplicaciones prometedoras como los resonadores monopolo [1,2,3,4,5,6,7,8] , la mejora de la transmisión de luz [9,10,11,12,13] y los sensores plasmónicos [14,15,16,17,18,19,20,21]. Para un absorbente de metamaterial, es ventajoso mejorar la absorción de ondas electromagnéticas, mientras que las pérdidas ópticas intrínsecas de los metales deben considerarse cuidadosamente en el diseño de otros dispositivos. El primer absorbente de metamaterial perfecto es propuesto y demostrado por Landy [22]. A partir de entonces, se han desarrollado rápidamente absorbentes de metamateriales perfectos [23,24,25,26,27,28,29,30,31], que pueden clasificarse generalmente como absorbentes de banda estrecha y absorbentes de banda ancha según sus diferentes requisitos de aplicación. Generalmente, los absorbentes de banda ancha se pueden usar en la recolección de energía, mientras que los absorbentes de banda estrecha se usan en sensores y fotodetectores monocromáticos.
En aplicaciones de detección, el sensor de índice de refracción plasmónico basado en absorbentes de banda estrecha ha atraído mucha atención. Hasta la fecha, se han informado muchos tipos diferentes de sensores de índice de refracción plasmónica que funcionan en la región de infrarrojos y terahercios, incluidas microcavidades híbridas [32, 33], nanodiscos [34], metasuperficie de tipo red [24], rejilla metálica [28] y así sucesivamente [35,36,37]. Tenga en cuenta que, en comparación con los sensores plasmónicos que funcionan en la región de infrarrojos, terahercios y microondas, los sensores que operan en la banda visible pueden realizar una periodicidad más pequeña de la estructura del metamaterial, lo que puede mejorar la utilización de estos dispositivos en muchas aplicaciones prácticas, como la química y biología [38]. Desafortunadamente, los sensores de índice de refracción plasmónica publicados anteriormente en la región visible generalmente tienen un FOM comparativamente bajo, lo que obstaculizará en gran medida su desarrollo y aplicación posteriores. En estudios teóricos, en 2015, Zhou et al. propuso teóricamente un sensor de índice de refracción en la región visible utilizando las estructuras de rejilla metálica de sublongitud de onda con una S de 300 nm / RIU, pero el FOM es sólo 2 [28]. Liu y col. diseñó un sensor multiespectral con nanocavidades plasmónicas de sublongitud de onda profunda y demostró una FOM de 58 [34]. Con los esfuerzos realizados por Liu et al., Se obtuvo un sensor de índice de refracción con el FWHM mínimo que alcanza los 3 nm y un FOM de 68,57 a través de la estructura plasmónica con metasuperficie tipo red [24]. En estudios experimentales, en 2014, Emiko y Tetsu demostraron experimentalmente un sensor LSPR basado en una estructura de nanoestrella de Au única con una S de 665 nm / RIU y una FWHM de hasta 40 nm [39]. Cho y col. informó una demostración experimental de un sensor de índice de refracción plasmónico con el S alcanzando 378 nm / RIU [40]. Tanto en teoría como en experimentos, muchos investigadores han hecho grandes esfuerzos para mejorar la FOM del sensor de índice de refracción que opera en la región visible. Sin embargo, sigue siendo un gran desafío diseñar un sensor de índice de refracción plasmónico con un FOM alto en la región visible, lo que limita severamente sus aplicaciones.
Para los sensores, es muy significativo aumentar la FOM. Por ejemplo, en el campo biológico, un sensor de índice de refracción de FOM más alto significa un rendimiento más fuerte en la detección de moléculas. La FOM del sensor en este trabajo puede llegar a 233,5, que es mucho más alta que la del sensor de índice de refracción plasmónico publicado en la región visible [24, 28, 34]. El sensor plasmónico se basa en la estructura periódica metal-dieléctrico-metal (MDM). Entonces, la estructura también puede operar como un absorbente plasmónico de banda ultra-estrecha perfecto con una eficiencia de absorción superior al 95% y una FWHM de solo 1,82 nm en la región visible. También investigamos las influencias de las dimensiones de la estructura y los parámetros del material en las propiedades ópticas del metamaterial. Además, demostramos que, en comparación con las estructuras MDM comunes, el uso de nanocintas triangulares en la estructura es útil para mejorar el rendimiento de absorción. Y mientras tanto, los mecanismos de absorción también se investigan y analizan en detalle. Teniendo en cuenta la fabricación de la estructura propuesta, las nanocintas triangulares pueden fabricarse mediante muchos métodos, como la litografía por haz de electrones [41], el moldeado [42] y la litografía de impresión [43]. Se espera que nuestro trabajo sea una guía para el diseño de un sensor plasmónico.
Métodos
La Figura 1 ilustra la sección transversal de una celda unitaria para la estructura de metamaterial propuesta. La estructura consta de dos matrices de nanocintas de oro sobre una fina capa de oro intercalada entre la capa dieléctrica y el sustrato, y hay una nanocinta de oro triangular entre las nanocintas de oro. En nuestra simulación, la permitividad del oro se caracteriza por el modelo Drude. El dieléctrico de la capa intermedia y el sustrato se establecen como NaF ( n =1.3) y MgF 2 ( n =1,4), respectivamente. Utilizamos el método bidimensional en el dominio del tiempo de diferencia finita (FDTD) para calcular la transmisión y la reflexión de la estructura propuesta y la absorción de toda la estructura se define como A =1 - R - T. Establecemos condiciones de límite de período en la dirección x, y la onda magnética transversal (TM) incide normalmente sobre la estructura con polarización a lo largo de la dirección x.
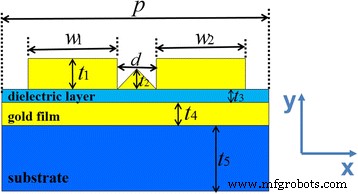
Esquema de la estructura de metamaterial propuesta de una celda unitaria
Como todos sabemos, el modelo de circuito LC equivalente se usa ampliamente para predecir cualitativamente la resonancia magnética excitada por LSPR para un absorbedor perfecto [44,45,46]. Para la conveniencia de la discusión sobre el modelo LC, el esquema de la estructura del absorbente de metamaterial se muestra en la Fig. 2a. Y el modelo LC equivalente se muestra en la Fig. 2b. Aquí, la capacitancia de la brecha entre las nanocintas en la unidad vecina se puede expresar como C g = ε 0 t 1 / ( P - d - 2 w ), donde ε 0 es la permitividad dieléctrica del entorno circundante. La capacitancia C m = c 1 ε 3 ε 0 (2 w + d ) / t 3 se utiliza para representar la capacitancia entre las nanocintas y la película de oro, donde c 1 es un coeficiente debido a la distribución de carga no uniforme en la superficie del metal y ε 3 es la permitividad de la capa dieléctrica [44,45,46]. La inductancia mutua de las nanocintas de oro y la película de oro viene dada por L m =0,5 μ 0 (2 w + d ) t 3 , donde μ 0 es la permeabilidad del entorno circundante. Para explicar la contribución de las cargas a la deriva en las nanocintas de oro y la película de oro, la inductancia cinética está dada por \ ({L} _e =\ left (2 w + d \ right) / \ left (\ gamma {\ varepsilon} _0 {t} _1 {\ omega} _p ^ 2 \ right) \), donde γ es un coeficiente que representa el área transversal efectiva de las nanocintas de oro y ω p es la frecuencia plasmática del oro [44,45,46]. Entonces, la impedancia total para el modelo de circuito LC equivalente se puede expresar como
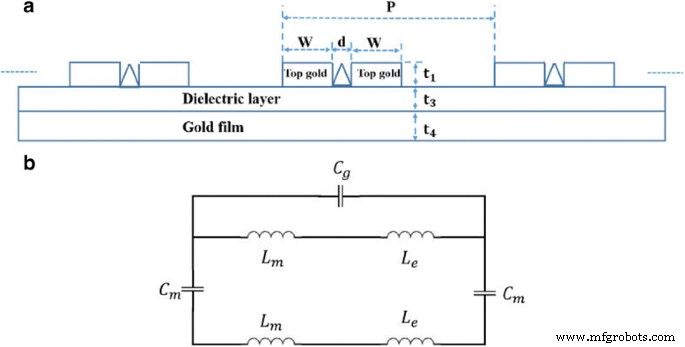
un Esquema de la estructura del absorbente de metamaterial. b Esquema del modelo de circuito LC equivalente para la estructura de la Fig. 6a
$$ {Z} _ {\ mathrm {t} ot} =\ frac {i \ omega \ left ({L} _m + {L} _e \ right)} {1 - {\ omega} ^ 2 {C} _g \ izquierda ({L} _m + {L} _e \ right)} - \ frac {2 i} {\ omega {C} _m} + i \ omega \ left ({L} _m + {L} _e \ right) $$ ( 1)La longitud de onda de resonancia se puede obtener cuando Z t ot =0.
$$ {\ lambda} _r =2 \ pi {c} _0 {\ left (\ frac {C_m {C} _g \ left ({L} _m + {L} _e \ right)} {C_m + {C} _g- \ sqrt {C_m ^ 2 + {C} _g ^ 2}} \ right)} ^ {\ frac {1} {2}} $$ (2)El acoplamiento entre las nanocintas en la unidad vecina es muy débil debido a la gran brecha ( P - d - 2 w ) entre las nanocintas. La influencia de C g se puede ignorar cuando C g es menos del 5% de C m . Por lo tanto, en esta situación, la longitud de onda de resonancia se puede simplificar a
$$ {\ lambda} _r \ approx 2 \ pi {c} _0 \ sqrt {\ left ({L} _m + {L} _e \ right) {C} _m} $$ (3)donde L m =0,5 μ 0 (2 w + d ) t 3 , \ ({L} _e =\ left (2 w + d \ right) / \ left (\ gamma {\ varepsilon} _0 {t} _1 {\ omega} _p ^ 2 \ right) \) y C m = c 1 ε 3 ε 0 (2 w + d ) / t 3 . En el modelo de circuito LC, las influencias de las dimensiones estructurales en la longitud de onda de resonancia se pueden predecir cualitativamente mediante la Ec. (3). Es fácil observar que la longitud de onda de resonancia λ r aumentaría con una permitividad mayor ( ε 3 ) de la capa dieléctrica, debido al aumento de C m . Del mismo modo, el ancho mayor w causará valores más grandes para L m , L e y C m , lo que da como resultado un desplazamiento hacia el rojo de la longitud de onda de resonancia. El aumento de permitividad ( ε 0 ) del entorno circundante dará como resultado una L más grande m C m valores, mientras que el otro término L e C m es independiente de ε 0 en Eq. (3). Por lo tanto, la longitud de onda de resonancia aumentará con el aumento de ε 0 .
Resultados y discusión
Luego, comenzamos la discusión con las siguientes dimensiones de estructura. La estructura tiene un período de celosía de P =580 nm en la dirección x. Las alturas de la nanocinta de oro cuadrada y la nanocinta de oro triangular se establecen respectivamente como t 1 =45 nm y t 2 =30 nm . Los espesores de la capa dieléctrica, la película de oro y el sustrato son t 3 =10 millas náuticas, t 4 =25 nm y t 5 =165 nm , respectivamente. El ancho de la nanocinta de oro triangular y la nanocinta de oro cuadrada son d =75 nm y w 1 = w 2 = w =142 nm , respectivamente. La Figura 3a presenta los espectros de absorción, reflexión y transmisión simulados de la estructura diseñada. Como se muestra en la Fig. 3a, la eficiencia de absorción puede alcanzar hasta el 95%, y la caída de reflectividad de la estructura por debajo de 0,001 se encuentra a 751,225 nm. El FWHM es 1,82 nm, que es mucho más estrecho que el del absorbente de banda estrecha informado anteriormente en la región visible [24, 28, 34, 39].
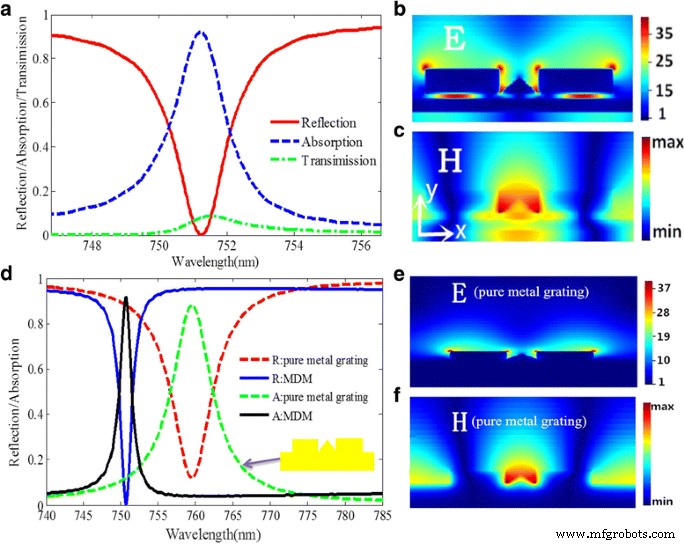
un Espectros de absorción, reflexión y transmisión de la estructura propuesta. b Distribuciones del campo eléctrico E de la estructura MDM en el pico resonante. c Distribuciones del campo magnético H de la estructura MDM en el pico resonante. d Los espectros de reflexión y absorción de la estructura de MDM y la estructura de rejilla de metal puro. e Distribuciones del campo eléctrico E de la estructura de rejilla de metal puro en el pico resonante. f Distribuciones del campo magnético H de la estructura de rejilla de metal puro en el pico resonante
Para elaborar el mecanismo físico del pico de absorción, las distribuciones del campo eléctrico E y el campo magnético H en el pico resonante se calculan y se representan en la Fig. 3b, c. Claramente, como se muestra en la Fig. 3b, la amplitud del campo eléctrico en los huecos puede alcanzar un valor tan alto como 35 veces mayor que la luz incidente. Por lo tanto, la estructura propuesta puede realizar no solo la absorción perfecta, sino también la mejora del campo eléctrico en una nano-iluminación, que es un fenómeno importante en las aplicaciones de biodetección. Como se muestra en la Fig. 3c, el campo más magnético se concentra en el espacio entre dos nanocintas de oro y algo penetra en la capa dieléctrica, lo que indica el efecto de acoplamiento resultante del LSPR. Luego, para comprender mejor la influencia de la capa dieléctrica y la película de oro en el FWHM ultra estrecho y el alto rendimiento de absorción, se analiza el espectro de absorción y reflexión y se compara entre la estructura de MDM y la estructura de rejilla de metal puro con el mismo parámetros dimensionales, como se muestra en la Fig. 3d. Obviamente, la estructura MDM tiene un FWHM más estrecho y una reflectividad más baja de la caída de resonancia. El campo eléctrico y el campo magnético de la estructura de rejilla metálica se simulan y se presentan en la Fig. 3e, f, respectivamente. Obviamente, en comparación con la distribución del campo magnético de la estructura MDM, el campo magnético de la estructura de rejilla metálica solo se encuentra en la superficie de la nanocinta de oro triangular sin que el campo magnético pase a través del metal, lo que se puede utilizar para explicar el resultado comparativo de la absorción entre la estructura de MDM y la estructura de rejilla metálica. Además, debido al comportamiento de acoplamiento en la estructura, como se muestra en la Fig.3b, la intensidad del campo eléctrico entre dos nanocintas de oro y la fina película de oro es aproximadamente 40 veces mayor que la de las ondas incidentes, que es mucho mayor que la reportada. en ref. [25].
La Figura 4a muestra el efecto de la configuración de polarización de la luz incidente sobre el espectro de absorción del absorbente de metamaterial propuesto. Puede verse que la estructura tiene un pico de absorción agudo en la configuración TM, pero no en la configuración TE. Obviamente, el LSPR no puede ser excitado por la luz incidente con configuración TE, lo que puede explicarse bien por la estructura asimétrica del absorbedor. Además, en un sistema real, debido a la dispersión de la superficie y los efectos del límite de grano en la fina película de oro, es probable que la constante de amortiguación de la fina película de oro sea más alta que la del oro a granel. Para tener en cuenta la influencia de la constante de amortiguación de la fina película de oro, la Fig. 4b muestra que el espectro de absorción calculado de las constantes de amortiguación de la película de oro es tres y cinco veces mayor que el del oro a granel. Evidentemente, se observan picos de absorción con diferentes amplitudes y FWHM. Los resultados muestran que el aumento de la pérdida de material de metal es desfavorable para mejorar aún más las propiedades de absorción del absorbente de banda estrecha propuesto, que son consistentes con la investigación anterior [17].
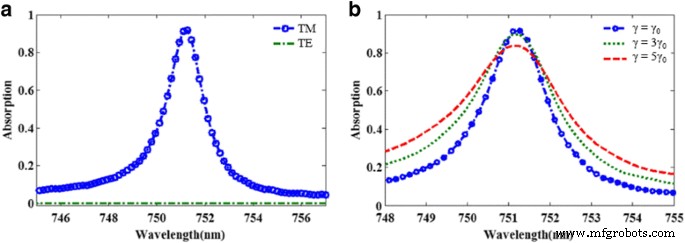
un Los espectros de absorción de la estructura propuesta bajo configuraciones de polarización TE y TM. b Espectros de absorción calculados en función de la constante de amortiguación de la película de oro
En general, se sabe que las propiedades del absorbente de metamaterial están fuertemente influenciadas por la forma geométrica y las dimensiones estructurales de la estructura. En primer lugar, investigamos el efecto de la nanocinta de oro triangular en el espectro de reflectancia de la estructura diseñada. La nanocinta de oro triangular de la estructura se elimina o se transforma en una nanocinta de oro cuadrada y semielipse, respectivamente, como se muestra en la Fig. 5c-e, y los otros parámetros se mantienen sin cambios en la simulación. Los espectros de reflexión de estas tres estructuras se analizan y comparan con el de la estructura original como se muestra en la Fig. 5f – h, respectivamente. Es fácil observar que la estructura original puede lograr un FWHM más estrecho y una caída de reflectividad menor que otras tres estructuras. Para comprender mejor estos resultados, como se muestra en la Fig. 5i – 1, la distribución del campo magnético (H) en el pico resonante de estas cuatro estructuras se traza respectivamente y el color presenta la intensidad del campo magnético. La intensidad del campo magnético de la estructura original es obviamente más fuerte que las otras tres estructuras. Esto significa que LSPR se puede excitar de manera más eficiente en la estructura original, lo que da como resultado un FWHM más estrecho y una caída de reflectividad menor.
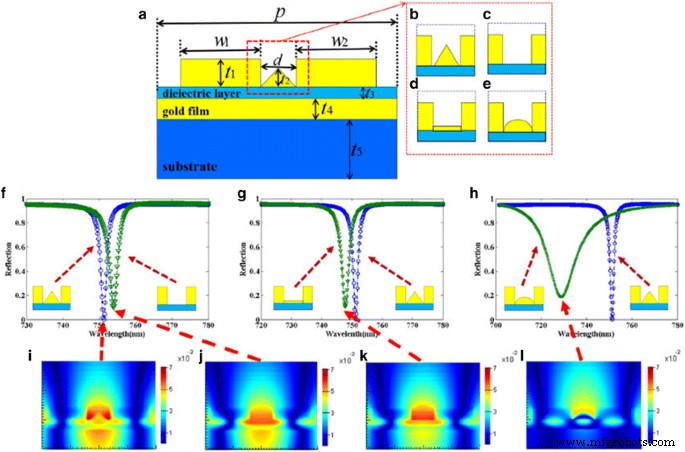
a – e Esquema del metamaterial propuesto con diferentes nanoestructuras de una celda unitaria. f – h Espectros de reflexión de las diferentes estructuras. i – l Distribuciones del campo magnético H en el pico resonante de las estructuras correspondientes
De la Fig. 5, el rendimiento óptico de la estructura original con el uso de nanocintas triangulares es superior al de las otras estructuras. Con el fin de comprender mejor las influencias de las nanocintas triangulares en el rendimiento óptico, proporcionamos un cálculo y un análisis detallados de la estructura modificada que se muestra en la Fig. 6a, que contiene una nanocinta trapezoidal con un mismo ángulo θ a la nanocinta triangular en la estructura original. En primer lugar, como se muestra en la Fig. 6b, c, investigamos el rendimiento óptico de la estructura modificada dependiendo de las diferentes alturas h de la nanocinta trapezoidal cuando los ángulos θ permanece inalterable. Obviamente, cuando la altura h es superior a 10 nm, el rendimiento óptico de la estructura se mantendrá casi sin cambios, lo que demuestra que el rendimiento óptico de la estructura es robusto en la fabricación. A medida que la altura h está por debajo de 5 nm, la caída de reflectividad aumenta, lo que puede explicarse que la altura h es demasiado pequeño que reduciría el área efectiva de excitación de LSPR. Como se muestra en la Fig. 6d, e, también investigamos el rendimiento óptico de la dependencia de la estructura modificada en diferentes ángulos θ cuando la altura h se establece en 15 nm. Es fácil observar que el rendimiento óptico de la estructura modificada cambia poco con el amplio rango de ángulos de 35 ° a 68 °. Sin embargo, la caída de la reflectividad aumenta obviamente en el ángulo θ menor que 30 °, lo que puede entenderse que el ángulo demasiado pequeño θ puede reducir la eficiencia de excitación de LSPR. Por lo tanto, mediante el análisis detallado de las influencias de los diferentes parámetros de los ángulos entre la nanocinta trapezoidal y las nanocintas cuadradas sobre el rendimiento óptico, el rendimiento de absorción perfecto de la estructura original se atribuye a la excitación de LSPR en la esquina entre la nanoribona triangular. y las nanocintas cuadradas, que concuerda bien con los resultados del campo magnético que se muestra en la Fig. 5i. Al mismo tiempo, la estructura puede mantener un buen rendimiento óptico en una amplia gama de alturas h y ángulos θ , lo que sugiere una gran relajación de la robustez de la fabricación y hace que la nanoestructura se vuelva más realista en el punto de vista experimental. Finalmente, considerando los procesos de fabricación de la nanoestructura real, la Fig. 6f muestra la geometría de la estructura con la rugosidad de la superficie de oro / dieléctrico y el tratamiento de pasivación para todos los ángulos agudos. La comparación del rendimiento óptico entre la estructura modificada y la estructura original se calcula y representa en la Fig. 6g. Obviamente, el efecto de la tolerancia de fabricación sobre el rendimiento de la nanoestructura es muy pequeño, lo que muestra el robusto rendimiento óptico en la fabricación.
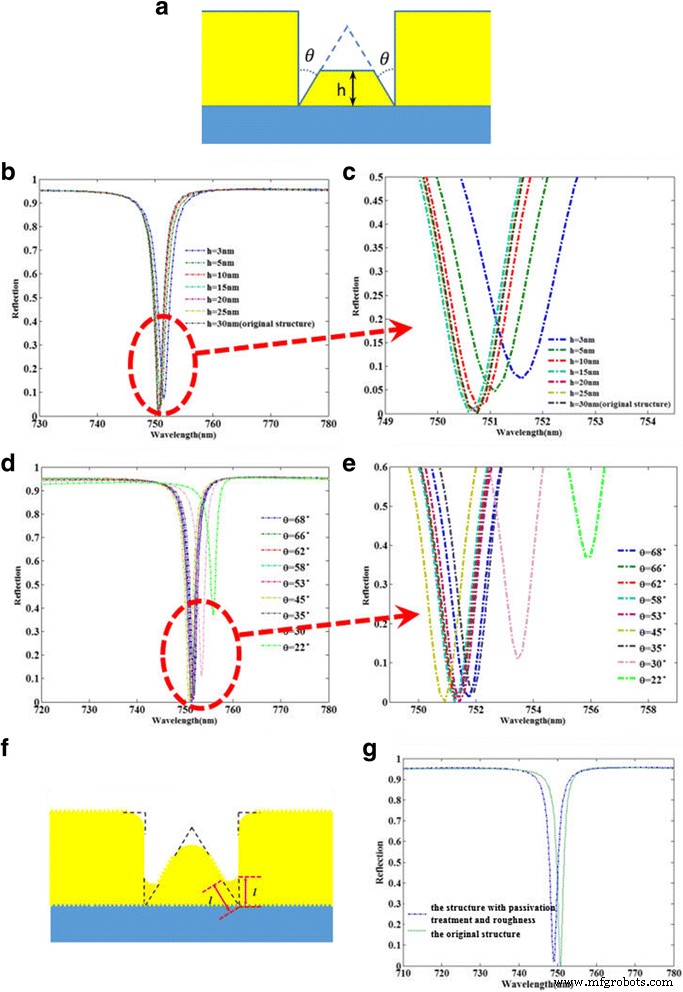
un La estructura modificada que contiene una nanocinta trapezoidal con el mismo ángulo θ a la nanocinta triangular. b , c Comparación de espectros de reflexión entre las nanoestructuras con diferentes alturas h , cuando el θ mantener sin cambios. d , e Comparación de espectros de reflexión entre las nanoestructuras con diferentes ángulos θ , cuando la altura h =15 nm. f La estructura modificada con la rugosidad de la superficie de oro / dieléctrico y el tratamiento de pasivación para todos los ángulos agudos. g Comparación de espectros de reflexión entre la estructura modificada y la estructura original, cuando el l está configurado como 3 nm
Luego, también investigamos los efectos de la dimensión de la estructura y los parámetros del material, utilizando el método FDTD, sobre la reflectividad del buzamiento, FWHM y la longitud de onda de resonancia de la estructura diseñada. Se estudiarán varios parámetros, incluido el índice de refracción del dieléctrico, ancho de nanocintas de oro w , el ancho de nanocintas de oro d y el grosor de las nanocintas de oro t 1 . La figura 7 muestra el efecto del índice de refracción de la capa dieléctrica sobre el espectro de reflectancia de la estructura del metamaterial. Como se muestra en la Fig. 7a, la longitud de onda de resonancia se desplaza al rojo obviamente al aumentar n dieléctrico , que es consistente con la predicción del modelo de circuito LC. Como se muestra en la Fig. 5b, la caída de la reflectividad disminuye primero y luego aumenta cuando el n dieléctrico aumenta, mientras que FWHM se vuelve más estrecho. El FWHM y la caída de reflectividad del espectro de reflexión dependen en gran medida de la fuerza de acoplamiento entre las nanocintas y la película de oro, lo que da como resultado los diferentes rendimientos ópticos con varios materiales dieléctricos del espaciador dieléctrico entre las nanocintas y la película de oro. La caída de la reflectividad es el valor mínimo cuando el índice de refracción de la capa dieléctrica es aproximadamente 1.3. Al mismo tiempo, el FWHM es de alrededor de 1,85 nm, que es mucho más estrecho que el del absorbente de banda estrecha publicado en la región visible [24, 28, 34, 39].
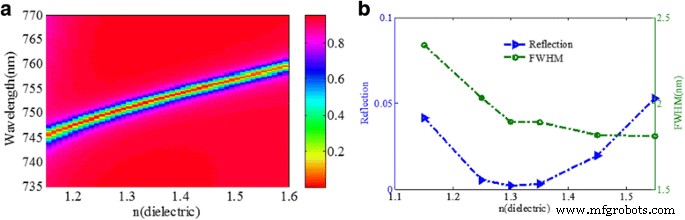
un Espectros de reflexión en función del índice de refracción de la capa dieléctrica. b Reflectividad de la caída de resonancia y FWHM en función del índice de refracción de la capa dieléctrica
La Figura 8 presenta la influencia del ancho de nanocintas de oro w en el espectro de reflexión de la estructura del metamaterial. Como se muestra en la Fig. 8a, cuando el ancho de nanocintas de oro w cambia de 140 a 177 nm, la longitud de onda resonante cambia al azul, lo que concuerda bien con los resultados del modelo de circuito LC equivalente. La Figura 8b muestra que FWHM se vuelve más estrecho y la caída de la reflectividad aumenta con el aumento de w . El aumento de la caída de la reflectividad puede resultar del aumento del área de metal efectiva para reflejar la luz incidente, con un aumento de w . Los valores mínimos de caída de reflectividad y FWHM no se pueden obtener simultáneamente. Sin embargo, en nuestro diseño, tanto los valores de la caída de reflectividad como el FWHM cambian ligeramente en un amplio rango de w (140 ~ 162 nm), que es favorable para aplicaciones prácticas.
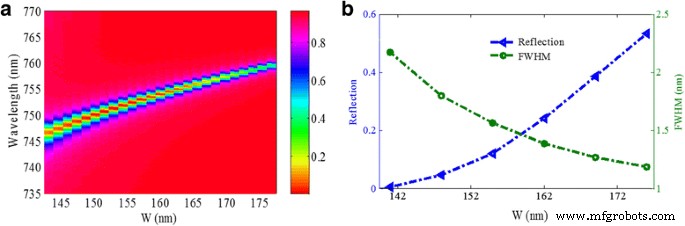
un Espectros de reflexión en función del ancho de las nanocintas de oro w . b Caída de reflectividad y FWHM como funciones del ancho de las nanocintas de oro w
Además, como se muestra en la Fig. 9a, la caída de la reflectividad puede mantener un valor más bajo cuando el ancho de la nanocinta de oro d está entre 55 y 75 nm mientras que aumenta obviamente cuando d excede los 76 nm, lo que puede explicarse que una distancia demasiado grande entre las dos nanocintas puede reducir la eficiencia de excitación para LSPR, reduciendo así la eficiencia de absorción de la luz incidente. El FWHM se vuelve más estrecho al aumentar d y el tamaño óptimo de d es de alrededor de 75 nm. A partir de la Fig. 9b, la caída de la reflectividad puede mantener un valor más bajo cuando el espesor de la nanocinta de oro t 1 cambia de 35 a 50 nm mientras que el FWHM se vuelve más estrecho. Sin embargo, cuando t 1 aumenta de 50 a 60 nm, la caída de la reflectividad aumenta obviamente. Podemos entender el resultado de esta manera, la nanocinta es demasiado gruesa que aumentaría el reflejo de la luz incidente. La Figura 9c muestra que el valor mínimo de la caída de resonancia se obtiene cuando la altura triangular del oro t 2 es de alrededor de 30 nm. En esta estructura, la caída de la reflectividad ha estado por debajo de 0.025 cuando la altura del oro triangular varía de 15 a 40 nm, lo que es beneficioso para diseñar estructuras de metamateriales debido al excelente rendimiento de robustez.
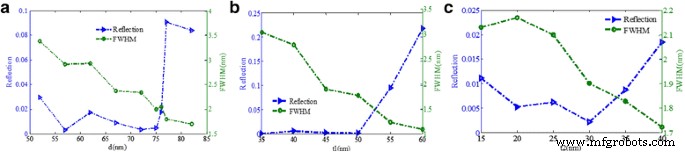
un Descenso de reflectividad y FWHM como funciones del ancho triangular de nanocintas de oro d . b Descenso de reflectividad y FWHM como funciones del espesor de nanocintas de oro t 1 . c Reflectividad del buzamiento de resonancia y FWHM como funciones de la altura triangular del oro t 2
En general, se sabe que la longitud de onda resonante de la estructura del metamaterial depende en gran medida del índice de refracción del medio ambiental, que se ha utilizado ampliamente en aplicaciones de detección. La Figura 10a muestra que la longitud de onda resonante se desplaza al rojo obviamente cuando aumenta el índice de refracción del entorno, lo que está de acuerdo con la predicación del modelo LC, y la caída de la reflectividad puede mantener un valor extremadamente bajo al mismo tiempo. Cuando el RI aumenta de 1.07 a 1.12, la longitud de onda resonante cambia de 733.828 a 755.097 nm. La sensibilidad de longitud de onda calculada ( S ) es de aproximadamente 425 nm / RIU, y FWHM puede ser tan estrecho como 1,82 nm. Así, el FOM puede llegar a 233,5. Hasta donde sabemos, el FOM es mucho más alto que el del sensor de índice de refracción plasmónica publicado anteriormente en la región visible [24, 28, 34, 39]. El sensor de índice de refracción plasmónico propuesto muestra una buena linealidad, como se muestra en la Fig. 10b.
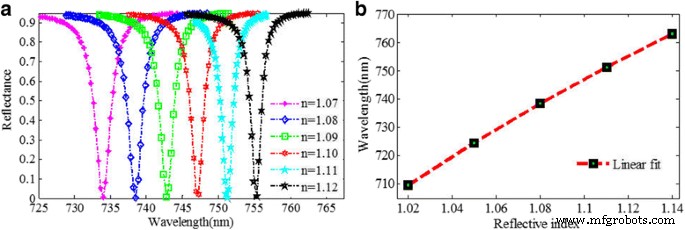
un Espectros de reflexión del sensor de índice de refracción plasmónico con varios índices de refracción del medio ambiente. b Cambio de longitud de onda resonante contra el índice de refracción circundante
En aplicaciones prácticas, generalmente es necesario detectar el cambio de intensidad relativa a una longitud de onda fija con los diversos índices de refracción del medio circundante, y la figura de mérito correspondiente se define como FOM * =max | ( dI / dn ) / yo | [17]. Como se muestra en la Fig. 11a, el FOM * cambia obviamente al disminuir w , y el máximo de FOM * puede alcanzar 1,4 × 10 5 en el w de alrededor de 358 nm. La Figura 11b muestra que el FOM aumenta al disminuir d y se obtiene un máximo de FOM * en d =75 nm. Como se muestra en la Fig. 11c, cuando el grosor de las nanocintas de oro t 1 es de 35 nm, el FOM * es el máximo. Además, la Fig. 11d también muestra que el máximo de FOM * se obtiene cuando la altura triangular del oro t 2 es de unos 30 nm. Las características del FOM y FOM * con los cambios de las dimensiones de la estructura se investigan numéricamente, lo que puede ofrecer cierta orientación para diseñar un sensor plasmónico de alto rendimiento.
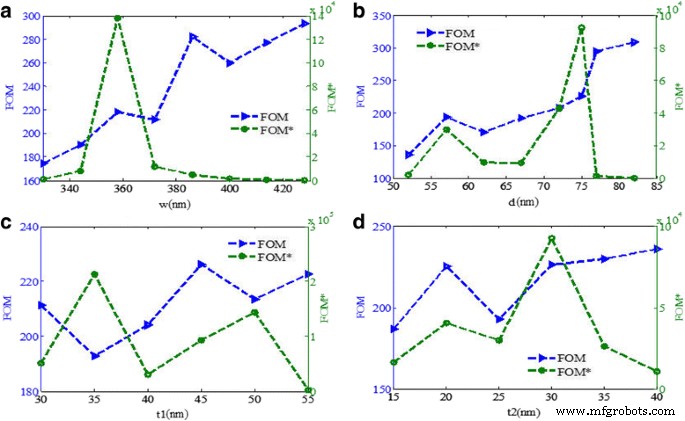
a – d FOM y FOM * como funciones del ancho de nanocintas de oro w , el ancho triangular de nanocintas de oro d , el grosor de las nanocintas de oro t 1 y la altura triangular de oro t 2 , respectivamente
Conclusiones
En resumen, proponemos y demostramos numéricamente un absorbente de banda ultra-estrecha casi perfecto con una absorción que alcanza el 95% en la región visible. Además, realizamos un análisis detallado de las influencias de la forma estructural y las dimensiones estructurales en las propiedades ópticas de la estructura del metamaterial mediante el uso de FDTD bidimensional. Utilizando las dimensiones optimizadas de la estructura, presenta una caída de reflectividad tan baja como 0,001 con la FWHM de 1,82 nm con incidencia normal en la región visible. Además, también demostramos su capacidad de detección. Su sensibilidad ronda los 425 nm / RIU y el FOM puede llegar a 233,5. This is much better than that of the previously reported sensor in visible region [24, 28, 34, 39]. For its high sensing performance, the metamaterial structure may be found applications in the biological binding, integrated photodetectors, chemical applications, and so on.
Abreviaturas
- FDTD:
-
Finite-difference time-domain
- FOM:
-
Figure of merit
- FWHM:
-
Full width at half maximum
- LSPR:
-
Localized surface plasmon resonance
- MDM:
-
Metal-dielectric-metal
- S:
-
Sensitivity
- TM:
-
Transverse magnetic
Nanomateriales
- Aplicación del molibdeno y sus aleaciones
- ¿Qué es la calibración del sensor? Definición y su aplicación
- Qué es un sensor de distancia en funcionamiento y sus aplicaciones
- Qué es un sensor IMX586:funcionamiento y sus características
- Qué es el funcionamiento del sensor de peso y sus especificaciones
- Funcionamiento del sensor virtual y sus aplicaciones
- Funcionamiento del sensor de voltaje y sus aplicaciones
- Sensor Lambda - Funcionamiento y sus aplicaciones
- Funcionamiento del sensor IMU y sus aplicaciones
- El funcionamiento del sensor de imagen y sus aplicaciones
- La historia del aserrado de cinta y sus ideas innovadoras



