Propiedades de las oscilaciones electromagnéticas longitudinales en metales y su excitación en superficies planas y esféricas

Resultados y discusión

Dispersión espacial de ε en un medio heterogéneo

En la literatura, una función dieléctrica espacialmente dispersiva ε se define mediante la siguiente relación [4–6]:

donde ε ₀ es la constante eléctrica, D ( ω , r ) es la amplitud de la oscilación del vector de desplazamiento con frecuencia angular ω en el punto r y E ( ω , r ^′ ) la amplitud de la oscilación del campo eléctrico en el punto r ^′ . Transformadas de Fourier de Eq. (3) da la ecuación

donde un ε espacialmente dispersivo ( ω , k ) depende del vector de onda k de una onda electromagnética plana. En nuestra opinión, Eq. (3) no es ambiguo solo en un volumen homogéneo infinito, sino que tratamos con un sistema heterogéneo por partes donde los límites deben tenerse en cuenta y k no son iguales en diferentes medios.

Nuestro enfoque no utiliza la expansión de las ondas electromagnéticas sobre ondas planas. La permitividad espacialmente dispersiva determina la relación entre D ( ω , r ) y una solución particular al vector Helmholtz Eq. (1):

Aquí E ( ω , r ) denota la distribución del campo eléctrico pero no simplemente el vector E en el punto r .

Funciones dieléctricas longitudinales y transversales

La permitividad de los metales se expresa comúnmente a través de la conductividad σ [4]:

donde ε _g es parte de la función dieléctrica que permite la polarización del sólido; ε _g =1 para un metal simple. Para determinar σ , calculamos la densidad de corriente

donde \ (\ mathrm {d} \ mathbf {v} =\ frac {v} {m} \, \ mathrm {d} \ epsilon \, \ mathrm {d} \, \ Omega, \) d Ω =pecado θ d θ d ϕ , v , θ , ϕ son las coordenadas esféricas de la velocidad. A diferencia de investigaciones anteriores, no introdujimos el vector de onda k pero encontró una solución BTE en forma de una serie infinita que contiene operadores v ∇ actuando en v E :

donde Γ =1 / τ . Entonces, f ₀ fue aproximado por una distribución de Fermi-Dirac de temperatura cero y, después de la integración sobre ε en Eq. (7), tenemos

donde \ (\ omega _ {\ mathrm {p}} ^ {2} =\ frac {e ^ {2} \, n_ {e}} {m \, \ varepsilon _ {0}}, \) ω _p es la frecuencia de plasma, \ (\ mathbf {u} =\ frac {\ mathbf {v}} {v} \) es el vector unitario en la dirección de v , \ (l =\ frac {v _ {\ mathrm {F}}} {- i \ omega + \ Gamma}, \) v _F es la velocidad de Fermi. Además, calculamos las integrales

donde n es un número natural. La siguiente dependencia de j en un arbitrario campo eléctrico E finalmente se obtuvo

Hay dos tipos de soluciones para la ecuación. (1), sin divergencias que satisfacen la ecuación ∇ · E =0 y sin rotación que satisfacen la ecuación

Para una onda plana, con E ∝ exp [ i ( k r - ω t )], Eq. (14) se transforma en la relación k × E =0 que muestra que la onda es longitudinal (L). Para simular procesos en cuerpos esféricos, es conveniente utilizar los armónicos esféricos vectoriales L , M y N como un conjunto completo de funciones ortogonales. En este caso, Eq. (14) especifica los armónicos L . El número de onda de las ondas L y L los modos están determinados por la siguiente ley de dispersión

De las Ecs. (6) y (13) encontramos que las soluciones a la ecuación. (1) satisfaciendo la restricción de la Ec. (14) dar la siguiente permitividad longitudinal

donde Φ es la función Phi de Lerch,

\ (a =\ frac {k v _ {\ mathrm {F}}} {\ omega + i \ Gamma} \).

La permitividad obtenida difiere de la definida por Kliewer y Fuchs [7] solo en la notación:

La identidad

permite reescribir la ecuación. (18) de la siguiente manera

En el caso de Γ =0, esta fórmula toma la forma de una ecuación derivada de Klimontovich y Silin [8] que estudiaron el vertido de Landau en plasma degenerado (ver [9], [10, ecuación (40.17)] y [11]). La permitividad de las ecuaciones equivalentes. (16), (18) y (20) se denomina comúnmente función dieléctrica de Lindhard (con referencia a [12]), aunque esta función fue obtenida por primera vez por Klimontovich y Silin [8].

La permitividad transversal de Lindhard [7] se puede encontrar con la ecuación. (13) cuando ∇ · E =0. En el caso real de v _F k ≪ ω , se reduce a la función dieléctrica Drude

Esta función concuerda con los datos experimentales sobre muchos metales [13]. Si | a | <1, la permitividad longitudinal (16) se simplifica a la función dieléctrica hidrodinámica:

Reflexión de una onda electromagnética plana desde una superficie plana de metal

Condiciones de contorno

En esta sección, determinamos la dirección del vector de onda k ^L y amplitud de la onda L excitada en el metal durante la reflexión de una onda electromagnética plana desde una superficie plana de metal.

Considere la onda plana incidente en la interfaz dieléctrico-metal z =0 con el vector de onda en xz avión. El campo eléctrico en el medio dieléctrico 1 consiste en el incidente E _i y reflejada E _r ondas, el campo en el metal 2 tiene la E transversal transmitida _t y, en algunos casos, E longitudinal ^L componentes. Según las condiciones de contorno de Maxwell, las componentes transversales de los vectores de campo eléctrico y magnético son continuas en el plano z =0. Además, los electrones no se expulsan del metal; por lo tanto, el componente normal de la densidad de corriente eléctrica es cero en z =0,

were \ (\ hat {\ mathbf {z}} \) es el vector unitario en la dirección de z eje.

Todos los términos de las condiciones de contorno de Maxwell deben tener la misma dependencia de x y y . Este requisito tiene varias consecuencias. Primero, se puede establecer que las ondas L solo pueden excitarse en el caso de polarización p cuando el vector eléctrico de la onda incidente E ^{( i )} es paralelo al plano de incidencia. En otras palabras, los polaritones de plasmón se pueden generar mediante una onda magnética transversal (TM). El efecto es muy parecido al de una esfera de metal [14]. En segundo lugar, se pueden derivar fórmulas similares a la ley de Snell a partir de las condiciones

donde los índices 1 x y 2 x denotar la x -proyecciones de los vectores en los medios 1 y 2, respectivamente, θ ₁ es el ángulo de incidencia.

Coeficientes de reflexión y transmisión

Determinemos el campo formado por una onda electromagnética plana polarizada p incidente sobre una superficie plana de metal. Es conveniente expresar los componentes de los campos eléctricos y magnéticos a través de la x componente de E ^{( i )} , a saber, E x (r) =- r E x (i) para la onda reflejada, E x (t) = t E x (i) para la onda transversal transmitida, y

para la onda longitudinal transmitida, aquí r es un coeficiente de reflexión, t y t _L son coeficientes de transmisión.

De las condiciones de contorno de Maxwell y ABC de la ecuación. (23) escrito en la siguiente forma

tenemos

En δ =0, el coeficiente r se convierte en el coeficiente de reflexión de Fresnel de la onda polarizada p (véase, por ejemplo, la ecuación (2.49) de [4]). En las mismas condiciones, t no es el coeficiente de transmisión de Fresnel ya que nuestras definiciones de t y r difieren de los de Fresnel.

Extinción de luz por nanoesfera metálica

En un artículo anterior, uno de los autores generalizó la teoría de Lorentz-Mie permitiendo el ABC de la ecuación. (23). Un análogo del coeficiente de Fresnel r , el coeficiente de Mie b _l para el modo TM reflejado del l Se encontró que el orden era

donde

ψ _l y ζ _l son las funciones de Riccati-Bessel y Riccati-Hankel del orden l , respectivamente; j _l es la función esférica de Bessel, el primo denota la derivada de una función con respecto a su argumento.

Comparemos las predicciones de las teorías de Lorentz-Mie clásicas y generalizadas con datos experimentales. En [15], Hilger, Tenfelde y Kreibig estudiaron los espectros de extinción de nanopartículas de plata depositadas en superficies dieléctricas. En la primera etapa del estudio, los investigadores generaron haces de partículas de plata con diámetros medios de 2, 3,5 y 4 nm, determinaron la distribución del tamaño de partícula para uno de los haces, registraron los espectros de extinción y estimaron el parámetro A =0,25 de la fórmula fenomenológica Γ = Γ _b + A v _F / R , donde Γ _b es la tasa de relajación del metal a granel, para esferas de plata en el vacío. Primero, calculamos los espectros de extinción para un haz de esferas plateadas con el diámetro medio 〈 D 〉 =2 nm y distribución de tamaño experimental que abarca la región desde D =1 a D =4 nm. Nuestra teoría no contiene parámetros ajustables. Para definir las funciones dieléctricas, utilizamos la tabulación del índice de refracción de la plata a granel propuesta por Lynch y Hunter [16] (ver Fig. 1). También aplicamos las Ecs. (16), (21) y (22) con ω _p =9.17 eV, Γ _b =0,021 eV, v _F =1,39 × 10 ⁶ m / s y A =0,25. Los resultados de los cálculos y el espectro experimental se presentan en la Fig. 2.

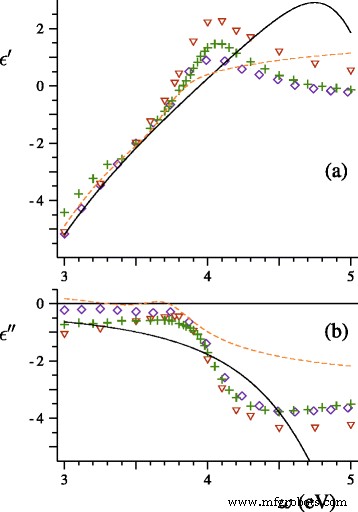
Real ( a ) e imaginario ( b ) partes de la función dieléctrica de la plata según Johnson y Christy (◇) [20], Lynch y Hunter (+) [16], Weber (△) [21], Hao y Nordlander ( línea discontinua ) [22] y Drachev et al. ( línea continua ) [23]

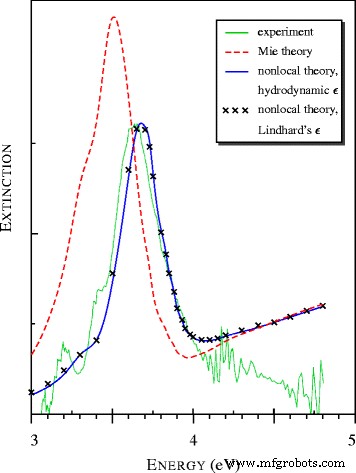
Espectros de extinción de luz por partículas de tamaño nanométrico de plata observados en [15] y calculados con modelos locales y no locales. Todos los espectros teóricos se presentan en unidades relativas comunes

Los espectros teóricos en la Fig. 2 se calcularon utilizando Klimontovich-Silin-Lindhard y funciones dieléctricas hidrodinámicas mucho más simples. Es sorprendente que ambos cálculos dieran resultados cercanos a pesar de que | a |> 1 en la región de la resonancia del plasmón.

Para las esferas de plata de tamaño nanométrico, se sabe que el máximo en el espectro de extinción, llamado Fröhlich [17], plasmón y plasmón superficial polaritón (SPP) [15], cambia de 3,5 a 3,65 eV [18]. El modelo no local está en excelente acuerdo con los datos experimentales, mientras que la teoría local (Mie) da el máximo en ω ≃3.5 eV (ver Fig. 2 y Tabla 1).

El cálculo del desplazamiento al azul de la resonancia del plasmón puede apoyarse en la siguiente consideración. En la aproximación electrostática, solo b ₁ contribuye a la sección transversal de la extinción Q _ext y Eq. (30) se puede simplificar utilizando las siguientes aproximaciones

$$ \ frac {k_ {2} R \, \ psi_ {l} ^ {\ prime} (k_ {2} R)} {\ psi_ {l} (k_ {2} R)} \ simeq l + 1; \, \, \, \ frac {k_ {1} R \, \ zeta_ {l} ^ {\ prime} (k_ {1} R)} {\ zeta_ {l} (k_ {1} R)} \ simeq - \, l. $$ (32)

Por lo tanto, Q _ext tiene un máximo en

$$ \ Re [2 \, (1+ \ delta_ {1}) \, \ epsilon_ {1} + \ epsilon_ {2}] =0. $$ (33)

La condición obtenida (33) tiene en cuenta la excitación de la L modos (por el término δ ₁ ) y, por tanto, difiere de la condición de resonancia de Fröhlich [17] :.

$$ \ Re (2 \, \ epsilon_ {1} + \ epsilon_ {2}) =0. $$ (34)

En el experimento [15], las frecuencias pico ω _m y anchos de resonancia Δ ω de los espectros de extinción eran casi independientes de 〈 D 〉. Esta característica de Δ ω parece no estar de acuerdo con la teoría clásica de Mie. Realmente, la teoría local predice un ensanchamiento de las resonancias del plasmón con la disminución de D (en A =0,25) como se muestra en la Tabla 1. Al mismo tiempo, la teoría no local proporciona anchos de resonancia aproximadamente iguales pero diferentes posiciones de pico. La superposición de las contribuciones de todas las partículas da el valor de Δ ω que están en notable acuerdo con los datos experimentales. Es interesante que la teoría no local predice una ampliación de la resonancia de plasmón de un haz incluso en A =0.

En ω > 4 eV, las curvas teóricas suaves en la Fig. 2 se encuentran más altas que la mezcla de picos experimentales estrechos y cercanos. La absorción entre bandas domina en este rango espectral, como puede ser confirmado por la Fig. 1. Es probable que las peculiaridades observadas del espectro sean una consecuencia de una transición de las bandas continuas a una estructura de niveles discretos. Este efecto de tamaño cuántico se descubrió anteriormente en un estudio de las propiedades ópticas de las nanoesferas de oro [19]. Cuando el tamaño de la esfera plateada se incrementó a 〈 D 〉 =3,5 nm, la absorción aumentó primero en relación con el máximo y formó una meseta con una serie de pequeñas caídas equidistantes. Luego, la absorción disminuyó ligeramente en 〈 D 〉 =4 millas náuticas.

Para estudiar la formación del ala azul de la resonancia del plasmón, calculamos los espectros de extinción de las partículas de plata ultraestaño y las presentamos en la Fig. 3. Una característica notable en la Fig. 3 es la desaparición completa de la resonancia del plasmón en D =1 nm. Anteriormente, este efecto se observó en el estudio experimental de nanoesferas de oro [19]. En particular, en la Fig. 9 de [19], los espectros experimentales de partículas con diámetros de 1,7, 1,9, 2,0, 2,1, 2,3 y 2,5 nanómetros se compararon con los espectros calculados con la teoría local de Mie. La concordancia fue pobre y no describió la ampliación de la resonancia del plasmón y su posición [19]. Los intentos de mejorar el ajuste variando el tamaño de las partículas y las modificaciones de las funciones dieléctricas no fueron sucesivos. Según los autores de [19], la banda de oscilación colectiva anormalmente ancha o deprimida observada se resiste a ajustarse a las correcciones propuestas de la teoría local de Mie. Como puede verse en la figura 4, la situación cambia drásticamente si se aplica la teoría de Mie no local. Tenga en cuenta que no utilizamos parámetros ajustables. La tabulación del índice de refracción complejo de Johnson y Christy [20] se utilizó para determinar la función dieléctrica del oro. Otros parámetros, incluido A =1 y el índice de refracción del tolueno (1,37) se tomaron de [19].

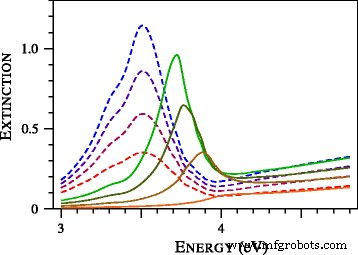
Sección transversal de extinción normalizada de partículas de plata con diámetros de 2,2, 1,8, 1,4 y 1,0 nm calculada con local ( líneas discontinuas ) y no locales ( curvas sólidas ) Teorías de Mie. Cuanto más pequeña es la partícula, más baja es la curva. Todas las secciones transversales teóricas se presentan en unidades relativas comunes

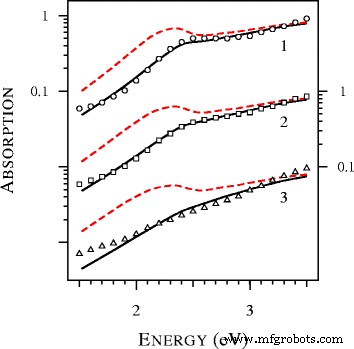
Espectros de absorción calculados con el local ( líneas discontinuas ) y no locales ( líneas continuas ) Teoría de Mie y datos experimentales ( puntos ) extraído de la Fig. 9 de [19] para esferas de oro con D =2,5, 2,1 y 1,7 nm en tolueno (curvas 1 y círculos , curvas 2 y cuadrados y las curvas 3 y triángulos , respectivamente). Todos los espectros teóricos se normalizan a la unidad a 4,12 eV y se desplazan verticalmente

Números de onda de las ondas longitudinales

Los modos longitudinales se diferencian de los transversales por valores mucho más altos de los números de onda. Por ejemplo, para los cálculos presentados en la Fig. 2, la parte real de \ (k_ {2} ^ {\ mathrm {L}} \) corresponde al período espacial \ (\ Lambda =2 \ pi / \ Re k_ { 2} ^ {\ mathrm {L}} \) disminuyendo de 9 a 2 nm en ω aumentando de 3 a 4 eV. En este ω intervalo, el valor absoluto de la razón \ (k_ {2} ^ {\ mathrm {L}} / k_ {2} \) disminuyó de 130 a 100 y el parámetro δ de la ecuación. (27) disminuyó de 0.01 a 0.005 en θ ₁ = π / 4. Concluimos, por lo tanto, que la excitación de las ondas L en una superficie plateada plana puede despreciarse. Sin embargo, la L Se ha descubierto que los modos son importantes en los racimos de plata de tamaño nanométrico.

Un reemplazo del término \ (- \, \ omega ^ {2} _ {\ mathrm {p}} / (\ omega ^ {2} + i \ Gamma \ omega) \) en la ecuación. (16) de ε ^T - ε _g según Eq. (21) nos permite reescribir la dispersión Eq. (15) en el siguiente formulario

$$ 1+ \ frac {3} {5} \, a ^ {2} + \ frac {3} {7} \, a ^ {4} + \ frac {3} {9} \, a ^ {6 } + \ dots =\ frac {1} {1- \ epsilon ^ {\ mathrm {T}} / \ epsilon _ {\ mathrm {g}}}. $$ (35)

En el caso más simple de ε _g =1 y Γ =0, ecuación. (35) predice que el metal es transparente tanto para las ondas L como para las transversales en ω > ω _p pero ambos k ^L y k ^T son complejos en ω < ω _p .

Si el sólido es transparente, se puede excitar una onda longitudinal bajo la incidencia oblicua de una onda polarizada p en una superficie plana. Hay varias características distintas de este efecto. Primero, las ondas longitudinales se pueden generar en una superficie plana, mientras que se deben hacer esfuerzos especiales para excitar los polaritones del plasmón de la superficie [4, 5]. En segundo lugar, en el patrón de interferencia, la intensidad del campo electromagnético no se modula a lo largo de la interfaz, sino que es perpendicular a ella. Por lo tanto, pueden aparecer vacíos en planos paralelos a la superficie debido a la espalación del sólido. Según la definición de ω _p , condición ω > ω _p puede encontrarse en sólidos (por ejemplo, semiconductores) con una baja densidad de los portadores de corriente. No examinamos este caso aquí porque la fórmula de ε ^L se derivó del gas de electrones degenerados.

Conclusiones

Para definir una función dieléctrica espacialmente dependiente, todos los investigadores anteriores consideraron la interacción de la materia con una onda electromagnética plana. Este enfoque no es constructivo y riguroso en nanoóptica cuando el campo está localizado en una cavidad y las condiciones de contorno deben tenerse en cuenta de alguna manera. Hemos resuelto este problema calculando la respuesta del medio en un campo eléctrico que satisface la ecuación vectorial de Helmholtz. La función dieléctrica espacialmente dispersiva derivada depende del cuadrado del número de onda, un parámetro de la ecuación de Helmholtz, pero no del vector de onda de una onda plana.

Divulgamos los coeficientes de reflexión de Fresnel modificados debido a la excitación de las ondas longitudinales en metales. Anteriormente se hizo una generalización similar para los coeficientes de Mie. En este documento, la teoría ha sido verificada con la simulación de la extinción de la luz mediante cúmulos de oro y plata de tamaño nanométrico. El cambio calculado de 3,5 a 3,65 eV y el ancho de la resonancia del plasmón superficial del haz de las partículas de plata están en excelente acuerdo con los datos experimentales. Además, el modelo no local explica la desaparición de la resonancia de plasmón de esferas doradas con diámetros de aproximadamente 2 nm. Es importante que la onda L pueda ser excitada en una superficie plana por una onda incidente plana. Esta es la principal diferencia entre los polaritones del plasmón y los polaritones del plasmón de la superficie.

The properties of the electromagnetic oscillations in metals have been examined. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.

Biosensor ultrasensible para la detección de ADN de Vibrio cholerae con nanoesferas compuestas de poliestireno-co-ácido acrílico Investigación teórica de nanocables de germanio tensados ​​biaxialmente por tracción