El diseño de la capa conductora AZO en placa de microcanal

Introducción

La placa de microcanal (MCP) es un multiplicador de electrones compuesto por matrices de poros bidimensionales por integración de forma de placa de vidrio delgada, longitud de 0,5 a 5 mm, un diámetro de 4 a 40 μm y con un ángulo de polarización generalmente de 5 ° a 13 ° con respecto a la normal. de la superficie de la placa; la proporción de área abierta de la placa es de hasta 60%, y la proporción alta de longitud a diámetro en cada poro es de aproximadamente 20:1 a 100:1 [1].

Como se muestra en la Fig. 1, los electrones incidentes que ingresan al microcanal chocan con las paredes, lo que hace que se generen electrones secundarios en la superficie de las paredes del microcanal. Las colisiones múltiples con las paredes del microcanal conducirán a un número creciente de electrones secundarios, lo que resultará en una avalancha de electrones dentro del microcanal y la emisión de una nube de electrones desde la salida del microcanal. Los electrones de electrones secundarios se acelerarán aún más a lo largo del microcanal mediante un voltaje de polarización. La ganancia de MCP es 10 ³ –10 ⁴ a una tensión de trabajo 700–900 V [2,3,4,5,6,7,8,9].

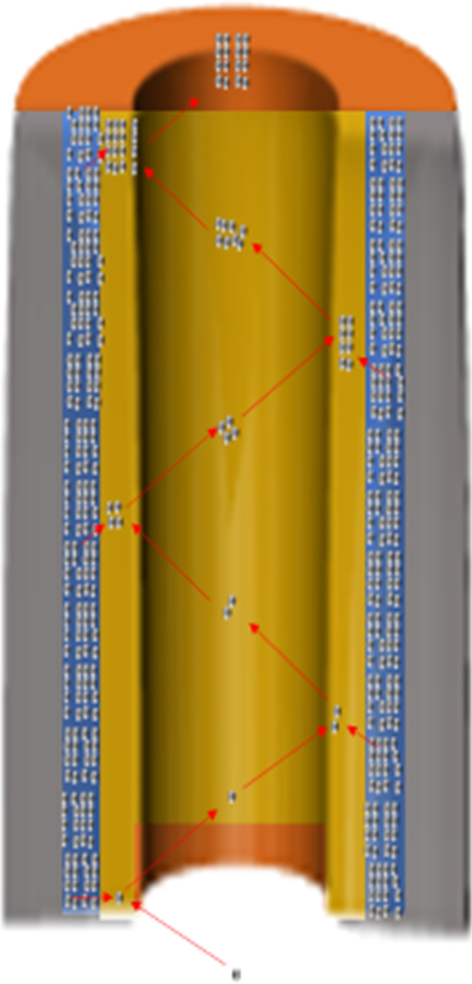
Diagrama de estado de trabajo de MCP

Cada microcanal es un detector y un multiplicador de electrones. Al tener millones de microcanales trabajando de forma independiente, MCP tiene las características de alta resolución espacial, alta resolución de tiempo y amplio rango de ganancia utilizado para identificar los fotones, electrones, neutrones e iones. El MCP se puede integrar en varios tipos de instrumentos, incluido el detector fotoeléctrico, los tubos fotomultiplicadores (PMT), el espectrómetro ultravioleta, el tubo de rayos catódicos, el microscopio electrónico de barrido, las pantallas de emisión de campo, el analizador de gases residuales, las imágenes médicas, la espectrometría de masas de tiempo de vuelo, la noche -gafas de visión, etc. [1, 4, 7,8,9]. La combustión de hidrógeno del proceso tradicional hace que el microcanal tenga una conductividad adecuada y un coeficiente de emisión de electrones secundarios.

El proceso habitual de combustión con hidrógeno en la preparación de un microcanal tiene muchas deficiencias:primero, el proceso de combustión con hidrógeno no puede ajustar independientemente la capa conductora y la capa de emisión [10, 11]; en segundo lugar, los elementos de metales pesados ​​(Pb, Bi) provocan contaminación ambiental en el proceso de fundición del vidrio con plomo; tercero, grandes áreas de MCP se deformarán debido a la alta temperatura [8]; cuarto, el vidrio de plomo que se utiliza en la reacción de reducción de hidrógeno contiene K, Rb y otros elementos radiactivos que producen ruido de fondo [8]; Por último, el hidrógeno que queda en los poros se convierte en iones debido al voltaje de polarización y volará en la dirección opuesta al electrón para destruir el cátodo del instrumento [8, 12].

Los primeros científicos proponen una solución para hacer crecer la capa conductora y la capa de emisión en la pared del microcanal para reemplazar el proceso de combustión de hidrógeno [3]. Muchos métodos de deposición de película delgada no pueden hacer crecer una película uniforme en el microcanal con relaciones de largo a diámetro altas. El laboratorio nacional Argonne propuso utilizar la deposición de capa atómica (ALD) para hacer crecer la capa conductora y la capa de emisión en el MCP para lograr una película intacta y uniforme en las paredes del microcanal [4, 13]. Además, ALD-MCP resuelve las deficiencias mencionadas anteriormente. Muchas instituciones de investigación tienen como objetivo encontrar materiales competitivos que puedan mejorar el rendimiento de MCP.

El Laboratorio Nacional Argonne selecciona materiales AZO para la capa conductora ALD-MCP teniendo en cuenta los requisitos de resistencia MCP. Si la resistencia es demasiado alta, la capa conductora no puede reponer electrones a la capa de emisión a tiempo y continuamente, el MCP tendrá ganancias bajas o incluso no funcionará. Por otro lado, si la resistencia es demasiado baja, el MCP se sobrecalentará, lo que eventualmente conducirá a una ruptura [4, 9, 14, 15]. Por lo tanto, el diseño de la capa conductora es importante para un ALD-MCP.

Como se muestra en la Fig. 2, cuando la resistividad de la capa conductora de AZO está dentro del requisito de resistencia MCP, el contenido de Zn permitido está en un rango muy estrecho (70-73%) [16]. Por lo tanto, la ganancia del MCP es inestable y el MCP puede romperse fácilmente. Se han estudiado materiales conductores alternativos como W y Mo en lugar de Zn [3, 4, 17,18,19]. La reacción química de \ ({\ text {WF}} _ {6} \) (\ ({\ text {MoF}} _ {6} \)) y \ ({\ text {H}} _ {2} {\ text {O}} \) se usa para aumentar W (Mo) por ALD. Sin embargo, usar \ ({\ text {WF}} _ {6} \) o \ ({\ text {MoF}} _ {6} \) tiene dos serias desventajas:son fuertemente corrosivos y contienen impurezas que pueden ser Difícil de eliminar durante el proceso de producción. Por estas razones, ALD-MCP con estos materiales es costoso.

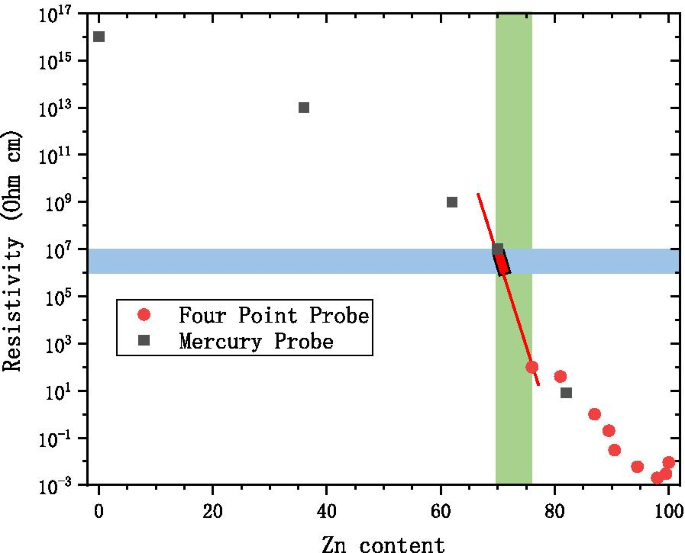
Contenido de Zn, Zn / (Zn + A) * 100 (%), área azul como área de resistencia MCP, área verde como área de cambio AZO, áreas rojas como área de necesidad de control

En nuestro estudio, encontramos que se pueden realizar diseños razonables con ZnO y \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) para la capa conductora MCP, sin los desafíos enfrenta si se utiliza W o Mo, y es más competitivo en precio. Aquí, nombramos el ALD-MCP con una capa conductora AZO como AZO-ALD-MCP.

Proponemos un algoritmo para ajustar la proporción de material conductor ZnO y material de alta resistencia \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) para obtener nuestras características deseadas de capa conductora AZO.

Presentamos el concepto de la resistencia de trabajo del MCP (es decir, la resistencia durante la avalancha de electrones en el microcanal). Probamos la resistencia de trabajo de AZO-ALD-MCP y encontramos dos diferencias entre los AZO-ALD-MCP y los MCP convencionales. Observamos que las resistencias de trabajo y de inactividad de los MCP AZO-ALD-MCP y los MCP convencionales son significativamente diferentes. Además, la resistencia de AZO-ALD-MLP está correlacionada negativamente con el voltaje. Nuestra propuesta (la referencia a la resistencia de trabajo) para ajustar la relación del material conductor y el material de alta resistencia proporciona una guía para ayudarnos a buscar nuevos materiales que se utilizarán para la capa conductora ALD-MCP para mejorar el rendimiento de la capa conductora de ALD-MCP. MCP en el futuro.

Experimental y métodos

ZnO creciente y \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) Película atómica

La deposición de capa atómica (ALD) es una tecnología que alterna precursores y gases reactivos en la superficie del sustrato para la adsorción física o química o la reacción de saturación de la superficie a una velocidad controlada. El material se deposita sobre el sustrato en forma de una superficie de película monoatómica. ALD puede producir una película continua sin poros, con excelente cobertura y puede controlar el espesor y la composición de la película atómica [1, 2, 4, 11, 13, 19, 20].

Las siguientes son las ecuaciones de reacción química del uso de ALD para hacer crecer Al ₂ O ₃ :

$$ \ begin {alineado} &{\ text {A}}:{\ text {Sustrato}} - {\ text {OH}} ^ {*} + {\ text {Al}} \ left ({{\ text {CH}} _ {3}} \ right) _ {3} \\ &\ quad \ to {\ text {Substrate}} - {\ text {O}} - {\ text {Al}} \ left ({ {\ text {CH}} _ {3}} \ right) _ {2} ^ {*} + {\ text {CH}} _ {4} \ uparrow \\ &{\ text {B}}:{\ text {Substrate}} - {\ text {O}} - {\ text {Al}} \ left ({{\ text {CH}} _ {3}} \ right) _ {2} ^ {*} + 2 {\ text {H}} _ {2} {\ text {O}} \\ &\ quad \ to {\ text {Substrate}} - {\ text {O}} - {\ text {Al}} \ left ({{\ text {OH}}} \ right) _ {2} ^ {*} + 2 {\ text {CH}} _ {4} \ uparrow \\ &{\ text {C}}:{\ text {Al}} - {\ text {OH}} ^ {*} + {\ text {Al}} \ left ({{\ text {CH}} _ {3}} \ right) _ {3} \\ { } &\ quad \ to {\ text {Al}} - {\ text {O}} - {\ text {Al}} \ left ({{\ text {CH}} _ {3}} \ right) _ { 2} ^ {*} + {\ text {CH}} _ {4} \ uparrow \\ &{\ text {D}}:{\ text {Al}} - {\ text {CH}} _ {3} ^ {*} + {\ text {H}} _ {2} {\ text {O}} \ to {\ text {Al}} - {\ text {OH}} ^ {*} + 2 {\ text { CH}} _ {4} \ uparrow \\ \ end {alineado} $$

La temperatura de reacción es de 60 a 150 ° C. Como se muestra en la Fig.3, el tiempo y el orden de crecimiento de una capa de Al ₂ O ₃ átomo es:

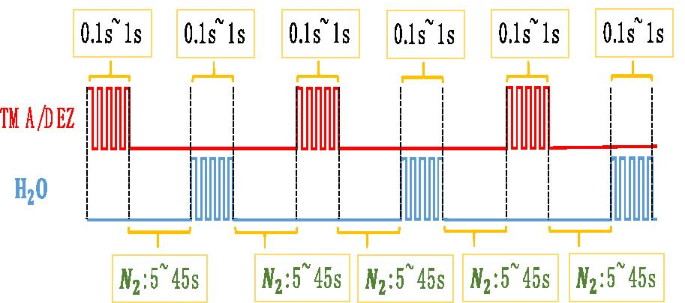
Creciendo Al ₂ O ₃ y diagrama de ZnO

\ ({\ text {TMA}} / {\ text {N}} _ {2} / {\ text {H}} _ {2} {\ text {O}} / {\ text {N}} _ { 2} =0.1 \ sim1 {\ text {s}} / 5 \ sim45 {\ text {s}} / 0.1 \ sim1 {\ text {s}} / 5 \ sim45 {\ text {s}} \).

Las siguientes son las ecuaciones de reacción química para usar ALD para hacer crecer ZnO:

$$ \ begin {alineado} &{\ text {E}}:{\ text {Sustrato}} - {\ text {OH}} ^ {*} + {\ text {Zn}} \ left ({{\ text {CH}} _ {2} {\ text {CH}} _ {3}} \ right) _ {2} \\ &\ quad \ to {\ text {Substrate}} - {\ text {O}} - {\ text {ZnCH}} _ {2} {\ text {CH}} _ {3} ^ {*} + {\ text {CH}} _ {3} {\ text {CH}} _ {3} \ uparrow \\ &{\ text {F}}:{\ text {Sustrato}} - {\ text {O}} - {\ text {ZnCH}} _ {2} {\ text {CH}} _ {3} ^ {*} + {\ text {H}} _ {2} {\ text {O}} \\ &\ quad \ to {\ text {Substrate}} - {\ text {O}} - {\ text { ZnOH}} ^ {*} + {\ text {CH}} _ {3} {\ text {CH}} _ {3} \ uparrow \\ &{\ text {G}}:{\ text {Zn}} - {\ text {OH}} ^ {*} + {\ text {Zn}} \ left ({{\ text {CH}} _ {2} {\ text {CH}} _ {3}} \ right) _ {2} \\ &\ quad \ to {\ text {Zn}} - {\ text {O}} - {\ text {ZnCH}} _ {2} {\ text {CH}} _ {3} ^ {*} + {\ text {CH}} _ {3} {\ text {CH}} _ {3} \ uparrow \\ &{\ text {H}}:{\ text {Zn}} - {\ text {CH}} _ {2} {\ text {CH}} _ {3} ^ {*} + {\ text {H}} _ {2} {\ text {O}} \ to {\ text {Zn} } - {\ text {OH}} ^ {*} + {\ text {CH}} _ {3} {\ text {CH}} _ {3} \ uparrow \\ \ end {alineado} $$

La temperatura de reacción es de 60 a 150 ° C. Como se muestra en la Fig.3, el tiempo y el orden de crecimiento de una capa de átomo de ZnO es:

$$ {\ text {DEZ}} / {\ text {N}} _ {2} / {\ text {H}} _ {2} {\ text {O}} / {\ text {N}} _ { 2} =0.1 \ sim1 {\ text {s}} / 5 \ sim45 {\ text {s}} / 0.1 \ sim1 {\ text {s}} / 5 \ sim45 {\ text {s}} {.} $ PS

Diseño de la capa conductora AZO

El espesor del AZO suele oscilar entre 300 y 1000 capas atómicas. Definimos una nueva regla de operación matemática para diseñar los órdenes de capa atómica de Al2O3 y ZnO con el fin de ajustar la relación del material conductor ZnO y el material de alta resistencia Al2O3.

$$ \ left (\ begin {array} {* {20} c} {{\ text {mA}}} \\ {{\ text {mB}}} \\ \ vdots \\ \ end {array} \ right ) ={\ text {m}} \ left (\ begin {array} {* {20} c} {\ text {A}} \\ {\ text {B}} \\ \ vdots \\ \ end {array } \ right) $$ (1) $$ \ begin {alineado} &{\ text {A}} \ left (\ begin {array} {* {20} c} {\ text {a}} \\ {\ texto {b}} \\ \ vdots \\ \ end {matriz} \ right) + {\ text {B}} \ left (\ begin {array} {* {20} c} {\ text {c}} \ \ {\ text {d}} \\ \ vdots \\ \ end {matriz} \ right) + {\ text {C}} \ left (\ begin {array} {* {20} c} {\ text {e }} \\ {\ text {f}} \\ \ vdots \\ \ end {matriz} \ derecha) \ ldots \\ &\ quad =\ left (\ begin {matriz} {* {20} c} {\ texto {A}} \\ {\ text {B}} \\ \ vdots \\ \ end {matriz} \ right) \ left [\ left (\ begin {array} {* {20} c} {\ text { a}} \\ {\ text {b}} \\ \ vdots \\ \ end {matriz} \ derecha) \ izquierda (\ begin {matriz} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ vdots \\ \ end {matriz} \ right) \ left (\ begin {matriz} {* {20} c} {\ text {e}} \\ {\ text {f }} \\ \ vdots \\ \ end {matriz} \ right) \ ldots \ right] =\ left (\ begin {matriz} {* {20} c} {{\ text {Aa}} + {\ text { Bc}} + {\ text {Ce}} + \ ldots} \\ {{\ text {Ab}} + {\ text {Bd}} + {\ text {Cf}} + \ ldots} \\ \ vdots \\ \ end {matriz} \ right) \\ \ end {alineado} $$ (2)

La operación matemática se denominó operación WYM. La operación WYM tiene dos propiedades y una fórmula.

Propiedad 1 de WYM:

$$ \ begin {alineado} &\ left ({\ begin {array} {* {20} c} {\ text {m}} \\ {\ text {n}} \\ \ end {array}} \ right ) \ left [{\ left ({\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {array}} \ right) \ left ({\ begin {array} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {array}} \ right)} \ right] \ left [{\ left ({\ begin {array} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {array}} \ right) \ left ({\ begin {array } {* {20} c} {\ text {g}} \\ {\ text {h}} \\ \ end {matriz}} \ right)} \ right] \ left [{\ left ({\ begin { matriz} {* {20} c} {\ text {i}} \\ {\ text {j}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {k}} \\ {\ text {l}} \\ \ end {matriz}} \ derecha)} \ derecha] \ ldots \\ &\ quad =\ left ({\ begin {matriz} {* {20} c} {\ text {m}} \\ {\ text {n}} \\ \ end {matriz}} \ derecha) \ left \ {{\ left ({\ begin {matriz} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {g }} \\ {\ text {h}} \\ \ end {matriz}} \ right)} \ right], \ left ({\ beg en {matriz} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz } {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c } {\ text {g}} \\ {\ text {h}} \\ \ end {matriz}} \ derecha)} \ derecha]} \ derecha \} \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} {\ text {i}} \\ {\ text {j}} \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} {\ text {k}} \\ {\ text {l}} \\ \ end {matriz}} \ derecha)} \ derecha] \ ldots \\ &\ quad =\ left ({\ begin {matriz} {* {20} c} {\ text {m}} \\ {\ text {n}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {c }} \\ {\ text {d}} \\ \ end {matriz}} \ right)} \ right] \ left \ {{\ left ({\ begin {matriz} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {i} } \\ {\ text {j}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {k}} \\ {\ text { l}} \\ \ end {matriz}} \ derecha)} \ derecha], \ izquierda ({\ begin {matriz} {* {20} c} {\ te xt {g}} \\ {\ text {h}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {i }} \\ {\ text {j}} \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {k}} \\ {\ text {l}} \\ \ end {matriz}} \ derecha)} \ derecha]} \ derecha \} \ ldots \\ \ end {alineado} $$

Propiedad 2 de WYM:

$$ \ begin {alineado} &{\ text {A}} \ left ({\ begin {array} {* {20} c} {\ text {m}} \\ {\ text {n}} \\ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {matriz }} \ right) \ left ({\ begin {array} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {array}} \ right)} \ derecha] \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {array} {* {20} c} {\ text {g}} \\ {\ text {h}} \\ \ end {array}} \ right)} \ right] \ ldots \\ &\ quad =\ left ({\ begin {array} {* {20} c} {{\ text {Am}}} \\ {{\ text {An}}} \\ \ end {array}} \ right ) \ left [{\ left ({\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {array}} \ right) \ left ({\ begin {array} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {array}} \ right)} \ right] \ left [{\ left ({\ begin {array} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {array}} \ right) \ left ({\ begin {array } {* {20} c} {\ text {g}} \\ {\ text {h}} \\ \ end {matriz}} \ right)} \ right] \ ldots \\ &\ quad =\ left ( {\ begin {array} {* {20} c} {\ text {m}} \\ {\ text {n}} \\ \ end {a rray}} \ right) \ left [{{\ text {A}} \ left ({\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {b}} \ \ \ end {matriz}} \ right), {\ text {A}} \ left ({\ begin {matriz} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {matriz}} \ right)} \ right] \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {e}} \\ {\ text {f} } \\ \ end {matriz}} \ right) \ left ({\ begin {matriz} {* {20} c} {\ text {g}} \\ {\ text {h}} \\ \ end {matriz }} \ right)} \ right] \ ldots \\ &\ quad =\ left ({\ begin {array} {* {20} c} {\ text {m}} \\ {\ text {n}} \ \ \ end {matriz}} \ right) \ left [{\ left ({\ begin {matriz} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} {\ text {c}} \\ {\ text {d}} \\ \ end {matriz}} \ derecha) } \ right] \ left [{{\ text {A}} \ left ({\ begin {array} {* {20} c} {\ text {e}} \\ {\ text {f}} \\ \ end {array}} \ right), {\ text {A}} \ left ({\ begin {array} {* {20} c} {\ text {g}} \\ {\ text {h}} \\ \ end {matriz}} \ derecha)} \ derecha] \ ldots \\ \ end {alineado} $$

Fórmula WYM:

$$ \ begin {alineado} &\ left (\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ vdots \\ \ end {array} \ right) =\ left (\ begin {array} {* {20} c} {{\ text {A}} + \ frac {{\ text {X}}} {{\ text {Y}}}} \ \ {\ text {b}} \\ \ vdots \\ \ end {matriz} \ right) \ propto {\ text {Y}} \ left (\ begin {matriz} {* {20} c} {{\ text {A}} + \ frac {{\ text {X}}} {{\ text {Y}}}} \\ {\ text {b}} \\ \ vdots \\ \ end {matriz} \ right) =\ left ({\ begin {array} {* {20} c} {{\ text {Y}} - {\ text {X}}} \\ {\ text {X}} \\ \ end {array}} \ right) \ left [\ left (\ begin {array} {* {20} c} {\ text {A}} \\ {\ text {b}} \\ \ vdots \\ \ end {array} \ right ) \ left (\ begin {array} {* {20} c} {{\ text {A}} + 1} \\ {\ text {b}} \\ \ vdots \\ \ end {array} \ right) \ right] \\ &\ left (\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {b}} \\ \ vdots \\ \ end {array} \ right ) =\ left (\ begin {array} {* {20} c} {\ text {a}} \\ {{\ text {B}} + \ frac {{\ text {X}}} {{\ text {Y}}}} \\ \ vdots \\ \ end {matriz} \ right) \ propto {\ text {Y}} \ left (\ begin {matriz} {* {20} c} {\ text {a} } \\ {{\ text {B}} + \ frac {{\ text {X}}} {{\ text {Y}}}} \\ \ vdots \\ \ end {array} \ right) =\ left ({\ begin {array} {* {20} c} {{\ text {Y}} - {\ text {X}}} \\ {\ text {X}} \\ \ end {array}} \ right) \ left [\ left (\ begin {array} {* {20} c} {\ text {a}} \\ {\ text {B}} \\ \ vdots \\ \ end {array} \ right ) \ left (\ begin {array} {* {20} c} {\ text {a}} \\ {{\ text {B}} + 1} \\ \ vdots \\ \ end {array} \ right) \ right] \\ \ end {alineado} $$

Tenga en cuenta que las letras minúsculas representan números reales, mientras que las letras mayúsculas representan números enteros. En los Ejemplos 1 y 2, mostramos una ejecución de la operación.

Ejemplo 1

$$ \ left ({\ begin {array} {* {20} c} {{\ text {ZnO}}} \\ {{\ text {Al}} _ {2} {\ text {O}} _ { 3}} \\ \ end {matriz}} \ right) =\ left ({\ begin {matriz} {* {20} c} {4 + \ frac {1} {2}} \\ 1 \\ \ end {matriz}} \ derecha) \ propto \ left ({\ begin {matriz} {* {20} c} 1 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end { matriz}} \ derecha)} \ derecha] =\ izquierda ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) + \ izquierda ({\ begin { matriz} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ derecha) $$

La operación se interpreta como si tuviera dos esquemas:\ (\ left ({\ begin {array} {* {20} c} 4 \\ 1 \\ \ end {array}} \ right) \) y \ (\ left ( {\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ derecha) \). Para el primer esquema, haga crecer 4 veces la capa atómica de ZnO y una capa atómica de Al2O3. Para el segundo esquema, haga crecer 5 veces la capa atómica de ZnO y una capa atómica de Al2O3. Si repetimos estos dos esquemas dos veces, obtendremos la estructura que se muestra en la Fig. 4.

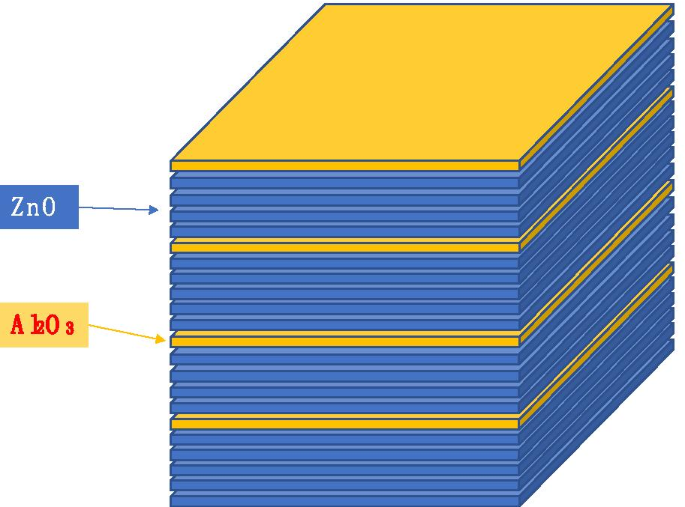
Diagrama esquemático de ZnO y Al ₂ O ₃ secuencia de crecimiento

En el Ejemplo 2 se muestra un uso más complicado de las reglas de operación, como sigue:

$$ \ begin {alineado} &\ left ({\ begin {array} {* {20} c} {{\ text {ZnO}}} \\ {{\ text {Al}} _ {2} {\ text {O}} _ {3}} \\ \ end {matriz}} \ right) =\ left ({\ begin {matriz} {* {20} c} {4.71} \\ 1 \\ \ end {matriz} } \ right) =\ left ({\ begin {array} {* {20} c} {4 + 0.71} \\ 1 \\ \ end {array}} \ right) \\ &\ frac {2} {3 } =0,666 <0,71 <\ frac {3} {4} =0,75 \\ &\ left ({\ begin {array} {* {20} c} E \\ F \\ \ end {array}} \ right) \ left [{\ left ({\ begin {array} {* {20} c} {4 + \ frac {2} {3}} \\ 1 \\ \ end {array}} \ right) \ left ({ \ begin {array} {* {20} c} {4 + \ frac {3} {4}} \\ 1 \\ \ end {array}} \ right)} \ right] \\ &\ quad =E \ izquierda ({\ begin {matriz} {* {20} c} {4 + \ frac {2} {3}} \\ 1 \\ \ end {matriz}} \ derecha) + F \ izquierda ({\ begin { matriz} {* {20} c} {4 + \ frac {3} {4}} \\ 1 \\ \ end {matriz}} \ right) =\ left ({\ begin {matriz} {* {20} c} {4E + 4F + \ frac {2} {3} E + \ frac {3} {4} F} \\ {E + F} \\ \ end {matriz}} \ right) \\ &\ quad =E + F \ left ({\ begin {array} {* {20} c} {4 + \ frac {{\ frac {2} {3} E + \ frac {3} {4} F}} {E + F}} \\ 1 \\ \ end {matriz}} \ derecha) \ propto \ izquierda ({\ begin {matriz} {* {20} c} {4 + \ frac {{\ frac {2} {3} E + \ frac {3} {4} F}} {E + F}} \\ 1 \\ \ end {matriz}} \ right) =\ left ({\ begin {array} {* {20} c} {4.71} \\ 1 \\ \ end {array}} \ right) \\ &\ frac {{\ frac {2} { 3} E + \ frac {3} {4} F}} {E + F} =0,71 \ Flecha derecha {\ text {E}} =12, {\ text {F}} =13 \\ &\ left ({ \ begin {array} {* {20} c} E \\ F \\ \ end {array}} \ right) =\ left ({\ begin {array} {* {20} c} {12} \\ { 13} \\ \ end {matriz}} \ right) =12 \ left ({\ begin {matriz} {* {20} c} 1 \\ {1 \ frac {1} {12}} \\ \ end { matriz}} \ derecha) =\ izquierda ({\ begin {matriz} {* {20} c} {11} \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} 1 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 1 \\ 2 \\ \ end { array}} \ right)} \ right] \\ &\ left ({\ begin {array} {* {20} c} E \\ F \\ \ end {array}} \ right) \ left [{\ left ({\ begin {array} {* {20} c} {4 + \ frac {2} {3}} \\ 1 \\ \ end {array}} \ right), \ left ({\ begin {array} {* {20} c} {4 + \ frac {3} {4}} \\ 1 \\ \ end {matriz}} \ right)} \ right] \\ &\ quad =\ left ({\ begin { array} {* {20} c} E \\ F \\ \ end {array}} \ right) \ left [{ \ left ({\ begin {array} {* {20} c} 1 \\ 2 \\ \ end {array}} \ right) \ left [{\ left ({\ begin {array} {* {20} c } 4 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ derecha)} \ derecha ], \ left ({\ begin {array} {* {20} c} 1 \\ 3 \\ \ end {array}} \ right) \ left [{\ left ({\ begin {array} {* {20 } c} 4 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ derecha)} \ right]} \ right] \\ &\ left ({\ begin {array} {* {20} c} {4.71} \\ 1 \\ \ end {array}} \ right) \ propto \ left ({\ begin {array} {* {20} c} {12} \\ {13} \\ \ end {array}} \ right) \ left [{\ left ({\ begin {array} {* {20} c} 1 \\ 2 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 1 \\ 3 \\ \ end {matriz}} \ derecha)} \ derecha] \ left [{\ left ({\ begin {array} {* {20} c} 4 \\ 1 \\ \ end {array}} \ right) \ left ({\ begin {array} {* {20} c } 5 \\ 1 \\ \ end {matriz}} \ derecha)} \ derecha] =\ izquierda ({\ begin {matriz} {* {20} c} {11} \\ 1 \\ \ end {matriz} } \ right) \ left [{\ left ({\ begin {array} {* {20} c} 1 \\ 1 \\ \ end {array}} \ right) \ left ({\ begin {array} {* {20} c } 1 \\ 2 \\ \ end {matriz}} \ right)} \ right] \ left [{\ left ({\ begin {matriz} {* {20} c} 1 \\ 2 \\ \ end {matriz }} \ right) \ left ({\ begin {array} {* {20} c} 1 \\ 3 \\ \ end {array}} \ right)} \ right] \ left [{\ left ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) \ izquierda ({\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end { array}} \ right)} \ right] \\ \ end {alineado} $$

Plan 1 :\ (\ left ({\ begin {array} {* {20} c} {4.71} \\ 1 \\ \ end {array}} \ right) \ propto 12 \ left [{\ left ({\ begin { matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) + 2 \ izquierda ({\ begin {matriz} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ derecha)} \ derecha] + 13 \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) + 3 \ left ({\ begin {array} {* {20} c} 5 \\ 1 \\ \ end {array}} \ right)} \ right] \).

Plan 2 \ (\ left ({\ begin {array} {* {20} c} {4.71} \\ 1 \\ \ end {array}} \ right) \ propto 11 \ left [{\ left [{\ left ({ \ begin {array} {* {20} c} 4 \\ 1 \\ \ end {array}} \ right) + 2 \ left ({\ begin {array} {* {20} c} 5 \\ 1 \ \ \ end {matriz}} \ derecha)} \ derecha] + \ izquierda [{\ izquierda ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz}} \ derecha) + 3 \ left ({\ begin {array} {* {20} c} 5 \\ 1 \\ \ end {array}} \ right)} \ right]} \ right] + \ left [{\ left [{ \ left ({\ begin {array} {* {20} c} 4 \\ 1 \\ \ end {array}} \ right) + 2 \ left ({\ begin {array} {* {20} c} 5 \\ 1 \\ \ end {matriz}} \ right)} \ right] + 2 \ left [{\ left ({\ begin {matriz} {* {20} c} 4 \\ 1 \\ \ end {matriz }} \ right) + 3 \ left ({\ begin {array} {* {20} c} 5 \\ 1 \\ \ end {array}} \ right)} \ right]} \ right] \).

En el Ejemplo 2, la operación en el Plan 1 se puede interpretar de la siguiente manera:

Esquema 1 ALD crece 4 veces el proceso de crecimiento de la capa atómica de ZnO y un \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) proceso de crecimiento de la capa atómica; ALD crece 5 veces el proceso de crecimiento de la capa atómica de ZnO y un proceso de crecimiento de la capa atómica \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \), y se repite dos veces.

Esquema 2 ALD crece 4 veces el proceso de crecimiento de la capa atómica de ZnO y un \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) proceso de crecimiento de la capa atómica; ALD crece 5 veces el proceso de crecimiento de la capa atómica de ZnO y un proceso de crecimiento de la capa atómica \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \), y se repite tres veces.

Repita el esquema 1 12 veces y el esquema 2 13 veces.

La interpretación de la operación en el Plan 2 está en la misma línea que el Plan 1.

Prueba de resistencia de placa de microcanal

Como se muestra en la Fig. 5a, usamos tecnología de deposición de capa atómica para hacer crecer la capa conductora AZO y la capa de emisión \ ({\ text {Al}} _ {2} {\ text {O}} _ {3} \) en paredes de microcanales de las matrices de poros bidimensionales. Y luego usamos tecnología de evaporación térmica para hacer crecer la capa del electrodo de Ni-Cr en ambos lados del MCP [2, 4] y colocar el anillo del electrodo en ambos lados del MCP. Haciendo los preparativos para lo anterior, probamos directamente la resistencia ALD-MCP. En esta condición, definimos la resistencia MCP correspondiente como la resistencia de inactividad del MCP. Usamos un electrómetro Keithley modelo 6517B para medir la resistencia de inactividad del MCP en un 10 ⁻³ –10 ⁻⁵ Pa vacío [1, 4, 13].

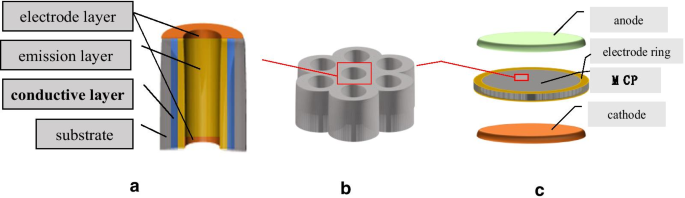
Diagrama esquemático de la prueba de resistencia ALD – MCP

Como se muestra en la Fig. 5c, usamos un cañón de electrones como cátodo y una pantalla de fósforo como ánodo. El cañón de electrones proporciona electrones incidentes al MCP y la pantalla de fósforo recibe los electrones emitidos por el MCP. Además, cuando el MCP está en funcionamiento, la pantalla de fósforo de alto voltaje emitirá luz verde para detectar la uniformidad del MCP [1, 21].

Como se muestra en la Fig. 1, usamos un cañón de electrones que proporciona 100 pA como entrada del MCP para medir la corriente. Debido a un número creciente de electrones secundarios, habrá una condición en la que la capa de emisión pierde una gran cantidad de cargas y la capa conductora proporciona continuamente una corriente de cargas a la capa de emisión. En esta condición, definimos la resistencia MCP correspondiente como la resistencia de trabajo del MCP. El entorno de vacío de la resistencia de trabajo es 10 ⁻³ –10 ⁻⁵ Pa.

Resultado y discusión

La imagen SEM de la sección transversal de la muestra de AZO-ALD-MCP se muestra en la Fig. 6. Diseñamos una serie de capas conductoras de AZO como se muestra en la Tabla 1 y sus correspondientes resistencias de trabajo y no trabajo en la Fig. 7. En el En la misma figura, también mostramos las resistencias de trabajo y no trabajo de un MCP convencional. En comparación con la resistencia de trabajo de AZO-ALD-MCP, la resistencia de trabajo de AZO-ALD-MCP se reduce significativamente. Sin embargo, no existe una diferencia significativa entre la resistencia de trabajo y la resistencia de inactividad de un MCP convencional. A medida que aumenta el voltaje, la resistencia de trabajo de AZO-ALD-MCP es significativamente menor que la de un MCP convencional. Bajo la misma condición de voltaje, las resistencias de trabajo y de inactividad del AZO-ALD-MCP son estables. Creemos que hay dos razones principales para las características antes mencionadas.

Imagen SEM transversal del AZO-ALD-MCP

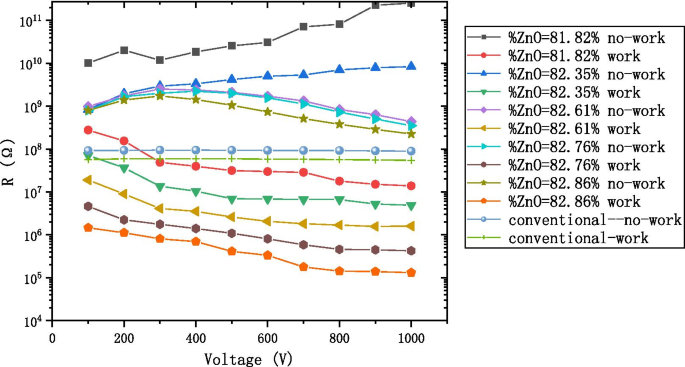
La resistencia de trabajo y la resistencia de no trabajo con el diagrama de voltaje en el AZO-ALD-MCP en la relación diferente y convencional-MCP

Según la fórmula [21],

$$ R _ {{{\ text {MCP}}}} =R_ {0} \ exp \ left [{- \ beta_ {T} \ left ({T _ {{{\ text {MCP}}}} - T_ { 0}} \ right)} \ right] $$

en comparación con el vidrio de plomo, el AZO es un material con un coeficiente de temperatura negativo (NTC) más alto, por lo que la resistencia será menor a la misma temperatura y resistencia inicial. En el proceso de generar ganancia, AZO es bombardeado por electrones incidentes a alto voltaje, generando así más pares de electrones y huecos, lo que resulta en un aumento de la corriente.

Definimos la relación entre la resistencia de inactividad y la resistencia de trabajo para describir la estabilidad de la resistencia del material:

$$ \ kappa_ {R} =\ frac {{R_ {n}}} {{R_ {w}}} $$

La Figura 8 muestra que \ (\ kappa_ {R} \) de AZO-ALD-MCP es aproximadamente 10 ² –10 ³ veces, y el \ (\ kappa_ {R} \) del MCP convencional es aproximadamente 2-3 veces. Esto muestra que el cambio de resistencia de AZO-ALD-MCP es más obvio; por lo tanto, el antiguo concepto de resistencia no funcional como la definición de resistencia MCP debería sustituirse por la resistencia funcional.

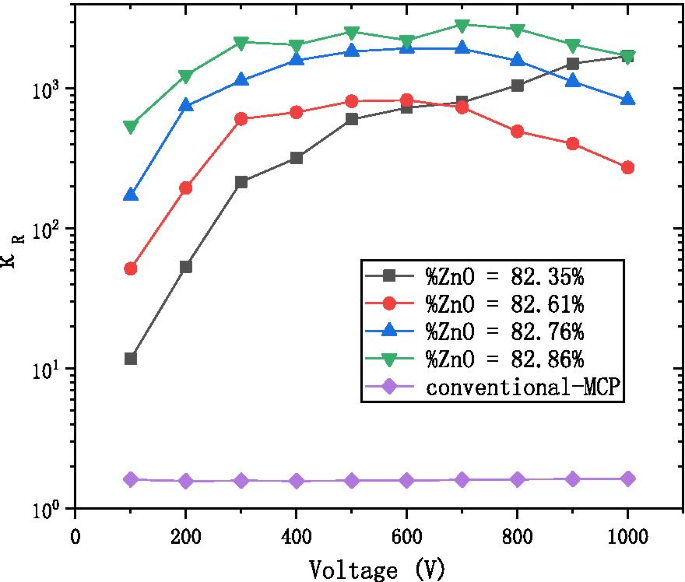
El K _R con el diagrama de voltaje en la diferente relación de AZO-ALD-MCP

La Figura 9 muestra la relación \ (L_ {R} \) de la resistencia del diseño de material "adyacente" con respecto al voltaje de operación. La relación \ (L_ {R} \) se define como:

$$L_{R} =\frac{{R\left( {4 + \frac{N - 1}{N}} \right)}}{{R\left( {4 + \frac{N}{N + 1}} \right)}}$$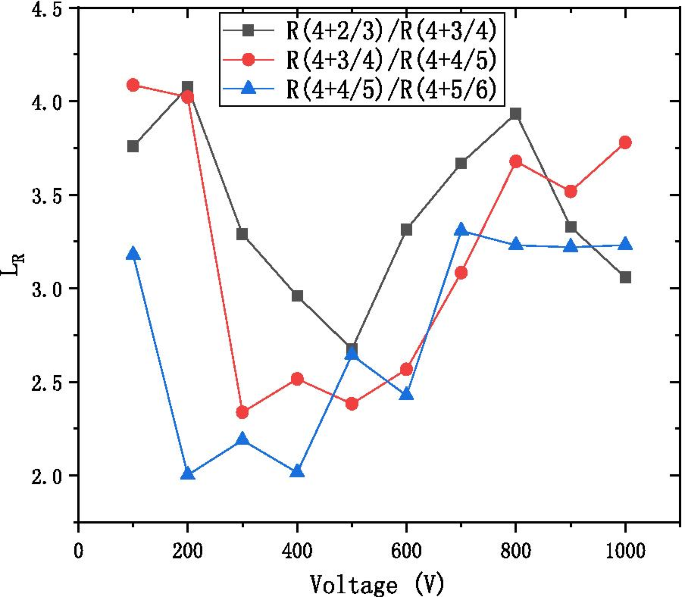

The resistance of the step length L_R with the voltage diagram at the different ratio of the working resistance of neighbor formula

donde

$$\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text{O}}_{3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + \frac{N - 1}{N}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} 1 \\ {N - 1} \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]$$

y

$$\left( {\begin{array}{*{20}c} {{\text{ZnO}}} \\ {{\text{Al}}_{2} {\text{O}}_{3} } \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} {4 + \frac{N}{N + 1}} \\ 1 \\ \end{array} } \right) =\left( {\begin{array}{*{20}c} 1 \\ N \\ \end{array} } \right)\left[ {\left( {\begin{array}{*{20}c} 4 \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 5 \\ 1 \\ \end{array} } \right)} \right]$$

As can be observed from Fig. 9, the L_R value ranges from 2 to 4.5 to adjust ratio of conductive material ZnO and high resistance material \({\text{Al}}_{2} {\text{O}}_{3}\). And it proves the feasibility of WYM operation to design laminated materials.

Figure 10 shows the working resistance with respect to the percentage of ZnO cycles (%ZnO), where %ZnO is defined to be:

$${\text{\% ZnO}} =\frac{{{\text{ZnO}}}}{{{\text{ZnO}} + {\text{Al}}_{2} {\text{O}}_{3} }}{*}100\left( {\text{\% }} \right)$$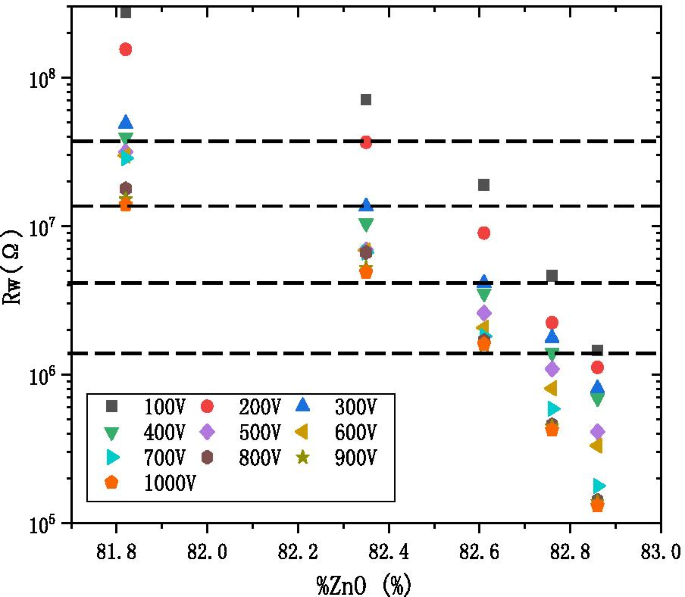

The working resistance with the percentage of ZnO cycles diagram at the different voltage

under various voltage conditions, ranging from 100 to 1000 V. It decreases that the working resistance under the same voltage with the increase in the percentage of ZnO cycles. It can be the same that the working resistance under different the percentage of ZnO cycles and under the different condition of voltage. Therefore, the AZO-ALD-MCP of different formulations works under its specific voltage to meet the MCP resistance index.

We define the ratio of the resistance difference under the different condition of voltage and the voltage difference to describe the effect of the voltage on the resistance of MCP:

$$r =\left| {\frac{{R_{U} - R_{V} }}{U - V}} \right| =\left| {\frac{{R_{1000v} - R_{100v} }}{1000 - 100}} \right|$$

Figure 11 shows that the effect of the voltage on the resistance of AZO-ALD-MCP decreased and gradually stabilized with the increase in the percentage of ZnO cycles. Therefore, the preparation of AZO-ALD-MCP should try to choose a formula with a large percentage of ZnO cycles.

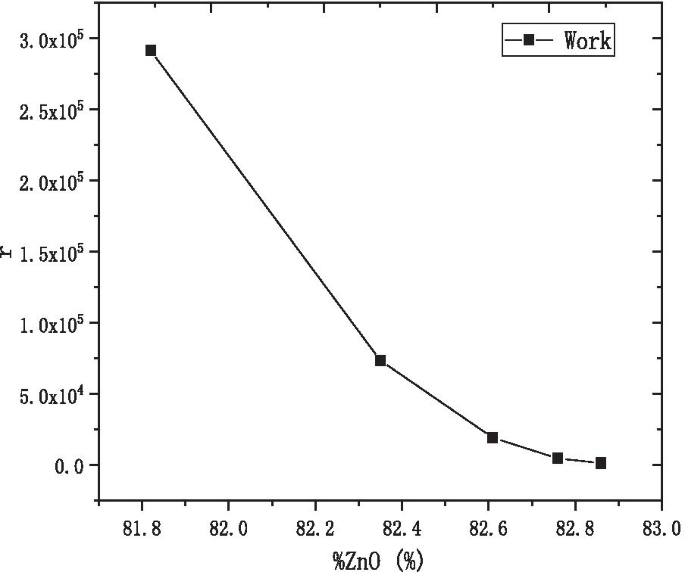
The r with the percentage of ZnO cycles diagram at the working state

Based on the above analysis, we have put forward the reference to the working resistance for the conductive layer of ALD-MCP. As shown in Fig. 5a, we design the AZO conductive layer of AZO-MCP by using the WYM operation and temperature adjustment based on the working resistance. We use atomic layer deposition technology to grow the \({\text{Al}}_{2} {\text{O}}_{3}\) emission layer on microchannel wall of the two-dimensional pore arrays [3, 11, 22]. In Fig. 12a, the gain from our AZO-ALD-MCP is compared to that of a conventional MCP under different voltages. As can be observed, our preparation method of the AZO-ALD-MCP provides a larger gain than that of a conventional MCP. Figure 12b shows the phosphor screen with uniform green light under high pressure, thus proving the uniformity of the material deposited on the wall of each microchannel and the uniformity of the AZO-ALD-MCP field of view.

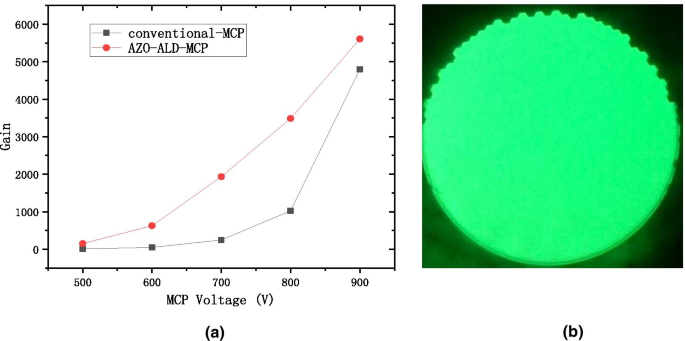
The gain with the voltage diagram at the AZO-ALD-MCP and conventional-MCP

Conclusión

We defined the working and non-working resistance of the microchannel plate. Aiming at the required resistivity of the microchannel plate in the region with extremely narrow zinc content requirement (70–73%), an algorithm for growing the AZO conductive layer is proposed. Compared with the conventional MCP, we found a large difference between the working and non-working resistance and there is also a huge difference under different voltages. Therefore, we analyze the data by defining \(\kappa_{R} ,L_{R} ,\% {\text{ZnO}},r\). MCP should try to choose a formula with a large percentage of ZnO cycles. We recommend using the working resistance as an ALD-MCP resistance indicator in industrial production. Building on our results as described in this work, our studies will help to find even better materials as the conductive layer for the ALD-MCP.

Historial de cambios

Nanoestructuras de MgO dopadas con óxido de grafeno para una degradación del tinte y una acción bactericida altamente eficientes Efecto antibacteriano dual de nanofibras compuestas de curcumina electrohiladas in situ para esterilizar bacterias resistentes a los fármacos