Efectos de interacción en el ensamblaje de nanopartículas magnéticas

Simulación numérica

Nanopartículas que no interactúan

Es instructivo recordar primero el comportamiento de un conjunto de nanopartículas superparamagnéticas que no interactúan en un campo magnético alterno. Permite ver claramente la influencia de la interacción magneto-dipolo en las propiedades del ensamblaje. Basado en la ecuación de Fokker-Planck derivada por W.F. Brown [39], se puede obtener una ecuación cinética aproximada [10] para los números de población n ₁ ( t ) y n ₂ ( t ) de dos pozos potenciales de nanopartículas superparamagnéticas uniaxiales

Aquí, τ ₁ ( T ) y τ ₂ ( T ) son los tiempos de relajación correspondientes a una temperatura determinada T para el primer y segundo pozos potenciales, respectivamente. Los tiempos de relajación τ ₁ ( T ) y τ ₂ ( T ) dependen esencialmente de la amplitud y dirección del campo magnético aplicado con respecto al eje de anisotropía fácil de las partículas (véase el apéndice en la Ref. [10]). El procedimiento de iteración se puede utilizar para calcular los números de población de pozos n ₁ ( t ) y n ₂ ( t ) durante varios períodos del campo magnético alterno. Es suficiente obtener un bucle de histéresis estacionario de una partícula en un campo magnético alterno. Para hacerlo, se puede usar una relación aproximada para el componente de la magnetización de partículas reducida a lo largo de la dirección del campo magnético

Aquí, θ ₀ es el ángulo del campo magnético externo con respecto al eje de anisotropía fácil de la partícula, θ _{min, 1} y θ _{min, 2} son las ubicaciones de los mínimos del pozo potencial como las funciones del campo magnético aplicado reducido, h _e ( t ) = H ₀ pecado ( ωt ) / H _a , donde ω =2π f es la frecuencia angular, H _a siendo el campo de anisotropía de partículas. Para obtener un bucle de histéresis de un conjunto de nanopartículas independientes orientadas aleatoriamente, es necesario promediar la magnetización reducida m _h ( t ) sobre las direcciones del campo magnético. Vale la pena señalar que la precisión de una solución analítica aproximada, Eq. (1), (2), de la ecuación de Fokker-Planck ha sido validado [10] mediante comparación directa con las soluciones numéricas de la ecuación estocástica de Landau-Lifshitz para nanopartículas magnéticas no interactuantes.

Clústeres de nanopartículas

Para investigar el efecto de la interacción magneto-dipolo sobre la tasa de absorción específica de un ensamblaje de nanopartículas magnéticas que interactúan en un campo magnético alterno, en este artículo estudiamos el comportamiento de un ensamblaje diluido de clusters 3D habituales de nanopartículas superparamagnéticas y el de fractal agrupaciones [8, 9] que surgen normalmente en medios biológicos cargados con nanopartículas magnéticas finas.

Un grupo 3D cuasi esférico de nanopartículas que se muestra esquemáticamente en la Fig. 1a se puede caracterizar por su radio R _cl y el número de nanopartículas, N _p >> 1, dentro de su volumen. Se supone que las nanopartículas tienen casi el mismo diámetro D , y sus centros, { r _i }, i =1, 2, .. N _p , se distribuyen aleatoriamente en el volumen del clúster. También asumimos que las partículas están recubiertas con delgadas capas no magnéticas, por lo que la interacción de intercambio entre las nanopartículas vecinas del cúmulo está ausente. Como mencionamos anteriormente, dicho clúster 3D se caracteriza por la densidad de empaquetamiento de nanopartículas η = N _p V / V _cl . Este es un volumen total del material magnético distribuido en el volumen del cúmulo. Se puede definir la distancia media entre las nanopartículas del cúmulo mediante la relación D _av =(6 V _cl / πN _p ) ^1/3 . Luego, la densidad de empaquetamiento de nanopartículas viene dada por η =( D / D _av ) ³ .

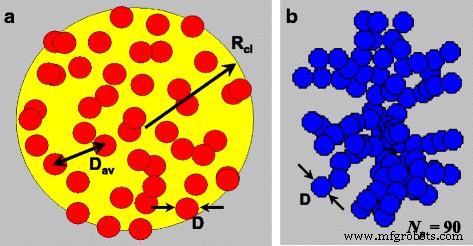
Geometría de un grupo 3D aleatorio cuasi esférico de nanopartículas de dominio único ( a ) y grupo fractal ( b ) con descriptores fractales D _f =2.1 y k _f =1.3

Para un ensamblaje de clústeres 3D completamente aleatorios, las orientaciones de los ejes de anisotropía fáciles de nanopartículas { e _i }, i =1, 2, .. N _p , se eligen aleatoria e independientemente en la esfera de la unidad. Alternativamente, se puede suponer que durante la formación de grupos en una solución bajo la influencia de la interacción magneto-estática, se produce cierta correlación en la distribución de las direcciones del eje de anisotropía fácil de las nanopartículas. Una posibilidad para describir estos grupos parcialmente ordenados es asumir que los ejes fáciles de anisotropía de las nanopartículas se distribuyen uniformemente en un ángulo sólido, θ < θ _max , en las coordenadas esféricas.

Cúmulos 3D aleatorios con un número determinado de partículas N _p de diámetro D se crearon en este estudio de la siguiente manera. Primero, generamos un conjunto suficientemente denso y aproximadamente uniforme de N puntos aleatorios { ρ _i } dentro de un volumen esférico del radio R _cl , de modo que | ρ _i | ≤ R _cl para todos los puntos generados, i =1, 2 ... N , N >> N _p . El centro de la primera nanopartícula se colocó en el primer punto aleatorio, r ₁ = ρ ₁ . Luego, todos los puntos aleatorios con coordenadas | ρ _i - r ₁ | ≤ D se eliminaron del conjunto inicial de puntos aleatorios. Después de esta operación, cualquier punto del conjunto restante de puntos aleatorios podría usarse como centro de la segunda nanopartícula. Por ejemplo, se puede poner simplemente r ₂ = ρ ₂ . En el siguiente paso, se eliminan todos los puntos aleatorios cuyas coordenadas satisfacen la desigualdad | ρ _i - r ₂ | ≤ D . Este procedimiento se repite hasta que todos N _p Los centros de nanopartículas se colocan dentro del volumen del grupo. Como resultado, todos los centros de nanopartículas aleatorios se encuentran dentro de una esfera de radio R _cl , de modo que | r _i | ≤ R _cl , yo =1, 2, ... N _p . Además, ninguna de las nanopartículas está en contacto directo con las nanopartículas vecinas. Este algoritmo permite construir agrupaciones 3D cuasi esféricas aleatorias de nanopartículas magnéticas para valores moderados de la fracción de volumen de nanopartículas η <0.5.

Para un conjunto dado de parámetros iniciales, es decir, D , R _cl y N _p , varios clústeres 3D aleatorios se diferencian por los conjuntos de coordenadas de los centros de nanopartículas { r _i } y orientaciones { e _i } de los ejes de anisotropía fácil de partículas. Sin embargo, los cálculos muestran que en el límite N _p >> 1, los bucles de histéresis obtenidos para diferentes realizaciones de variables aleatorias { r _i } y { e _i } difieren sólo ligeramente entre sí. Para caracterizar el comportamiento de un ensamblaje diluido de grupos de nanopartículas aleatorios, es necesario calcular el ciclo de histéresis del ensamblaje promediado sobre un número suficientemente grande de realizaciones de grupos aleatorios. Se encuentra que en el límite N _p >> 1, el ciclo de histéresis promedio del ensamblaje del clúster tiene una dispersión bastante pequeña, incluso siendo promediado sobre 20-30 realizaciones independientes de clústeres aleatorios con los valores fijos de los parámetros iniciales D , R _cl y N _p .

La geometría de los grupos fractales de nanopartículas de dominio único se caracteriza [42, 43] por los descriptores fractales D _f y k _f . Por definición, el número total de nanopartículas N _p en el grupo fractal viene dado por la relación \ ({N} _p ={k} _f {\ left (2 {R} _g / D \ right)} ^ {D_f} \), donde D _f es la dimensión fractal, k _f es el prefactor fractal, y R _g siendo el radio de giro. Se define [43] mediante el cuadrado medio de las distancias entre los centros de partículas y el centro geométrico de masa del agregado. En este artículo, los grupos fractales con varios descriptores fractales se crearon utilizando el conocido algoritmo de Filippov et al. [43]. Como ejemplo, la Fig. 1b muestra la estructura geométrica del racimo fractal con descriptores fractales D _f =2.1 y k _f =1.3 que consta de N _p =90 nanopartículas de dominio único. Geométricamente, parece que la principal diferencia entre 3D y clústeres fractales es que en el último caso, cada nanopartícula tiene al menos un vecino ubicado a la distancia más cercana posible entre los centros de nanopartículas igual al diámetro de la nanopartícula D .

Dinámica del vector de magnetización unitaria \ ({\ overrightarrow {\ alpha}} _ i \) de i La -ésima nanopartícula de dominio único del cúmulo está determinada por la ecuación estocástica de Landau-Lifshitz (LL)

donde γ es la relación giromagnética, κ es el parámetro de amortiguamiento fenomenológico, γ ₁ = γ / (1+ κ ² ), \ ({\ overrightarrow {H}} _ {ef, i} \) es el campo magnético efectivo y \ ({\ overrightarrow {H}} _ {th, i} \) es el campo térmico. El campo magnético efectivo que actúa sobre una nanopartícula separada se puede calcular como una derivada de la energía total del cúmulo

La energía magnética total del cúmulo W = W _a + W _Z + W _m es una suma de la energía de anisotropía magnetocristalina W _a , Energía Zeeman W _Z de las partículas en el campo magnético aplicado \ ({\ overrightarrow {H}} _ 0 \ sin \ left (\ omega t \ right) \), y la energía de interacción mutua magneto-dipolo de las partículas W _m .

Para nanopartículas de forma casi esférica con tipo uniaxial de anisotropía magnética, la energía de anisotropía magnetocristalina viene dada por

donde e _i es la orientación del eje de anisotropía fácil de i -ésima partícula del cúmulo. Energía Zeeman W _Z del grupo en el campo magnético aplicado está dado por

A continuación, para las nanopartículas esféricas uniformemente magnetizadas, la energía magnetostática del cúmulo se puede representar como la energía de los dipolos de interacción puntual ubicados en los centros de partículas r _i dentro del clúster. Entonces, la energía de interacción magneto-dipolo es

donde n _ij es el vector unitario a lo largo de la línea que conecta los centros de i -th y j -ésimas partículas, respectivamente.

Por lo tanto, el campo magnético efectivo que actúa sobre el i -ésima nanopartícula del cúmulo viene dada por

donde H _a =2 K / M _s. es el campo de anisotropía de partículas.

Los campos térmicos, \ ({\ overrightarrow {H}} _ {th, i} \), i =1, 2 ... N _p , actuando sobre varias nanopartículas del clúster son estadísticamente independientes, con las siguientes propiedades estadísticas [39] de sus componentes para cada nanopartícula

Aquí, k _B es la constante de Boltzmann, δ _αβ es el símbolo de Kroneker, y δ ( t ) es la función delta.

El procedimiento para resolver las ecuaciones diferenciales estocásticas. (3), (8) y (9) se describen en detalle en las Refs. [13, 40, 41].

Resultados y discusión

Nanopartículas de óxido de hierro que no interactúan

Considere un ensamblaje diluido de nanopartículas superparamagnéticas con un diámetro promedio D . Se supone que las partículas están empaquetadas de manera apretada en un medio circundante, y sus ejes de anisotropía fáciles están orientados aleatoriamente en el espacio. El bucle de histéresis de tal conjunto en un campo magnético alterno H = H ₀ pecado ( ωt ) se puede calcular [10] usando las Ecs. (1) y (2). Este enfoque, debido a su simplicidad, permite realizar cálculos detallados de los bucles de histéresis del ensamblaje para varios tamaños de partículas dependiendo de la frecuencia y amplitud del campo magnético alterno. En los cálculos realizados, de acuerdo con los datos experimentales [2,3,4,5,6], se supone que la magnetización por saturación de las nanopartículas de óxido de hierro es M _s. =70 am ² / kg, siendo la constante de anisotropía magnética K =10 ⁴ J / m ³ . La temperatura de montaje es T =300 K, y los diámetros de las nanopartículas están en el rango D =10–30 nm. Estos parámetros parecen típicos de los experimentos llevados a cabo con nanopartículas de óxido de hierro.

La Figura 2 muestra el SAR de conjuntos de nanopartículas de óxido de hierro que no interactúan a varias frecuencias a una amplitud fija de campo magnético alterno, H ₀ =8 kA / m. Como puede verse, para el rango de frecuencias que son características de la hipertermia magnética, f =200–500 kHz, SAR tiene un máximo para el ensamblaje de nanopartículas de óxido de hierro con diámetros D =20-21 nm. Es notable que incluso con una amplitud relativamente moderada de un campo magnético alterno, el SAR de ensamblaje alcanza valores suficientemente altos, 350-450 kW / kg, si los diámetros de las nanopartículas se eligen correctamente.

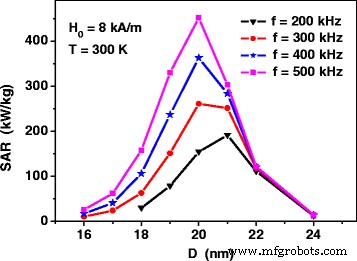
La tasa de absorción específica del ensamblaje no interactuante de nanopartículas de óxidos de hierro, obtenida mediante las Ecs. (1) y (2), en función del diámetro medio de partícula a diferentes frecuencias del campo magnético alterno

Sin embargo, los valores de SAR medidos experimentalmente para conjuntos de nanopartículas de óxidos de hierro están, por regla general, significativamente por debajo [18,19,20,21] de estos valores teóricos. Como veremos en la siguiente sección, este hecho se puede explicar [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] por la influencia de una fuerte interacción magneto-dipolo en conjuntos densos de nanopartículas magnéticas.

Ensamblaje de clústeres 3D

Considere ahora los bucles de histéresis de un conjunto diluido de grupos aleatorios 3D que tienen ejes de anisotropía fáciles de nanopartículas individuales orientadas aleatoriamente en el espacio. Como muestra la Fig. 2, para el ensamblaje de nanopartículas de óxido de hierro que no interactúan, el pico de absorción de energía en un campo magnético alterno corresponde a partículas con diámetro D =20 nm. Por lo tanto, primero calculamos los bucles de histéresis de un ensamblaje de grupos 3D con un diámetro de partícula D =20 millas náuticas.

La figura 3a muestra la evolución de los bucles de histéresis de ensamblaje en función de la distancia media entre los centros de nanopartículas D _av al valor fijo del diámetro de partícula D . La frecuencia y amplitud del campo magnético alterno se fijan en f =400 kHz y H ₀ =8 kA / m, respectivamente. El número de partículas en los grupos es igual a N _p =40. Los cálculos se realizan en T =300 K, y la constante de amortiguamiento magnético se toma como κ =0.5.

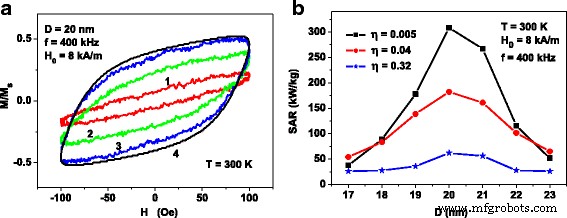
( a ) Evolución de los bucles de histéresis del ensamblaje diluido de grupos de nanopartículas de óxido de hierro de diámetro D =20 nm para varias proporciones D _av / D :( 1 ) D _av / D =1,46; ( 2 ) D _av / D =2,92; ( 3 ) D _av / D =5,84. El bucle de histéresis 4 corresponde al ensamblaje de nanopartículas del mismo diámetro que no interactúan. Se calcula mediante las Ecs. (1) y (2). ( b ) SAR en función del diámetro medio de nanopartículas D para ensamblajes diluidos de grupos de nanopartículas con diferente densidad de empaquetamiento η

Evidentemente, la disminución de la distancia media entre las nanopartículas del cúmulo conduce a un aumento de la intensidad de la interacción magneto-dipolo dentro del cúmulo. Tenga en cuenta que para N _p =40, las proporciones D _av / D especificadas en la Fig. 3a corresponden a las densidades de empaquetamiento de grupos η =0.005, 0.04 y 0.32, correspondientemente. Se puede ver en la Fig. 3a que el área del bucle de histéresis disminuye rápidamente en función del parámetro η . A modo de comparación, la Fig. 3a también muestra el bucle de histéresis 4, calculado para un conjunto de partículas que no interactúan, es decir, en el límite D _av / D → ∞, N _p =Constante, usando las ecuaciones. (1) y (2).

Se puede ver que el ciclo de histéresis 3 ( η =0,005) en la Fig. 3a resulta estar cerca del ciclo de histéresis del ensamblaje de nanopartículas que no interactúan. Por lo tanto, en el caso η ≤ 0,005 la interacción magneto-dipolo de las nanopartículas dentro del grupo puede despreciarse. Sin embargo, para η ≥ 0,04 la interacción magneto-dipolo tiene una influencia significativa en las propiedades de un conjunto de cúmulos tridimensionales aleatorios. Se ha obtenido una evolución similar de los bucles de histéresis de ensamblaje también para las frecuencias f =300 y 500 kHz, respectivamente.

Los bucles de histéresis que se muestran en la Fig. 3a se calculan para diferentes relaciones D _av / D , pero para el número fijo de nanopartículas en el grupo N _p =40. Sin embargo, las simulaciones por computadora detalladas muestran que la forma del bucle de histéresis de un ensamblaje diluido de grupos aleatorios en 3D prácticamente no cambia, si el número de partículas, N _p >> 1 y el radio del grupo R _cl se cambian para que la densidad de empaquetamiento de nanopartículas η permanece constante. Por lo tanto, el ciclo de histéresis del ensamblaje diluido de clústeres 3D aleatorios depende principalmente de la densidad de empaquetado del clúster η .

La Figura 3b muestra el SAR de conjuntos de grupos aleatorios de nanopartículas de óxido de hierro para diferentes η valores. El SAR del conjunto se calcula [10] como SAR = M _s fA / ρ , donde A es el área del bucle de histéresis en las variables ( M / M _s. , H ), ρ siendo la densidad de las nanopartículas de óxido de hierro que se supone que es ρ =5 × 10 ³ kg / m ³ . Como muestra la Fig. 3b, el SAR disminuye en función de η debido a un aumento de la intensidad de la interacción magneto-dipolo dentro de los grupos. Al mismo tiempo, la dependencia del SAR de ensamblaje en el diámetro medio de partícula aún permanece, aunque se vuelve menos pronunciada.

Para valores pequeños de η ≤ 0,005, el SAR del ensamblaje aleatorio de clústeres 3D en realidad coincide con el de un ensamblaje de nanopartículas que no interactúan, que se muestra en la Fig. 2. Por otro lado, el SAR cae unas seis veces cuando la densidad de empaquetado del clúster aumenta hasta η =0,32. Luego, se acerca a los valores típicos de SAR ~ 50–100 kW / kg, que se obtienen en una serie de experimentos [5, 18, 19, 20, 21] con conjuntos de nanopartículas de óxido de hierro.

Ensamblaje de racimos fractales

Se llevaron a cabo cálculos similares para conjuntos diluidos de grupos fractales de nanopartículas con varios descriptores fractales. Como muestra la Fig. 4, para los grupos fractales de nanopartículas, el SAR en función del diámetro de las partículas también disminuye considerablemente con respecto al conjunto de nanopartículas que no interactúan. Sin embargo, a diferencia del ensamblaje de grupos 3D, los valores máximos de SAR se desplazan sistemáticamente a diámetros de partículas más pequeños, excepto en el caso de la dimensión fractal D _f =2.7, que se acerca al caso de los clústeres 3D con D _f =3,0. Es interesante observar también que para diámetros de nanopartículas no óptimos, por ejemplo, para nanopartículas con diámetros D ≤ 17 nm, la influencia de la interacción magneto-dipolo conduce a un aumento del SAR con respecto al caso de ensamblaje de nanopartículas que no interactúan, ya que el SAR del ensamblaje de nanopartículas que no interactúan es muy pequeño para nanopartículas con diámetros D ≤ 17 nm.

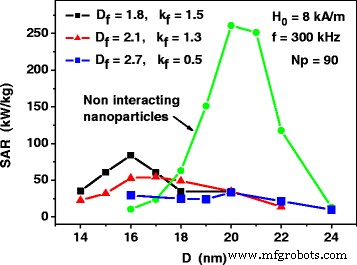
SAR en función del diámetro medio de nanopartículas D para diluir ensamblajes de grupos fractales de nanopartículas con varios descriptores fractales. El SAR del ensamblaje de nanopartículas que no interactúan se calcula mediante las Ecs. (1) y (2)

Los cálculos que se muestran en la Fig.4 se llevaron a cabo asumiendo la existencia de capas delgadas no magnéticas con un espesor t _Sh =1 nm en la superficie de nanopartículas magnéticas. Esto evita que las nanopartículas del cúmulo fractal de interacción de intercambio directo. Evidentemente, el aumento del espesor de la capa no magnética reduce la intensidad de la interacción magneto-dipolo de las nanopartículas más cercanas, a medida que aumenta la distancia promedio entre los núcleos magnéticos de las nanopartículas. Figure 5 shows that the increase of the non-magnetic shell thickness is a proper way to raise the SAR of the assembly of fractal clusters of nanoparticles. Namely, for sufficiently large thickness of non-magnetic shells the dependence of the SAR on the particle diameter resembles that for weakly interacting magnetic nanoparticles. This fact may be important for the application of magnetic nanoparticle assemblies in magnetic hyperthermia.

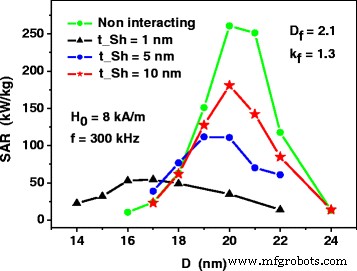
The dependence of the SAR of dilute assembly of fractal clusters on the thickness t _Sh of the non-magnetic shells at the surface of the nanoparticles. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

Conclusiones

The main conclusion of this study is that the SAR of a dilute assembly of clusters of magnetic nanoparticles in alternating magnetic field is significantly reduced with increasing of the intensity of magneto-dipole interaction in the clusters. For usual 3D clusters of nanoparticles, the intensity of the magneto-dipole interaction can be characterized by dimensionless packing density, η  = N _p V / V _cl  = (D /D _av ) ³ . The latter determines the average distance between the nanoparticles of the cluster. The calculations show that for the assembly of random 3D clusters, the energy absorption peak, which for iron oxide nanoparticles corresponds to particles with average diameter D  = 20 nm, is reduced about six times when the packing density increases from η  = 0.005 up to η  = 0.32. The dependence of the assembly SAR on the mean nanoparticle diameter is retained with increase of η , but becomes less pronounced.

For dilute assemblies of fractal clusters of magnetic nanoparticles, the SAR values also decrease several times irrespective on the fractal descriptors of the assembly. In addition, the peak values of SAR are shifted systematically to smaller particle diameters, as a rule. It is important to note, however, that the increase of the non-magnetic shell thickness at the nanoparticle surfaces restores the SAR values close to that of the assembly of weakly interacting nanoparticles. This fact can be important for various biomedical applications of magnetic nanoparticle assemblies.

The model considered in this paper takes into account the geometrical structure of nanoparticle assemblies observed experimentally in biological media [4, 8, 9] (in particular in tumors), i.e., the agglomeration of nanoparticles in a sufficiently dense fractal clusters of different sizes, with different numbers of nanoparticles in the clusters. The stochastic LL Eq. (3) accurately describes the real dynamics of the magnetic moments of nanoparticles taking into account both the magneto-dipole interaction between the particles and the effect of thermal fluctuations. The cluster model studied allows obvious generalization that can make it more practical. First, it is necessary to take into account the size distribution of magnetic nanoparticles in the assembly. Second, in some cases exchange interaction may exist between neighboring nanoparticles of the cluster if they are in direct atomic contact.

The theoretical results obtained in this study seem to be in a satisfactory agreement with recent experimental data [35] for iron oxide nanoparticles of optimal diameters. Indeed, according to Ref. [35], the SAR of the iron oxide nanoparticles increases with the average diameter of the nanoparticles and peaks for nanoparticles with mean diameter D  = 20–21 nm. In addition, the SAR decreases [35] with a decrease in the average distance between the nanoparticles due to increasing intensity of the magneto-dipole interaction.

Unfortunately, in some experimental studies [5, 21] carried out to optimize the properties of magnetic nanoparticles for use in magnetic hyperthermia, often do not take into account the theoretical predictions [10, 11] about significant dependence of the assembly SAR on the characteristic size of the magnetic nanoparticles. As shown in this paper, this dependence can be substantial even for rather dense nanoparticle assemblies. From a theoretical point of view, it is obvious [10] that the assembly of iron oxide nanoparticles with very small, D  ≤ 10 nm, or too big, D  ≥ 30 nm diameters can hardly provide a sufficiently high SAR values for typical for magnetic hyperthermia frequencies, f  = 200–600 kHz, and magnetic field amplitudes H ₀  ~ 8 kA/m. The creation of mono-crystalline iron oxide nanoparticles with sharp size distribution near the optimal diameter has to be promising for application in magnetic hyperthermia.

Un nuevo sensor inteligente de dispersión Raman mejorado en la superficie basado en nanopartículas de ag con tapa de poliacriloilhidrazina que responden al pH Hacia cadenas de átomos individuales con telurio exfoliado