Efectos del tamaño y la agregación / aglomeración de las nanopartículas en las propiedades interfaciales / interfásicas y la resistencia a la tracción de los nanocompuestos poliméricos

Resumen

En este estudio, se sugieren varias ecuaciones simples para investigar los efectos del tamaño y la densidad en el número, el área de superficie, la eficiencia de endurecimiento y el área de superficie específica de nanopartículas en nanocompuestos de polímeros. Además, las funciones del tamaño de las nanopartículas y el grosor de la interfase en las propiedades interfaciales / interfásicas y la resistencia a la tracción de los nanocompuestos se explican mediante varias ecuaciones. Los agregados / aglomerados de nanopartículas también se asumen como partículas grandes en nanocomposites, y se discuten sus influencias en las características de las nanopartículas, propiedades de interfaz / interfase y resistencia a la tracción. El tamaño pequeño afecta ventajosamente el número, el área de la superficie, la eficacia de endurecimiento y el área de la superficie específica de las nanopartículas. Solo 2 g de nanopartículas aisladas y bien dispersas con un radio de 10 nm ( R =10 nm) y densidad de 2 g / cm ³ producir el área interfacial significativa de 250 m ² con matriz de polímero. Además, solo una interfase gruesa no puede producir parámetros de interfase / interfase elevados y propiedades mecánicas significativas en los nanocompuestos porque el tamaño del relleno y los agregados / aglomerados también controlan estos términos. Se encuentra que una interfase gruesa ( t =25 nm) que rodean las grandes nanopartículas ( R =50 nm) solo mejora la B parámetro de interfase a aproximadamente 4, mientras que B =13 se obtiene mediante las nanopartículas más pequeñas y la interfase más gruesa.

Antecedentes

Los nanocomposites exhiben propiedades sustanciales por solo un pequeño contenido de nanorrelleno [1, 2, 3, 4, 5]. Las importantes propiedades de los nanocompuestos poliméricos provocan una amplia gama de aplicaciones en diversas tecnologías, como materiales y bienes avanzados, medicamentos, dispositivos de energía y sensores [6]. Los estudios sobre diferentes tipos de nanocompuestos poliméricos tienen como objetivo lograr productos de alto rendimiento mediante un proceso de fabricación sencillo y de bajo costo.

Las considerables propiedades de los nanocompuestos poliméricos se atribuyen a las buenas propiedades interfaciales entre la matriz polimérica y las nanopartículas, como el área interfacial y la interacción / adhesión en la interfaz [7,8,9,10,11,12,13]. Los altos niveles de propiedades interfaciales conducen a la formación de otra fase como interfase alrededor de las nanopartículas, que es diferente tanto de la matriz polimérica como de las nanopartículas, lo que muestra la ventaja de los nanocompuestos en comparación con los microcompuestos convencionales [14, 15, 16, 17, 18]. Muchas investigaciones teóricas sobre propiedades interfaciales / interfásicas han proporcionado una gran cantidad de información para lograr las propiedades deseables. Sin embargo, la gran superficie de las nanopartículas y la fuerte interacción atractiva entre las partículas dan como resultado la agregación / aglomeración [19, 20]. Los colectivos fuertes y densos de nanopartículas denotan la agregación, pero las partículas unidas sueltas muestran la aglomeración que puede romperse por tensión mecánica [21].

La agregación / aglomeración de nanopartículas reduce la potencial mejora de las propiedades mecánicas en nanocomposites, debido a la restricción del área interfacial [22, 23]. Por tanto, el principal desafío en la producción de nanocomposites incluye la consecución de pequeñas nanopartículas y una buena dispersión de nanopartículas. Es vital superar las fuerzas de atracción entre nanopartículas que producen la agregación / aglomeración, en lugar de alterar la estructura de las nanopartículas. Sorprendentemente, Dorigato et al. [24] sugirió un modelo que muestra que la agregación del relleno primario refuerza los nanocompuestos poliméricos, mientras que las nanopartículas aglomeradas comúnmente inducen efectos negativos sobre las prestaciones mecánicas de los nanocompuestos poliméricos [21, 25]. En consecuencia, se requiere el estudio de agregación / aglomeración de nanopartículas para revelar sus efectos reales sobre las propiedades de los nanocomposites. Aunque se supone que el tamaño de las nanopartículas es un beneficio atractivo en los nanocompuestos de polímeros, los efectos del aislamiento o agregación / aglomeración sobre las principales propiedades de las nanopartículas, como el número, el área de superficie y el área de superficie específica, no se han estudiado en la literatura. Además, la agregación / aglomeración de nanopartículas se ha asumido como un término general que cambia cualitativamente el comportamiento de los nanocomposites. Además, los posibles roles de las dimensiones de las nanopartículas y la interfase en las propiedades interfaciales / interfásicas no se han descrito en estudios anteriores.

Métodos

En este artículo, los efectos del tamaño y la densidad del relleno sobre el número, el área de superficie, la eficiencia de endurecimiento y el área de superficie específica de las nanopartículas en nanocompuestos de polímeros se explican mediante ecuaciones adecuadas. Además, la agregación / aglomeración de nanopartículas se asume como partículas grandes y se revelan sus influencias en varios términos. De manera similar, se discuten los posibles roles de los tamaños de las nanopartículas y de la interfase en los parámetros interfaciales / interfásicos y la resistencia a la tracción de los nanocompuestos. El enfoque principal de este artículo son las nanopartículas esféricas, pero se pueden estudiar otras geometrías de nanopartículas mediante el desarrollo de las ecuaciones sugeridas.

El número de nanopartículas aisladas esféricamente en un nanocompuesto se puede calcular por el peso de las nanopartículas ( W _f ) como:

$$ N =\ frac {W_f} {d_f \ frac {4} {3} \ pi {R} ^ 3}. $$ (1)

donde d _f y R son la densidad y el radio de las nanopartículas, respectivamente. En esta condición, el área de superficie total de nanopartículas dispersas viene dada por:

$$ A =N \ left (4 \ pi {R} ^ 2 \ right). $$ (2)

A puede considerarse como el área interfacial entre la matriz polimérica y las nanopartículas. Reemplazo de N de la ecuación. 1 en la ecuación. 2 conduce a:

$$ A =\ frac {3 {W} _f} {d_fR}. $$ (3)

que correlaciona la A con W _f , d _f y R .

Cada nanopartícula introduce un efecto de endurecimiento en la matriz polimérica mediante la participación mecánica de las cadenas poliméricas. El nivel de estrés compartido entre la matriz polimérica y las nanopartículas depende del área interfacial y la rigidez de las nanopartículas. Como resultado, un parámetro novedoso como la eficiencia de refuerzo de las nanopartículas se puede definir como:

$$ SE ={AE} _f =\ frac {3 {W} _f} {d_fR} {E} _f. $$ (4)

donde E _f es el módulo de nanopartículas de Young. La eficiencia de endurecimiento en función de las propiedades de las nanopartículas expresa la capacidad de las nanopartículas para endurecer los nanocompuestos. Además, el área de superficie específica de las partículas se expresa como:

$$ {A} _c =\ frac {A} {m} =\ frac {A} {d_fv} =\ frac {4 \ pi {R} ^ 2} {d_f \ frac {4} {3} \ pi { R} ^ 3} =\ frac {3} {d_fR}. $$ (5)

donde m y v son la masa total y el volumen de nanopartículas, respectivamente. Este parámetro expresa el área de superficie de partículas de 1 g, por lo que no depende de la concentración de nanopartículas en el nanocompuesto.

Ahora, la resistencia a la tracción y las propiedades interfaciales / interfásicas vienen dadas por ecuaciones simples. Pukanszky [26] sugirió un modelo para la resistencia a la tracción de los compuestos en función del contenido de relleno y las propiedades interfaciales / interfásicas como:

$$ \ sigma ={\ sigma} _m \ frac {1 - {\ varphi} _f} {1 + 2.5 {\ varphi} _f} \ exp \ left (B {\ varphi} _f \ right). $$ (6)

donde σ _m muestra la resistencia a la tracción de la matriz de polímero y φ _f es la fracción de volumen del nanorrelleno. Este modelo se sugirió originalmente para compuestos, pero este modelo ha mostrado buenas concordancias con los resultados experimentales de diferentes nanocompuestos de polímeros. Se obtiene una buena concordancia entre los datos experimentales de resistencia a la tracción y las predicciones de la ecuación de Pukanszky en muchas muestras como PP / SiO ₂ [27], PEEK / SiO ₂ [28], PVC / CaCO ₃ [29], PP / CaCO ₃ [30] y PVC / SiO ₂ [31] cálculo de B parámetro como 4.12, 3.15, 3.07, 2.5 y 2.1, respectivamente. Estos ejemplos validan la aplicación del modelo Pukanszky para la resistencia a la tracción de nanocompuestos poliméricos.

B es un parámetro interfacial que muestra el nivel de adhesión interfacial mediante:

$$ B =\ left (1+ {A} _c {d} _ft \ right) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right). $$ (7)

donde t y σ _i son el grosor y la fuerza de la interfase, respectivamente.

Reemplazo de A _c de la ecuación. 5 en la última ecuación presenta:

$$ B =\ left (1 + 3 \ frac {t} {R} \ right) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right). $$ (8)

La aplicación de la ecuación anterior en el modelo de Pukanszky ofrece la fuerza relativa ( σ / σ _m ) como:

$$ {\ sigma} _R =\ frac {1 - {\ varphi} _f} {1 + 2.5 {\ varphi} _f} \ exp \ left [\ left (1 + 3 \ frac {t} {R} \ right ) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right) {\ varphi} _f \ right]. $$ (9)

que vincula explícitamente la resistencia a la tracción con el relleno y las propiedades de interfase. Además, debemos indicar los efectos de tamaño, que sin duda existen al modelar la fractura [32,33,34].

La fracción de volumen de la interfase ( φ _i ) para nanocompuestos que contienen nanopartículas esféricas puede ser considerado [35] por:

$$ {\ varphi} _i =\ left [{\ left (\ frac {R + t} {R} \ right)} ^ 3-1 \ right] {\ varphi} _f. $$ (10)

en el que t =0 resultados en φ _i =0 indica la ausencia de interfase en nanocompuestos. Los modelos analíticos de este estudio pueden ser aplicables cuando otros modelos, como la zona cohesiva, describen las regiones de interfase. Algunos estudios previos han considerado la interfase por algunos modelos como el elemento finito 2D [36, 37].

En nuestro trabajo anterior [38], a El parámetro de interfase para nanocompuestos poliméricos reforzados con nanopartículas esféricas se definió como:

$$ a =10 \ left (\ frac {t} {R} \ right) \ left (\ frac {10 {E} _i} {E_f} -1 \ right). $$ (11)

donde E _i es el módulo de interfase. Esta ecuación correlaciona la a a varios parámetros efectivos de nanorelleno e interfase. a se calculó para algunos nanocompuestos en un rango de 0,8 a 19 [38]. Se informó que un nivel más alto de a introduce un mejor módulo en nanocompuestos.

Resultados y discusión

En la primera parte de esta sección, los efectos del tamaño y la densidad en las diferentes propiedades de las nanopartículas se representan mediante gráficos de contorno y los resultados se discuten para aclarar la influencia de la agregación / aglomeración. En el siguiente paso, se estudian las funciones del radio de las nanopartículas (incluida la agregación / aglomeración) y el grosor de la interfase en las propiedades interfaciales / interfásicas y el rendimiento de los nanocompuestos.

La Figura 1 ilustra la agregación / aglomeración de nanopartículas en un nanocompuesto. Cuando se acumulan las nanopartículas aisladas y dispersas, se puede suponer que se forma una gran nanopartícula. Según la figura 1, si se aíslan nanopartículas con R agregado / aglomerado de radio, se produce una partícula grande con un radio alto. Como resultado, la agregación / aglomeración de nanopartículas puede asumirse físicamente mediante el crecimiento del tamaño de partícula en nanocomposites. Esta ocurrencia afecta las características de las nanopartículas y la interfase que finalmente cambia el comportamiento de los nanocomposites.

Ilustración esquemática de agregación / aglomeración de nanopartículas en nanocompuestos poliméricos. Cuando varias nanopartículas con radio R se agregan / aglomeran, se forma una partícula grande

La Figura 2 muestra los roles de R y d _f en ln (N) y A niveles a W constante _f =2 g. De acuerdo con la Fig. 2a, bajo N es observado por los valores altos de R y d _f , pero N aumenta cuando R y d _f disminución. Por lo tanto, la densidad y el tamaño de las nanopartículas afectan inversamente al número de partículas en los nanocompuestos de polímero a una concentración constante de relleno. Las nanopartículas pequeñas con baja densidad producen una gran cantidad de nanopartículas en nanocompuestos, mientras que las nanopartículas grandes y densas producen pocas partículas. En consecuencia, los agregados / aglomerados disminuyen significativamente el número de nanopartículas en los nanocompuestos a una concentración constante de relleno.

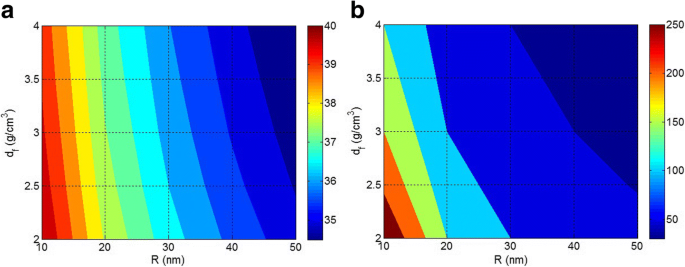
Gráficos de contorno para mostrar los roles de R y d _f parámetros en a En ( N ) y b A (m ² ) en W _f =2 g

La figura 2b ilustra los efectos de R y d _f parámetros sobre la superficie total de nanopartículas ( A en m ² ) en W _f =2 g. Se asume que el área de superficie de las nanopartículas es el área interfacial entre el polímero y las nanopartículas que transfieren el estrés de la matriz a las nanopartículas. La tensión puede transportarse de manera eficiente desde el polímero a las nanopartículas para mejorar las propiedades mecánicas, cuando el área interfacial es lo suficientemente grande [39, 40]. Como se observa en la Fig. 2b, el área interfacial más grande se logra con los rangos más pequeños de R y d _f . También es interesante que solo 2 g de nanopartículas aisladas y bien dispersas con R =10 nm y d _f =2 g / cm ³ producir alrededor de 250 m ² área interfacial con matriz de polímero. Sin embargo, el área interfacial se reduce al aumentar el tamaño y la densidad de las nanopartículas y A por debajo de 50 m ² se obtiene en R > 40 nm y d _f> 3 g / cm ³ . La diferencia significativa entre las áreas interfaciales en diferentes tamaños de partículas indica que el tamaño de las nanopartículas es un parámetro importante en los nanocompuestos. Las nanopartículas grandes provocan una pequeña área interfacial que deteriora la ventaja significativa de las nanopartículas en los nanocompuestos. Cabe señalar que la concentración de relleno en los nanocompuestos puede no ser demasiado alta en comparación con los microcompuestos, pero la extraordinaria área de superficie de las nanopartículas comúnmente da como resultado la interacción entre las partículas y la agregación / aglomeración. Como resultado, aunque los altos contenidos de nanopartículas en los nanocompuestos fortalecen la acumulación, la agregación / aglomeración de nanopartículas generalmente ocurre en nanocompuestos poliméricos a diferentes concentraciones de relleno que disminuyen el área interfacial y debilitan el rendimiento.

La Figura 3a muestra las gráficas de contorno de ln (SE) en función de R y d _f en W _f =2 gy E _f =100 GPa. La eficiencia de endurecimiento de las nanopartículas aumenta cuando se incorporan pequeñas nanopartículas de baja densidad en la matriz polimérica, lo que demuestra que el tamaño de las nanopartículas tiene un papel eficaz en el endurecimiento de las nanopartículas en los nanocompuestos poliméricos. Por otro lado, las nanopartículas agregadas / aglomeradas deterioran el rendimiento de los nanocompuestos poliméricos al reducir la eficiencia de las nanopartículas. Las pequeñas nanopartículas de baja densidad aumentan significativamente la rigidez de los nanocompuestos a través del gran nivel de transferencia de tensión entre las cadenas de polímeros y las nanopartículas. Un estudio anterior en esta área ha explicado la física de la influencia del radio de relleno en la transferencia de tensión de la matriz de polímero a la fibra utilizando simulaciones de dinámica molecular [41]. Sin embargo, las partículas grandes y densas no pueden introducir la alta rigidez de las nanopartículas en la matriz del polímero, lo que sugiere un compuesto con poca rigidez. Por tanto, las características de las nanopartículas controlan significativamente las propiedades de los nanocompuestos.

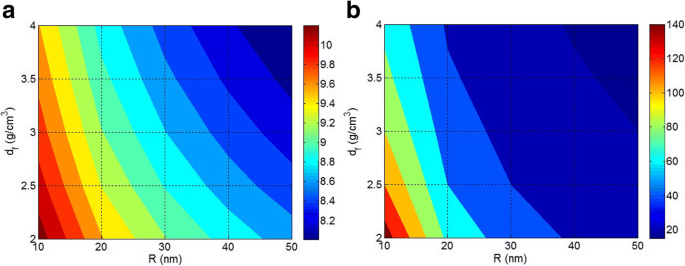
Los efectos de R y d _f el a ln (SE) con ln (m ² GPa) unidad y b A _c (m ² / g) en W _f =2 gy E _f =100 GPa

La Figura 3b también muestra los niveles de A _c parámetro en diferentes R y d _f valores en W _f =2 gy E _f =100 GPa. Se observa que la mejor A _c se obtiene por nanopartículas pequeñas y de baja densidad, mientras que la peor es producida por partículas grandes y densas. La A _c valor de aproximadamente 140 m ² / g se logra con R =10 nm y d _f =2 g / cm ³ , mientras que A _c nivel de menos de 20 m ² / g se muestra por gran tamaño de partícula y alta densidad. Como resultado, R y d _f los parámetros muestran efectos negativos en A _c en nanocomposites poliméricos. Se concluye que A _c El parámetro que expresa el área interfacial de 1 g de nanopartículas aisladas da los mejores niveles por nanopartículas pequeñas. Como resultado, las grandes nanopartículas o agregados / aglomerados no pueden producir una cantidad considerable de A _c lo que disminuye la eficiencia de las nanopartículas en nanocompuestos poliméricos. Se sabe que las prestaciones de los nanocomposites, como las propiedades mecánicas, de retardo de llama y de barrera, se relacionan directamente con el área interfacial entre el polímero y las nanopartículas [10, 42]. Una A grande _c puede producir niveles aceptables de propiedades de nanocompuestos por una pequeña cantidad de nanopartículas, debido a la alta área interfacial entre la matriz polimérica y las nanopartículas. En consecuencia, controlar el tamaño y la densidad de las nanopartículas es un desafío en los nanocompuestos para crear las mejores propiedades.

Ahora, los efectos de los tamaños de las nanopartículas y de la interfase sobre las propiedades interfaciales / interfásicas y la resistencia a la tracción de los nanocompuestos se explican mediante las ecuaciones propuestas. La Figura 4 ilustra los efectos de R y t en B Parámetro interfacial y resistencia a la tracción según el modelo de Pukanszky (Ec. 6) en σ _i / σ _m =5 y φ _f =0,02. Basado en la Fig. 4a, el B El nivel 13 se obtiene mediante las nanopartículas más pequeñas y la interfase más gruesa. Además, B disminuye por debajo de 3 cuando el tamaño de las nanopartículas crece a aproximadamente 40 nm y el espesor de la interfase disminuye a menos de 10 nm. Por lo tanto, los tamaños de las nanopartículas y la interfase desempeñan funciones diferentes en B parámetro. Además, debe tenerse en cuenta que las nanopartículas pequeñas sin la formación de una interfase fuerte no pueden dar un B alto en nanocomposites poliméricos. Por otro lado, una interfase gruesa ( t =25 nm) que rodean las grandes nanopartículas ( R =50 nm) solo mejora la B parámetro a aproximadamente 4. Como resultado, las dimensiones de las nanopartículas y de la interfase son importantes para obtener un alto nivel de B en nanocomposites. Sin embargo, a un nivel constante de espesor de interfase, el crecimiento del tamaño de las nanopartículas por agregación / aglomeración disminuye B parámetro que demuestra los efectos negativos de los agregados / aglomerados en las propiedades interfaciales / interfásicas.

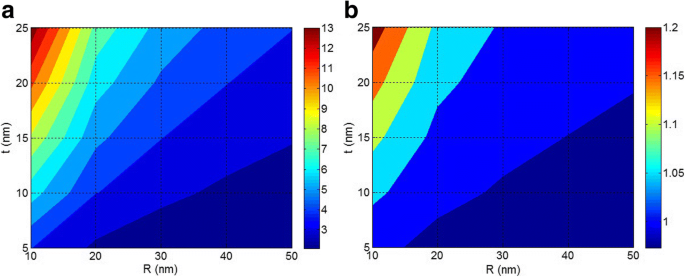
un B parámetro interfacial y b resistencia a la tracción relativa según el modelo de Pukanszky en diferentes rangos de R y d _f y constante σ _i / σ _m =5 y ϕ _f =0.02

La Figura 4b también muestra los efectos de R y t parámetros sobre la resistencia a la tracción de nanocomposites por modelo de Pukanszky. Se observa que las nanopartículas pequeñas y la interfase gruesa mejoran la resistencia de los nanocomposites. Sin embargo, las partículas grandes y la interfase delgada observan una resistencia deficiente. Por lo tanto, tanto R y t Los parámetros afectan la resistencia a la tracción de los nanocomposites. Además, se encuentra que la resistencia de los nanocomposites se reduce cuando aumenta el tamaño de las nanopartículas, debido a la agregación / aglomeración. En consecuencia, es fundamental aislar y dispersar las nanopartículas en una matriz polimérica de pequeño tamaño para lograr los mejores rendimientos. Dado que las nanopartículas tienden naturalmente a la agregación / aglomeración, la modificación de su superficie o la funcionalización de las cadenas de polímeros pueden prevenir la acumulación [19, 43, 44].

La Figura 5 muestra las dependencias de la fracción de volumen en interfase ( φ _i ) y a parámetro de interfase en R y t parámetros en φ _f =0.02, E _f =100 GPa y E _i =50 GPa. Según la Fig. 5a, las nanopartículas más pequeñas y la interfase más gruesa dan el nivel más alto de φ _i como 0.8 lo que refuerza significativamente el nanocompuesto. Este nivel de φ _i es más que φ _f demostrando los roles efectivos de R y t parámetros en el rendimiento de nanocomposites. Además, φ _i disminuye a aproximadamente 0 en R > 30 nm, es decir, una interfase gruesa ( t =25 nm) no puede hacer un φ alto _i en nanocompuestos poliméricos cuando se incorporan grandes nanopartículas en la matriz polimérica. Esta ocurrencia muestra el papel significativo del tamaño de las nanopartículas en la formación de regiones de interfase. Por lo tanto, el tamaño de las nanopartículas cambia considerablemente las propiedades de la interfase, revelando que la agregación / aglomeración de las nanopartículas disminuye principalmente la concentración de la interfase, lo que provoca un módulo y una resistencia deficientes en los nanocompuestos [5, 45]. Cabe mencionar que las regiones de interfase pueden solaparse en los sistemas que contienen una alta concentración de carga. Por lo tanto, la ecuación expresada para φ _i (Ec. 10) es razonable para nanocomposites normales que contienen bajo contenido de relleno.

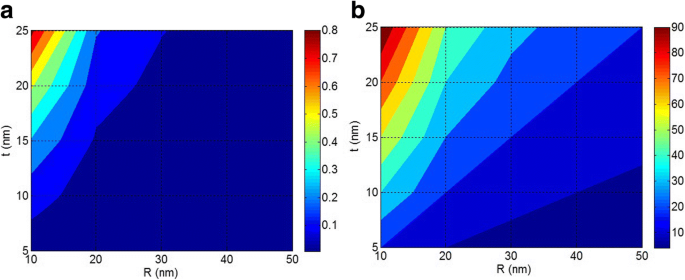
La correlación de a ϕ _i y b a parámetro de interfase a R y t parámetros en ϕ _f =0.02, E _f =100 GPa y E _i =50 GPa

La Figura 5b también muestra los efectos de R y t niveles en a parámetro de interfase. a aumenta por nanopartículas pequeñas e interfase gruesa, mientras que da menos valores (menos de 10) en R > 40 nm y t <10 nm. Esta evidencia revela que a depende tanto de R y t parámetros. Desde un alto a El parámetro mejora el módulo de Young de los nanocompuestos [38], las nanopartículas pequeñas y la interfase gruesa son deseables para los rendimientos de los nanocompuestos. Según la Fig. 5b, los agregados / aglomerados de nanopartículas (alto R ) producen una ligera a evento por interfase gruesa. Esta ocurrencia indica que una interfase fuerte no puede dar una gran a o módulo alto cuando las nanopartículas se agregan / aglomeran en nanocomposites. Como resultado, los agregados / aglomerados de nanopartículas causan efectos negativos sobre las propiedades de los nanocompuestos poliméricos. Con base en las observaciones mencionadas, la agregación / aglomeración debilita los beneficios de las nanopartículas y las propiedades de interfaz / interfase; por tanto, las nanopartículas no pueden presentar un refuerzo fuerte en nanocompuestos poliméricos.

Conclusiones

Los efectos del tamaño y la densidad del relleno, así como el espesor de la interfase sobre las características de las nanopartículas y las propiedades de interfaz / interfase, se estudiaron mediante ecuaciones simples. Además, los agregados / aglomerados de nanopartículas se asumieron como partículas grandes y se discutieron sus influencias en los parámetros de interfase y la resistencia a la tracción de los nanocompuestos. El tamaño pequeño y la baja densidad provocan niveles significativos de número, área de superficie, eficiencia de endurecimiento y área de superficie específica de nanopartículas. Solo 2 g de nanopartículas pequeñas y bien dispersas ( R =10 nm) con d _f =2 g / cm ³ puede producir unos 250 m ² área interfacial con matriz de polímero. Por otro lado, el gran tamaño y los agregados / aglomerados debilitan los atributos positivos de las nanopartículas en los nanocompuestos. Las nanopartículas pequeñas y la interfase gruesa presentan los niveles altos de B parámetro, resistencia a la tracción, fracción de volumen de interfase y a parámetro de interfase. B disminuye por debajo de 3 cuando el tamaño de las nanopartículas crece hasta aproximadamente 40 nm y el espesor de la interfase se reduce a menos de 10 nm. Sin embargo, B =13 se obtiene por las nanopartículas más pequeñas ( R =10 nm) y la interfase más gruesa ( t =25 nm). Este hecho confirma que las propiedades interfaciales / interfásicas dependen del tamaño de la nanopartícula además de la interacción / adhesión interfacial. Además, las nanopartículas grandes producen propiedades de interfase / interfaces bajas y poca resistencia a la tracción incluso con espesores de interfase altos, lo que revela el papel principal del tamaño de las partículas. Las nanopartículas más pequeñas y la interfase más gruesa dan el nivel más alto de φ _i , mientras que φ _i disminuye a aproximadamente 0 en R > 30 nm. Esta evidencia demuestra que solo una interfase gruesa ( t =25 nm) no puede hacer un φ alto _i cuando grandes nanopartículas o agregados / aglomerados están presentes en nanocompuestos. En consecuencia, las nanopartículas agregadas / aglomeradas afectan negativamente las propiedades interfaciales / interfásicas y la resistencia a la tracción de los nanocompuestos poliméricos.

Tensioactivo aniónico / Líquidos iónicos Intercalado de óxido de grafeno reducido para supercondensadores de alto rendimiento Un estudio de la variabilidad en la memoria de acceso aleatorio resistivo de contacto por modelo de vacante estocástico

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias