Magnetismo de percolación en nanopartículas ferroeléctricas

Antecedentes

La fabricación y los estudios intensos de nanopartículas a partir de óxidos dieléctricos, que no son magnéticos a granel, revelaron el ferromagnetismo en ellas, por ejemplo, en HfO ₂ [1], TiO ₂ [2,3,4], ZnO [5,6,7], SnO ₂ [7, 8], KTaO ₃ [9] y KNbO ₃ [10]. Se consideraron diferentes orígenes de los fenómenos, tales como clusters metálicos, fases secundarias, polarones magnéticos ligados, portadores de carga y vacantes de oxígeno [2, 3, 5, 8,9,10,11,12,13]. Estos últimos se hibridan cerca de la superficie de las nanopartículas, adquiriendo así propiedades magnéticas [12, 13]. Actualmente, las explicaciones siguen siendo controvertidas y no existe consenso sobre el origen del ferromagnetismo. Por tanto, la actividad investigadora continúa en esa dirección.

Entre los ferroeléctricos, recientemente, en nanocristales (el tamaño medio de partícula es de 80 nm) de tantalato de potasio y niobato de potasio, producidos por la nueva tecnología de oxigenación del metal (Ta o Nb) en nitrato de potasio fundido [14], métodos de resonancia magnética y magnetización estática estableció experimentalmente la aparición de un subsistema ferromagnético junto con un subsistema paramagnético [10, 15, 16]. Este efecto está ausente en cristales más grandes (con tamaños> 200 nm) de los compuestos obtenidos por la misma tecnología. Los compuestos no son magnéticos en su mayor parte. El dopaje intencional de tantalato de potasio (KNbO ₃ ) y niobato de potasio (KTaO ₃ ) Los nanocristales de hierro y manganeso por separado dieron como resultado el aumento del componente paramagnético, mientras que el subsistema ferromagnético permanece sin cambios [15, 16]. Se ha sugerido que la razón de la aparición de las propiedades magnéticas de los nanocristales ferroeléctricos prístinos son defectos magnéticos, que pueden ser tanto átomos de impurezas de hierro, que forman grupos metálicos en la superficie de las nanopartículas, como vacantes de oxígeno [9]. Además de los métodos experimentales antes mencionados, esta suposición se basó en los datos del análisis elemental y estimaciones teóricas.

Para determinar el mecanismo microscópico del fenómeno observado, en este trabajo analizamos la situación utilizando una teoría de la percolación. La teoría de la percolación describió bastante bien una serie de efectos en sistemas magnéticos desordenados, antes en ferrodieléctricos [17], más tarde en semiconductores magnéticos diluidos (por ejemplo, [18,19,20,21]). El subsistema magnético se trata como un polarón magnético ligado en semiconductores diluidos. Este modelo fue propuesto en primer lugar por los autores de [22] y posteriormente desarrollado por los autores de las Refs. [11, 23].

Asumiendo el papel dominante de las vacantes de oxígeno, usamos el modelo de polarones magnéticos ligados y encontramos el radio de percolación en el que las interacciones de intercambio entre los electrones atrapados en las vacantes de oxígeno mediadas por iones de impurezas magnéticas inducen un orden ferromagnético superficial en KTaO ferroeléctrico ₃ y KNbO ₃ nanopartículas.

Datos experimentales y modelo de ordenamiento ferromagnético

Para justificar el modelo propuesto de ordenamiento ferromagnético, en un primer momento, exponemos los datos experimentales obtenidos sobre las nanopartículas ferroeléctricas КTaO ₃ (KTO) y KNbO ₃ (KNO).

Las nanopartículas ferroeléctricas examinadas son nominalmente puras, es decir, no se incorporaron especialmente dopantes. Sin embargo, el análisis elemental realizado con un espectrómetro de emisión atómica de plasma acoplado inductivamente (ICP-AES) Shimadzu ICPE-9000 muestra que el Fe está presente en ambos materiales como impureza inevitable en una cantidad de 0.06% molar en КTaO ₃ y 0,008% en moles en KNbO ₃ . También se sabe que las vacantes de oxígeno siempre existen en los ferroeléctricos de óxido, como el tipo perovskita (fórmula general ABO ₃ ), lo que da como resultado cierto grado de no estequiometría en estos compuestos. Se ha demostrado experimentalmente que dos subsistemas magnéticos (paramagnético y ferromagnético) están presentes en los nanocristales KTaO ₃ y KNbO ₃ [9, 10, 15]. El subsistema paramagnético consta de Fe ³⁺ magnético que no interactúa iones en KTaO ₃ y Fe ³⁺ y Mn ²⁺ iones en KNbO ₃ . Además, la estructura del centro paramagnético, determinada a partir de mediciones de resonancia paramagnética electrónica (EPR), incluye una vacante de oxígeno V (O), que reduce la simetría del centro [9, 15]. A título ilustrativo, dos tipos de centros paramagnéticos, de simetría axial y rómbica, en los que Fe ³⁺ ion reemplaza Ta ⁵⁺ (o Nb ⁵⁺ ), se muestran en la Fig. 1. Para alcanzar la compensación de carga, se forman una (centro axial) o dos (centro rómbico) vacantes de oxígeno V (O) en la estructura de estos centros.

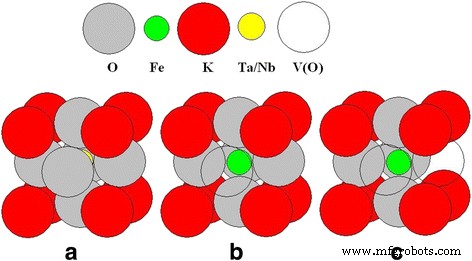
Modelos de centros paramagnéticos de baja simétrica de Fe ³⁺ en KTaO ₃ y KNbO ₃ nanocristales. un Celda unitaria sin defectos, b Fe axial ³⁺ -V (O) centro y c Fe rómbico ³⁺ -2 V (O) centro

Como se sugiere en los artículos [9, 15], el subsistema ferromagnético es un grupo (s) de superficie que consta de átomos de hierro y vacantes de oxígeno. El recocido térmico en una atmósfera de oxígeno, realizado en el artículo [9], muestra que las vacantes de oxígeno definitivamente contribuyen a la formación de ferromagnetismo en estos compuestos. Por un lado, las vacantes se hibridan y se vuelven magnéticas cerca de la superficie de las nanopartículas [13]. Por otro lado, los electrones que emergen de forma inherente en óxidos no estequiométricos a menudo quedan atrapados por las vacantes de oxígeno. En ambos casos, la vacante de oxígeno tiene un giro S =½ y tiene el momento magnético correspondiente.

La presencia de ferromagnetismo superficial ha sido confirmada experimentalmente mediante microscopía de fuerza atómica (AFM) en un modo de gradiente de campo magnético. Por ejemplo, la Fig. 2 muestra las imágenes de superficie obtenidas para la muestra de KTaO ₃ nanocristalino . Las mediciones de microscopía de fuerza magnética (MFM) se realizaron con un microscopio de sonda de barrido Dimension 3000 NanoScope IIIa para mapear la variación espacial de la estructura de magnetización del componente fuera del plano del campo magnético disperso del KTaO ₃ superficie de la muestra. Los gradientes de fuerza magnética se midieron usando la técnica de dos pasadas (modo de elevación) donde se escaneó la topografía en la primera pasada en el modo de tapping y luego se mapearon los gradientes de campo magnético en la segunda utilizando el cambio de frecuencia de oscilación de la sonda moviéndose sobre la superficie (elevación la altura fue de 300 nm). Las sondas de fuerza magnética Veeco recubiertas de cobalto (MESP) con coercitividad de ~ 400 Oe, momento magnético de 1 · 10 ⁻¹³ Se utilizaron emu y un radio de vértice de la punta nominal de 25 nm. Antes de las mediciones, la sonda se magnetizó con un potente imán permanente con el campo alineado a lo largo del eje vertical de la punta.

Imágenes de superficie con regiones magnetizadas en KTaO ₃ nanocristales. un Mapeo de gradiente de campo magnético y b imagen de relieve superficial

Además, los bucles de magnetización estática se han obtenido experimentalmente a dos temperaturas para cada compuesto, a 290 y 150 K para KTaO ₃ ya 290 y 110 K para KNbO ₃ . Las curvas de magnetización experimentales se describen mediante la fórmula:

$$ M \ approx {M} _S {\ tanh} ^ {- 1} \ left (\ frac {H {V} _0 {M} _S} {k_B T} \ right) - \ frac {k_B T} {H {V} _0} $$ (1)

Aquí, M _S es la magnetización de saturación, H es un campo magnético estático, y V ₀ es el volumen de un cúmulo magnético infinito (de hecho, cerrado sobre una superficie de nanopartículas). La magnetización por saturación se definió de acuerdo con la fórmula (7) de [20]:

$$ {M} _S =\ left | {S} _1 {N} _1- {S} _2 {N} _2 \ right | $$ (2)

donde S ₁ y S ₂ son V (O) y Fe ³⁺ momentos magnéticos (giros de V (O) y Fe ³⁺ son 1/2 y 5/2, respectivamente), N ₁ y N ₂ son los números de V (O) y Fe, respectivamente. Valores dados N ₂ corresponden a las concentraciones de 0,06% en moles para KTO y 0,008% en moles de KNO obtenidas del análisis elemental, valores N ₁ se determinaron en consecuencia. Los resultados del ajuste se muestran en la Fig. 3. Para una descripción de los bucles de histéresis en campos magnéticos bajos, usamos el desplazamiento de la fórmula (2) en el valor del campo coercitivo, H _c . Los parámetros para cada curva se dan en la Tabla 1.

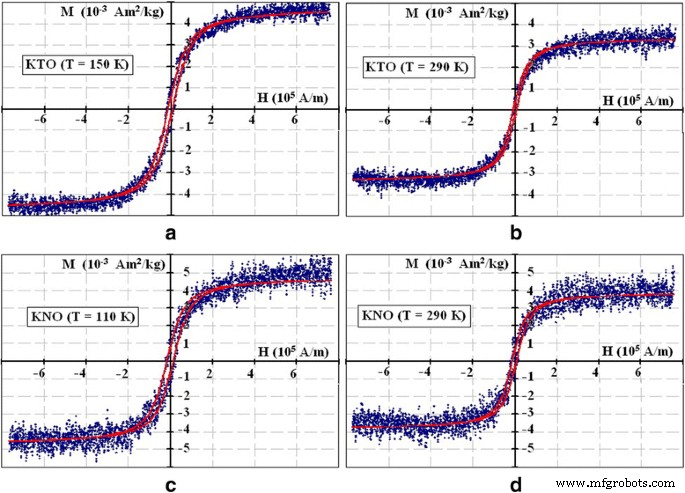
Curvas de magnetización estática. Curvas de magnetización en KTaO ₃ ( a , b ) y KNbO ₃ ( c , d ) nanopartículas en T =150, 290, 110 y 290 K. Los parámetros de ajuste se enumeran en la Tabla 1

Según el número de espines magnéticos estimado a partir de los datos de EPR [10, 15], la relación porcentual entre los subsistemas paramagnético y ferromagnético es de 14/86 en el tantalato de potasio de tamaño nanométrico y de 40/60 para el niobato de potasio. El mayor número de centros paramagnéticos en el niobato de potasio se debe a la presencia de impureza de manganeso incontrolada además de la impureza de hierro. Tenga en cuenta que el número de espines magnéticos que forman el subsistema ferromagnético, obtenido de experimentos anteriores, no es suficiente para establecer un orden magnético de largo alcance en todo el volumen de las nanopartículas. Por lo tanto, asumimos que la principal contribución al ferromagnetismo son los espines magnéticos, que se encuentran cerca de la superficie de las partículas, es decir, en la capa sub-superficial enriquecida por defectos. Como se indica en [24], la capa superficial enriquecida por defectos polares tiene un espesor constante de aproximadamente 10 celosías. Por otro lado, los autores de la Ref. [25] sugieren que la capa enriquecida por defectos magnéticos en un cristal semi-infinito tiene un espesor constante de 1 celosía. Dado que los complejos Fe ³⁺ -V (O) son defectos polares y magnéticos, suponemos que la capa de defecto cerca de la superficie tiene 5 constantes de celosía en nuestros cálculos. En KTaO ₃ y KNbO ₃ , la capa corresponde a 2 nm. Para utilizar las condiciones de percolación derivadas del artículo [17], asumimos que la distribución de defectos es uniforme en la capa cercana a la superficie. De acuerdo con los datos de microscopía electrónica de transmisión (TEM) (Fig. 4, ver también Fig. 1 en Ref. [9] y Fig. 2 en Ref. [26]), la forma de КTaO ₃ y KNbO ₃ Las nanopartículas se pueden modelar mediante un cubo. La distribución de tamaño de los cristalitos en cada compuesto obtenido a partir de los datos de TEM se presenta en la Fig. 5.

Imagen TEM del KTaO ₃ nanopartículas

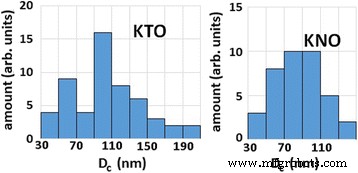
La distribución de tamaño de cristalitos en KTaO ₃ y KNbO ₃

Con base en las curvas de magnetización obtenidas experimentalmente, particularmente teniendo en cuenta los números dados de V (O) y Fe (ver Tabla 1), notamos el papel dominante de las vacantes de oxígeno en la magnetización. En esta suposición, una interacción de intercambio puede ser iniciada por electrones atrapados en vacantes de oxígeno y mediada por iones de impureza magnética Fe. Esta interacción se ha considerado en el modelo de polarones magnéticos ligados. Este modelo fue propuesto por primera vez por los autores de [22] para describir la aparición de ferromagnetismo en semiconductores magnéticos diluidos. En forma esquemática, nuestro modelo se presenta en la Fig. 6.

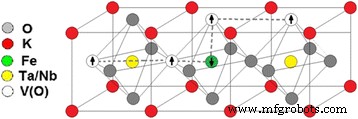
Modelo de orden magnético de largo alcance entre electrones atrapados en vacantes de oxígeno en el KTaO no estequiométrico ₃ / KNbO ₃ compuesto

Modelado teórico dentro del enfoque de filtración

Para determinar la concentración crítica de defectos totales, que pueden conducir a la formación de polarones magnéticos, utilizamos un enfoque de percolación. Utilizando los criterios de la teoría de la percolación, se mostró en el trabajo [17] cómo se establece matemáticamente el umbral de percolación del orden magnético de largo alcance. Omitiendo los detalles de los enfoques y principios de la Ref. [17], nos centraremos en las características utilizadas en nuestros cálculos y describiremos el curso general del cálculo.

De acuerdo con los datos TEM (ver Fig.4), se considera KTaO ₃ y KNbO ₃ Las nanopartículas se pueden modelar mediante un cubo. Se utilizó la red cúbica con una constante de red de 0,4 nm. En la capa cercana a la superficie de 2 nm de espesor (es decir, 5 celdas unitarias) (el fondo se da arriba, ver también las Refs. [24] y [25]) con defectos distribuidos aleatoriamente, átomos de Fe y vacantes de oxígeno V (O), teniendo en cuenta que la distribución de los átomos de hierro es uniforme. Según los modelos de centros axiales y rómbicos (ver Fig.1), la presencia de un átomo de Fe en el centro de la celda unitaria (cuando sustituye a los átomos de Nb o Ta en el KTaO ₃ o KNbO ₃ celosía) se acompaña de la aparición de V (O) en los bordes de la celda. Con cierta probabilidad, puede ocurrir una vacante de oxígeno V (O) o dos vacantes 2 V (O). La probabilidad es del 50% en nuestro caso que corresponde a la relación determinada experimentalmente de los centros axiales (Fe-V (O)) y rómbicos (Fe-2 V (O)) en KTaO ₃ y KNbO ₃ [9, 10, 15]. Los defectos fueron modelados por esferas en nuestros cálculos, en los que los radios de vacancia de iones de hierro y oxígeno son r (Fe ³⁺ ) =0.064 nm y r (V (O)) =0,132 nm, respectivamente. La distancia d entre los defectos se definió como la distancia entre la superficie de las esferas y no entre sus centros. Conociendo las coordenadas de los defectos aleatorios, es decir, átomos de Fe y vacantes V (O), calculamos la distancia d entre ellos. El resultado de la distribución de defectos se muestra esquemáticamente en la Fig. 7.

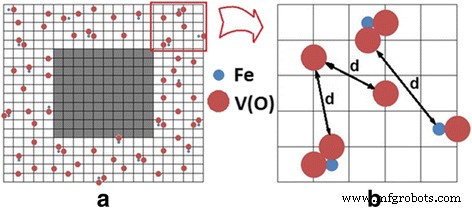
Distribución de defectos en la capa superficial. un Área de luz muestra la capa de defecto debajo de la superficie. Área gris refleja la profundidad de las nanopartículas, donde los defectos están casi ausentes en comparación con la capa subsuperficial. La proporcionalidad entre el tamaño del área del defecto debajo de la superficie y el núcleo interno libre de defectos se rompe en esta figura para una representación más clara de la distribución de defectos en la capa debajo de la superficie. Los átomos de Fe se distribuyen uniformemente en la profundidad de la capa del defecto, las vacantes de oxígeno V (O) se encuentran cerca de los átomos de Fe. b Zoom de la capa defectuosa ( a ); d es la distancia entre defectos

De acuerdo con la teoría de la percolación, el orden magnético de largo alcance en el sistema ocurre tan pronto como se forma el cúmulo infinito (ver, por ejemplo, p.235 en Ref. [17]). La distancia entre los defectos, que forman un cúmulo infinito y, por tanto, cumplen la condición de percolación ("umbral de percolación"), se define como un radio de percolación, R _perc . Para determinar el radio de percolación, se realizó el cálculo para las nanopartículas de diferentes tamaños, para asegurar que la condición de percolación se cumple realmente. Para el caso, la relación entre el número de defectos magnéticos en el cúmulo infinito y el número total de defectos magnéticos en el sistema permanece sin cambios en partículas de diferentes tamaños. El tamaño de las nanopartículas es D × D × D celdas unitarias, donde D =20, 30, 40. Para determinar la dependencia del radio de percolación de la concentración de defectos magnéticos, se realizaron los cálculos para las concentraciones presentadas en la Tabla 2. Aquí, n ₁ define la concentración de las vacantes de oxígeno que no se encuentran cerca de los átomos de Fe, n ₂ es la concentración de átomos de Fe, y n es una concentración total de defectos. Tenga en cuenta que realizamos cálculos para dos casos. Para el caso I, n ₁ / n ₂ =Const y n varía. Para el caso II, n ₂ =Const y n ₁ varía.

Para determinar el radio de percolación R _perc , utilizamos el siguiente procedimiento. Para cada concentración, establecemos un cierto valor R que se varió de 0,1 a 5,9 nm con un incremento de 0,2 nm. La distancia d entre los defectos se comparó con el valor R (para cada R valor). Por tanto, todos los defectos magnéticos se dividen en dos grupos. Si la distancia d _ij entre el i más cercano th y j th defectos es menor o igual a la R , es decir, d _ij ≤ R , clasificamos estos defectos en un grupo, en el que existe un acoplamiento magnético entre los defectos; de lo contrario, si d _ij > R , referimos tales defectos al otro grupo, donde el acoplamiento entre defectos está ausente (es decir, roto). Como resultado del cálculo, obtenemos la matriz de m × m , qué elementos son valores booleanos 1/0 (presencia / ausencia de acoplamiento entre i th y j th defectos). Aquí, m es el número de defectos en el área subsuperficial en la partícula de cierto tamaño. A continuación, utilizando el principio de las cadenas de Markov, encontramos los grupos magnéticos (es decir, agregados de puntos {Fe, V (O)}), que interactúan indirectamente. Para ello, planteamos el mencionado m × m matriz a la potencia m y obtén una nueva matriz m × m , qué elementos son valores booleanos 1/0 (presencia / ausencia de interacción mediada entre i th y j th defectos). La suma máxima de la línea de la matriz corresponde al tamaño del grupo más grande para un tamaño de partícula dado. Se realizaron cálculos similares para cada valor de R y el tamaño de las nanopartículas. Resultados obtenidos para una concentración n =0,6117 nm ⁻³ se enumeran en la Tabla 3. El área en cursiva de la tabla corresponde a la R = R _perc valor que es el radio de percolación R _perc =1,7 nm. Radio de filtración R _perc se encontró de acuerdo con el umbral de percolación descrito anteriormente.

La Figura 8 muestra esquemáticamente la formación del cúmulo infinito en las partículas de diferentes tamaños.

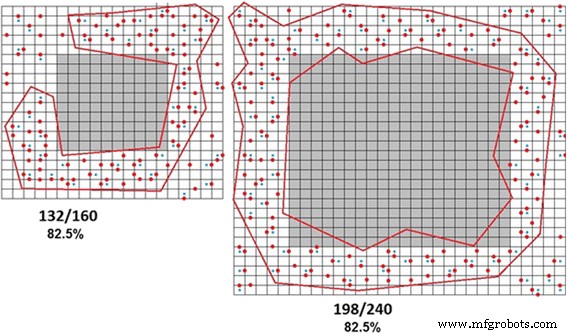
Formación de racimos infinitos en las partículas de diferente tamaño. El umbral de percolación es del 82,5%, definido como el porcentaje de defectos en el racimo que no depende del tamaño de las partículas, como se anticipó

Resultados y discusión

La figura 9a muestra la dependencia del radio de percolación R _perc sobre la concentración de defectos para el caso I, es decir, cuando n ₁ / n ₂ =Const y n varía. Las curvas sólidas se trazan usando la fórmula

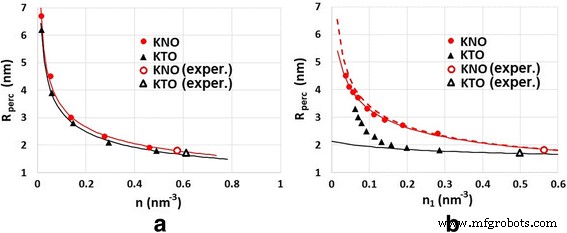
Radio de percolación versus concentración de defectos en dos casos: a n ₁ / n ₂ =Constante, n varía y b n ₂ =Constante, n ₁ varía. Los puntos se calculan numéricamente en el marco de nuestro modelo, las curvas sólidas se basan en la fórmula (1). Los puntos marcados con etiquetas corresponden a los materiales estudiados (KTaO ₃ y KNbO ₃ )

$$ {R} _ {\ mathrm {perc}} =\ frac {a} {\ sqrt [3] {n}} - b $$ (3)

con parámetros a =1.6 y 1.7 para KTO y KNO, respectivamente, y b =0,25 nm para ambos, KTO y KNO. El primer término de la fórmula (3) es coherente con la ecuación (4) de la Ref. [20] para un radio de percolación, \ ({R} _ {\ mathrm {perc}} =\ frac {a} {\ sqrt [3] {n}}. \)

El valor de R _perc es un cierto valor crítico, para R > R _perc , se formará el cúmulo infinito, que está dentro de la condición necesaria de aparición del orden magnético de largo alcance en el marco de la teoría de la percolación. Asumimos que el radio R _perc es igual para los pares Fe-Fe, V (O) -V (O) y V (O) -Fe. Sin embargo, según los resultados calculados y los hechos experimentales, podemos afirmar que el radio R _perc no puede ser inferior a 1,6 nm para KTaO ₃ y 1,7 nm para KNbO ₃ .

Consideremos la fórmula (3) con más detalle. El significado físico de la expresión \ (1 / \ sqrt [3] {n} \) es la distancia entre los defectos que participan en el intercambio magnético para la aparición de un orden de largo alcance. El valor a puede ser tanto menor como mayor que 1. Cuando el radio R _perc corresponde a la distancia media entre defectos, el valor a =1, por lo que \ ({R} _ {\ mathrm {perc}} =1 / \ sqrt [3] {n} \). Cuando el número de acoplamientos magnéticos aleatorios, que se forman por la interacción entre defectos a una distancia menor que la media, es suficiente para la formación de un cúmulo infinito, valor a es menor que 1. Por ejemplo, a =0,86 en el trabajo [17]. Resulta que la R _perc es 1,6-1,7 veces mayor que la distancia media entre defectos en nuestro caso. Esto se puede explicar de la siguiente manera.

El valor de la distancia media entre defectos tiene sentido para una distribución uniforme de defectos en la capa subsuperficial. La distribución de los átomos de Fe se considera casi uniforme, pero teniendo en cuenta que los átomos de Fe están colocados en el centro de la celda, sus posiciones son coordenadas espaciales discretas, lo que también afecta el valor a en la ecuación 3, y la ubicación de las vacantes de oxígeno V (O) no es uniforme porque siempre están cerca de los átomos de Fe (véase la figura 6). Por tanto, la distancia entre los átomos de Fe es mucho mayor que la distancia entre el átomo de Fe y la vacante de oxígeno V (O). Por lo tanto, el radio R _perc en realidad no depende de la distancia promedio entre todos los defectos, pero depende de la distancia promedio entre defectos en diferentes celdas unitarias (esta puede ser la distancia entre Fe-Fe, V (O) -V (O), V (O ) -Fe). La presencia de vacantes de oxígeno cerca de los átomos de Fe reduce ligeramente la distancia entre las células defectuosas debido a la pequeñez de la distancia V (O) -Fe en comparación con la distancia Fe-Fe. Eso significa que en este caso, en realidad estamos tratando con la distancia promedio entre átomos de Fe.

Resta del segundo componente b =0.25 nm en la ecuación (3) se puede explicar de la siguiente manera. Normalmente, la distancia entre defectos en esta ecuación se define como la distancia entre los centros de defectos, si un defecto se simula como un punto. En nuestros cálculos, R _perc se define como la distancia entre las superficies de la esfera en la que colocamos el defecto o defectos. Entonces, el valor R _perc , estimada como la distancia entre las superficies de las esferas, es diferente de la R _perc estimada como la distancia entre los centros al menos en la suma de dos radios de defectos que interactúan. La suma puede variar de 0,128 nm para la interacción Fe-Fe (Fig. 10a) a 0,264 nm para la interacción V (O) -V (O) (Fig. 10c). Además, dado que la distancia entre el átomo de Fe y la vacante más cercana V (O) es mucho menor que la calculada, necesaria para establecer un acoplamiento entre defectos, en ciertos casos, R _perc se puede definir como la distancia V (O) -Fe o V (O) -V (O) de diferentes celdas (ver Fig. 10b, c). Cuando aumenta el número de V (O), el número de casos presentados en la Fig. 10b, c también aumenta, respectivamente. En consecuencia, el valor calculado de b = 0.25 nm indica que principalmente se produce una interacción de intercambio directamente entre los electrones atrapados en las vacantes de oxígeno.

Reducción de R _perc para la interacción entre diferentes defectos ( a - c ) en comparación con una distribución uniforme de Fe ( azul ) átomos es causada por la presencia de vacantes de oxígeno V (O) ( rojo )

La Figura 9b muestra la dependencia del radio de percolación R _perc sobre la concentración de defectos para el caso II, es decir, cuando n ₂ =Const y n ₁ varía. Aquí, la influencia de los átomos de Fe aumenta a medida que n ₁ disminuye. Esto es más pronunciado para KTO (curva sólida negra en la Fig. 9b). Sin embargo, intentamos ajustar los datos calculados usando la fórmula (3) con los parámetros a =0.66 y b =0,15 nm. El valor de b indica que la cantidad relativa de interacciones directas V (O) -V (O) disminuye, mientras que la cantidad de interacciones indirectas a través de átomos de Fe aumenta.

Conclusiones

Consideramos el mecanismo microscópico que conduce al surgimiento del ordenamiento ferromagnético en KTaO ₃ ferroeléctrico y KNbO ₃ nanopartículas. Nuestro enfoque se basa en la teoría de la percolación magnética. Describe la formación de polarones magnéticos superficiales en los que se produce una interacción de intercambio entre los portadores de carga, es decir, los electrones, atrapados en las vacantes de oxígeno, directa o indirectamente a través de átomos magnéticos de Fe.

La dependencia del radio R _perc sobre la concentración total n de defectos a n constante ₁ / n ₂ proporción ( n ₁ es la concentración de vacantes de oxígeno y n ₂ es la concentración de átomos de Fe) se determina en el marco de la teoría de la percolación. Apareció que la dependencia está bien descrita por la fórmula \ ({R} _ {\ mathrm {perc}} =\ frac {a} {\ sqrt [3] {n}} - b \), donde los valores de parámetros a =1.6 y 1.7 para KTO y KNO, respectivamente, y b =0,25 nm para ambos, KTO y KNO. Se ha descubierto que el radio de percolación magnética real no puede ser inferior a 1,6 nm para KTaO ₃ y 1,7 nm para KNbO ₃ .

Utilizando la concentración crítica calculada de defectos magnéticos, los bucles de histéresis magnética medidos experimentalmente se describen bien mediante dos fórmulas de tipo Langeven desplazadas. Valor de saturación de magnetización M _S depende de los momentos magnéticos de las vacantes de oxígeno V (O) y Fe ³⁺ iones y sus cantidades N ₁ y N ₂ , respectivamente, en el grupo infinito como M _S =| S ₁ N ₁ - S ₂ N ₂ |, que está en completo acuerdo con la Ref. [20].

Los cálculos teóricos describen adecuadamente los resultados experimentales obtenidos en KTaO ferroeléctrico ₃ y KNbO ₃ nanopartículas sintetizadas por oxidación de tantalio metálico en nitrato de potasio fundido con la adición de hidróxido de potasio, que exhiben un ferromagnetismo débil, mientras que estos compuestos no son magnéticos a granel.

Abreviaturas

AFM:

Microscopía de fuerza atómica

MESP:

Sondas de fuerza magnética recubiertas de cobalto

MFM:

Microscopía de fuerza magnética

TEM:

Microscopía electrónica de transmisión

Influencia de las condiciones de la formación de nanomateriales de Pd / SnO2 en las propiedades de los sensores de hidrógeno Compuesto híbrido Nanoestructurado de sílice / oro-celulosa-Amino-POSS mediante el proceso Sol-Gel y sus propiedades