La bifurcación de susceptibilidad magnética en el aislante topológico Sb2Te3 dopado con Ni con orden antiferromagnético acompañado de una alineación ferromagnética débil
Resumen
La susceptibilidad magnética revela una discontinuidad a la temperatura de Néel y se observó un bucle de histéresis con un campo coercitivo bajo por debajo de la temperatura de Néel. La susceptibilidad magnética de los procesos de enfriamiento de campo cero y enfriamiento de campo coinciden a una temperatura por encima de la discontinuidad, y se dividen a la temperatura de la discontinuidad. La división de la susceptibilidad magnética es mayor en campos magnéticos externos más bajos. No se observó más división de susceptibilidad magnética en un campo magnético por encima de 7000 Oe que es consistente con la energía de anisotropía magnética. Nuestro estudio respalda que estas características de susceptibilidad magnética se originan a partir de un orden antiferromagnético acompañado de un ferromagnetismo débil.
Introducción
Los aislantes topológicos tridimensionales poseen un estado de superficie sin espacios de dispersión lineal que está protegido por simetría de inversión del tiempo [1, 2]. El estado de la superficie topológica consiste en fermiones de Dirac filtrados por espín. Esta textura helicoidal de giro del estado de la superficie topológica ha atraído una gran atención debido a sus posibles aplicaciones eléctricas y relacionadas con el giro [3,4,5,6,7,8,9,10,11,12,13,14 , 15,16,17,18,19,20]. Aparte de las características exóticas intrínsecas, la introducción de magnetización en el aislante topológico modificará la electrónica. Esta interacción de intercambio entre el electrón de conducción y los átomos magnéticos rompe la simetría de inversión del tiempo y abre una brecha en el estado de la superficie de Dirac. El fermión de Dirac en el estado de superficie se vuelve masivo [1, 2, 21] y conduce a muchas propiedades interesantes, como el efecto Hall anómalo cuántico, [22, 23] efecto magnetoeléctrico topológico [24], sintonización del modo de borde quiral [ 25, 26] y trenzado Majorana [27,28,29]. El portador del estado de la superficie topológica domina estas propiedades magnetoeléctricas. Se realizaron muchos trabajos experimentales en películas delgadas de Mn, Cr y V (Bi, Sb) \ (_ {2} \) Te \ (_ {3} \) para realizar la predicción teórica [30]. La mayoría de estos estudios se centraron principalmente en las propiedades de transporte eléctrico-magneto, como el efecto Hall anómalo cuántico, el efecto magnetoeléctrico topológico y aplicaciones relacionadas. Debido a la señal de magnetismo débil en una película delgada con un aislante topológico dopado con elemento magnético débil, se informaron estudios raros sobre las propiedades magnéticas intrínsecas del dopado con imán en aisladores topológicos dopados con elemento magnético y el acoplamiento magnético relacionado no está bien explorado. Para comprender las nuevas propiedades físicas intrínsecas del aislante topológico dopado con elemento magnético, especialmente el papel del elemento magnético y el acoplamiento de interacción magnética relacionado, podría ser útil utilizar con precisión las propiedades del magneto en la aplicación relacionada.
En este trabajo, estudiamos las propiedades magnéticas del monocristal de aislante topológico Sb \ (_ {2} \) Te \ (_ {3} \) dopado con Ni. Se observó un bucle de histéresis con un campo coercitivo bajo por debajo de la temperatura de Néel (\ (T _ {\ mathrm {N}} \)). La susceptibilidad magnética revela una patada en \ (T _ {\ mathrm {N}} \) que es independiente del campo magnético externo. La susceptibilidad magnética de los procesos de enfriamiento de campo cero y enfriamiento de campo coinciden por encima de \ (T _ {\ mathrm {N}} \), y están bifurcados por debajo de \ (T _ {\ mathrm {N}} \). La división de la susceptibilidad magnética es mayor a temperaturas y campos magnéticos externos más bajos. No se observa más división de susceptibilidad magnética en un campo magnético por encima de 7000 Oe. Nuestro estudio apoya que estas características de susceptibilidad magnética se originan en un orden antiferromagnético acompañado de ferromagnetismo débil. La susceptibilidad saturada extraída va bien con la tendencia de la cúspide de susceptibilidad magnética medida. Aparte de la mayoría de los informes de que la cúspide de susceptibilidad magnética se origina en la textura del espín del portador en el punto de Dirac del estado de la superficie topológica, nuestros resultados revelan que podría estar relacionada con el ferromagnetismo de los elementos magnéticos.
Método experimental
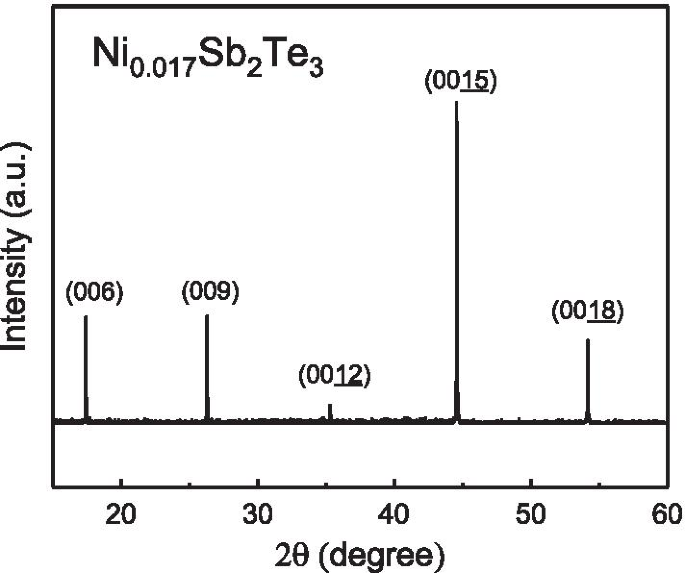
El espectro XRD del monocristal de Ni \ (_ {0.016} \) Sb \ (_ {2} \) Te \ (_ {3} \). Revela picos afilados y eso apoya la estructura altamente monocristalizada
Se cultivaron monocristales de Sb \ (_ {2} \) Te \ (_ {3} \) con un horno de zona flotante calentado por resistencia (RHFZ) hecho en casa. Las materias primas de partida de Sb \ (_ {2} \) Te \ (_ {3} \) se mezclaron de acuerdo con la relación estequiométrica. Al principio, las mezclas estequiométricas de elementos de alta pureza Ni (99,995%), Sb (99,995%) y Te (99,995%) se fundieron a \ (700 \ sim 800 ^ {\ circ} \) C durante 20 h y luego lentamente enfriado a temperatura ambiente en un tubo de vidrio de cuarzo al vacío. El material se utilizó como varilla de alimentación para el siguiente experimento RHFZ. Nuestro trabajo anterior respalda que se puede obtener una uniformidad cristalina extremadamente alta en cristales aislantes topológicos a través del método RHFZ. Después del crecimiento, los cristales se enfriaron en un horno a temperatura ambiente. Los cristales recién desarrollados se escindieron a lo largo del plano basal, con una superficie similar a un espejo plateado y brillante, y luego se prepararon para experimentos adicionales. Los resultados del espectro de energía dispersiva (EDS) apoyan que \ (\ mathrm {Ni}:\ mathrm {Sb}:\ mathrm {Te} =0.017:2:3 \). La figura 1 muestra el espectro de difracción de rayos X (XRD). Revela picos agudos y estos picos son consistentes con la base de datos de Sb \ (_ {2} \) Te \ (_ {3} \). Esto confirma que nuestra muestra está altamente cristalizada. Se espera que los átomos de Ni se distribuyan de manera uniforme y aleatoria en el monocristal. El tamaño del cristal es de 3 mm de largo, 2 mm de ancho y 0,42 mm de espesor. Las medidas de magnetismo se realizaron utilizando la técnica estándar en un aparato comercial (Quantum Design MPMS) con un campo magnético de hasta 7 T. El campo magnético se aplicó perpendicular a la gran superficie dividida.
Resultados y discusión
La Figura 2 muestra la magnetización en función de campos magnéticos a diferentes temperaturas, y reveló la característica diamagnética en una amplia gama de campos magnéticos y temperaturas. Este diamagnetismo proviene del espín del portador y es consistente con los informes anteriores en aislantes topológicos BSTS [31]. Como se muestra en el recuadro superior derecho, a diferencia de los informes anteriores, se observó un bucle de histéresis a temperaturas inferiores a 125 K. El campo coercitivo del bucle de histéresis muestra una dependencia de la temperatura débil y es de aproximadamente 50 Oe. La magnetización remanente y saturada del bucle de histéresis es de aproximadamente \ (10 ^ {- 5} \) emu / gy \ (10 ^ {- 4} \) emu / ga 100 K. El campo coercitivo bajo, el pequeño remanente , y la pequeña magnetización saturada indica ferromagnetismo débil. Como se muestra en el recuadro inferior izquierdo, no se observaron bucles de histéresis claros a temperaturas superiores a 125 K. El ferromagnetismo se origina a partir de los momentos magnéticos alineados de los elementos magnéticos. La energía térmica podría aleatorizar el momento magnético alineado y difuminar el ferromagnetismo por encima de una temperatura crítica. Nuestra observación indica que el sistema revela una transición de ferromagnetismo débil alrededor de 120 K.
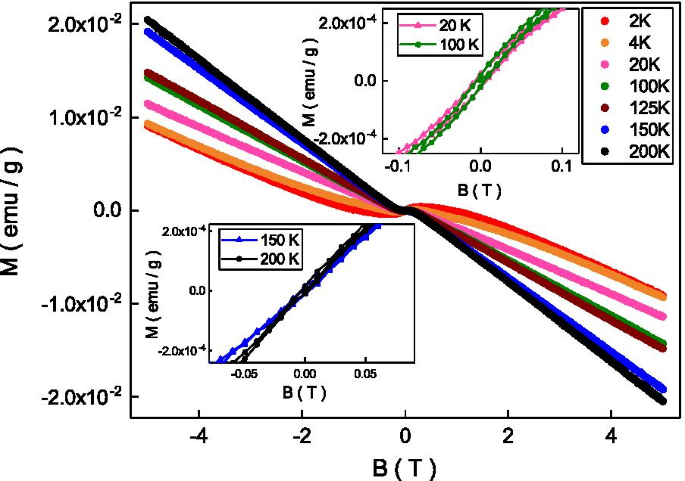
La susceptibilidad en función de campos magnéticos de 2 a 200 K. Revela el diamagnetismo en campos magnéticos elevados. Recuadro superior derecho:el bucle de histéresis se observó a una temperatura inferior a 125 K Recuadro inferior izquierdo:No se observó ningún bucle de histéresis a una temperatura superior a 125 K
Para investigar la característica del magnetismo intrínseco de la transición ferromagnética débil observada, la susceptibilidad magnética dependiente de la temperatura se realizó mediante procesos de enfriamiento de campo y de enfriamiento de campo cero. La Figura 3 muestra la susceptibilidad magnética de los procesos refrigerados por campo y por campo cero en diferentes campos magnéticos externos. La susceptibilidad magnética aumenta a medida que disminuye la temperatura. Revela una discontinuidad en 125 K (\ (T _ {\ mathrm {N}} \)) y \ (T _ {\ mathrm {N}} \) es independiente de los campos magnéticos externos. \ (T _ {\ mathrm {N}} \) es la temperatura de Néel y el mecanismo detallado se discutirá y aclarará a continuación. La susceptibilidad magnética de enfriado por campo y enfriado por campo cero coincide arriba de \ (T _ {\ mathrm {N}} \) y se bifurca debajo de \ (T _ {\ mathrm {N}} \). Se observa una división de susceptibilidad magnética más grande en campos magnéticos externos más bajos. Nuestro resultado experimental muestra que esta discontinuidad y la división de la susceptibilidad magnética ya no se observa en un campo magnético superior a 7000 Oe. Es digno de notar que la fluctuación de la señal en el campo magnético de 50 Oe es obviamente mayor que la de otros campos magnéticos. Una de las posibles razones es que la alineación del momento magnético es metaestable en el 50 Oe que está cerca del campo coercitivo del bucle de histéresis. Como se muestra en la Fig. 2, el bucle de histéresis solo se observó por debajo de 125 K, que es la misma que la temperatura crítica de la bifurcación de susceptibilidad magnética en la Fig. 3. Esto indica que la división de susceptibilidad magnética observada podría estar relacionada con el ferromagnético débil debajo del \ (T _ {\ mathrm {N}} \). Se sabe que el efecto ferromagnético se difuminaría por la energía térmica y la susceptibilidad magnética por encima de la temperatura crítica podría describirse mediante la ley de Curie-Weiss, \ (\ chi =\ chi _ {0} + \ frac {C} { T- \ theta} \), donde \ (\ chi \) es la susceptibilidad magnética medida, \ (\ chi _ {0} \) es la susceptibilidad magnética a 0 K, C es la constante de Curie que corresponde al magneton de Bohr, T es la temperatura y \ (\ theta \) es la temperatura de Curie [32]. El recuadro de la Fig. 4 muestra la dependencia de la temperatura de \ (\ frac {1} {\ chi - \ chi _ {0}} \) refrigerado por campo cero en diferentes campos magnéticos externos. El \ (\ frac {1} {\ chi - \ chi _ {0}} \) es proporcional a una temperatura entre 125 y 250 K, y la pendiente es mayor en campos magnéticos externos más bajos. La pendiente está relacionada con la constante de Curie. La extrapolación lineal de \ (\ frac {1} {\ chi - \ chi _ {0}} \) entre 125 y 250 K de todos los campos magnéticos externos coincide en -125 K. Siguiendo la ley de Curie-Weiss, este valor corresponde a \ (\ theta \). El \ (\ theta \) (-125 K) negativo indica que es un sistema antiferromagnético por debajo de \ (T _ {\ mathrm {N}} \) y \ (T _ {\ mathrm {N}} \) se conoce como Temperatura de Néel [33]. El valor absoluto de \ (\ theta \) es consistente con el \ (T _ {\ mathrm {N}} \) observado en la Fig. 3, y la temperatura crítica para observar el ciclo de histéresis (125 K) en la Fig. 2 Estas observaciones indican que el ferromagnetismo débil y el antiferromagnetismo coexisten debajo de \ (T _ {\ mathrm {N}} \).
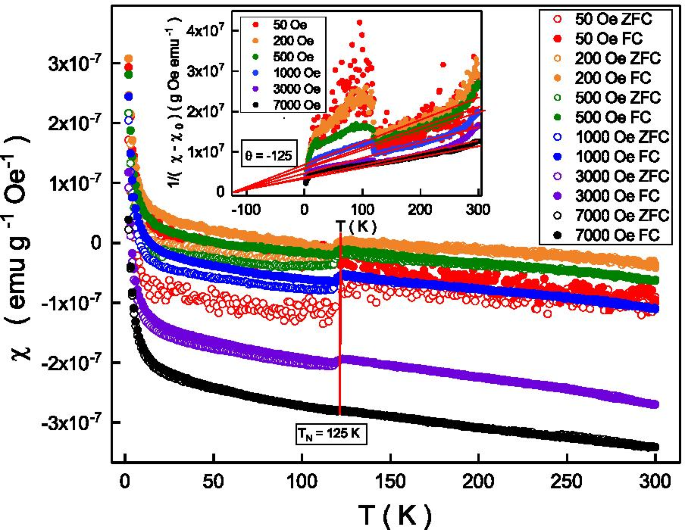
La susceptibilidad magnética de los procesos de enfriamiento de campo y de campo cero en diferentes campos magnéticos externos. La susceptibilidad magnética del campo enfriado y enfriado por campo cero coincide por encima de 125 K y se bifurca por debajo de 125 K. Una mayor susceptibilidad magnética se divide a temperaturas y campos magnéticos externos más bajos. No se observa más división de susceptibilidad magnética en un campo magnético por encima de 7000 Oe. Recuadro superior derecho:la susceptibilidad magnética sigue la ley de Curie-Weiss
Como se muestra en el recuadro de la Fig.3, la constante de Curie, C , es más grande en campos magnéticos más altos. Siguiendo la función paramagnética de Langevin, C podría expresarse como \ (C =\ frac {N \ mu _ {0} \ mu ^ {2}} {3k _ {\ mathrm {B}} T} \) donde N es el número de elementos magnéticos por unidad de gramo, \ (\ mu \) es el momento efectivo de un elemento magnético, \ (\ mu _ {0} \) es la permeabilidad al vacío y \ (k _ {\ mathrm {B}} \) es la constante de Boltzmann [34]. El \ (\ mu \) estimado en 200 Oe es aproximadamente 3,5 \ (\ mu _ {\ mathrm {B}} \) que se cierra al valor teórico de 3,32 \ (\ mu _ {\ mathrm {B}} \ ) [35]. Esto confirma que el comportamiento del magnetismo podría explicarse por la ley de Curie-Weiss.
El momento magnético se congela aleatoriamente en el campo cero frío y se congela a lo largo de la dirección del campo magnético externo en el campo frío. La bifurcación de susceptibilidad magnética se origina a partir de la anisotropía magnética. Esta característica podría ser una característica de un orden de antiferromagnetismo acompañado de ferromagnetismo débil; Los momentos ferromagnéticos de los dominios se congelan en una dirección aleatoria en campo cero frío, mientras que se ven obligados a alinearse a lo largo del campo magnético aplicado al enfriarse a través de \ (T _ {\ mathrm {N}} \) en campo frío [36]. Como se discutió anteriormente, se compone de características ferromagnéticas y antiferromagnéticas débiles debajo de \ (T _ {\ mathrm {N}} \) en nuestro sistema. La alineación ferromagnética débil rompería ligeramente el orden de antiferromagnetismo e induciría la anisotropía magnética. La bifurcación de susceptibilidad magnética podría entenderse como ferromagnetismo débil en un sistema antiferromagnético. Estos resultados apoyan que la bifurcación de susceptibilidad magnética observada por debajo de 125 K es la característica magnética del ferromagnetismo débil en un sistema antiferromagnético. La diferente susceptibilidad que se divide en diferentes campos magnéticos externos podría originarse a partir de los diferentes niveles de polarización parcial del antiferromagnetismo en los campos magnéticos externos.
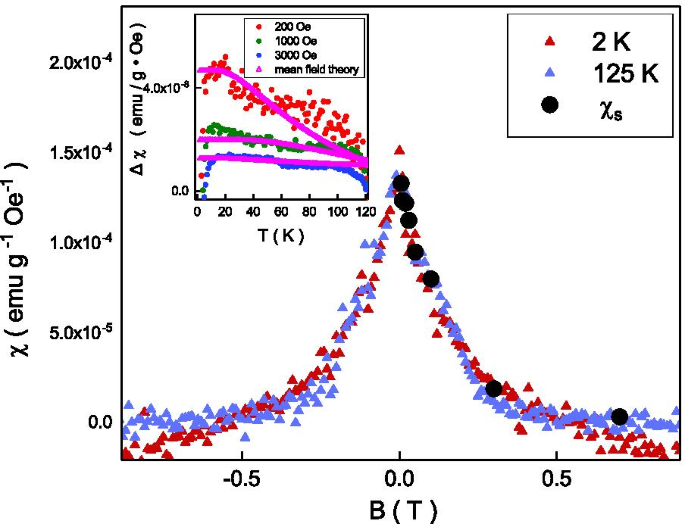
Recuadro superior izquierdo:la diferencia de susceptibilidad magnética de campo enfriado y enfriado por campo cero sigue la teoría del campo medio. La susceptibilidad saturada extraída va bien con la tendencia de la cúspide de susceptibilidad magnética medida
Siguiendo la teoría del campo medio, [37] el \ (T _ {\ mathrm {N}} \) está relacionado con la fuerza de acoplamiento de intercambio, \ (J_ {0} \), y podría expresarse como \ (T _ {\ mathrm {N}} =\ frac {S (S + 1)} {3k _ {\ mathrm {B}} T} J_ {0} \), donde S es el momento de giro, \ (k _ {\ mathrm {B}} \) es la constante de Boltzmann. El \ (J_ {0} \) iría a \ (4.28 \ times 10 ^ {22} \) joule en nuestro sistema con \ (T _ {\ mathrm {N}} \) =125 K. La teoría del campo medio es compatible que la magnetización está relacionada con la energía térmica por un factor de \ (e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). La susceptibilidad magnética podría expresarse como \ (\ chi =\ chi _ {\ mathrm {S}} (1-e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} ) \), donde \ (\ chi _ {\ mathrm {S}} \) es la susceptibilidad magnética saturada. La división de susceptibilidad magnética, \ (\ chi _ {\ mathrm {FC}} - \ chi _ {\ mathrm {ZFC}} \) podría expresarse como \ (\ chi _ {\ mathrm {S}} e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). El \ (\ chi _ {\ mathrm {S}} \) es sensible a los campos magnéticos externos. Como se muestra en el recuadro de la Fig. 4, esta ecuación podría explicar bien nuestro resultado experimental en una amplia gama de temperaturas y campos magnéticos externos. El \ (\ chi _ {\ mathrm {S}} \) es una función de campos magnéticos externos. Para examinar más a fondo el resultado, la susceptibilidad dependiente del campo magnético se realiza a temperaturas por debajo de \ (T _ {\ mathrm {N}} \), y muestra una cúspide en campos magnéticos cero. Esta cúspide de susceptibilidad magnética a un campo magnético cero se observa ampliamente en materiales topológicos, y se especula que se origina en la textura de espín alineado libre en el punto de Dirac [38]. La espectroscopia de fotoemisión resuelta en ángulo (ARPES) revela que el nivel de Fermi se encuentra por debajo del punto de Dirac en nuestro Sb \ (_ {2} \) Te \ (_ {3} \) [39]. La cúspide observada no debe tener su origen en la textura de giro en el punto de Dirac. Por otro lado, el campo coercitivo del bucle de histéresis es aproximadamente 50 Oe, que es dos órdenes de magnitud menor que el ancho total a la mitad del máximo de la cúspide, 0,4 T, y el bucle de histéresis no debe ser la fuente principal de la cúspide observada. . Como se muestra en el recuadro de la Fig. 4, el \ (\ chi _ {\ mathrm {S}} \) que depende del campo magnético extraído sigue la misma tendencia del campo magnético de la susceptibilidad magnética medida. Esto indica que la cúspide de susceptibilidad ampliamente observada podría originarse en el orden antiferromagnético acompañado de una alineación de ferromagnetismo débil.
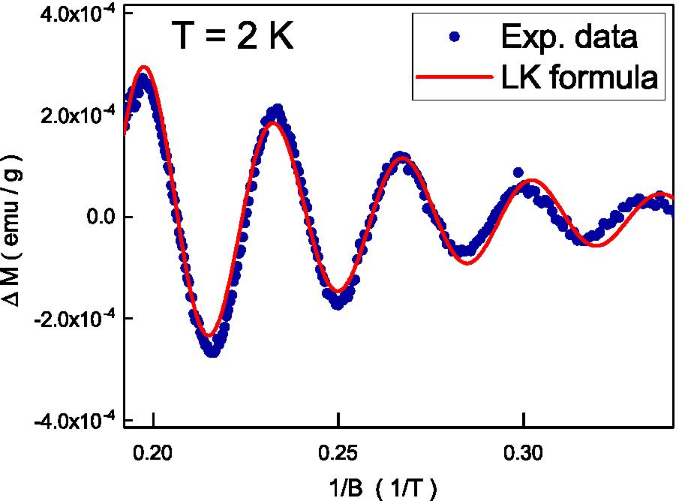
Las oscilaciones dHvA en función de campos magnéticos inversos. El resultado experimental encaja bien con la ecuación teórica
Tras el análisis, la bifurcación de susceptibilidad se origina en el magnetismo de orden de ferromagnetismo débil acompañado de antiferromagnetismo. La división de la susceptibilidad magnética está relacionada con la anisotropía magnetocristalina. A continuación, estimamos además la energía de anisotropía magnetocristalina, \ (\ Delta E =\ frac {M _ {\ mathrm {S}} H _ {\ mathrm {C}} V} {2} \), donde \ (H _ {\ mathrm {C}} =50 \) Oe, \ (M _ {\ mathrm {S}} =1.81 \ times 10 ^ {- 11} \) J / T y \ (V =2.5 \ times 10 ^ {- 9} \ ) m \ (^ {3} \) en nuestro sistema, y el \ (\ Delta E \ sim 1.13 \ times 10 ^ {22} \) Joule [40]. Siguiendo la energía del momento magnético, \ (g \ mu _ {\ mathrm {B}} B \), se podría estimar que la energía de anisotropía magnetocristalina será menor que la energía del momento magnético en \ (B> 0,61 \) T. Eso es consistente con nuestra observación de que la división de la susceptibilidad magnética ya no se observa en campos magnéticos externos por encima de 0,7 T.
La figura 5 muestra la susceptibilidad magnética en función de 1 / B y muestra oscilaciones periódicas. Esto se conoce como oscilaciones del efecto De Haas-Van Alphen (dHvA) que se originan en el movimiento orbital de un electrón itinerante en campos magnéticos elevados [41]. Analizamos las oscilaciones dHvA ajustando la magnetización oscilatoria a la fórmula de Lifshitz-Kosevich (LK) [42], \ (\ Delta M \ propto -R \ sin [2 \ pi (\ frac {F} {B} - \ delta _{pags})]\). R está relacionado con la tasa de dispersión de la portadora, el efecto Zeeman y el ensanchamiento del nivel de Landau [43]. La oscilación se describe mediante un término sinusoidal que contiene el factor de fase \ (\ delta _ {p} \). \ (\ delta _ {p} \) está relacionado con la fase Berry (\ (\ Phi _ {B} \)), \ (\ delta _ {p} =\ frac {1} {2} - \ frac { \ Phi _ {B}} {2 \ pi} \). La dimensión del bolsillo de Fermi caracteriza el valor \ (\ delta _ {p} \). Como se muestra en la Fig.5, la ecuación teórica encaja bien con nuestro resultado experimental y la \ (\ delta _ {p} =0.43 \) y \ (F =29.8 \) T extraídas. Eso es consistente con la predicción teórica y la El dHvA observado proviene del estado topológico de la superficie. Siguiendo la relación de Onsager [44], \ (F =\ frac {\ hbar K_F ^ {2}} {2 \ pi} \), se podría estimar que \ (K_ {F} =0.030 \) Å - 1 es consistente con el valor reportado por ARPES. Estos resultados sugieren que las oscilaciones dHvA se originan en el estado de la superficie topológica.
Conclusión
En este trabajo, estudiamos el comportamiento magnético de un monocristal de aislante topológico Sb \ (_ {2} \) Te \ (_ {3} \) dopado con Ni. Se observó un bucle de histéresis con un campo coercitivo bajo por debajo de la temperatura de Néel. La susceptibilidad magnética revela una patada en la temperatura de Nèel que es independiente del campo magnético externo. La susceptibilidad magnética de los procesos de enfriamiento de campo cero y enfriamiento de campo coinciden por encima de la temperatura de Néel y se bifurcan por debajo de la temperatura de Néel. La división de la susceptibilidad magnética es mayor en un campo magnético externo más bajo. No se observa más división de susceptibilidad magnética cuando la energía de anisotropía del momento magnético es menor que la energía del momento magnético a 0,7 T. Nuestro estudio apoya que estas características de susceptibilidad magnética se originan en un orden antiferromagnético acompañado de ferromagnetismo débil. La susceptibilidad magnética saturada extraída va bien con la tendencia de la cúspide de susceptibilidad magnética medida. Esto indica que la cúspide de susceptibilidad ampliamente observada podría tener su origen en el ferromagnetismo débil. La oscilación dHvA es consistente con la predicción teórica. Esto apoya que la oscilación de dHvA observada proviene del estado de la superficie topológica.
Disponibilidad de datos y materiales
Los conjuntos de datos generados durante y / o analizados durante el estudio actual están disponibles de los autores correspondientes a solicitud razonable.
Abreviaturas
- XPD:
-
Difracción de rayos X
- EDS:
-
Espectroscopia de rayos X de dispersión de energía
- ARPES:
-
Espectroscopia de fotoemisión resuelta en ángulo
- dHvA:
-
De Haas-Van Alphen
Nanomateriales
- Impresión del fusible 1 con el fusible 1
- ¡¿Qué hago con los datos ?!
- En sintonía con el corazón de un átomo de cobre
- Descubriendo el pasado con la impresión 3D
- Las propiedades eléctricas de los compuestos híbridos basados en nanotubos de carbono de paredes múltiples con nanoplaquetas de grafito
- El efecto del plasma de no equilibrio por contacto sobre las propiedades estructurales y magnéticas de Mn Х Fe3 - X О4 Espinelas
- Biosensor ultrasensible para la detección de ADN de Vibrio cholerae con nanoesferas compuestas de poliestireno-co-ácido acrílico
- Propiedades eléctricas de materiales compuestos con alineación asistida por campo eléctrico de rellenos de nanocarbono
- Los efectos de acoplamiento de los polaritones de plasma superficial y las resonancias magnéticas dipolo en metamateriales
- Síntesis controlada de BaYF5:Er3 +, Yb3 + con morfología diferente para la mejora de la luminiscencia de conversión ascendente
- Cómo dominar la gestión de pedidos al por mayor con el software adecuado



