Efectos de la anisotropía y el límite de grano en el plano en películas multicapa de Cu / Pd con interfaz cubo sobre cubo y hermanada

Resumen

En materiales cristalinos, el límite de grano y la anisotropía de la estructura cristalina afectan sus propiedades mecánicas. Los efectos de la estructura interfacial sobre las propiedades mecánicas pueden ser diversos cuando la película multicapa se carga en diferentes direcciones. En este trabajo, realizamos una serie de simulaciones de dinámica molecular de la tensión de películas multicapa de Cu / Pd monocristalinas y policristalinas en plano con interfaces de cubo sobre cubo (COC) e interfaces macladas para explorar los efectos de la estructura interfacial, dirección de carga y límites de grano en el plano en sus propiedades mecánicas. Las líneas de dislocación interfacial desajustadas se doblan después de la relajación, y se encontró que la temperatura alta de 300 K era una condición necesaria. Cuando se estira a lo largo de la dirección 〈110〉, el efecto de fortalecimiento de la interfaz COC es más notable; sin embargo, cuando se estira a lo largo de la dirección 〈112〉, el efecto de fortalecimiento de la interfaz gemela es más visible, mostrando el efecto anisotrópico de la estructura interfacial sobre las propiedades mecánicas. Sin embargo, en la muestra policristalina en forma de panal de abeja en el plano, la interfaz gemela mostró un efecto de fortalecimiento pronunciado y no se observaron dislocaciones con sacudidas.

Introducción

Las películas nanoestructuradas metálicas multicapa (NMM) han atraído mucha atención debido a sus excelentes propiedades mecánicas [1, 2, 3], que suelen ser superiores a sus constituyentes. La interfaz, zona de transición entre diferentes capas individuales, es uno de los defectos planos más comunes en las películas NMM, que pueden actuar como fuentes y sumideros de defectos mediante absorción y aniquilación, barreras y sitios de almacenamiento de defectos [4,5,6,7 ].

Las interfaces en una película NMM se pueden dividir en una interfaz coherente, semi-coherente y no coherente basada en el desajuste de la red entre sus constituyentes en ambos lados de la interfaz [4]. Las películas multicapa de cobre-paladio (Cu / Pd) y oro-níquel (Au / Ni) son las primeras películas multicapa encontradas que poseen excelentes propiedades mecánicas [8]. Yang y col. midieron el módulo de elasticidad biaxial Y [111] de películas multicapa de Cu / Pd y Au / Ni mediante pruebas de abombamiento y encontraron que su módulo de elasticidad biaxial aumentaba drásticamente de 0,27 a 1,31 TPa y de 0,21 a 0,46 TPa, respectivamente [8]. Posteriormente, Davis et al . utilizaron técnicas más avanzadas para medir las propiedades elásticas y estructurales de películas multicapa de Cu / Pd y Cu / Ni con las mismas texturas de crecimiento y amplitudes de modulación de composición [9, 10]. Sin embargo, no se ha observado un comportamiento elástico anómalo significativo [9, 10], lo que plantea si el efecto supermódulo existe en las multicapas de Cu / Pd. Las propiedades mecánicas de NMM dependen en gran medida de la estructura interfacial entre capas individuales adyacentes [11]. Howe y col. investigó la estructura interfacial de las películas de Pd en Cu (111) y encontró que el Pd crece en una estructura de FCC hermanada a lo largo de la dirección 〈111〉 [12]. Las estructuras de hermanamiento en la interfaz suelen tener un efecto profundo en su fuerza [11].

Weng y otros . investigó el efecto de la estructura interfacial sobre los comportamientos de deformación de películas multicapa de Cu / Ni con interfaces gemelas coherentes, semi-coherentes y coherentes utilizando simulación de dinámica molecular (MD) y encontró que la interfaz gemela coherente muestra un fortalecimiento significativo [7]. Sin embargo, en nuestro trabajo reciente, el efecto de fortalecimiento no aparente de la interfaz gemela en películas multicapa de Cu / Pd se observó bajo tensión a lo largo de la dirección 〈110〉 [13]. Además, la forma de la red de dislocación inadaptada cambiaría durante la minimización de energía y la relajación. Shao y col. investigó los mecanismos de relajación de las interfaces y la evolución de las redes de dislocación interfacial en las películas multicapa de Cu / Ni mediante simulaciones de MD [14, 15, 16, 17]. La dirección de carga de estas obras suele ser perpendicular a la interfaz, lo que se denomina fuera del plano [7, 18, 19]. Sin embargo, la interfaz puede desempeñar diferentes funciones durante la carga en diferentes direcciones debido a la anisotropía de las propiedades mecánicas de los cristales [20, 21, 22, 23].

Además, las películas multicapa son más propensas a someterse a la carga paralela a la interfaz en la práctica, lo que se conoce como carga en el plano. Zhou y col. propusieron un mecanismo de fortalecimiento gobernado por múltiples dislocaciones extendidas en forma de collar en un metal nano-gemelado de grano columnar sometido a tensión externa paralela a los planos gemelos [20], que también se observa en la multicapa de Cu / Ni [21]. Estas dislocaciones movidas raramente se encuentran en una simulación bajo una carga fuera del plano [7, 18, 19, 24]. En las simulaciones MD disponibles de tensiones en el plano, la muestra generalmente se estira a lo largo de una dirección específica, es decir, dirección 〈112〉 o 〈110〉 [25]. Sin embargo, se han realizado pocos estudios comparativos bajo tensión en estas dos direcciones. Por otro lado, la capa individual de la película multicapa preparada mediante experimentos suele ser policristalina en el plano que contiene muchos límites de grano (GB) perpendiculares a la interfaz.

Las dislocaciones escalonadas mencionadas anteriormente se observan a menudo en las películas trenzadas coherentes o películas trenzadas de múltiples capas con un pequeño desajuste. Aún se desconoce si estas dislocaciones de jog pueden formarse en una película de interfaz gemela con un alto desajuste. La película multicapa de Cu / Pd es la película multicapa más antigua que se ha encontrado con excelentes propiedades mecánicas [8, 12, 26,27,28]. Su desajuste de celosía (~ 7,07%) es mayor que el de las películas multicapa de Cu / Ni (~ 2,7%). Por lo tanto, el mecanismo de fortalecimiento y debilitamiento [7, 14,15,16,17] obtenido por la película multicapa de Cu / Ni puede no aplicarse a la película multicapa de Cu / Pd. Se observan dos interfaces comunes [3], la interfaz gemela y la interfaz cubo sobre cubo, en películas multicapa de Cu / Pd mediante caracterización experimental [12]. Comprender el efecto de la estructura interfacial en las propiedades mecánicas de las películas multicapa sería importante para diseñar películas nano multicapa de alto rendimiento con un gran desajuste de celosía.

En este trabajo se desarrollan dos tipos de muestras con cristal alveolar en plano y monocristal. Para cada tipo de muestra, se consideran dos tipos de interfaces (cubo sobre cubo y gemela). Luego, realizamos una serie de simulaciones de tensión MD de estas películas multicapa de Cu / Pd para explorar los efectos de la estructura interfacial, la dirección de carga y los GB en el plano sobre sus propiedades mecánicas.

Métodos

Es necesario identificar tres conjuntos de parámetros para Cu – Cu, Pd – Pd y Cu – Pd, respectivamente. Elegimos el potencial del segundo método del átomo incrustado modificado del vecino más cercano (2NN MEAM) [29, 30] para describir las interacciones entre los átomos. Para Cu-Cu y Pd-Pd, sus parámetros potenciales han sido desarrollados por Lee et al. [31]. Basándonos en los parámetros de potencial de los elementos individuales, ajustamos un conjunto de parámetros de potencial binario de Cu – Pd en nuestro trabajo anterior [26], como se indica en la Tabla 1. Estos parámetros pueden reproducir las propiedades físicas y mecánicas fundamentales de Cu, Pd y sus aleaciones y describen el mecanismo de formación de gemelos de crecimiento [26].

La película de varias capas FCC / FCC tiende a crecer a lo largo de las direcciones 〈111〉 y la relación de orientación de la interfaz se identifica como {111} _FCC / {111} _FCC [32, 33]. Por lo tanto, solo consideramos las interfaces Cu {111} / Pd {111} en este trabajo. Se construyen dos tipos de muestras con monocristal en plano (SC) y cristal de panal (HC), como se muestra en la Fig. 1a y b. Para cada tipo de muestra, se consideran cubo sobre cubo (COC) y la interfaz gemela. Por lo tanto, se construyen cuatro muestras, denominadas SC COC, SC Twin, HC COC y HC Twin. Para SC COC, las orientaciones de los cristales de la capa de Cu y la capa de Pd son idénticas; sin embargo, para SC Twin, las orientaciones de sus cristales son simétricas con respecto a la interfaz del gemelo, como se muestra en el recuadro de la Fig. 1a. Las relaciones de orientación y las dimensiones de cada dirección se enumeran en la Tabla 2.

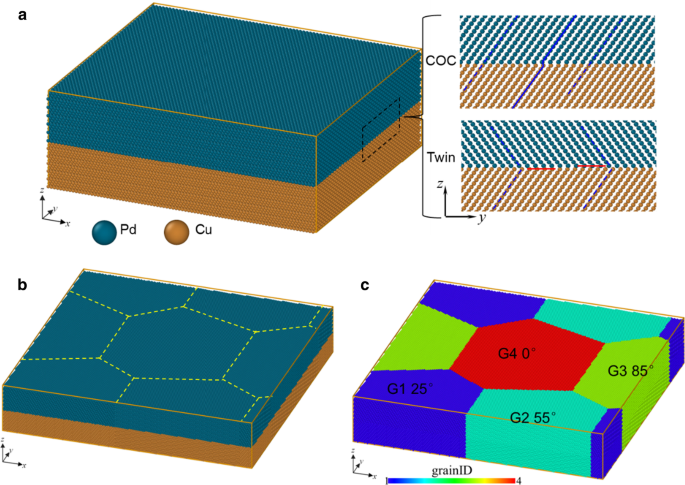
El modelo atómico con a en el plano monocristal y b cristal de panal. c Las relaciones de orientación de cada grano con respecto al monocristal. Los recuadros de la Fig. 1a son la distribución atómica de COC y las interfaces gemelas, donde las líneas rojas representan gemelos

La muestra de panal en el plano se construye utilizando el método de construcción de Voronoi con el monocristal en el plano como una unidad representativa, como se muestra en la Fig. 1b. En las muestras de HC, hay cuatro granos, cuyas relaciones de orientación con respecto al monocristal (Fig. 1a) son una rotación en sentido antihorario de 25 °, 55 °, 85 ° y 0 ° alrededor de la z -eje, respectivamente. Los tamaños de HC COC y HC Twin se enumeran en la Tabla 2.

La minimización de energía se utiliza en primer lugar para optimizar la estructura interfacial a 0 K. Luego, la relajación se realiza en cada muestra bajo el conjunto isotérmico-isobárico (NPT) [34, 35] a 300 K durante 20 ps para lograr un sistema de equilibrio con presión cero en x -, años - y z - direcciones. Simulaciones de tensión uniaxial de SC COC y SC Twin en diferentes direcciones ( x - o años -) con una tasa de deformación de 5 × 10 ⁸ s ⁻¹ se realizan con el Simulador masivamente paralelo atómico / molecular a gran escala (LAMMPS) [36]. También realizamos simulaciones de tracción de HC COC y HC Twin para estudiar los efectos de los GB en el plano y las estructuras interfaciales en sus propiedades mecánicas. Durante la carga, las presiones en las otras dos direcciones se mantienen a cero para satisfacer el requisito de deformación por tracción uniaxial. En todas las simulaciones, las condiciones de contorno periódicas se aplican a lo largo del x- , y- y z -direcciones.

Elegimos el algoritmo de extracción de dislocaciones (DXA) [37] para analizar las estructuras locales, mediante el cual los átomos se pueden dividir en diferentes tipos (FCC, BCC, HCP, etc.) en función de sus estructuras locales. Puede identificar las dislocaciones comunes en el cristal de FCC y determinar sus vectores de Burgers y líneas de dislocación de salida [37]. Los átomos se colorean según la siguiente regla:verde para FCC, rojo para HCP, azul para BCC y blanco para "otras" estructuras cristalinas locales. Se sabe que tanto las fallas de apilamiento (SF) como los límites / interfaces gemelos (TB / TI) se identifican como estructuras HCP, y dos capas atómicas rojas adyacentes y la capa atómica roja única son SF y TB / TI, respectivamente. Se utiliza un software de visualización de código abierto, OVITO [38], para visualizar la evolución de las microestructuras.

Resultados y discusión

Caracterización de estructuras interfaciales

La Figura 2 muestra la configuración atómica interfacial en SC COC y SC Twin después de la minimización y relajación de energía, donde los átomos identificados como FCC se han eliminado para mayor claridad. En la Fig. 2, podemos ver que la red de dislocación de desajuste de interfaz tiene una periodicidad triangular, lo que es consistente con la de la película multicapa de Ag (111) / Ni (111) [39]. La diferencia es que la interfaz en SC COC se compone de regiones coherentes alternas (CR) y regiones SF. Por el contrario, la interfaz de SC Twin está compuesta en su totalidad por TB. Estos TB están en capas atómicas adyacentes y están compuestos por átomos de Cu y Pd alternados en triángulos adyacentes, lo que también puede confirmarse por la altura de las dos líneas sólidas rojas (representan los TB) en el recuadro de la Fig. 1a. Durante la minimización de energía, la energía potencial del sistema se minimiza por el ligero movimiento de los átomos y el tamaño de las muestras en cada dirección no puede cambiar libremente. En esta etapa, se trata principalmente de optimizar la estructura local, específicamente, la estructura interfacial. Por lo tanto, las líneas de dislocación permanecen rectas después de la minimización de energía, como se muestra en la Fig. 2a y b. Durante la minimización de energía, el tamaño de la muestra es fijo, lo que induciría tensiones residuales en todas las direcciones. Estas tensiones residuales no se pueden eliminar lo suficiente después de la minimización de energía.

Configuración atómica interfacial después de la minimización de energía: a SC COC, b SC Twin, y después de la relajación: c SC COC, d SC Twin. Las bolas atómicas grandes y pequeñas representan Pd y Cu, respectivamente. Los átomos identificados como FCC se han eliminado para mayor claridad

Durante la relajación, el tamaño de la muestra permite cambiar para relajar la tensión residual a presión cero en todas las direcciones. Después de la relajación, las líneas de dislocación inadaptadas se doblan (fig. 2c, d). Este fenómeno de la red de dislocación inadaptada también se puede encontrar en la interfaz semi-coherente Cu {111} / Ni {111} [40, 41]. Al comparar el número de átomos con diferentes estructuras locales, especialmente HCP, podemos encontrar que el número de átomos en diferentes estructuras reticulares cambia de manera insignificante, lo que indica que el área total de SF y TB varía de manera insignificante.

Para explorar si la temperatura es una condición necesaria para la flexión de las líneas de dislocación, las muestras después de la minimización se relajan a una temperatura baja de 10 K para comparar y encontrar que las líneas de dislocación permanecen rectas. Por lo tanto, una temperatura más alta es una condición necesaria para provocar la flexión de la línea de dislocación. Específicamente, debido al aumento de la activación térmica a altas temperaturas, los átomos alrededor de las líneas de dislocación pueden volcar la barrera de energía para moverse de una columna atómica a la columna atómica adyacente densamente empaquetada. Por lo tanto, la magnitud de flexión de la dislocación es solo de una a dos distancias de capa atómica. También se puede observar una flexión similar de la línea de dislocación en la red de dislocación en las muestras con cristales de panal en el plano (HC COC y HC Twin).

Efectos de la dirección de carga

La Figura 3 muestra la tensión-deformación ( σ - ε ) curvas de SC COC y SC Twin bajo tensión en diferentes direcciones a una tasa de deformación de 5 × 10 ⁸ s ⁻¹ , donde se puede ver que todas estas curvas crecen linealmente hasta el punto más alto, luego caen rápidamente a un cierto valor y fluctúan alrededor de ellas. El módulo de los jóvenes E se obtiene ajustando la pendiente de las curvas en un rango de deformación de 0,00-0,03, como se indica en la Tabla 3 . Podemos ver que E a lo largo de y \ ([\ overline {2} 11] \) (145,62 GPa para SC COC y 142,95 para SC Twin) es más grande que los de x \ ([01 \ overline {1}] \) (135,04 GPa para COC y 133,84 GPa para Twin). El E s en la misma dirección pero con diferentes estructuras interfaciales son casi idénticas, mostrando una dependencia insignificante de E s sobre estructuras interfaciales involucradas en este trabajo, que es consistente con los resultados experimentales de películas multicapa de Cu-Co [42], Cu / Pd y Cu / Ni [9].

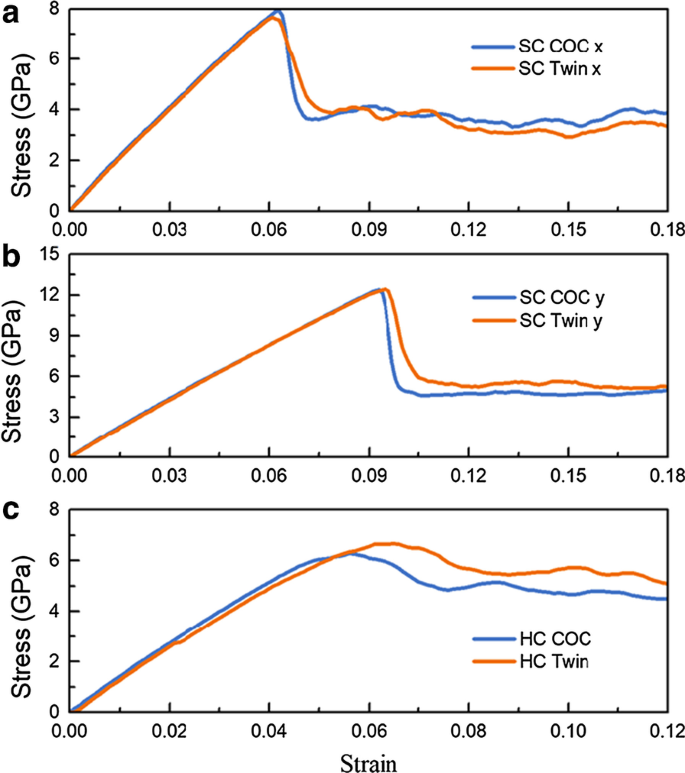
El σ - ε curvas de muestras bajo tensión a una tasa de deformación de 5 × 10 ⁸ s ⁻¹ . SC COC y SC Twin junto a a x \ ([01 \ overline {1}] \) y b y \ ([\ overline {2} 11] \) dirección. c HC COC y HC Twin a lo largo de x- eje

En un material cúbico, los módulos elásticos a lo largo de cualquier orientación se pueden determinar a partir de las constantes elásticas mediante la aplicación de la siguiente ecuación [22]:

$$ \ frac {1} {{E_ {ijk}}} =S_ {11} - 2 \ left ({S_ {11} - S_ {12} - \ frac {1} {2} S_ {44}} \ derecha) \ veces \ izquierda ({l_ {i1} ^ {2} l_ {j2} ^ {2} + l_ {j2} ^ {2} l_ {k3} ^ {2} + l_ {i1} ^ {2} l_ {k3} ^ {2}} \ derecha), $$ (1)

donde S ₁₁ , S _12, y S ₄₄ son constantes de cumplimiento elástico; E _ijk es el módulo de Young en el [ ijk ] dirección; l _i1 , l _j2 y l _k3 son los cosenos de la dirección [ ijk ]. Sin embargo, los coeficientes sobre la dirección del cristal \ (\ left ({l_ {i1} ^ {2} l_ {j2} ^ {2} + l_ {j2} ^ {2} l_ {k3} ^ {2} + l_ { i1} ^ {2} l_ {k3} ^ {2}} \ right) \) en la ecuación. (1) a lo largo de 〈112〉 y 〈110〉 las direcciones son idénticas (0.25), por lo tanto, para Cu y Pd, E _〈112〉 = E _〈110〉 . Cuando la deformación es paralela a la interfaz, la regla de mezcla, \ (E _ {[ijk]} ^ {{\ text {Cu / Pd}}} =E _ {[ijk]} ^ {{{\ text {Cu}} }} f _ {{{\ text {Cu}}}} + E _ {[ijk]} ^ {{{\ text {Pd}}}} f _ {{{\ text {Pd}}}} \), puede ser utilizado para calcular E . f _Cu y f _Pd son la fracción de volumen de Cu y Pd, respectivamente, y f _Cu + f _Pd =1. En este trabajo, f _Cu y f _Pd son invariantes para muestras con diferentes interfaces. Por lo tanto, \ (E _ {{\ left \ langle {112} \ right \ rangle}} ^ {{\ text {Cu / Pd}}} \) debe ser igual a \ (E _ {{\ left \ langle {110} \ right \ rangle}} ^ {{\ text {Cu / Pd}}} \). Sin embargo, el E s a lo largo de 〈110〉 y 〈112〉 son diferentes, lo que debe atribuirse a la anisotropía elástica de la zona afectada por la interfaz [6, 42].

La tensión máxima ( σ _m ) obtenido por tensión a lo largo de y -axis es más grande que a lo largo de x -eje para COC y la interfaz gemela, que debe atribuirse al factor de Schmidt μ . El σ _m de la curva corresponde a la nucleación de la dislocación [43, 44, 45]. μ =Cos φ cos λ , donde φ y λ son el ángulo entre la dirección de tracción y la dirección normal del plano de deslizamiento y el ángulo entre la dirección de tracción y la dirección de deslizamiento, respectivamente. Además, cuando la tensión está a lo largo de x \ ([01 \ overline {1}] \), el σ _m y la cepa correspondiente ε _m de SC COC es ligeramente más alta que la de SC Twin, lo que es consistente con el trabajo de Weng et al. [25]. Sin embargo, cuando la tensión está a lo largo de y \ ([\ overline {2} 11] \), el σ _m y ε _m de SC COC son ligeramente más bajas que las de SC Twin. Además, realizamos simulaciones MD adicionales a una tasa de deformación más baja de 1 × 10 ⁸ s ⁻¹ y obtuvo resultados similares. Sin embargo, en general, la diferencia entre ellos es leve y casi se puede ignorar.

Una vez que la tensión alcanza el punto más alto, muchas dislocaciones se nuclean sucesivamente para liberar la energía potencial elástica almacenada, lo que provoca la rápida caída de la tensión [46]. La interacción entre las dislocaciones, la interacción entre las dislocaciones y la interfaz, y la nucleación de nuevas dislocaciones son el mecanismo principal en la etapa de flujo-estrés. El σ _f es el esfuerzo promedio en 0.121 < ε <0.150, como se indica en la Tabla 3. A diferencia de la pequeña diferencia en E , σ _m y ε _m , la diferencia entre σ _f para las diferentes estructuras interfaciales es significativo. Cuando la tensión está a lo largo de x \ ([01 \ overline {1}] \), el σ _f de SC COC es más grande que el de SC Twin, lo que demuestra que el efecto de fortalecimiento de la interfaz COC es más obvio que el de la interfaz Twin, lo cual es consistente con el trabajo de Weng et al. [25]. Sin embargo, cuando la tensión está a lo largo de y \ ([\ overline {2} 11] \), el σ _f de SC Twin es un 15,55% más grande que el de SC COC, mostrando un evidente fortalecimiento de la interfaz gemela, que concuerda con la cognición tradicional del efecto de fortalecimiento del límite gemelo. La comparación de la tensión de flujo en estas dos direcciones muestra que el efecto de fortalecimiento de la estructura interfacial depende de la dirección de carga. En la sección de flujo, examinaremos la respuesta mecánica de muestras de cristales en forma de panal en el plano.

Efectos de GB en el plano

Además, realizamos una simulación de tensión MD de HC COC y HC Twin a una tasa de deformación de 5 × 10 ⁸ s ⁻¹ y el σ - ε La curva se muestra en la Fig. 3c. Del mismo modo, podemos obtener E , σ _m , ε _m y σ _f , como se indica en la Tabla 3. Tenga en cuenta que E se obtiene ajustando la pendiente de σ - ε curvas de HC COC y HC Twin en un rango de deformación de 0.0–0.02, y σ _f es el esfuerzo promedio en 0.081 < ε <0,100. Para HC COC y HC Twin, el E s están cerca y se encuentran entre el de la muestra SC largo el x \ ([01 \ overline {1}] \) y y \ ([\ overline {2} 11] \). El E s son ligeramente más grandes que los experimentales (115-125 GPa) [9], que deberían atribuirse a las muestras atómicas idealizadas utilizadas en este trabajo sin tener en cuenta los defectos adicionales como las vacantes y las impurezas. Su σ _m es menor que el de la muestra SC, lo que puede atribuirse a que las dislocaciones son más fáciles de nuclear inducidas por la concentración de estrés local con la introducción de GB en el plano. Tomando la interfaz gemela como ejemplo, la Fig.4 muestra la microestructura de la ubicación de nucleación de la dislocación después de que la tensión alcanza el punto más alto, donde se puede ver que en HC Twin, la dislocación se nuclea desde la unión del GB y la interfaz gemela (Fig. . 4a), mientras que en las muestras de SC Twin, la dislocación se nuclea desde la interfaz de los gemelos, ambos estirados a lo largo de x \ ([01 \ overline {1}] \) (Fig. 4b) y y \ ([\ overline {2} 11] \) (Fig. 4c).

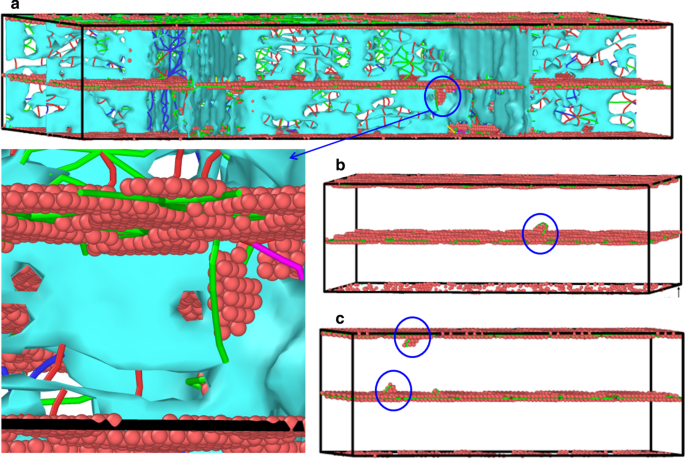
La microestructura de la ubicación de nucleación de la dislocación después de que la tensión alcanza el punto más alto. un HC Twin, SC Twin bajo tensión a lo largo de b x \ ([01 \ overline {1}] \), c y \ ([\ overline {2} 11] \)

Aunque el σ _m de la muestra de HC es menor que los de la muestra de SC, el σ _f de la muestra de HC es mayor que la muestra de SC, lo que indica el efecto de fortalecimiento de los GB en el plano. Este fortalecimiento proviene principalmente de los siguientes aspectos:(1) Los GB en el plano proporcionan más puntos de nucleación para las dislocaciones que resultan en más dislocaciones nucleadas, y estas dislocaciones se ven obstaculizadas por el COC y la interfaz gemela; (2) Los GB en el plano dificultan las dislocaciones. Además, σ _f de HC Twin es más alto que los de HC COC, lo que muestra que los efectos de fortalecimiento de la dislocación obstaculizada por la interfaz gemela son más evidentes que los de la interfaz COC.

La Figura 5 muestra la microestructura de HC Twin en la etapa de flujo de plástico. Cabe señalar que durante la carga, la nucleación y el deslizamiento de las dislocaciones parciales que forman FS, el movimiento de estas dislocaciones y las FS limitadas por la interfase que induce un deslizamiento parcial de la dislocación en forma de horquilla y las reacciones mutuas de las dislocaciones parciales que forman la dislocación de la barra de escalera son el mecanismo de deformación primario. No se observan dislocaciones múltiples en forma de collar, que a menudo se observan en películas multicapa de Cu / Ni [21] y Cu nano-maclados [20] bajo tensión en el plano. Se debe principalmente al gran desajuste de celosía de la película multicapa de Cu / Pd con una estructura de interfaz más complicada (Fig. 2).

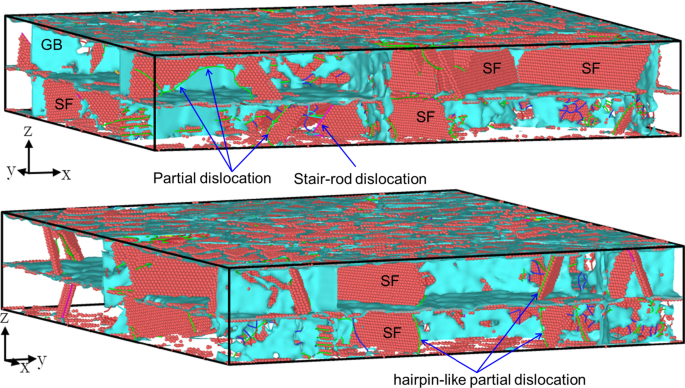
La microestructura de HC Twin en la etapa de flujo de plástico

En comparación con los materiales monocristalinos, las propiedades mecánicas de las muestras policristalinas suelen depender más de la velocidad de deformación. Por lo tanto, realizamos más simulaciones MD de tensión para muestras de HC (HC COC y HC Twin) a lo largo de x -direction y SC Twin a lo largo de x- y y -direcciones que utilizan una velocidad de deformación variada de 5 × 10 ⁷ s ⁻¹ hasta 5 × 10 ⁹ s ⁻¹ . El σ - ε Las curvas se muestran en la Fig. 6a yb, donde se puede ver que la tensión aumenta linealmente hasta el punto más alto y luego disminuye. Para las muestras de HC, la tensión fluctúa con el aumento de la tensión a una tasa de tensión baja en la etapa descendente, mientras que la fluctuación de la tensión no es aparente a una tasa de tensión alta (Fig. 6a yb). La Figura 6c yd muestra las variaciones de σ _m y σ _f contra la tasa de deformación, donde σ _m y σ _f aumenta con el aumento de la tasa de deformación. El σ _m de SC Twin a lo largo de y -La dirección es mucho mayor que la de otras muestras, lo que debería atribuirse al factor de Schmidt μ mencionado anteriormente. Sin embargo, debido al efecto de fortalecimiento del límite de grano en el plano, el σ _f de las muestras de HC están cerradas a las de SC Twin a lo largo de y dirección. Además, σ _f de las muestras con la interfaz hermanada son más altas que las que tienen la interfaz COC a una tasa de deformación alta (1 × 10 ⁸ s ⁻¹ hasta 5 × 10 ⁹ s ⁻¹ ), lo que indica el efecto de fortalecimiento de la interfaz hermanada, pero a medida que aumenta la velocidad de deformación, este efecto de fortalecimiento se debilita. Cabe señalar que a la tasa de deformación de 5 × 10 ⁷ s ⁻¹ , el σ _f de HC Twin es menor que la de HC COC, lo que puede atribuirse al hecho de que el número de dislocaciones nucleadas a una tasa de deformación baja induce menos el efecto de debilitamiento y fortalecimiento de la interfaz gemela.

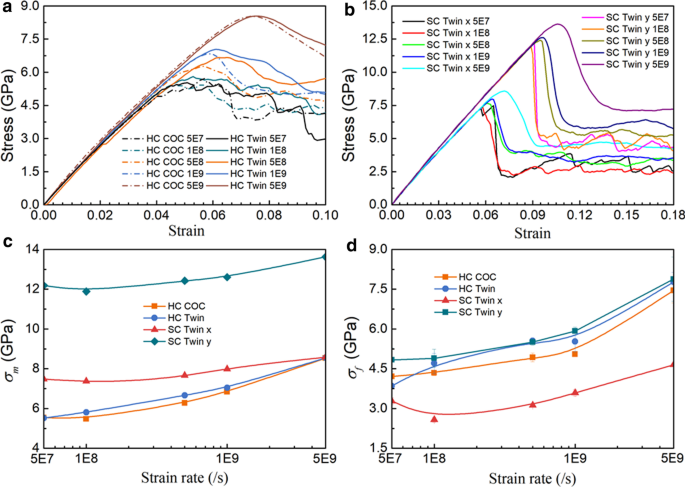
un σ - ε curvas de muestras de HC bajo tensión a lo largo de x- dirección a diferentes velocidades de deformación, b σ - ε curvas de SC Twin bajo tensión a lo largo de x- y y- dirección a diferentes velocidades de deformación. c-d Variaciones de σ _m y σ _f contra la tasa de deformación

Conclusiones

En este trabajo, se realizaron simulaciones de tensión de dinámica molecular de películas multicapa de Cu / Pd policristalinas y simples en el plano con COC e interfaces macladas a lo largo de varias direcciones para explorar los efectos de la estructura interfacial, la dirección de carga y los límites de grano en el plano en la mecánica. propiedades. Descubrimos que las dislocaciones interfaciales inadaptadas presentan una estructura de red triangular, y las líneas de dislocaciones inadaptadas se doblan después de la relajación. La alta temperatura de 300 K fue una condición necesaria para la flexión de la línea de dislocación. El módulo elástico de la muestra no tiene una dependencia obvia de la estructura de la interfaz, pero está relacionado con la dirección de carga. El efecto de fortalecimiento de la interfaz COC se nota cuando se estira a lo largo de la dirección 〈110〉; sin embargo, el efecto de fortalecimiento de la interfaz gemela es visible, cuando se estira a lo largo de la dirección 〈112〉, mostrando el efecto anisotrópico de la estructura interfacial sobre las propiedades mecánicas. Finalmente, en el modelo policristalino de panal de abeja en el plano, la interfaz gemela mostró un efecto de fortalecimiento pronunciado y no se observaron dislocaciones con sacudidas.

Disponibilidad de datos y materiales

Los conjuntos de datos utilizados o analizados durante el estudio actual están disponibles a través de los autores correspondientes previa solicitud razonable.

Abreviaturas

Cu:: Cobre
Pd:: Paladio
Ni:: Níquel
Ag:: Plata
COC:: Cubo sobre cubo
NMM:: Nanoestructurado metálico multicapa
GB:: Límite de grano
MD:: Dinámica molecular
2NN MEAM:: Método de átomo incrustado modificado del segundo vecino más cercano
FCC:: Cúbico centrado en la cara
CCO:: Cúbico centrado en el cuerpo
HCP:: Hexagonal compacto
SC:: Monocristal
HC:: Cristal de panal
LAMMPS:: Simulador masivo paralelo atómico / molecular a gran escala
NPT:: Número constante de partículas, presión y temperatura
DXA:: Algoritmo de extracción de dislocaciones
SF:: Fallo de apilamiento
TB:: Límite gemelo
TI:: Interfaz gemela
σ - ε :: Estrés-tensión
E :: Módulo de Young
σ _m :: Estrés máximo

Detección altamente sensible y selectiva de gas H2S usando películas gruesas de CuO / SnO2 hechas por precipitación e impregnación Biosensor longitudinal de capacitancia depositada con nanocompuestos de óxido de hierro y zeolita para interleucina-3 en la detección de sepsis

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias