Dos efectos de transparencia inducidos por plasma conmutables en un sistema con resonadores de grafeno distintos
Resumen
Los sistemas plasmónicos generales para realizar el efecto de transparencia inducida plasmónicamente (PIT) solo existen un solo PIT principalmente porque solo permiten una única vía de acoplamiento. En este estudio, proponemos un sistema distinto basado en resonadores de grafeno, que se compone de nanocintas de grafeno (GNR) junto con resonadores de capa de grafeno cargados con rejillas dieléctricas, para lograr dos efectos PIT conmutables. Al diseñar direcciones cruzadas de los resonadores, el sistema propuesto existen dos efectos PIT diferentes caracterizados por diferentes posiciones resonantes y anchos de línea. Estos dos efectos PIT son el resultado de dos vías de acoplamiento separadas y selectivas de polarización, lo que nos permite cambiar el PIT de uno a otro simplemente cambiando la dirección de polarización. Se realizan estudios paramétricos para demostrar los efectos de acoplamiento mientras que se aplica el modelo de dos partículas para explicar el mecanismo físico, encontrando excelentes concordancias entre los resultados numéricos y teóricos. Nuestra propuesta se puede utilizar para diseñar dispositivos plasmónicos conmutables basados en PIT, como sensores sintonizables de doble banda y absorbedores perfectos.
Introducción
Los plasmones de superficie son los modos colectivos de resonancia de electrones libres que se generan en la interfaz entre los medios aislantes y conductores [1, 2]. Debido a su capacidad para confinar un campo electromagnético incidente al tamaño límite último de la escala de un átomo en el rango de sublongitud de onda [3], los plasmones de superficie se han convertido en uno de los métodos más fundamentales e importantes para lograr fuertes interacciones luz-materia [4] . Este atractivo fenómeno óptico se ha encontrado en varios tipos de sistemas plasmónicos, lo que facilita el desarrollo de una variedad de aplicaciones de vanguardia como biosensores [5], óptica no lineal [6, 7], absorbentes [8,9 , 10,11] y otros moduladores plasmónicos [12,13,14,15]. Las posibilidades de lograr estas importantes aplicaciones se atribuyen a algunos fenómenos interesantes como la transparencia inducida plasmónicamente (PIT). El proceso conocido como PIT es una consecuencia de la interferencia Fano acoplada al campo cercano y se caracteriza por la generación de una ventana prominente en un espectro óptico, ya que elimina la absorción resonante en el sistema. Durante los últimos años, dicha interacción plasmónica coherente se ha utilizado para lograr una variedad de aplicaciones, como la conmutación plasmónica [16], la propagación lenta de la luz [17] y la detección [18] y el almacenamiento óptico [19].
Aunque estudios recientes han revelado que las películas de metal ultradelgadas hasta el espesor atómico pueden poseer sintonía eléctrica dinámica [20, 21], los plasmones soportados por estos nuevos metales todavía sufren pérdidas óhmicas y radiativas relativamente grandes de los metales [22, 23]. Tal deficiencia de los metales limita el desarrollo posterior de PIT soportado por metal, y es necesario encontrar nuevos materiales plasmónicos. A diferencia de los plasmones metálicos, los plasmones soportados por grafeno (una única capa atómica de átomos de carbono fuertemente estructurados formada en una red hexagonal simétrica en forma de panal) no solo se pueden ajustar de forma continua y dinámica a través de polarización electrostática [24, 25], sino que también tienen una propagación prolongada de longitud, lo que permite una nueva generación de dispositivos plasmónicos reestructurables y, por lo tanto, proporciona una plataforma ideal para lograr PIT activo [26, 27]. Aunque se han utilizado varios materiales y diseños para lograr PIT en metal puro [16, 28,29,30,31] y grafeno [32,33,34,35,36,37,38,39,40,41,42] , o sus sistemas híbridos basados en materiales [43, 44, 45], la mayoría de estos sistemas solo pueden realizar un único efecto PIT. Por ejemplo, una de las formas comunes de lograr PIT es diseñar π -metasuperficies con forma / similar [16, 28, 30, 33, 37, 45]. Otra forma es construir sistemas acoplados a rejillas [32, 34]. Sin embargo, este tipo de estructuras solo pueden realizar PIT de ventana única dependiente de la polarización. Esto se debe a que, debido a la especial asimetría geométrica de estas estructuras, todos los resonadores nanoestructurados están preconfigurados para funcionar como modo brillante (radiativo / superradiante) u oscuro (no radiativo / subradiante). Por lo tanto, solo permiten una vía de acoplamiento de brillante a oscuro en una dirección de polarización particular, lo que da como resultado un solo efecto PIT dependiente de la polarización. Aunque nuestros estudios anteriores han demostrado sistemas PIT con dos vías de acoplamiento de modo brillante-oscuro en nanocintas de grafeno puro (GNR) [35] o estructuras acopladas a rejilla [38], el PIT de ventana única insensible a la polarización tally o doble dependiente de polarización Los efectos de la ventana PIT en estos sistemas dependen en gran medida de la elección particular de los parámetros geométricos (ver la parte de discusión).
En este artículo, proponemos utilizar dos resonadores distintos, a saber, los GNR acoplados con una hoja de grafeno cargada con rejillas dieléctricas, para acoplar y realizar dos efectos PIT separados. Demostraremos que al establecer direcciones de resonancia perpendiculares, los plasmones de superficie que resuenan en ambos resonadores se generarán bajo diferentes direcciones de polarización de la luz incidente, lo que dará como resultado dos vías de acoplamiento dependientes de la polarización diferentes y, por lo tanto, dos efectos PIT separados. Además, se utilizarán estudios paramétricos para investigar en detalle los mecanismos de acoplamiento. Y tanto las simulaciones avanzadas como los análisis teóricos basados en modelos de dos partículas se combinarán para demostrar estos efectos PIT intercambiables. Finalmente, se discutirán las aplicaciones potenciales del sistema propuesto, como sensores de índice de refracción y absorbedores perfectos, y las comparaciones con otros sistemas PIT.
Diseños y materiales
En esta parte, presentamos el modelo numérico y los materiales relacionados utilizados en este estudio. Afirmamos que en nuestro modelo, solo consideramos la electrodinámica clásica y descuidamos cualquier efecto que pueda surgir de los posibles efectos cuánticos de tamaño finito de los GNR, los efectos no lineales del grafeno y los efectos de fonones del sustrato [46]. El esquema del sistema propuesto se muestra en la Fig. 1. Se colocan dos capas de grafeno en la x o y plano y separados por un Si o SiO dopado 2 conductor con índice de refracción n 3 y espesor d . La primera capa está formada por nanocintas de grafeno inferiores (LGNR) con un punto en la x dirección. La segunda capa es una hoja entera de grafeno, que además está cubierta por rejillas dieléctricas con un índice de refracción n 1 (etiquetado como rejillas superiores de grafeno, UGG) y un punto P d en el y dirección. Los parámetros geométricos se fijan como W r = W d =50 nm, p r = p d =100 millas náuticas, h =100 nm y d =20 nm, como se define en la Fig. 1. Las constantes dieléctricas de los otros materiales que rodean las capas de grafeno se establecen en n 0 y n 2 , que se muestra en la Fig. 1. Por simplicidad y sin pérdida de generalidad, se supone que las constantes dieléctricas son n 1 =2.0 y n 0 = n 2 = n 3 =1.0. El descuido de la parte imaginaria del índice de refracción no cambiaría las conclusiones fundamentales de este estudio. Tenga en cuenta que los parámetros anteriores se mantienen iguales a menos que se especifique lo contrario. Tecnológicamente, la realización del sistema PIT basado en grafeno de dos capas diseñado es experimentalmente factible utilizando técnicas de patrón y rejilla bien desarrolladas, que se han utilizado recientemente para fabricar el sistema de grafeno en capas [27, 47].
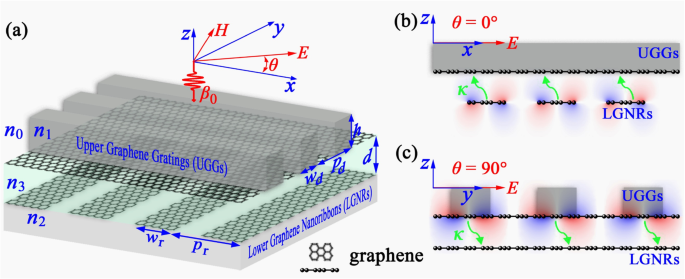
3D ( a ) y vistas laterales 2D ( b , c ) del sistema PIT propuesto. Una capa de grafeno cargada con rejilla dieléctrica periódica cubre por encima de una capa de GNR periódicos con rejilla cruzada y direcciones de cinta. La capa superior de rejilla de grafeno está diseñada con un ancho de rejilla W d , altura h y período transversal P d , mientras que las nanocintas de grafeno inferiores tienen un ancho de cinta W r y punto P r . La distancia entre las dos capas de grafeno es d , que se supone que está lleno de Si o SiO 2 conductivo espaciador con índice de refracción n 3 . Los índices de refracción de y sobre las rejillas dieléctricas y debajo de los GNR están etiquetados como n 1 , n 0 y n 2 , respectivamente. Una onda plana polarizada linealmente con un número de onda β 0 y ángulo de polarización θ con respecto a la x -El eje normalmente incide en la superficie del sistema de grafeno en capas
Métodos
La estructura propuesta se simula numéricamente utilizando el método de dominio de tiempo de diferencia finita (FDTD) basado en Lumerical FDTD Solutions. En nuestras simulaciones, las condiciones de contorno periódicas se utilizan tanto en las direcciones x como en y. Las ondas planas de banda ancha inciden en la dirección z, a lo largo de las cuales se aplican capas perfectamente adaptadas para absorber toda la luz que sale de los límites. La distribución del campo eléctrico se recopila mediante monitores de perfil de campo 2D en la longitud de onda resonante con una distancia de 0,5 nm a la superficie del grafeno entre las dos capas. Además, la película de grafeno se describe dentro de la aproximación de fase aleatoria (RPA) [48, 49]. Dentro de esta aproximación, la conductividad óptica en el plano σ de grafeno se escribe como una expresión semiclásica similar a Drude en el rango del infrarrojo medio como σ ( ω ) = es decir 2 E F / [ πћ 2 ( ω + iτ −1 )] [24, 50]. Aquí, E F = ћν F ( n g π ) 1/2 es el nivel de Fermi de grafeno, con n g = ( μ / ћν F ) 2 / π siendo la concentración de portador (donde μ =15.000 cm 2 / ( V × s ) es la movilidad de CC medida, ν F =10 6 m / s es la velocidad de Fermi y ћ es la constante reducida de Plank) y se puede ajustar mediante compuertas eléctricas [24, 25, 50], ω es la frecuencia angular, y τ =μE F / ( ev F 2 ) es el tiempo de relajación del portador. En este documento, E F se fija en 0,6 eV a menos que se especifique lo contrario. En nuestras simulaciones, la propiedad óptica del grafeno se describe mediante el uso de un tensor de permitividad relativa anisotrópico [35]. La z componente de la permitividad del grafeno se establece como ε zz =2.5 basado en la constante dieléctrica del grafito, mientras que los componentes en el plano son ε xx = ε yy =2.5 + iσ ( ω ) / ( ε 0 ωt ) [24, 51], con ε 0 es la permitividad del vacío y t =1 nm es el espesor del grafeno [35].
Al aplicar el modelo de dos partículas en ambos x y y ejes, podemos analizar teóricamente las resonancias plasmónicas efectivas y los acoplamientos que se muestran en la Fig. 1 mediante el siguiente conjunto de ecuaciones [8, 52, 53]:
$$ {a} _ {1i} ^ {{\ prime \ prime}} (t) + {\ gamma} _ {1i} {a} _ {1i} ^ {\ prime} (t) + {\ omega} _ {1i} ^ 2 {a} _ {1i} (t) + {\ kappa} _ {12i} ^ 2 {a} _ {2i} (t) ={Q} _ {1i} E \ sin \ theta / {m} _ {1i} $$ (1) $$ {a} _ {2i} ^ {{\ prime \ prime}} (t) + {\ gamma} _ {2i} {a} _ {2i} ^ {\ prime} (t) + {\ omega} _ {2i} ^ 2 {a} _ {2i} (t) + {\ kappa} _ {21i} ^ 2 {a} _ {1i} (t) ={Q} _ {2i} E \ cos \ theta / {m} _ {2i} $$ (2)donde i = x o años ; γ i es el factor de pérdida, que se relaciona con el ancho de línea del espectro; ω i es la frecuencia de resonancia del resonador; Q i son las cargas efectivas de los modos, que muestran la fuerza del modo resonante; y m i son las masas efectivas de las partículas en la correspondiente orientación resonante. κ i es la fuerza de acoplamiento entre las dos capas en el i dirección, que corresponde a las interacciones electrón-electrón de los dos modos acoplados y, por lo tanto, está determinada por la distribución especial del campo de los plasmones y la distancia de acoplamiento entre los resonadores. Considerando que los acoplamientos plasmónicos son solo a lo largo de los dos ejes de coordenadas con fuerza de acoplamiento κ 12 i = κ 21 i = κ i , podemos tratar el sistema como dos grupos separados de resonadores que resuenan independientemente en diferentes direcciones. Suponemos que todas las partículas se acoplan con el campo eléctrico incidente E = E 0 e iωt , generando los vectores de desplazamiento a i = c i e iωt . Después de realizar algunos cálculos algebraicos en las Ecs. (1) y (2), las amplitudes modales de los plasmones se pueden expresar como:
$$ {a} _ {1i} (t) =\ frac {\ kappa_i ^ 2 {Q} _ {2i} E \ cos \ theta / {m} _ {2i} + \ left ({\ omega} ^ 2 -i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) {Q} _ {1i} E \ sin \ theta / {m} _ {1i}} {\ kappa_i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) \ left ({\ omega} ^ 2-i { \ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right)} $$ (3) $$ {a} _ {2i} (t) =\ frac {\ kappa_i ^ 2 { Q} _ {1i} E \ sin \ theta / {m} _ {1i} + \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) {Q} _ {2i} E \ cos \ theta / {m} _ {2i}} {\ kappa_i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ derecha)} $$ (4)La susceptibilidad eléctrica efectiva ( χ ef ), que muestra la relación entre la polarizabilidad total ( P ) de los resonadores plasmónicos y la fuerza del campo eléctrico incidente, entonces se puede expresar en formas de los vectores de desplazamiento como:
$$ {\ Displaystyle \ begin {array} {c} {\ chi} _ {e \ mathrm {ff}, i} =\ frac {P_i ^ 2} {\ varepsilon_0E} =\ frac {Q_ {1i} {a } _ {1i} + {Q} _ {2i} {a} _ {2i}} {\ varepsilon_0E} \\ {} =\ frac {\ left [{\ kappa} _i ^ 2 {Q} _ {1i} {Q} _ {2i} + \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) {Q} _ {1i} ^ 2 \ right] \ sin \ theta / {m} _ {1i} + \ left [{\ kappa} _i ^ 2 {Q} _ {1i} {Q} _ {2i} + \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) {Q} _ {2i} ^ 2 \ right] \ cos \ theta / {m} _ { 2i}} {\ varepsilon_0 \ left [{\ kappa} _i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ derecha) \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) \ right]} \ end {array}} $$ ( 5)Entonces, los espectros de transmisión y absorción simulados pueden ser ajustados por la parte imaginaria de la susceptibilidad. En este artículo, la absorción se define como A =Soy [ χ ef, i ]. Este coeficiente se deriva de la relación de conservación de energía T + A =1; por tanto, tenemos la expresión de la transmisión T =1 - Soy [ χ ef, i ].
Resultados
Excitación de los efectos PIT
Para excitar los efectos PIT, un problema que debe resolverse es cómo diseñar un resonador de modo brillante. Debido al gran desajuste de momento entre las ondas de espacio libre entrantes y las ondas de plasmón, la excitación de los plasmones es uno de los principales desafíos para el uso de plasmones de grafeno. Para terminar con esto, se han propuesto varios enfoques que permiten la excitación de plasmones de grafeno y se han demostrado teórica y experimentalmente. El primer método comúnmente utilizado es modelar la monocapa de grafeno a nanoestructuras coplanares, como nanocintas [25, 54], nanodiscos [55, 56] y círculos [24]. Otro método consiste en construir configuraciones de rejilla en una hoja continua de grafeno, que se logra mediante el uso de rejillas dieléctricas difractivas [51, 57] y las puertas de campo eléctrico [58] para construir rejillas de conductividad local periódicas dependientes de la posición o mediante el uso de rejillas difractivas periódicas. rejillas de ondulación formadas por la propia hoja de grafeno [57, 59]. La razón por la que los plasmones de superficie pueden excitarse en estas estructuras de grafeno es que las nanoestructuras o rejillas pueden proporcionar a las ondas de plasmón un vector de onda recíproco adicional que es necesario para la compensación del desajuste del vector de onda cuando la dirección de polarización es a lo largo de la dirección periódica [51 , 54, 59]. En esta condición, el resonador de grafeno puede funcionar como modo brillante o como modo oscuro. Aquí, proponemos usar tanto los GNR como la hoja de grafeno cargada con rejillas dieléctricas de forma rectangular para trabajar respectivamente como modos brillante y oscuro para construir un sistema PIT, como se muestra en la Fig. 1.
Para explorar el mecanismo del sistema PIT propuesto, se calculan simulaciones numéricas de la configuración que se muestra en la Fig. 1, y los resultados correspondientes para dos ángulos de polarización diferentes se muestran en la Fig. 2. Para el caso con θ =0 °, primero calculamos los resultados para la situación en la que las nanocintas de grafeno inferiores (LGNR) y el grafeno cargado con rejilla dieléctrica superior existen solos. Debido a que la dirección de polarización es perpendicular a los LGNR, los SP pueden excitarse en ellos, lo que da como resultado un pico de absorción principal a 5.327 μm, como la línea azul que se muestra en la Fig. 2a. Por el contrario, los SP en la hoja de grafeno superior no pueden excitarse en esta condición de polarización porque la luz incidente está polarizada en paralelo a las rejillas dieléctricas, lo que resulta en un fuerte desajuste de momento, como lo demuestran las líneas verdes planas en la Fig.2a. En estas situaciones, nos referimos al modo de excitación directa en los LGNR y al modo oscuro en los UGG como LGNRs-0 y UGGs-0, respectivamente, como se muestra en la Fig. 2g y f. Sin embargo, lo interesante aquí es que cuando estas dos capas de grafeno se juntan y se acercan lo suficiente, aparecen dos picos de absorción (caídas de transmisión) a 5.747 μm y 4.917 μm. El que tiene una longitud de onda de resonancia más larga es dominante por absorción que alcanza el 47,16%, mientras que el otro con una longitud de onda de resonancia más corta se caracteriza por un pico de absorción del 35,88%, lo que indica que estos dos modos interactúan muy fuertemente con la luz incidente externa, como se muestra en la Fig. .2a y concluido en la Tabla 1. Estos dos modos se originan de los acoplamientos plasmónicos en fase y fuera de fase entre los dos resonadores. Específicamente, la resonancia del modo brillante en los LGNR debe considerarse como un modo fijo porque se excita directamente con la luz incidente. Sin embargo, la resonancia del plasmón en la capa superior de grafeno no puede excitarse directamente, pero puede acoplarse con los excitados en los LGNR a través de interacciones en fase y fuera de fase. Es la coexistencia de los dos resonadores y sus acoplamientos plasmónicos lo que da como resultado directamente este efecto PIT. Para revelar claramente los mecanismos físicos detrás del origen de los dos modos, mostramos las distribuciones del campo eléctrico en estos dos modos en la Fig. 2h e i. Según la E z distribuciones de campo de componentes, el modo a 5.747 μm muestra una naturaleza de resonancia en fase de la estructura en capas y, por lo tanto, se denomina modo simétrico. El modo a 4.917 μm muestra la resonancia antifase y se denomina modo antisimétrico. Además, la Fig. 2h y yo revelamos claramente la estructura de estos modos:Todos los E z Los componentes muestran una resonancia en modo dipolo caracterizada por un 2 π cambio de fase a lo largo de la dirección de polarización ( x eje) en cada capa de grafeno. Estos dos modos fundamentales eliminan la absorción resonante de los LGNR al mismo tiempo que dan lugar a una ventana de transmisión prominente y dos picos de absorción en el espectro óptico, lo que provoca el efecto óptico llamado PIT (para la conveniencia de la discusión, lo llamamos LGNR-PIT). En la Fig. 2c, también graficamos la fase de transmisión y el tiempo de retardo en los dos picos de absorción, el último alcanza 0.34 ps y 0.36 ps, respectivamente, lo que indica el efecto de ralentización de la luz en el sistema.
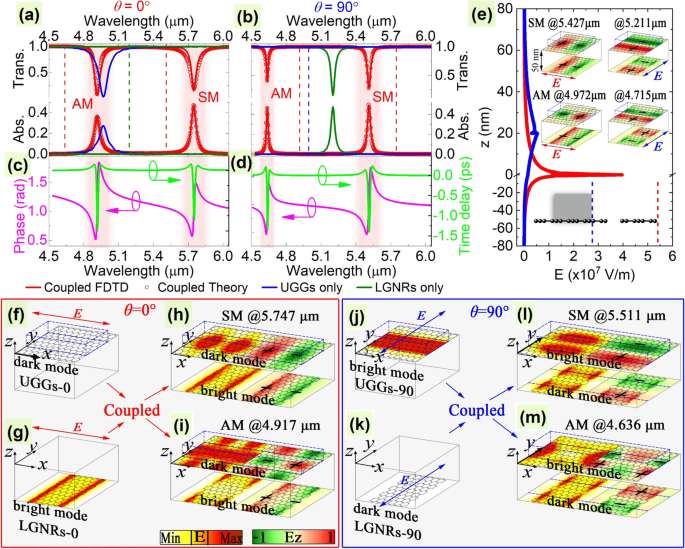
Líneas de transmisión y absorción ( a , b ) y su fase de transmisión (izquierda y eje) y tiempo de retardo (derecha y eje) ( c , d ) del sistema con ángulo de polarización θ =0 ° ( a , c ) y 90 ° ( b , d ), respectivamente. En ( a ) y ( b ), las líneas discontinuas muestran la posición resonante en la otra polarización. Los parámetros de ajuste de las líneas analizadas teóricamente en ( a ) y ( b ) son (en THz) 6,71, 110,07, 2,25, 0,46 y 0,74, y 5,73, 4,13, 72,83, 0,33 y 0,27 para κ i , Q 1i / sqrt ( ε 0 m 1i ), Q 2i / sqrt ( ε 0 m 2i ), γ 1i y γ 2i , respectivamente. Distribuciones espaciales del campo eléctrico para los casos con UGG ( e (línea azul), f , j ) y LGNR ( e (línea roja), g , k) solo a lo largo de la z eje ( e ) y en los planos de grafeno correspondientes ( f , g , j , k ). Distribuciones espaciales del campo eléctrico (paneles izquierdos) y la z correspondiente componente (paneles derechos) del modo simétrico (SM) ( h , @ 5,747 µm; l , @ 5.511 μm) y modo antisimétrico (AM) ( i , @ 4,917 µm; m , @ 4.636 μm) en ángulos de polarización θ =0 ° ( h , yo ) y 90 ° ( l , m ), respectivamente. Las inserciones superiores en e mostrar z componente del campo eléctrico para el caso con d =50 nm, mientras que el inserto inferior representa la posición del campo en el gráfico principal. Los signos "+" y "-" donan las cargas de superficie resonantes; el color más oscuro se refiere a una mayor densidad de carga
Mientras que para el caso de θ =90 °, los SP pueden excitarse en UGG con un pico de absorción principal a 5.202 μm, pero no en los LGNR cuando existen solos, como las líneas verde y azul que se muestran en la Fig. 2b, respectivamente. En estas situaciones, nos referimos al modo de excitación directa en los UGG y al modo oscuro en los LGNR como LGNRs-90 y UGGs-90, respectivamente, como se muestra en la Fig. 2j y k. Sin embargo, cuando estos dos modos están lo suficientemente cerca para acoplarse entre sí, aparecen claramente dos caídas de transmisión (picos de absorción) a 5.511 μm y 4.636 μm con una absorción que alcanza el 49.07% y el 46.46%, respectivamente, lo que significa que las interacciones con las ondas incidentes externas son muy fuertes, como se muestra en la Fig. 2b y concluyen en la Tabla 1. Similar al caso con θ =0 °, el mecanismo físico también puede entenderse considerando los acoplamientos de plasmón en fase y fuera de fase entre las dos capas de grafeno. Como se ilustra claramente en la Fig. 2l ym, la E z Las distribuciones de campo de componentes muestran una resonancia en modo dipolo caracterizada por un 2 π cambio de fase a lo largo de la y eje en cada capa de grafeno y revelan resonancias en fase (modo simétrico) y fuera de fase (modo antisimétrico) en los picos de absorción correspondientes. Son estos dos modos fundamentales los que eliminan la absorción resonante del caso con solo los UGG mientras se genera una ventana de transmisión prominente y dos picos de absorción en el espectro óptico, lo que da como resultado otro PIT (para la conveniencia de la discusión, lo llamamos UGG-PIT ). En la Fig. 2d, también se representan gráficamente la fase de transmisión y el tiempo de retardo en los dos picos de absorción, mostrando el efecto de propagación de la luz más lenta con valores máximos de 0,23 ps y 0,21 ps en el modo simétrico y antisimétrico, respectivamente.
Sin embargo, es importante señalar que aunque las distribuciones de campo en la hoja de grafeno superior del modo antisimétrico en la Fig. 2i ym muestran una apariencia resonante “multipolar”, siguen siendo un modo dipolar ya que las oscilaciones de carga también mantienen la naturaleza de una resonancia en modo dipolo a lo largo de la dirección de polarización. La razón de la apariencia resonante “multipolar” se debe a la fuerte interferencia de campo de los LGNR. Esto puede entenderse considerando el hecho de que el campo de plasmón localizado más fuerte en los GNR con patrón es más pronunciado que el de la hoja continua de grafeno [60], como se muestra en la Fig. 2e. Estas apariencias del modo "multipolar" desaparecerán al configurar el monitor de campo fuera de las dos capas de grafeno o al usar una gran distancia de acoplamiento, por ejemplo, cuando d =50 nm, las apariencias del modo “multipolar” cambiarán a resonancia en modo dipolar puro, como se muestra en las inserciones de la Fig. 2e. Además, también notamos que los acoplamientos de modo entre las dos capas de grafeno son diferentes. Específicamente, para el caso con θ =0 °, el LGNRs-PIT es el resultado del fuerte acoplamiento entre LGNRs-0 y UGGs-0, que resuenan a lo largo de la x dirección. Mientras que para el caso de θ =90 °, el UGGs-PIT es el resultado del fuerte acoplamiento entre UGGs-90 y LGNRs-90, que resuenan a lo largo de la y dirección, como se muestra claramente en la Fig. 2. Por lo tanto, LGNRs-PIT y UGGs-PIT son los efectos de acoplamientos plasmónicos entre diferentes modos que resuenan en diferentes polarizaciones, lo que da como resultado dos efectos PIT diferentes.
Por lo tanto, podemos concluir de la Fig.2 que el LGNRs-PIT (con θ =0 °) y UGGs-PIT (con θ =90 °) son dos efectos PIT diferentes resultantes de dos vías de acoplamiento de modo brillante a oscuro separadas del sistema de grafeno en capas y caracterizadas por la respuesta espectral diferente. Eso significa que podemos cambiar estos dos efectos PIT de uno a otro simplemente cambiando la dirección de polarización de la luz incidente, que es muy diferente del efecto PIT insensible a la polarización (ver la parte de discusión). Además, este efecto PIT conmutable se puede explicar mediante el modelo de dos partículas que se muestra en las Ecs. (1) y (2). Para el caso de θ =0 °, la eficiencia de acoplamiento directo de las UGG al campo incidente es cero (oscuro) mientras que la de los LGNR es la más alta (brillante), como lo demuestra el lado derecho de las ecuaciones. Mientras que para el caso de θ =90 °, viceversa, los UGG se vuelven brillantes mientras que los LGNR son oscuros. Nótese que en ambos casos, la concordancia entre los resultados analíticos obtenidos con la Ec. (5) (representado por círculos rojos en la Fig. 2a, b) y los resultados numéricos (trazados con líneas rojas en la Fig. 2a, b) son casi perfectos. Nuestro modelo analítico predice con mucha precisión no solo las posiciones sino también los valores máximos de las resonancias, como se ve claramente en la Fig. 2. Finalmente, observamos aquí que los resultados presentados aquí son muy diferentes de otros sistemas PIT que se construyen con el mismos resonadores [35, 38]; esto se debe a que no pueden obtener los resultados que se muestran en la Fig. 2 bajo diferentes polarizaciones. Discutiremos las diferencias más a fondo en la parte de discusión.
Sintonización geométrica de PIT
Hemos demostrado que los acoplamientos de campo cercano entre los modos brillante y oscuro dan como resultado dos efectos PIT dependientes de la polarización; por lo tanto, los parámetros que afectan en gran medida las resonancias del modo oscuro y brillante, así como la fuerza de acoplamiento entre ellos, pueden tratarse como un parámetro ajustable para los efectos PIT. Primero realizamos estudios paramétricos para el caso con θ =0 ° cambiando el ancho ( W r ) de los LGNR y los anchos ( W d ) de las UGG de 20 a 100 nm, y muestran los resultados en la Fig. 3a yc, respectivamente. Debido a que los LGNR se acoplan directamente con la luz incidente y funcionan como modo brillante en estas condiciones, cualquier cambio en sus dimensiones afecta directamente a toda la respuesta plasmónica del sistema. Por ejemplo, cuando W r es muy pequeño, por ejemplo, 20 nm, la eficiencia de acoplamiento con la luz incidente es muy débil debido a la baja tasa de ocupación de los GNR [14, 51], lo que da como resultado una baja absorción del modo antisimétrico y especialmente el modo simétrico del sistema PIT, como puede verse en la línea de absorción de W r =20 nm en la Fig. 3a. Como otro ejemplo, cuando W r es lo suficientemente grande, y especialmente cuando alcanza su máximo de 100 nm (es decir, cuando el LGNR es una capa completa de grafeno), ninguno de los dos resonadores puede acoplarse con el campo externo y, por lo tanto, el LNGR-PIT desaparece. En particular, las absorciones de los dos modos muestran los valores más altos simultáneamente cuando W r es de alrededor de 50 nm. A diferencia del modo brillante, las variaciones de ancho de DG ( W d ) en la capa superior de grafeno para el modo oscuro solo puede sintonizar las posiciones resonantes y las absorciones del modo simétrico y antisimétrico dentro de los límites, mientras que no puede eliminar o incluso afectar significativamente la alta eficiencia de acoplamiento con las ondas externas, como se muestra en la Fig. 3c. En realidad, incluso cuando las rejillas dieléctricas se eliminan o se convierten en una capa dieléctrica completa ( W d =100 nm), los LGNR aún pueden acoplarse con la hoja de grafeno superior, como se demostró mediante un caso bidimensional descrito en un trabajo anterior [36], donde solo se permite que exista un efecto PIT.
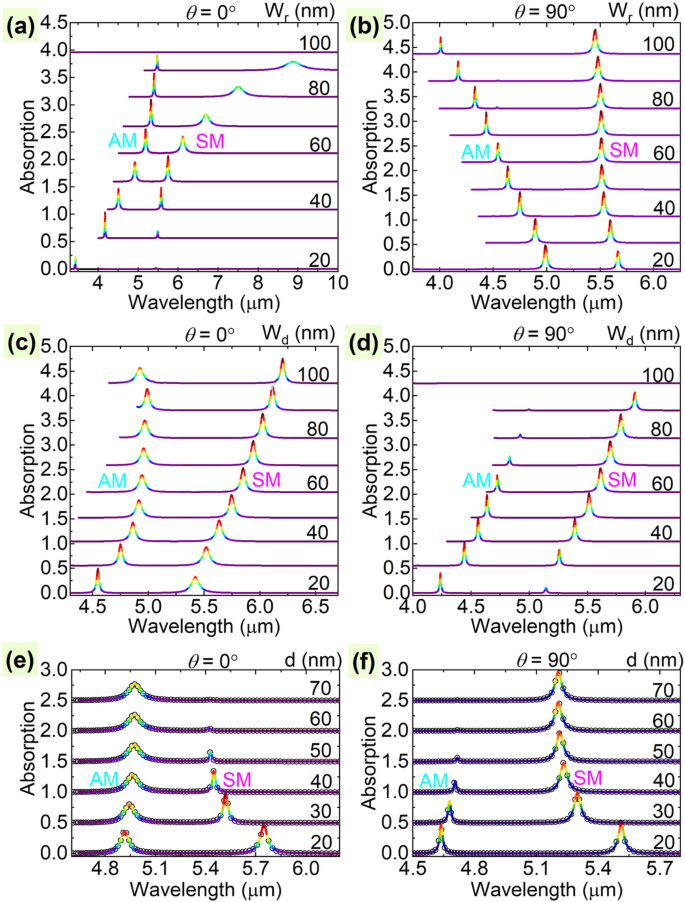
Espectros de absorción del sistema PIT en la escala de longitud de onda en función de ( a ), ( b ) el ancho de la cinta W r de LGNR; ( c , d ) el ancho de DG W d de UGG; y ( e , f ) la distancia de separación d entre las dos capas de grafeno con un paso de 10/20 nm en ángulos de polarización de θ =0 ° ( a , c , e ) y 90 ° ( b , d , f ), respectivamente. En ( a - f ), el color rojo más intenso en las líneas continuas denota una absorción más fuerte. Tenga en cuenta que algunas de las líneas se cortan para evitar distracciones de otros picos de absorción de orden superior. En ( e ) y ( f ), las curvas sólidas y las ojeras presentan los resultados numéricos y teóricos, respectivamente. SM y AM se refieren al modo simétrico y al modo antisimétrico, respectivamente
Sin embargo, para el caso de θ =90 °, los resultados contrastan con el caso de θ =0 ° porque los LGNR funcionan como un modo oscuro mientras que los UGG funcionan como un modo brillante. En detalle, el cambio del ancho LGNR W r solo modula las posiciones resonantes y las absorciones máximas del modo simétrico y del modo antisimétrico, mientras que no puede extinguir la existencia de los dos modos, como se muestra en la Fig. 3b. Esto se debe a que los LGNR funcionan como un modo oscuro en esta condición de polarización. En la condición con W r =100 nm, el sistema se convierte en una hoja de grafeno cargada con DG que se acopla con otra hoja de grafeno, que es similar a un sistema PIT simple bidimensional informado anteriormente en otro estudio [34]. Sin embargo, el cambio de las rejillas dieléctricas superiores tendrá un gran impacto en la respuesta óptica del sistema PIT, ya que la hoja de grafeno superior funciona como un modo brillante en esta condición, que es muy similar al caso cuando se cambia W r con θ =0 °, como se muestra en la Fig. 3d. En general, podemos concluir de la Fig. 3a-d que la sintonización del modo brillante afectará en gran medida la apariencia e incluso la existencia de las UGGs-PIT, como se demuestra en las Fig. 3a yd, mientras que el cambio de la el modo oscuro solo puede cambiar las posiciones resonantes y las fuerzas relativas del modo simétrico y el modo antisimétrico en el UGGs-PIT, como se muestra en las Fig. 3b y c.
Otro parámetro que afecta mucho a los efectos PIT es el espacio d entre los dos resonadores de grafeno. A medida que arreglamos los anchos de los GNR y las rejillas dieléctricas y luego aumentamos d , the interaction strength between the two graphene resonators decreases monotonically for both polarization angles due to the fast decreasing plasmonic field in the normal direction of the graphene surface [35, 61]. As a result, the symmetric mode and the antisymmetric mode are respectively extinguished for the case with θ =0° and θ =90° at large coupling distance, e.g., d> 70 nm, as shown in Fig. 3e and f. As it is known that when the bright and dark modes are far beyond the decay length of the evanescent field of each other, these two modes are uncoupled, and therefore, only the bright mode exists. At that point, we can conclude from Fig. 3e and f that the symmetric mode and antisymmetric mode of the PIT respectively originate from the UGGs and LGNRs, as they remain at large layer distance. Note that the PIT effects at different coupling strengths match well with the two-particle model, as the simulated and analytically predicted results are in excellent agreement, as can be seen in Fig. 3a and b, where the solid curves are gotten from FDTD, and the dark circles are from the two-particle model.
Electrical Tunability of PIT
One of the major advantages of graphene-based plasmonic devices is their dynamic and broadband tunability, which can be realized by electrostatic gating techniques [61, 62]. This intriguing property allows us to electrically change the Fermi energy of graphene and, thus, to actively modulate the transmission window of the proposed PIT systems to work at different wavelengths without reconstructing the geometrical structure [24, 25]. By applying different bias voltages with a field-effect transistor structure, researchers have experimentally achieved the dynamical tune of the Fermi energy level from 0.2 to 1.2 eV [63]. The simulated absorption spectra shown in Fig. 4 confirms the broadband and dynamic tunability of the proposed PIT device. For the given geometrical parameters, the plasmon wavelengths of the symmetric mode and antisymmetric mode of the LGNRs-PIT (UGGs-PIT) can be tuned from 4.977 to 9.953 μm and 4.259 to 8.520 μm (from 4.775 to 9.551 μm and 4.015 to 8.033 μm) when the Fermi level is modulated from 0.8 to 0.2 eV, respectively, as the solid and dash-dotted lines shown in Fig. 4a and b. This dynamic tunability will greatly facilitate the design and practical application of the proposed PIT device.
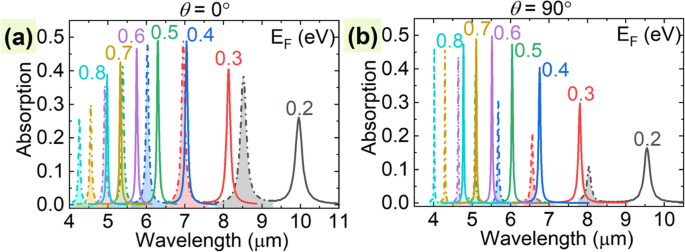
Absorption spectra of the symmetric mode (solid lines) and antisymmetric mode (dash-dotted lines) of the proposed PIT system with different Fermi energy levels of graphene at polarization angles of θ =0° (a ) and 90° (b ), respectivamente
Applications
In the previous parts, we have made clear how the LGNRs couple with the UGGs and further result in the polarization-dependent PIT effects, and demonstrated how the geometrical and electrical parameters affect the couplings. In this part, we will demonstrate our proposal can be used as selective refractive index sensors and dual-band perfect absorbers.
Considering that the PIT effect is determined by both the bright and dark mode resonances, what brings the change to these two modes will directly alter the symmetric mode and antisymmetric mode in the PIT window. Therefore, the induced symmetric mode and antisymmetric mode are highly sensitive to the local dielectric environment, which can be applied to design refractive index sensors [64]. In our design, both the regions above the UGGs (with refractive index n 0 ) and below the LGNRs (with refractive index n 2 ) can be thought of as the sensing regions. To calculate the sensitivities, we define S =Δλ/ Δn , which specifies the plasmon wavelength (λ ) shift per refractive index unit (RIU). We assume the refractive indexes of the materials as n 1 =2.0 and n 0 =n 2 =n 3 =1.3 (except the cases when n 0 or n 2 is working as the sensing regions with the range changing from 1.0 to 1.1).
Firstly, when tuning the width of the GNRs (W r ), we find that when the sensing region is alongside the bright mode (that are sensing region n 0 with θ =90° and sensing region n 2 with θ =0°), the sensitivity of the symmetric mode S SM gets bigger at wider ribbon width (see the solid blue lines in Fig. 5b, c). Especially, S SM can reach 4 μm/RIU for the case with θ =0° in sensing region n 2 . Secondly, for the case with increasing DG width (W d ), both the sensitivity of the symmetric mode S SM and antisymmetric mode S AM decrease in most cases. Finally, as for the coupling distance d between the two layers, it is found that S SM decreases while that of the antisymmetric mode increases for both of the polarization angles (see the solid and dash-dotted dark lines in Fig. 5). Considering that the antisymmetric mode will disappear under large coupling distance at the polarization angle of θ =90° (see Fig. 3f), the antisymmetric mode for the situation with θ =0° is more suitable to work as a sensor at a larger distance. Generally, the sensitivities of the symmetric mode and antisymmetric mode of the LGNRs-PIT and UGGs-PIT are respectively comparable to each other, as can be concluded by comparing Fig. 5a with 5b, and Fig. 5c with 5d, respectively. Besides, it is also found that the sensitivities for the cases with sensing regions alongside the bright and dark modes do not show a big difference, as can be seen by comparing Fig. 5a with 5d (alongside the dark mode), and Fig. 5b with 5c (alongside the bright mode). However, the sensitivities of the case with the sensing region under the LGNRs are obviously higher than that of the case with the sensing region above the UGGs, as they are shown by comparing Fig. 5a and b with Fig. 5c and d. This is because the sensitivity is directly related to the localized plasmonic field [64], and the local plasmonic field in the cutting-edge nanoribbons is generally stronger than the continuous edge-free graphene dielectric gratings [60].
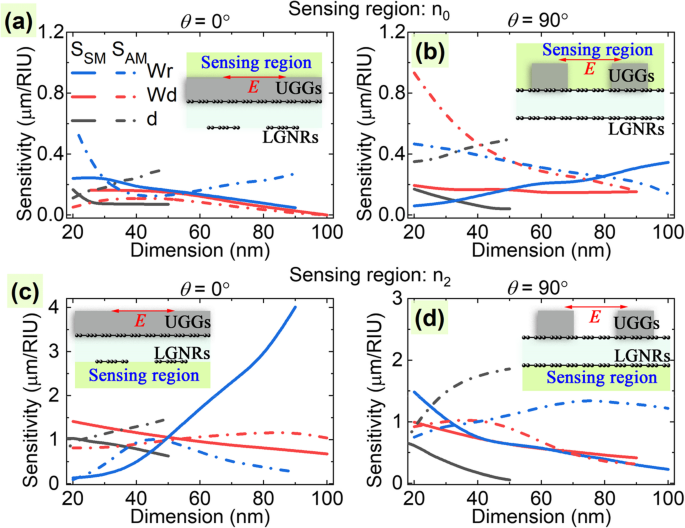
Refractive index sensitivities of the symmetric mode (SSM , solid lines) and antisymmetric mode (SAM , dash-dotted lines) in the sensing regions of n 0 ( a , b ) y n 2 ( c , d ) as functions of the ribbon width W r of LGNRs, the DG width W d of UGGs, and the separation distance d between the two graphene layers at polarization angles of θ =0° (a , c ) and 90° (b , d ), respectivamente. The inserts show the location of the sensing region
Besides working as a refractive index sensor, the proposed system can also be further designed as a perfect absorber. To achieve this, we can add a metallic substrate below the LGNRs and assume the refractive indexes of the materials as n 1 =2.0 and n 0 =n 2 =n 3 =1.3. With the existence of the metallic substrate, the dielectric layer between the LGNRs and metallic mirror forms a Fabry-Perot cavity, which can increase the interaction of incidence with graphene layers and further increase the absorptivity of the two modes. For the LGNRs-PIT case with θ =0°, we find that perfect absorptions with absorptivity> 96% of the symmetric mode and antisymmetric mode can be achieved simultaneously when the metallic substrate is with a 3.0-μm distance below the LGNRs, as shown in Fig. 6a and c. We also find that our proposal has good robustness to the doping level of graphene, as shown in Fig. 6a. The absorptivity of the two modes is> 90% when the Fermi energy level of graphene ranges from 0.58 to 0.66 eV. Besides the doping level of graphene, the perfect absorptions also show good tolerance to the polarization angle:The absorptivity of the two modes can keep at a high level (>90%) even the polarization angle ranges from − 17 to 17°. The robustness to the parameters is good for the practical design of the absorber.
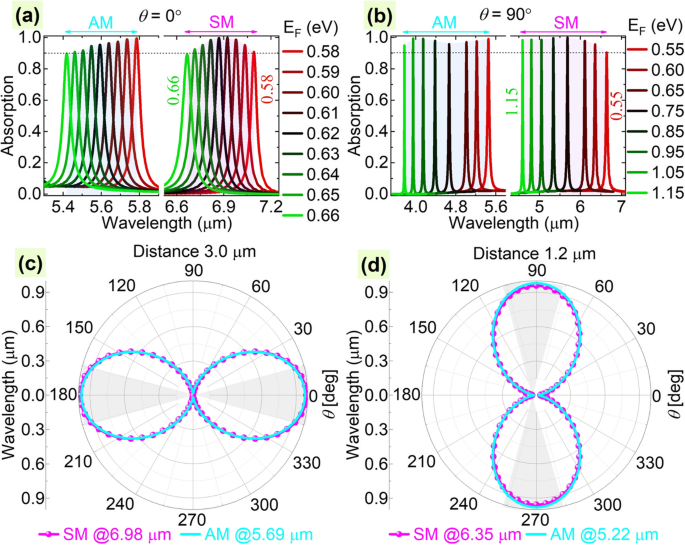
Absorption spectra with different Fermi energy levels of graphene at polarization angles of θ =0° (a ) and 90° (b ) for the cases with a metal substrate below the LGNRs with a distance of 3.0 μm (a , c ) and 1.2 μm (b , d ), respectivamente. ( c , d ) Absorption maxima as functions of θ . SM and AM refer to the symmetric mode and antisymmetric mode, respectively
To achieve the perfect absorption for the UGGs-PIT case with θ =90°, we need to set the metallic substrate with a 1.2-μm distance below the LGNRs. It is found that perfect absorptions with absorptivity> 95% of the symmetric mode and antisymmetric mode can be achieved simultaneously, as shown in Fig. 6b and d. Similar to the LGNRs-PIT case, it also found that the perfect absorptions show good tolerance to the polarization angle ranging from − 15 to 15° with absorptivity of the two modes> 90% (see Fig. 6d). More notably, the proposed absorber for the UGGs-PIT case shows much bigger robustness to the doping level of graphene, as plotted in Fig. 6b. It is found that the absorptivity of the two modes is> 90% even the Fermi energy level of graphene ranges from 0.55 to 1.15 eV. Considering that the Fermi level of graphene can be dynamically tuned by an external gate voltage, the designed structure can be thought of as active dual-band perfect absorber with a working wavelength of the symmetric mode (antisymmetric mode) ranging from 4.59 to 6.64 μm (3.77 to 5.45 μm).
Discussions
In this part, we discuss the advantages and differences of the proposed structure with other similar structures. To this end, we first calculated the plasmon resonant wavelengths for the cases with only the GNRs and only the dielectric grating-loaded graphene, as shown in Fig. 7a. It shows that the plasmon wavelengths have different dependencies on the width of the resonator. Besides, the inserts show the resonant property of the modes:For GNRs, the plasmonic fields are mainly localized on the edge of the GNR, while for the case with graphene sheet attached with dielectric gratings, the plasmonic fields are mainly concentrated on the grating area. Previous studies have shown that the field distributions and the distance between the resonators will greatly affect the plasmonic couplings [35, 65] and, therefore, the spectral response of the coupled system. That is to say, in our cases, the couplings from the LGNRs to the upper dielectric gratings are different from the other way coupled from the upper dielectric gratings to the LGNRs. Therefore, we obtain the results shown in Fig. 7b that even when the plasmon wavelengths of the two resonators are the same when they exist alone, they will also lead to two distinct PIT effects no matter what they work as bright or dark modes. To show more clearly the advantage of our design, we plot the resonant mode positions of the PIT effects for different geometrical parameters in Fig. 7c and d. They clearly demonstrate that there are always two distinguishable PIT effects for the two polarization directions, even when the geometrical parameters are the same.
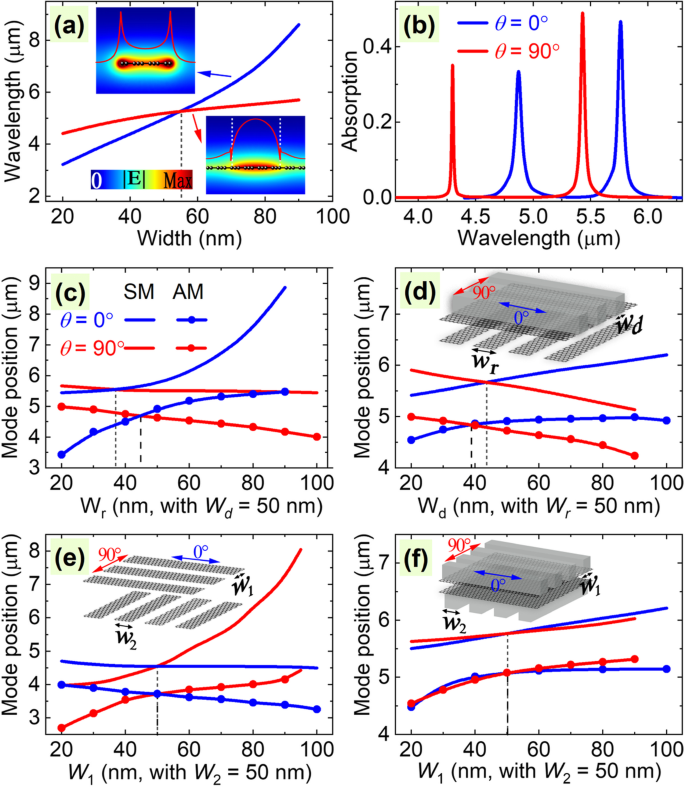
( a ) Plasmon wavelengths of the cases with only the GNRs and only dielectric grating-loaded graphene sheet for different ribbon and grating width. The inserts show the field distribution of the modes. ( b ) Absorption spectra for different polarization angles of GNR and dielectric grating-loaded graphene-coupled system with their width of 54 nm. ( c - f ) Resonant positions of the two PIT peaks at different polarization angles for different systems. The inserts show the corresponding structures
However, one may want to know why the proposed structure is not designed with the same resonators, such as perpendicular GNRs and dielectric grating-loaded graphene, as it has been reported in the previous studies [35, 38]. To explain this, we have plotted the resonant positions of the two modes in the PIT effects for the structures with pure GNRs and dielectric grating-loaded graphene resonators in Fig. 7e and f, respectively. It is found that when the two layers of resonators are designed with the same geometrical parameters, there is only one PIT effect for all the polarization directions, which means the PIT effect becomes indistinguishable from the absorption spectrum. This is because the couplings between the two layers of resonators are equivalent due to the same field distribution of the plasmon modes. That is to say, the polarization-independent PIT effects of the structures shown in the insert of Fig. 7e and f depend on the particular choice of the geometrical parameters. Whereas, on the contrary, the design in this paper to achieve two switchable PIT effects is not dependent on the particular choice of the geometrical parameters, which can guarantee the existence of the two switchable PIT effects.
Conclusión
In this paper, both advanced simulations and theoretical analyses are combined to investigate switchable PIT effects in two graphene layers formed by GNRs coupled with a dielectric grating-loaded graphene layer. Thanks to the crossed nanoribbon and grating directions, both the GNRs and the dielectric gratings can operate as either the bright or the dark mode depending on the polarization direction. The incident light under these two polarization directions introduces two different bright to dark mode coupling pathways within the two resonators, resulting in two switchable PIT effects. Geometrical parameters, such as graphene nanoribbon width, dielectric grating width, layer distance, and graphene Fermi level, are used to study the physical mechanism and the performance of the proposed PIT effect. Additionally, the proposed concepts are examined by applying a two-particle model, showing outstanding agreement with the numerical results. The proposed methods provide a general approach to achieving switchable PIT effects in distinct resonator-coupled system and can advance the applicability and versatility of PIT-based plasmonic sensing platforms and active dual-band perfect absorbers.
Disponibilidad de datos y materiales
Todos los datos que respaldan las conclusiones de este artículo se incluyen en el artículo.
Historial de cambios
Abreviaturas
- FDTD:
-
Dominio del tiempo de diferencia finita
- GNR:
-
Graphene nanoribbons
- LGNRs:
-
Lower graphene nanoribbons
- PIT:
-
Plasmonically induced transparency
- UGGs:
-
Upper graphene gratings
Nanomateriales
- Control de no linealidad dual de las propiedades de modo y dispersión en la guía de ondas plasmónica de grafeno-dieléctrico
- Transparencia inducida por plasma sintonizable dinámicamente en un sistema de guía de ondas acoplado por nanocavidad asimétrico basado en grafeno en chip
- Alto rendimiento fotocatalítico de dos tipos de fotocatalizadores compuestos de TiO2 modificado con grafeno
- RGO y redes de grafeno tridimensionales co-modificadas TIM con alto rendimiento
- Análisis de mapeo Raman de resonadores de microanillos de silicio integrados con grafeno
- Efectos sinérgicos de nanopartículas de Ag / BiV1-xMoxO4 con actividad fotocatalítica mejorada
- Evaluación de estructuras de grafeno / WO3 y grafeno / ceO x como electrodos para aplicaciones de supercondensadores
- Aerogel de grafeno / polianilina con superelasticidad y alta capacitancia como electrodo supercondensador altamente tolerante a la compresión
- Nanocomposites a base de óxido de grafeno decorados con nanopartículas de plata como agente antibacteriano
- Ángulos de contacto del aceite en un sistema de agua-decano-dióxido de silicio:efectos de la carga superficial
- Efectos de los parámetros de sonicación de la punta sobre la exfoliación en fase líquida de grafito en nanoplaquetas de grafeno



