Transparencia inducida por plasma sintonizable dinámicamente en un sistema de guía de ondas acoplado por nanocavidad asimétrico basado en grafeno en chip
Resumen
Se ha propuesto y modelado una nanoestructura plasmónica en chip basada en grafeno compuesta por una guía de onda de bus plasmónica acoplada lateralmente con nanocavidades rectangulares y en forma de U utilizando el método de elementos finitos en este artículo. Se ha investigado la capacidad de sintonización dinámica de las ventanas de transparencia inducida por plasmón (PIT). Los resultados revelan que los efectos PIT se pueden ajustar modificando el potencial químico de las nanocavidades y la guía de onda del bus plasmónico o variando los parámetros geométricos, incluida la ubicación y el ancho de la nanocavidad rectangular. Además, la nanoestructura plasmónica propuesta se puede utilizar como un sensor de índice de refracción plasmónico con una sensibilidad de detección de 333,3 nm / unidad de índice de refracción (RIU) en el pico de transmisión PIT. El efecto de luz lento también se realiza en el sistema PIT. La nanoestructura propuesta puede allanar un nuevo camino hacia la realización de dispositivos nanofotónicos integrados en chip basados en grafeno.
Antecedentes
La transparencia inducida por plasmón (PIT), que es un fenómeno novedoso análogo al efecto de transparencia inducida electromagnéticamente (EIT) que genera una ventana de transparencia nítida dentro de un amplio espectro de absorción [1], ha atraído una gran atención debido a sus posibles aplicaciones en una amplia gama de campos, como luz lenta [2, 3], conmutación óptica [4], almacenamiento de luz [5] y detección de alta sensibilidad [6, 7]. Los dispositivos basados en PIT se pueden realizar con una huella ultracompacta debido a la gran capacidad de mejora del campo local y la superación del límite de difracción clásico de la luz proporcionada por los polaritones de plasmón de superficie (SPP) [8, 9]. Se han propuesto una variedad de diseños para lograr el efecto PIT en nanoestructuras plasmónicas, incluidos sistemas de resonadores acoplados [10,11,12,13], estructuras de cristal fotónico [14, 15] y estructuras de metamateriales [16, 17]. Sin embargo, la mayoría de estas estructuras que muestran el efecto PIT apenas se pueden sintonizar a menos que se modifiquen los parámetros geométricos de las estructuras, que en gran medida limitan el control activo de las ventanas PIT y degradan la calidad.
El grafeno, una monocapa de átomos de carbono dispuestos en una red de panal bidimensional (2D) [18], muestra un gran potencial para desarrollar dispositivos optoelectrónicos altamente eficientes debido a sus excepcionales propiedades eléctricas y ópticas, incluida la capacidad de confinamiento extremo [19,20, 21], sintonía dinámica y pérdidas por amortiguación relativamente bajas [22, 23]. Particularmente, la conductividad superficial del grafeno puede ajustarse dinámicamente por potencial químico a través de voltaje de puerta externa o dopaje químico [24, 25], lo que hace que el grafeno sea un candidato prometedor para diseñar PIT sintonizable mientras los parámetros geométricos son fijos. Debido a estas características extraordinarias en comparación con las de los metales nobles convencionales, se ha realizado una amplia gama de investigaciones para realizar la PIT basada en grafeno, como los fenómenos de PIT en la guía de ondas de grafeno acoplada al resonador de anillo de grafeno [26, 27] y los efectos de PIT en un Guía de ondas de nanocintas a base de grafeno junto con una estructura de resonador rectangular de grafeno [28, 29]. Sun y col. estudiaron la estructura de doble capa de grafeno con patrones periódicos separados por una capa dieléctrica en el rango de frecuencia de terahercios, donde se han logrado las respuestas PIT multiespectrales [30]. Además, los efectos de PIT sintonizables se realizan en las nanobandas de grafeno combinadas periódicamente y se describen analíticamente con el modelo de oscilador de Lorentz acoplado [31, 32]. Sin embargo, la mayoría de los trabajos anteriores se referían a los resonadores de grafeno, acoplados a un sistema de guía de ondas de grafeno monocapa o de nanocintas de grafeno, y sistemas de nanobandas de grafeno con luz incidente normal. Hubo muy pocos o incluso ningún estudio sobre el fenómeno de transparencia inducido plasmónicamente en una hoja de grafeno con potenciales químicos variantes localmente. Además, en comparación con la luz incidente normal, la propagación en el plano tiene ventajas abrumadoras para la integración en el chip.
Motivados por los estudios fundamentales anteriores, en este artículo proponemos una nanoestructura plasmónica basada en grafeno compuesta por una guía de onda de bus plasmónica acoplada lateralmente a una nanocavidad en forma de U y una nanocavidad rectangular en la misma monocapa de grafeno. El software comercial COMSOL Multiphysics basado en el método de elementos finitos (FEM) se utiliza para explorar la transmisión y las respuestas electromagnéticas de nuestros diseños. Los resultados de la simulación revelan que el fenómeno PIT se observa en nuestra nanoestructura plasmónica propuesta. Además, la ventana PIT se puede ajustar de forma eficaz variando los potenciales químicos de las nanocavidades y la guía de ondas del bus plasmónico. Además, se introduce una teoría del modo acoplado (CMT) para explicar las características de transmisión del fenómeno PIT. Por último, se estudia un sensor de índice de refracción plasmónica basado en la nanoestructura plasmónica propuesta. La sensibilidad de detección de 333,3 nm / unidad de índice de refracción (RIU) se logra en el pico de transmisión PIT. Además, se realiza el efecto de luz lento con retardo de grupo superior a 1 ps. Esta nueva nanoestructura plasmónica propuesta puede ofrecer una nueva forma de realizar la integración del dispositivo plasmónico de alta densidad en chip basado en grafeno en una monocapa de grafeno.
Métodos
En aras de la simplicidad, la estructura propuesta está modelada por una monocapa de grafeno suspendida con variación local del potencial químico para formar la guía de ondas de bus correspondiente y los nanoresonadores. La Figura 1a muestra la configuración esquemática y los parámetros geométricos de una nanocavidad en forma de U acoplada directamente a una guía de ondas de bus plasmónico. La guía de ondas acoplada con nanocavidad en forma de U con un potencial químico de μ c2 está rodeado por la misma hoja de grafeno con un potencial químico de μ c1 . El ancho de la guía de ondas del bus plasmónico d es de 20 nm. El ancho y alto de la nanocavidad en forma de U son W U =150 nm y L U =120 nm respectivamente. El modelado teórico exacto de dicha estructura requiere un cálculo tridimensional (3D), que consume mucho tiempo y memoria. Para resolver este problema, el método de índice efectivo ha sido utilizado por muchas publicaciones [33,34,35], y el índice de refracción de la estructura es reemplazado por el índice efectivo de modos guiados, que se define por la relación entre la constante de propagación y el número de onda en el espacio libre. En nuestra estructura, la hoja de grafeno se trata como una película ultrafina que se caracteriza por un índice efectivo definido como n ef = β / k 0 , donde k 0 =2 π / λ es el número de onda en el espacio libre. La constante de propagación β del modo SPP guiado compatible con grafeno monocapa se escribe como [36, 37]
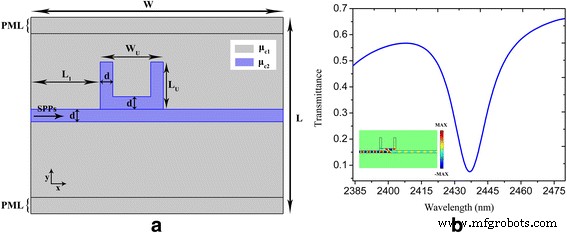
a, b La configuración esquemática y los parámetros geométricos de un sistema de guía de ondas acoplado por nanocavidades en forma de U y la transmitancia espectral correspondiente, respectivamente. El recuadro en b muestra el campo eléctrico ( E años ) distribución a una longitud de onda de 2437 nm. Los parámetros se establecen como W =800 nm, L =620 nm, d =20 millas náuticas, ancho U =150 nm, L U =120 nm, L 1 =220 nm, τ =1 ps, μ c1 =0,3 eV y μ c2 =0,9 eV. Las capas perfectamente combinadas ( PML ) con un ancho de 50 nm se implementan en la parte superior y abajo del dominio de cálculo para eliminar reflejos no deseados del límite del dominio
$$ \ beta ={k} _0 \ sqrt {1 - {\ left (\ frac {2} {\ sigma _ {\ mathrm {g}} \ sqrt {\ mu_0 {\ mu} _ {\ mathrm {r}} / {\ varepsilon} _0 {\ varepsilon} _ {\ mathrm {r}}}} \ right)} ^ 2,} $$ (1)donde μ 0 y ε 0 representan la permeabilidad y permitividad del vacío, respectivamente, y μ r y ε r representan la permeabilidad relativa y la permitividad relativa respectivamente. La conductividad superficial del grafeno σ g compuesto por las transiciones de electrones entre bandas σ entre y la dispersión de electrones y fotones dentro de la banda σ intra viene dada por la fórmula de Kubo [38, 39]
$$ {\ sigma} _ {\ mathrm {g}} ={\ sigma} _ {\ mathrm {intra}} + {\ sigma} _ {\ mathrm {inter}} $$ (2)Con
$$ {\ sigma} _ {\ mathrm {intra}} =\ frac {- i {e} ^ 2 {k} _ {\ mathrm {B}} T} {\ pi {\ hslash} ^ 2 \ left ( \ omega - i / \ tau \ right)} \ left [\ frac {\ mu _ {\ mathrm {c}}} {k _ {\ mathrm {B}} T} +2 \ ln \ left (1+ \ exp \ izquierda (- \ frac {\ mu _ {\ mathrm {c}}} {k _ {\ mathrm {B}} T} \ derecha) \ derecha) \ derecha] $$ (3) $$ {\ sigma} _ {\ mathrm {inter}} =\ frac {- i {e} ^ 2} {2 h} \ ln \ left [\ frac {2 \ left | {\ mu} _c \ left | - \ hslash \ left (\ omega - i / \ tau \ right) \ right. \ right.} {2 \ left | {\ mu} _c \ left | + \ hslash \ left (\ omega - i / \ tau \ right) \ right. \ right.} \ derecha] $$ (4)donde μ c es el potencial químico del grafeno, ω es la frecuencia angular del plasmón, ћ es la constante de Planck reducida, e es la carga del electrón, k B es la constante de Boltzmann, T es la temperatura, ℏ =h / 2 π es la constante de Planck reducida, y τ es el tiempo de relajación del impulso electrónico. Específicamente, el potencial químico del grafeno se puede ajustar mediante el dopaje químico o la compuerta eléctrica [25, 26]. Mikhailov y col. han demostrado experimentalmente que la densidad de portadores en una hoja de grafeno tan alta como 10 14 cm −2 se había logrado, lo que condujo a un potencial químico de 1 a 2 eV a una temperatura por debajo de 250 K [40]. Además, se ha demostrado que el grafeno suspendido de alta calidad con una movilidad de corriente continua de hasta 10 5 cm 2 V −1 s −1 se puede obtener, que corresponde a τ > 1,5 ps [41]. En este artículo, tanto el tiempo de relajación como el potencial químico que establecemos son lo suficientemente conservadores como para garantizar la confiabilidad de nuestro estudio numérico.
Resultados y discusión
A medida que la onda SPP pasa a través de la nanocavidad en forma de U acoplada lateralmente que se muestra en la Fig. 1a, la energía se acopla en la nanocavidad. Se obtiene un valle de transmisión profundo en la longitud de onda de resonancia debido a la interferencia destructiva entre la onda incidente y la energía que se escapa de la nanocavidad [12, 13]. La Figura 1b traza el espectro de transmisión de una nanocavidad en forma de U acoplada directamente a una guía de onda de bus plasmónico con τ =1 ps, μ c1 =0,3 eV y μ c2 =0,9 eV. Se logra una caída pronunciada con transmitancia inferior a 0,1 a la longitud de onda de resonancia de 2437 nm. El recuadro de la Fig. 1b muestra la distribución del campo eléctrico correspondiente en la longitud de onda de resonancia, donde se puede ver que casi ningún SPP se propaga a través de la guía de ondas plasmónica. La figura 2a muestra los espectros de transmitancia con tiempo de relajación variado τ =0,6, 0,8 y 1 ps, donde se puede ver que se logra un mayor contraste de transmisión cuando aumenta el tiempo de relajación. Esto se atribuye a la reducción de la absorción óhmica de los plasmones cuando aumenta el tiempo de relajación del momento electrónico [39]. La transmitancia calculada de un sistema de guía de ondas acoplado a nanocavidades en forma de U para diferentes potenciales químicos μ c2 se presenta en la Fig. 2b. El tiempo de relajación τ y potencial químico μ c1 se mantienen constantemente en 1 ps y 0,3 eV respectivamente. Se puede ver que las ubicaciones de las inmersiones se ajustan dinámicamente a través del potencial químico variado de la nanocavidad y la guía de ondas del bus. Las longitudes de onda centrales de las caídas son 2455, 2445 y 2437 nm con μ c2 =0,89, 0,895 y 0,9 eV respectivamente.
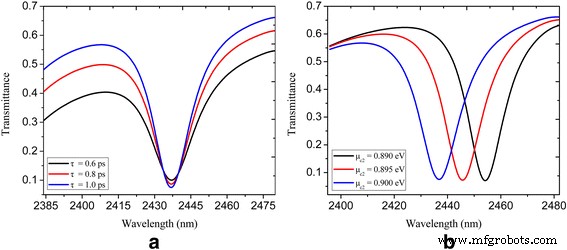
Transmitancia espectral de un sistema de guía de ondas acoplado a nanocavidades en forma de U que se muestra en la Fig. 1: a con τ =0,6, 0,8 y 1 ps; μ c1 =0,3 eV; y μ c2 =0,9 eV; b con μ c2 =0,89, 0,895 y 0,9 eV; μ c1 =0,3 eV; y τ =1 ps
Según CMT [12, 42, 43], la transmitancia espectral del sistema que soporta un modo resonante de frecuencia ω 0 se puede escribir como
$$ T =\ frac {{\ left (\ omega - {\ omega} _0 \ right)} ^ 2 + {\ left (1 / {\ tau} _i \ right)} ^ 2} {{\ left (\ omega - {\ omega} _0 \ right)} ^ 2 + {\ left (1 / {\ tau} _i + 1 / {\ tau} _e \ right)} ^ 2} $$ (5)donde 1 / τ i y 1 / τ e representan la tasa de desintegración de la pérdida intrínseca en la nanocavidad y la potencia que escapa a través de la guía de ondas del bus plasmónico, respectivamente. Obviamente, la transmitancia mínima T min =(1 / τ i ) 2 / (1 / τ i + 1 / τ e ) 2 se puede lograr cuando la frecuencia de la luz incidente ω es igual a la frecuencia de resonancia ω 0 . Como el 1 / τ e es mucho más que 1 / τ i , se puede obtener una caída de transmisión cercana a cero, lo que concuerda bien con los resultados de la simulación.
Para obtener efectos PIT, agregamos una nanocavidad rectangular basada en la nanoestructura plasmónica que se muestra en la Fig. 1. En la Fig. 1 se muestra esquemáticamente una nanoestructura plasmónica basada en grafeno compuesta por una guía de onda de bus plasmónica acoplada lateralmente a nanocavidades rectangulares y en forma de U. .3a. Existe un fuerte acoplamiento entre las dos nanocavidades cuando están conectadas a través de la guía de ondas del bus plasmónico. La interferencia destructiva entre dos vías de excitación resonante relacionadas con las nanocavidades rectangulares y en forma de U genera el fenómeno PIT [10, 11]. Como se muestra en la Fig. 3b, apareció un pico de transmisión agudo (aumentado de 0,06 a 0,44) en la banda prohibida de transmisión mostrada en la Fig. 1b, lo que implica la formación de la ventana PIT. La longitud de onda central de la ventana PIT es 2437 nm, que es exactamente la ubicación de la longitud de onda central de la caída de transmisión que se muestra en la Fig. 1b. La amplia resonancia de la nanocavidad en forma de U se divide en dos modos de resonancia:uno está desplazado al azul mientras que el otro está desplazado al rojo [12, 13]. La Figura 3c-e muestra las distribuciones del campo eléctrico de los modos resonantes a 2408, 2437 y 2457 nm, respectivamente. Podemos ver que la distribución del campo eléctrico en las nanocavidades está en fase con la distribución del campo eléctrico en las guías de onda del bus plasmónico a 2437 nm, lo que significa que la luz incidente y la luz que escapa hacia la guía de onda del bus plasmónico desde las nanocavidades encuentran una mejora coherente . Además, las distribuciones del campo eléctrico revelan que existe una antifase entre las nanocavidades y la guía de ondas del bus plasmónico a 2408 y 2457 nm, es decir, se han cumplido las condiciones de resonancia destructiva que resulta en la inhibición de las ondas de transmisión [12].
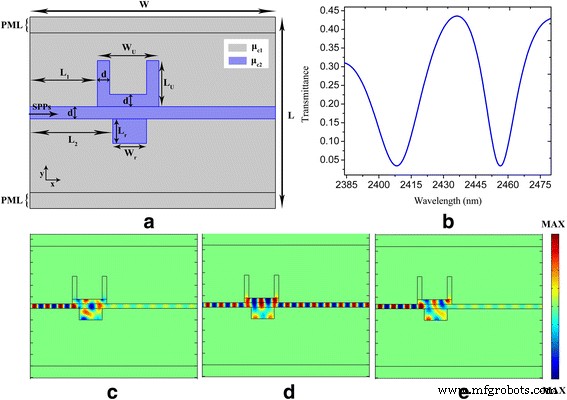
a, b La configuración esquemática y los parámetros geométricos del sistema de guía de ondas acoplado a nanocavidades rectangulares y en forma de U y la transmitancia espectral correspondiente, respectivamente. c - e Campo eléctrico ( E años ) distribución en longitudes de onda de 2408, 2437 y 2457 nm respectivamente. Los parámetros se establecen como W =800 nm, L =620 nm, d =20 millas náuticas, ancho U =150 nm, L U =120 nm, L 1 =220 nm, L 2 =250 nm, L r =50 millas náuticas, ancho r =100 nm, τ =1 ps, μ c1 =0,3 eV y μ c2 =0,9 eV
Calculamos la transmitancia espectral para el sistema de guía de ondas de bus plasmónico acoplado a nanocavidades rectangulares y en forma de U con tiempo de relajación variado τ =0,6, 0,8 y 1 ps, y los resultados se muestran en la figura 4a. Se puede ver que el contraste de transmisión aumenta con el aumento del tiempo de relajación. Además, la sintonización dinámica de la ventana PIT se muestra en la Fig. 4b. El potencial químico μ c1 se mantiene constantemente en 0,3 eV, mientras que μ c2 es 0,89, 0,895 y 0,9 eV. Como el potencial químico μ c2 aumenta, el pico de transmisión (en las longitudes de onda de 2452, 2445 y 2437 nm) en la ventana PIT está obviamente desplazado al azul. Como resultado, el efecto PIT dinámicamente sintonizable se realiza en nuestra nanoestructura propuesta modificando el potencial químico de las nanocavidades y la guía de onda del bus plasmónico.
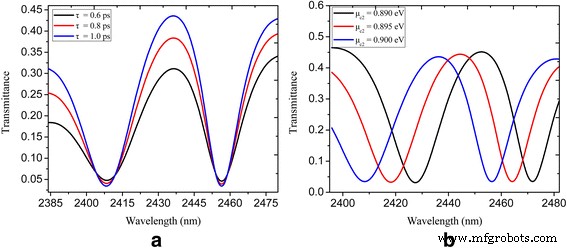
La transmitancia espectral del sistema de guía de ondas acoplado a nanocavidades rectangulares y en forma de U que se muestra en la Fig. 3: a con τ =0,6, 0,8 y 1 ps; b con μ c2 =0,89, 0,895 y 0,9 eV
Para investigar cómo los parámetros geométricos influyen en el fenómeno PIT, modificamos la ubicación de la nanocavidad rectangular. La Figura 5a muestra la transmitancia espectral del sistema de guía de ondas de bus plasmónico acoplado a nanocavidades rectangulares y en forma de U, donde se ve que el pico de transmisión aumentó (aumentó de 0.44 a 0.52) y la ventana PIT se amplía con L 2 aumentando para un cierto rango, que se atribuye a la intensificación de la fuerza de acoplamiento entre las dos nanocavidades [11, 28]. Además, encontramos que la disminución del ancho de la nanocavidad rectangular puede conducir a un pico de transmisión más alto (aumentado de 0.44 a 0.48) como se muestra en la Fig. 5b. Esto ofrece otra opción para ajustar la ventana PIT. El factor de calidad (factor Q) de las ventanas PIT se define como λ 0 / ∆ λ , donde λ 0 y ∆ λ son la longitud de onda máxima de transmisión y el ancho completo a la mitad del máximo (FWHM). En nuestra nanoestructura plasmónica propuesta, se obtiene una FWHM de menos de 30 nm y un factor Q de alrededor de 80, que es mucho más estrecho y más alto que las contrapartes del PIT basado en grafeno propuesto en las referencias mencionadas [28, 29].
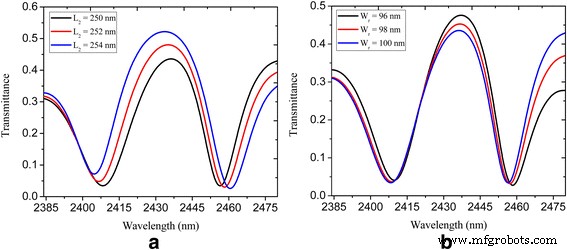
Transmitancia espectral del sistema de guía de ondas acoplado a nanocavidades rectangulares y en forma de U que se muestra en la Fig.3: a con L 2 =250, 252 y 254 nm; b con W r =96, 98 y 100 nm
De acuerdo con CMT, la transmitancia en nuestra nanoestructura plasmónica se expresa como [12, 42]
$$ T ={\ left | \ frac {j \ left ({\ omega} _ {\ mathrm {U}} - {\ omega} _ {\ mathrm {r}} \ right) + \ gamma +1} { j \ left ({\ omega} _ {\ mathrm {U}} - {\ omega} _ {\ mathrm {r}} \ right) + \ beta + \ gamma +1} \ right |} ^ 2 $$ ( 6)donde γ y β representan el coeficiente de acoplamiento entre las dos nanocavidades y el coeficiente de acoplamiento entre las nanocavidades y la guía de ondas del bus plasmónico, respectivamente. Podemos encontrar que la ventana PIT se puede obtener cuando las frecuencias de resonancia de la nanocavidad en forma de U ω U y la nanocavidad rectangular ω r son aproximadamente equivalentes. Y el pico de transmisión correspondiente es | ( γ + 1) / ( β + γ + 1) | 2 .
Con base en la estructura que se muestra en la Fig. 3a, construimos el sensor de índice de refracción, que se realiza modificando la permitividad relativa en la Ec. 1. La Figura 6a ilustra la transmitancia espectral con diferente índice de refracción n , que se refiere al índice de refracción del material de subdetección. Se puede ver que las longitudes de onda pico / dip1 / dip2 cambian de 2437.3 a 2457.3 nm / 2410.3 a 2432.4 nm / 2457.3 a 2474.9 nm cuando el índice de refracción n varía de 1 a 1,06. Como el índice de refracción n aumenta, tanto el pico como las caídas de la transmisión presentan un corrimiento al rojo. La sensibilidad de detección del sensor de índice de refracción, definida como el cambio en la longitud de onda pico / dip1 / dip2 por variaciones unitarias del índice de refracción dλ / dn es 333,3, 368,3 y 293,3 nm / RIU respectivamente. La Figura 6b muestra los picos y caídas de la transmitancia espectral con índice de refracción n variando de 1 a 1,19, donde podemos ver la relación aproximadamente lineal de las longitudes de onda pico / caída versus el índice de refracción n .
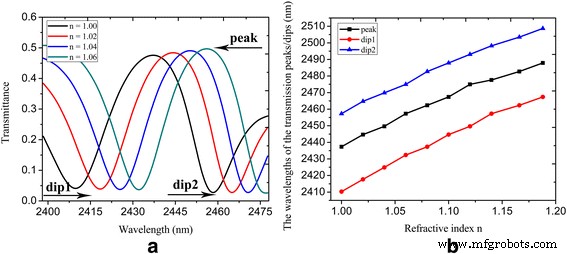
un La transmitancia espectral con índice de refracción n =1, 1.02, 1.04 y 1.06; b las longitudes de onda de pico / caída de la transmitancia espectral frente al índice de refracción n . Los parámetros se establecen como W =800 nm, L =620 nm, d =20 millas náuticas, ancho U =150 nm, L U =120 nm, L 1 =220 nm, L 2 =250 nm, L r =50 millas náuticas, ancho r =96 nm, τ =1 ps, μ c1 =0,3 eV y μ c2 =0,9 eV
Es bien sabido que el fenómeno PIT se acompaña del efecto de luz lento provocado por la fuerte dispersión [13, 29]. El efecto de luz lento se puede caracterizar por el retraso de grupo expresado como τ g = ∂φ ( ω ) / ∂ ω donde φ ( ω ) es el desplazamiento de fase efectivo del espectro de transmisión. En la Fig.7, trazamos los retrasos de grupo dentro de la ventana PIT a diferentes potenciales químicos μ c2 . En las proximidades del pico de transmisión PIT, ofrece grandes retrasos de grupo positivos que indican el efecto de luz lento. Las longitudes de onda máximas del sistema PIT en μ c2 =0,89, 0,895 y 0,9 eV son 2449,7, 2442,3 y 2434,7 nm, respectivamente, y los retardos de grupo correspondientes son 0,99, 1,1 y 1,02 ps, respectivamente. Por lo tanto, el efecto de luz lenta se ajusta de manera efectiva modificando el potencial químico de las nanocavidades y la guía de ondas del bus plasmónico. También se debe señalar que este es un artículo de prueba de concepto. En realidad, la estructura propuesta debería estar sobre el sustrato, donde el índice de refracción es mayor que el aire, y la respuesta de frecuencia cambiaría en consecuencia. Además, el confinamiento del plasmón es mayor, acompañado por el aumento de la pérdida, lo que resulta en la reducción del valor pico de la ventana de transparencia en el espectro de transmisión. Sin embargo, el principio es idéntico al caso suspendido.
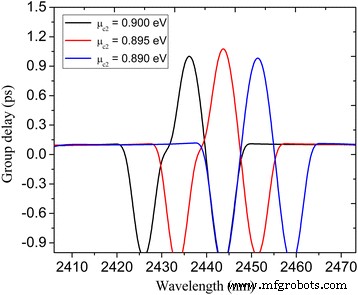
El grupo se retrasa frente al potencial químico μ c2 para el sistema de grafeno PIT que se muestra en la Fig. 3a. Los otros parámetros se establecen como W =800 nm, L =620 nm, d =20 millas náuticas, ancho U =150 nm, L U =120 nm, L 1 =220 nm, L 2 =254 nm, L r =50 millas náuticas, ancho r =96 nm, τ =1 ps, μ c1 =0,3 eV
Conclusiones
En conclusión, se han propuesto y modelado efectos PIT dinámicamente ajustables en nanoestructura plasmónica basada en grafeno compuesta por una guía de onda de bus plasmónico acoplada lateralmente a nanocavidades rectangulares y en forma de U utilizando el método de elementos finitos. La sintonización dinámica de las ventanas PIT se obtiene modificando el potencial químico de las nanocavidades y la guía de ondas del bus plasmónico. Además, la ventana PIT se puede ajustar dinámicamente mediante el ajuste de los parámetros geométricos de la nanoestructura, como la ubicación y el ancho de la nanocavidad rectangular. En comparación con los resonadores de anillo convencionales [24, 25], nuestros resonadores rectangulares y en forma de U asimétricos propuestos ofrecen una fuerza de acoplamiento más fuerte entre los resonadores y la guía de ondas del bus, lo que además da como resultado un efecto PIT más fuerte. Por otro lado, a diferencia de otras guías de ondas de nanocintas informadas, nuestras estructuras están formadas por la variación local del potencial químico en la monocapa de grafeno idéntica, y esto proporciona una integración más fácil con otros componentes funcionales en la misma plataforma de material. Además, esta nanoestructura plasmónica se puede utilizar como sensor de índice de refracción con alta sensibilidad de detección. Y el efecto de luz lento con un gran retraso de grupo también se realiza en el sistema PIT. La nanoestructura propuesta allana un nuevo camino hacia la realización de dispositivos nanofotónicos integrados en chip basados en grafeno.
Abreviaturas
- CMT:
-
Teoría del modo acoplado
- EIT:
-
Transparencia inducida electromagnéticamente
- FEM:
-
Método de elementos finitos
- PIT:
-
Transparencia inducida por plasmón
- RIU:
-
Unidad de índice de refracción
- SPP:
-
Polaritones de plasmón de superficie
Nanomateriales
- El grafeno pone los nanomateriales en su lugar
- Grafeno en altavoces y auriculares
- Nanocinta de grafeno
- Células solares de grafeno de alta eficiencia
- Control de no linealidad dual de las propiedades de modo y dispersión en la guía de ondas plasmónica de grafeno-dieléctrico
- La liberación sucesiva de inhibidores tisulares de metaloproteinasa-1 a través del sistema de administración a base de óxido de grafeno puede promover la regeneración de la piel
- Evaluación de estructuras de grafeno / WO3 y grafeno / ceO x como electrodos para aplicaciones de supercondensadores
- Preparación de polimerización in situ de nanocompuesto de polietileno / grafeno de peso molecular ultra alto mediante una estructura esférica y en sándwich Soporte de grafeno / Sio2
- Diseño de un absorbedor de terahercios de banda ultra ancha sintonizable basado en varias capas de cintas de grafeno
- Dispositivo basado en grafeno para biosensores ultrasensibles
- Sistema de seguimiento de movimiento 3D para tecnología autónoma



