home Tecnología de fabricación Equipo de fabricación
Manufactura industrial
Internet industrial de las cosas | Materiales industriales | Mantenimiento y reparación de equipos | Programación industrial |
home  MfgRobots >> Manufactura industrial >  >> Industrial materials >> Nanomateriales

Control de no linealidad dual de las propiedades de modo y dispersión en la guía de ondas plasmónica de grafeno-dieléctrico

Resumen

Estudiamos las propiedades de modo y dispersión de la guía de onda plasmónica no lineal dieléctrica-grafeno considerando la no linealidad dual del dieléctrico y el grafeno. Para la polarización TM, la distribución de modo, la distribución de permitividad y la relación de dispersión se obtuvieron resolviendo numéricamente las ecuaciones de Maxwell. En comparación con el caso que considera solo la no linealidad del dieléctrico, la intensidad del campo inicial para excitar los modos de plasmón se reduce obviamente al introducir la no linealidad dual. Además, se discute la influencia de la no linealidad dual en la relación de dispersión, y encontramos que la no linealidad del grafeno afecta fuertemente las propiedades de dispersión. La introducción de la no linealidad dual conduce a la disminución de la intensidad del campo inicial, que tiene una aplicación potencial en interruptores totalmente ópticos con umbral bajo.

Antecedentes

Los plasmónicos de grafeno han atraído una gran atención [1, 2, 3, 4] debido a las características ópticas y electrónicas únicas del grafeno en comparación con los metales. En THz y el rango de frecuencia del infrarrojo lejano, la transición de electrones dentro de la banda domina y el grafeno se comporta como un metal. Por lo tanto, los polaritones de plasmón de superficie (SPP) podrían estar respaldados por grafeno. Para la estructura compuesta de múltiples capas grafeno-dieléctrico, se han investigado los modos de excitación, acoplamiento y propagación de los SPP. El modo electromagnético cuasi-transversal se encontró en una guía de ondas de placas paralelas de grafeno [5]. El acoplamiento de SPP se estudió [6, 7] en una estructura multicapa grafeno-dieléctrico. Para la estructura de matriz periódica de láminas de grafeno monocapa, surge un fuerte acoplamiento entre los SPP cuando las láminas de grafeno se colocan firmemente.

Se han dedicado considerables esfuerzos a investigar las propiedades ópticas de las estructuras compuestas no lineales de grafeno-dieléctrico [8,9,10,11,12] por su gran potencial para controlar la propagación de la luz a micro y nanoescala. Para el caso del grafeno de capa única, se discutieron los plasmones superficiales en la interfaz entre el grafeno y el sustrato no lineal de tipo kerr [8]. Se muestra que la longitud de onda de los plasmones de grafeno se puede ajustar ajustando la permitividad no lineal de los sustratos. Para la estructura multicapa de grafeno-dieléctrico no lineal, se exploraron las propiedades de propagación y localización de los plasmones de grafeno, y se obtuvieron las relaciones de dispersión exactas para los plasmones de superficie de TM de una guía de ondas de placas paralelas de grafeno [11]. La propagación y la longitud de localización se ven notablemente afectadas por el ajuste de permitividades no lineales. Recientemente, la relación de dispersión para los modos plasmón simétrico y antisimétrico se ha derivado en una estructura de losa kerr recubierta de grafeno [12]. A excepción del modo típico de propagación hacia adelante, se encontraron los modos simétrico y antisimétrico.

Sobre la base de la fuerte no linealidad del grafeno, se han predicho varios efectos ópticos no lineales [13,14,15,16,17]. Nesterov y col. [15] estudiaron la propagación no lineal de la luz en una monocapa de grafeno y encontraron que la monocapa de grafeno puede soportar el solitón óptico espacial TE y TM en frecuencias ópticas debido a la no linealidad intrínseca del grafeno. Más recientemente, reemplazando el grafeno monocapa por grafeno multicapa, Smirnova et al. [16] investigó las propiedades no lineales de una pila multicapa de hojas de grafeno y derivó las ecuaciones no lineales que describen la dinámica espacial de los plasmones no lineales. Los estudios anteriores se centraron principalmente en la influencia de la no linealidad simple en el control de las propiedades de la luz en estructuras dieléctricas de grafeno. La idea del control dual de no linealidad se introdujo en las superredes fotónicas basadas en grafeno [18, 19], en las que se logró el control eléctrico y totalmente óptico de los haces fotónicos con precisión de sublongitud de onda profunda. Sin embargo, el control dual de no linealidad del modo y las propiedades de dispersión en la estructura plasmónica grafeno-dieléctrica todavía deja abiertas muchas preguntas. Por lo tanto, en este artículo consideramos la no linealidad del grafeno y el dieléctrico simultáneamente en la guía de ondas grafeno-dieléctrico-grafeno, y estudiamos la influencia de la no linealidad dual en las propiedades de dispersión y acoplamiento de modos.

Métodos

La guía de onda plasmónica dieléctrica no lineal de grafeno se ilustra esquemáticamente en la Fig.1, una placa paralela de grafeno con una conductividad σ g se coloca en x =± d / 2, donde el dieléctrico es un medio de tipo kerr con una permitividad ε = ε L + α | E | 2 . En nuestro análisis, el grafeno se trata como un límite debido a su grosor en una escala de átomo. Considerando un SPP magnético transversal (TM) que se propaga a lo largo de z dirección con una constante de propagación β y decae exponencialmente a lo largo de la x dirección hacia el aire y medio no lineal, respectivamente.

Diagrama esquemático de la guía de ondas plasmónica de grafeno-dieléctrico-grafeno no lineal

Para la polarización TM, sabemos que hay tres componentes de campo E x , E z y H y . El campo magnético H = H y años y campo eléctrico E = E x x + E z z satisfacer las ecuaciones

$$ \ frac {d {E} _z} {dx} =i \ omega {\ mu} _0 {H} _y + i \ beta {E} _x $$ (1) $$ i \ beta {H} _y =- i \ omega {\ varepsilon} _0 \ varepsilon {E} _x $$ (2) $$ \ frac {d {H} _y} {dx} =i \ omega {\ varepsilon} _0 \ varepsilon {E} _z $$ (3)

donde ε 0 y μ 0 son la permitividad eléctrica y la permeabilidad magnética del vacío. De la ecuación. (2) y ε = ε L + α | E | 2 podemos conseguir

$$ {\ varepsilon} ^ 2 {E} _x ^ 2 =\ frac {\ beta ^ 2} {\ omega ^ 2 {\ varepsilon} _0 ^ 2} {H} _y ^ 2 $$ (4) $$ { E} _x ^ 2 =\ left (\ varepsilon - {\ varepsilon} _L- \ alpha {E} _z ^ 2 \ right) / \ alpha $$ (5)

Sustituyendo la ecuación. (5) en la ecuación. (4) tenemos

$$ {\ varepsilon} ^ 3- \ left ({\ varepsilon} _L + \ alpha {E} _z ^ 2 \ right) {\ varepsilon} ^ 2- \ frac {\ alpha {\ beta} ^ 2} {\ omega ^ 2 {\ varepsilon} _0 ^ 2} {H} _y ^ 2 =0 $$ (6)

Para la ecuación cúbica [20, 21]

$$ {x} ^ 3 + b {x} ^ 2 + c x + d =0 $$ (7)

El discriminante de la ecuación. (7) es

$$ \ varDelta ={b} ^ 2 {c} ^ 2-4 {c} ^ 3-4 {b} ^ 3 d + 18 b c d-27 {d} ^ 2 $$ (8)

Configuración de \ (b =- \ left ({\ varepsilon} _L + \ alpha {E} _z ^ 2 \ right), \ kern0.5em c =0 \) y \ (d =- \ alpha {\ beta} ^ 2 {H} _y ^ 2 / \ left ({\ omega} ^ 2 {\ varepsilon} _0 ^ 2 \ right) \), es fácil demostrar que el discriminante de la Ec. (6) cumple

$$ \ varDelta =- {\ left ({\ varepsilon} _L + \ alpha {E} _z ^ 2 \ right)} ^ 3 \ frac {\ alpha {\ beta} ^ 2} {\ omega ^ 2 {\ varepsilon} _0 ^ 2} {H} _y ^ 2-27 \ frac {\ alpha ^ 2 {\ beta} ^ 4} {\ omega ^ 4 {\ varepsilon} _0 ^ 4} {H} _y ^ 4 <0 $$ ( 9)

Δ <0 significa que la Eq. (6) solo tiene una solución real. Por el método de Cardano [20], sabemos que para la ecuación cúbica Eq. (7) su raíz real es

$$ x =- \ frac {b} {3} + \ sqrt [3] {- \ frac {q} {2} + \ sqrt {{\ left (\ frac {p} {3} \ right)} ^ 3 + {\ left (\ frac {q} {2} \ right)} ^ 2}} + \ sqrt [3] {- \ frac {q} {2} - \ sqrt {{\ left (\ frac {p } {3} \ right)} ^ 3 + {\ left (\ frac {q} {2} \ right)} ^ 2}} $$ (10)

donde p = c - b 2 / 3, q = d - bc / 3 + 2 b 3 / 27. Usando la ecuación. (10) podemos obtener el ε . Reemplazo de ε en Eq. (2) y (3) mediante la solución real, las ecuaciones diferenciales ordinarias se pueden resolver numéricamente mediante un método de relajación.

Resultados y discusiones

De los requisitos de continuidad de E z y H y , las condiciones de contorno en x =± d / 2 satisfacen E 1 z = E 2 z y H 2 años - H 1 año = σ g E z . La conductividad superficial del grafeno σ g se rige por la fórmula de Kubo [22] que incluye las contribuciones de transición entre bandas e intrabandas. En el rango de frecuencia de THz e infrarrojo lejano, la contribución de transición intrabanda domina y la conductividad de la superficie se puede simplificar a un tipo Drude simple como [23]

$$ {\ sigma} _g =\ frac {e ^ 2 {\ mu} _c} {\ pi {\ hslash} ^ 2} \ frac {\ mathrm {i}} {\ omega + \ mathrm {i} {\ tau} ^ {- 1}} $$ (11)

donde e es la carga del electrón, μ c es el potencial químico del grafeno, ω es la frecuencia y τ es el momento de relajación del impulso. Este modelo es aplicable en el límite de temperatura baja ( k B T << μ c ) a baja frecuencia ( ℏω ≤ μ c ). Para la condición de campo fuerte, se debe considerar la parte no lineal de la conductividad y se lee la conductividad total del grafeno [16]

$$ {\ sigma} _g ={\ sigma} _L + {\ sigma} ^ {NL} {\ left | {E} _ {\ tau} \ right |} ^ 2 $$ (12)

donde E τ es la componente tangencial del campo eléctrico y σ NL denota conductividad no lineal [16]

$$ {\ sigma} ^ {NL} =- i \ frac {3} {8} \ frac {e ^ 2} {\ pi {\ hslash} ^ 2} {\ left (\ frac {e {\ nu} _F} {\ mu_c \ omega} \ right)} ^ 2 \ frac {\ mu_c} {\ omega} $$ (13)

donde ν F =0,95 × 10 8 cm / s es la velocidad de Fermi.

Para el grafeno, solo en THz y en el rango de frecuencia del infrarrojo lejano se puede simplificar su conductividad superficial a un tipo Drude simple; por lo tanto, elegimos la longitud de onda incidente como λ =10 μm . Otros parámetros se fijan a los valores ε 1 =1, ε L =2.25, α =5 × 10 - 16 (m / v) 2 [24] E F =0,27 ev, τ =1,5 ps. Es bien sabido que hay dos modos en las estructuras lineales grafeno-dieléctrico-grafeno, que son modos simétricos y antisimétricos, respectivamente. A continuación, discutiremos la influencia de la no linealidad en la distribución de modos en las estructuras compuestas de grafeno-dieléctrico.

Configuración de H 0 como componente del campo magnético inicial en la interfaz incidente, al resolver las ecuaciones (1, 2 y 3) numéricamente, la dependencia de la intensidad del campo magnético inicial H 0 en la constante de propagación β se da en la Fig. 2. La constante de propagación normalizada \ ({k} _F =\ sqrt {\ uppi n} \) está en unidades de momento de Fermi [25], donde n =6 × 10 12 cm - 2 es la densidad de portadores. Las curvas sólidas representan el caso de que solo se considera la no linealidad del dieléctrico, mientras que las curvas discontinuas indican el caso de que la no linealidad del dieléctrico y el grafeno se consideran simultáneamente. De la Fig. 2 encontramos que las propiedades de los modos para ambos casos son las mismas. Hay tres ramas, lo que significa que la guía de onda plasmónica no lineal puede admitir tres modos. Sin embargo, en comparación con el caso de no linealidad simple, la intensidad del campo inicial se redujo aparentemente para el caso de no linealidad dual. Aunque la guía de ondas plasmónica no lineal de grafeno puede admitir tres modos, es imposible distinguir qué rama denota un modo simétrico, antisimétrico o asimétrico. Para determinar las propiedades modales de cada rama, trazamos el campo eléctrico y la distribución del campo magnético asociados con A, B, C y D en la Fig. 3, respectivamente.

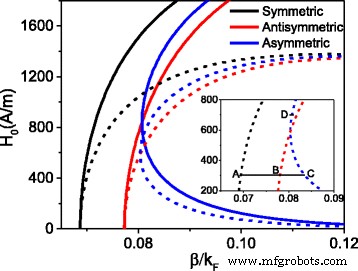
La intensidad magnética inicial frente a la constante de propagación. Para las curvas sólidas : α =5 × 10 - 16 ( m / v ) 2 , σ NL =0; para las curvas discontinuas : α =5 × 10 - 16 ( m / v ) 2 , σ NL =2,19 × 10 - 20 i, la línea sólida negra horizontal es una línea auxiliar

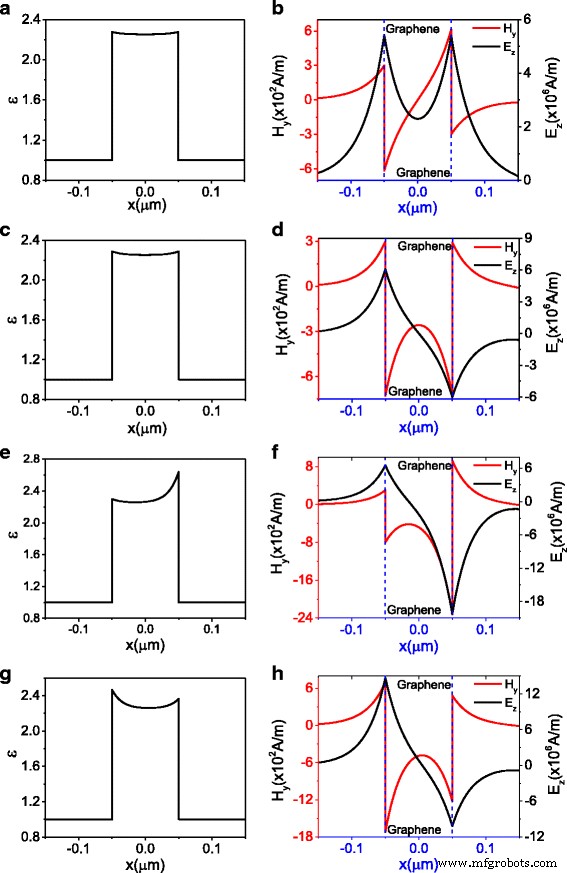
La permitividad y la distribución de modos para el componente magnético H y y componente eléctrico E z . un y b corresponden al punto A ( H 0 =300, β =6,94 × 10 - 2 k F ) marcado en la Fig.2 para modos simétricos, c y d corresponden al punto B ( H 0 =300, β =7,81 × 10 - 2 k F ) marcado en la Fig.2 para modos antisimétricos, e y f corresponden al punto C ( H 0 =300, β =8,36 × 10 - 2 k F ) marcado en la Fig.2 para modos asimétricos, y g y h corresponden al punto D ( H 0 =700, β =8.07 × 10 - 2 k F )

Para la rama de la curva de trazos negros, la permitividad correspondiente y los campos asociados con A se representan en la Fig. 3a, b, en la que la distribución de la permitividad y el campo eléctrico E z es simétrico. Por lo tanto, esta rama representa el modo simétrico. Para la rama de la curva de trazos rojos, la permitividad y los campos asociados con B se dan en la Fig. 3c, d. La distribución de la permitividad sigue siendo simétrica; sin embargo, la distribución del campo eléctrico E z es antisimétrico, lo que implica que esta rama es un modo antisimétrico. La distribución de la permitividad y el campo asociados con C y D se grafican en la Fig. 3e – h. Se observa que la distribución del campo magnético y el campo eléctrico correspondientes asociados con C y D es asimétrica; por lo tanto, la rama de la curva de trazos azules representa el modo asimétrico. Mientras tanto, la distribución asimétrica del campo eléctrico conduce a la distribución asimétrica de la permitividad.

A continuación, dirigimos nuestra atención a discutir la influencia de la no linealidad del dieléctrico y el grafeno en la relación de dispersión. La Figura 4 muestra la relación de dispersión para un campo magnético inicial fijo ( H 0 =300 A / m) y diferentes potenciales químicos y coeficientes dieléctricos no lineales. En la Fig. 4a-c, se muestra la influencia del coeficiente no lineal del dieléctrico sobre la relación de dispersión, donde solo se considera la no linealidad del dieléctrico. Cuando tanto el coeficiente no lineal como la conductividad no lineal son iguales a cero ( α =0, σ NL =0), la estructura no lineal degenera en una estructura lineal. En la Fig. 4a, para el caso lineal, solo existen modos simétricos y antisimétricos. La curva sólida negra y la curva sólida roja representan los modos simétrico y antisimétrico, respectivamente. Cuando el coeficiente no lineal es distinto de cero, aparece un modo asimétrico como la rama III que se muestra en la Fig. 4b, c en la estructura. A medida que el coeficiente no lineal aumenta aún más, la influencia del coeficiente en las propiedades de dispersión se vuelve débil.

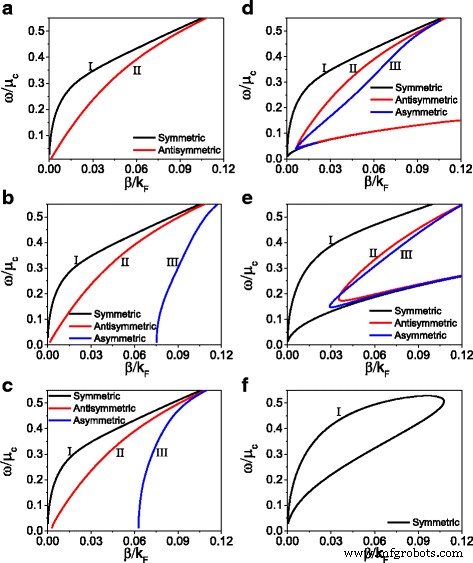
La relación de dispersión para una intensidad magnética inicial fija ( H 0 =300 A / m) y para varios coeficientes no lineales ( a - c ) y para diversos potenciales químicos ( d - f ). un α =0, μ c =0.27eV, σ NL =0, b α =5 × 10 - 17 (m / V) 2 , μ c =0.27eV, σ NL =0, c α =5 × 10 - 16 (m / V) 2 , μ c =0.27eV, σ NL =0, d μ c =0.27eV, α =5 × 10 - 16 (m / V) 2 , ( e ) μ c =0,16eV, α =5 × 10 - 16 (m / V) 2 y f μ c =0.10eV, α =5 × 10 - 16 (m / V) 2

A continuación, presentamos simultáneamente la no linealidad del dieléctrico y el grafeno, y discutimos la influencia de la no linealidad del grafeno en la relación de dispersión con un coeficiente no lineal fijo de dieléctrico α =5 × 10 - 16 (m / V) 2 . Los resultados se muestran en la Fig. 4d-f. Comparada la Fig. 4d con la Fig. 4c, se observa que el fenómeno de repliegue de la relación de dispersión aparece en las tres ramas. De la ecuación. (13), sabemos que la no linealidad del grafeno se puede controlar ajustando el potencial químico. A medida que la no linealidad del grafeno aumenta aún más de μ c =0,27 eV a μ c =0.16 eV, como se muestra en la Fig. 4e, el punto de repliegue de la relación de dispersión se mueve hacia arriba. Para una mayor no linealidad del grafeno (con un pequeño potencial químico μ c =0.10eV), como se muestra en la Fig. 4f, solo el modo simétrico aparece y forma un bucle cerrado. De la Fig. 4, sabemos que considerando solo la no linealidad del dieléctrico, la relación de dispersión muestra tres ramas que son casi inalterables a medida que aumenta el coeficiente no lineal del dieléctrico. Sin embargo, cuando introducimos aún más la no linealidad del grafeno, aparece el fenómeno de repliegue de la relación de dispersión. Para el campo magnético inicial especificado H 0 y potencial químico la relación de dispersión solo muestra un modo simétrico con un circuito cerrado.

Conclusiones

En resumen, hemos investigado el modo y las propiedades de dispersión de la guía de onda plasmónica no lineal dieléctrica de grafeno. La distribución de modos, la permitividad y las relaciones de dispersión se obtuvieron resolviendo numéricamente la ecuación de Maxwell para la polarización de TM. En comparación con el caso que considera solo la no linealidad del dieléctrico, la intensidad del campo inicial se redujo aparentemente al considerar la no linealidad del dieléctrico y el grafeno simultáneamente. Además, la no linealidad dual afecta significativamente las propiedades de dispersión de la guía de ondas. Especialmente, a medida que aumenta la no linealidad del grafeno, los modos antisimétrico y asimétrico se fusionan en uno y desaparecen gradualmente. Por lo tanto, solo se puede encontrar el modo simétrico en el caso de una fuerte no linealidad.


Nanomateriales

  • Metal
  • Resina
  • fibra
  • Material compuesto
  • Nanomateriales
  • Materiales poliméricos
  • Biologicos
  • Teñir
  • Especias

    1. Grafeno en altavoces y auriculares
    2. Preparación y propiedades magnéticas de nanopartículas de espinela de FeMn2O4 dopadas con cobalto
    3. Hacia los nanofluidos de TiO2:Parte 1:Preparación y propiedades
    4. Compuestos de grafeno y polímeros para aplicaciones de supercapacitores:una revisión
    5. Propiedades infrarrojas y modulación de onda de terahercios de grafeno / ferrita MnZn / heterouniones p-Si
    6. Bioseguridad y capacidad antibacteriana del grafeno y el óxido de grafeno in vitro e in vivo
    7. Efecto sinérgico del grafeno y los MWCNT en la microestructura y las propiedades mecánicas de los nanocompuestos de Cu / Ti3SiC2 / C
    8. Evaluación de estructuras de grafeno / WO3 y grafeno / ceO x como electrodos para aplicaciones de supercondensadores
    9. Prueba de las propiedades estructurales, electrónicas y magnéticas de Ag n V (n =1–12) Clusters
    10. Síntesis sonoquímica de un solo paso y propiedades fotocatalíticas fáciles de compuestos de puntos cuánticos de grafeno / Ag3PO4
    11. Dependencia de la toxicidad de las nanopartículas en sus propiedades físicas y químicas