Placa de cuarto de onda de transmisión ultrafina de banda ancha con matriz de orificios rectangulares basada en resonancias plasmónicas
Resumen
El control de los estados de polarización de la luz juega un papel importante en los sistemas ópticos modernos. Sin embargo, los dispositivos tradicionales de manipulación de polarización a menudo tienen un ancho de banda estrecho y su gran tamaño les dificulta lograr la miniaturización e integración de los sistemas ópticos. Este trabajo presenta una placa de cuarto de onda ultrafina con una matriz periódica de orificios rectangulares de película de plata de 2 × 2 con un espesor inferior a λ / 50. La simulación numérica muestra que la placa de ondas puede transformar eficientemente una onda polarizada circular en una polarizada linealmente en el centro de 1550 nm, y su ancho de banda es de 525 nm. Además, la placa de cuarto de onda puede invertir eficientemente la polarización lineal en polarización circular a 1550 nm, cuya elipticidad está cerca de la unidad. Con una serie de pequeños orificios en una película de metal para mejorar la transmisión, esta estructura puede aumentar la transmisión a 0,44. La placa de cuarto de onda de banda ancha se puede utilizar en un sistema de comunicación y en un sistema de banda de infrarrojo cercano, y se puede integrar con otros dispositivos ópticos a nanoescala para lograr la operación, detección y detección de polarización.
Introducción
Existe un interés creciente en manipular la polarización de la luz en una variedad de aplicaciones ópticas, como polarizadores, placas de ondas y lentes. Entre estos, las placas de ondas son componentes fotónicos importantes porque pueden introducir una diferencia de fase específica, como π / 2 y π, para producir luz polarizada diferente para lograr un cuarto o media placa de onda. El diseño tradicional de placa de onda utiliza la birrefringencia de cristales para imponer diferentes fases a la luz incidente. Sin embargo, el efecto de birrefringencia es muy débil en los cristales naturales, lo que da como resultado placas de ondas que tienen un espesor de varios cientos de micrones. Los componentes ópticos voluminosos a menudo adolecen de dificultades en la integración y la profundidad de modulación de fase [1, 2, 3, 4]. En los últimos años, la aparición de la nanofotónica ha abierto una nueva dirección para estudiar la interacción entre la luz y la materia. Especialmente, los dispositivos nanofotónicos (de aproximadamente decenas de nanómetros de espesor) pueden romper el límite de difracción sin interferencia electromagnética. Tiene un gran potencial para reemplazar los dispositivos de gran escala. Entre ellos, los dispositivos nanofotónicos basados en metasuperficie han atraído cada vez más la atención. El desarrollo de la teoría de la metasuperficie y la tecnología de fabricación permite desarrollar nanodispositivos [5].
Las metauperficies son estructuras planas que modifican localmente la polarización, la fase y la amplitud de la luz en reflexión o transmisión, lo que permite componentes ópticos planos con patrones litográficos con funcionalidades controladas por diseño. Suele tener un grosor menor que la longitud de onda. En el proceso de transmisión o reflexión, las metasuperficies anisotrópicas producen diferentes fases y amplitudes correspondientes a las ondas TE y TM, lo que proporciona una gran flexibilidad para el diseño de metasuperficies funcionales. Podemos usar esto para diseñar lentes, placas de fase, placas de ondas, polarizadores, divisores de haz, generadores de haces vectoriales arbitrarios, etc. [6,7,8,9,10,11,12,13,14,15, 16, 17].
Las placas de cuarto de onda de la metauperficie basadas en resonancias de plasmón son uno de los puntos calientes en los últimos años [18,19,20,21,22,23,24], y la bibliografía publicada en la línea de tiempo indica un progreso continuo en esta área. En 2011, Zhao et al. diseñó y estudió el rendimiento de una matriz de nanobarras de plata alargada ortogonal como una placa de cuarto de onda de banda ancha. Puede introducir un desplazamiento de fase de 90 ° sobre un espesor de 60 nm [25]. Inspirado por el principio de Babinet, en 2013, el mismo grupo diseñó una placa de un cuarto de onda de nano rendijas y logró la conversión de polarización circular a lineal (CTL) en la región de la luz visible. El espesor de la capa de metal se reduce a 40 nm [26]. Los dos diseños anteriores tienen una banda ancha de polarización CTL. Sin embargo, es difícil conseguir la misma amplitud de dos haces polarizados ortogonalmente. Poco después del trabajo pionero de Zhao et al., En 2012, Roberts et al. propuso una placa de cuarto de onda con una serie periódica de aberturas en forma de cruz en una película de plata. La eficiencia de transmisión y la fase (para ancho de brazo fijo) de la placa de ondas son sensibles a la longitud del brazo relacionado. La conversión de polarización lineal a circular (LTC) se logra en algunas longitudes de onda discretas de 710 a 760 nm, y el espesor de la película de plata es de 140 nm [27]. Puede lograr la polarización LTC, pero la longitud de onda se fija solo en longitudes de onda específicas y la capa de metal es relativamente gruesa. De manera similar, con base en la anisotropía causada por la longitud del brazo en las direcciones ortogonales, en 2013, Yang et al. propuso una placa de cuarto de onda que consiste en una matriz plana periódica de antenas de plasma simétricas en forma de L. La elipticidad de la luz transmitida puede alcanzar 0,994 a 1550 nm. El ancho de banda con elipticidad superior a 0,9 es 80 nm [28]. La polarizabilidad circular de la placa de ondas casi unitaria, aunque su ancho de banda, no es ideal. Al diseñar cuidadosamente las nanoantenas en los superuints, en 2015, Li et al. logró una placa de un cuarto de onda que consta de una matriz de nanovarillas de oro de 20 nm de espesor. Teóricamente puede realizar la conversión de la polarización CTL y la transformación inversa alrededor de 1550 nm. La polarizabilidad circular es 0,67 y la eficiencia de transmisión es 0,4 [29]. La estructura ultrafina puede realizar la polarización CTL en una banda ancha, pero la elipticidad (relación de amplitud) de la polarización LTC a 1550 nm es baja. Además, en 2017, Zhu et al. propuso una placa de onda de cuarto de onda de matriz de anillo rectangular roto. Está formado por dos pares de rendijas con orientación perpendicular incrustadas en una película de plata de 10 nm de espesor. Tiene un ancho de banda de polarización CTL de 120 nm. Además, la placa de ondas puede lograr la transformación LTC con una polarización circular de 0,97 y la eficiencia de transmisión es de 0,4 a 1550 nm [30]. Logra una alta conversión de polarización a expensas del ancho de banda.
A través de los ejemplos anteriores, generalmente, como una placa de cuarto de onda de transmisión miniaturizada ideal utilizada en la banda de comunicación, debe tener las siguientes características:en primer lugar, puede realizar la conversión de la polarización CTL (polarización LTC) en banda ancha. En segundo lugar, puede lograr la polarización circular cerca de la unidad a 1550 nm. En tercer lugar, la transmitancia general debe ser lo más alta posible (la transmitancia máxima de una placa de cuarto de onda ultrafina sin pérdida debe ser 0,5 calculada por la teoría de admitancia de superficie). En cuarto lugar, debe ser ultradelgado y rentable. Pero por ahora, la mayoría de ellos siguen siendo de diseño teórico y se han realizado pocos experimentos. Debido a que la relación entre la altura y el ancho es demasiado alta, o los parámetros estructurales son demasiado sensibles a los errores, etc., afectará el rendimiento de las placas de cuarto de onda reales.
Con base en las cuatro características anteriores, proponemos una placa de cuarto de onda de transmisión utilizada en la banda de comunicación. La celda unitaria está compuesta por una película de plata perforada de 27 nm de espesor y un sustrato de sílice. El diseño de cuatro orificios evita la desventaja del ancho de banda estrecho de un solo resonador. Pueden mejorar los plasmones superficiales localizados, aumentando así la anisotropía de fase para introducir cambios de fase abruptos y reduciendo en gran medida el grosor de la capa de metal. Además, la placa de ondas puede lograr una diferencia de fase de 90 ° en un ancho de banda de 525 nm. Especialmente, la polarización circular está cerca de la unidad con una eficiencia de transmisión de 0.44 a 1550 nm.
Métodos
La Figura 1 muestra esquemáticamente una celda unitaria de la placa plasmónica de cuarto de onda propuesta, una película de plata para excavar agujeros colocada sobre un sustrato de sílice. Se disponen cuatro aberturas rectangulares en dos filas y dos columnas. La placa de ondas sumergida en un ambiente de aire con índice de refracción n =1. Se supone que la sílice no es dispersiva (\ ({\ varepsilon} _ {SiO_2} =1.47 \)), y la permitividad de la plata se describe en el modelo de Drude [25]:
$$ {\ varepsilon} _ {Ag} ={\ varepsilon} _0 \ left [{\ varepsilon} _ {\ infty} - \ frac {f_p ^ 2} {f \ left (f- i \ gamma \ right)} \ right] $$ (1)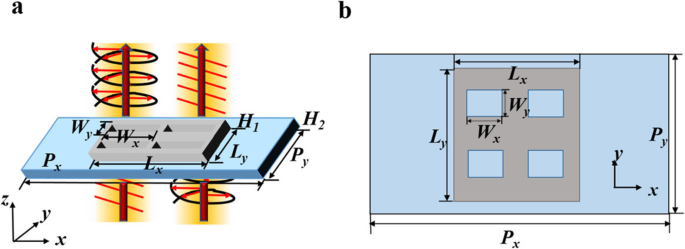
Esquemas de la placa de cuarto de onda. Las luces normalmente inciden desde abajo. un Vista 3D de la placa de cuarto de onda. b Vista superior de la estructura de una unidad
donde ε ∞ =5, f p =2,175 PHz y γ =4,35 THz. El espesor del sustrato de sílice y la película de plata se fija en H 1 =30 nm y H 2 =27 nm, el período de la unidad es P x =1200 nm y P y =500 nm, la longitud y el ancho de la película plateada son L x =450 nm y L y =480 nm, respectivamente. Las dimensiones internas de las aberturas W y =80 nm se mantiene fija y la longitud W x es variable. El centro de las aberturas son x =± 75 nm, años =± 110 nm. La simulación numérica se realiza mediante métodos tridimensionales en el dominio del tiempo de diferencias finitas (FDTD), en los que las condiciones periódicas se aplican en la x- y y- direcciones, y las capas que coinciden perfectamente se utilizan a lo largo de z- Dirección para asegurarse de que la absorción completa de la luz de excitación sin reflexión. Las ondas planas normalmente inciden desde la parte inferior del sustrato dentro de la región de longitud de onda de 1000 a 2000 nm. T es la transmitancia total normalizada y la transmitancia en x- y y -directions es T x y T y , respectivamente. Primero consideramos las características de transmisión de una metasuperficie plana ultradelgada con un espesor de sublongitud de onda d ≪ λ 0 colocado en el plano z =0. La transmisión se puede expresar simplemente usando la matriz de Jones:
$$ \ boldsymbol {T} =\ left (\ begin {array} {cc} {T} _ {xx} &{T} _ {xy} \\ {} {T} _ {yx} &{T} _ {yy} \ end {matriz} \ right) $$ (2)donde T ij representa la amplitud compleja de la onda transmitida, polarizada linealmente en el i dirección de excitación en el j dirección. Por lo tanto, T xx y T yy son los coeficientes de transmisión de copolarización y la T xy y T yx son los coeficientes de transmisión de polarización cruzada. Considere que la onda plana entrante se propaga a lo largo de + z -dirección, el campo eléctrico se puede expresar como:
$$ {\ boldsymbol {E}} _ {in} \ left (\ boldsymbol {r}, t \ right) =\ left (\ begin {array} {c} {I} _x \\ {} {I} _y \ end {matriz} \ right) {e} ^ {i \ left (kz- \ omega t \ right)} $$ (3)donde ω representa la frecuencia, k es el vector de onda y I x , yo y son las amplitudes complejas. La matriz I =\ (\ left (\ begin {array} {c} {I} _x \\ {} {I} _y \ end {array} \ right) \) determina el estado de polarización y la intensidad total de la onda. Cuando la luz linealmente polarizada incide normalmente en un ángulo de polarización de 45 ° con respecto a x- eje, ∣ I x ∣ =| yo años ∣ =\ (\ frac {1} {\ sqrt {2}} \). El campo eléctrico transmitido se puede describir como:
$$ {\ boldsymbol {E}} _ t \ left (\ boldsymbol {r}, t \ right) =\ left (\ begin {array} {c} {T} _x \\ {} {T} _y \ end { matriz} \ right) {e} ^ {i \ left (kz- \ omega t \ right)} $$ (4)Los campos de incidencia y transmisión están correlacionados por la matriz de Jones: E t =T E en , eso es
$$ \ left (\ begin {array} {c} {T} _x \\ {} {T} _y \ end {array} \ right) =\ left (\ begin {array} {cc} {T} _ { xx} &{T} _ {xy} \\ {} {T} _ {yx} &{T} _ {yy} \ end {array} \ right) \ left (\ begin {array} {c} {I } _x \\ {} {I} _y \ end {matriz} \ derecha) $$ (5)Para un medio que no tiene un efecto de conversión de polarización lineal ( T xy y T yx igual a cero [25, 27]), el campo transmitido se puede expresar como [16]:
$$ \ left (\ begin {array} {c} {T} _x \\ {} {T} _y \ end {array} \ right) =\ left (\ begin {array} {c} {T} _ { xx} {I} _x \\ {} {T} _ {yy} {I} _y \ end {matriz} \ derecha) $$ (6)La diferencia de fase es △ φ =φ y - φ x entre los coeficientes de transmisión T xx y T yy . Para una placa de cuarto de onda, el △ φ debe ser igual a (2 m + 1) π / 2 , donde m es un número entero.
Resultados y discusiones
Cambios de fase simulados φ x , φ y y sus diferencias se muestran en la Fig. 2a. El △ φ cae bruscamente a 1200 nm y finalmente se estabiliza alrededor de △ φ =90 °. Las curvas de transmitancia y la diferencia de fase cerca de 1550 nm se muestran en la Fig. 2b. Generalmente, se puede considerar que una placa de cuarto de onda con una diferencia de fase de 90 ° ± 5 ° funciona normalmente. Para 1328 nm, el △ φ =95 °, y para 1853 nm, △ φ =85 °, eso significa que dentro del ancho de banda del infrarrojo cercano de 525 nm, nuestro diseño puede realizar la conversión de polarización circular a polarización lineal. Esto es excelente en el ancho de banda publicado actualmente de la placa de cuarto de onda del infrarrojo cercano.
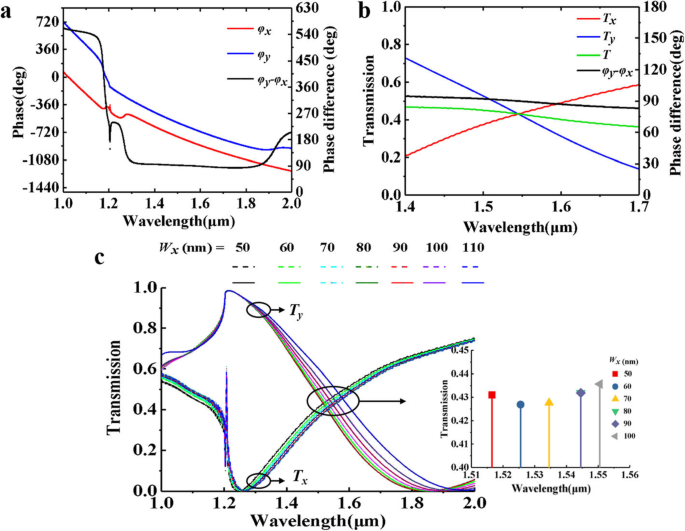
Resultados de la simulación de la estructura propuesta. un La fase de T x , T y y hay diferencia cuando W x =100 nm. b Transmitancia T , T x y T y y la diferencia de fase de las dos luces de transmisión. c T x y T y curvas cuando W x cambios. La imagen pequeña es el diagrama detallado cerca de 1550 nm. Muestra las tendencias de variación de T x , T y , transmitancia total T y diferencia de fase en la longitud de onda de comunicación
El tamaño cambiado W x del agujero tiene diferentes efectos en x- y y- polarización. La Figura 2c muestra la transmitancia cuando W x cambios. El pico de T y y el pico muy agudo de T x a 1200 nm están relacionados con la P x =1200 nm. La condición para que ocurran las anomalías de Wood es λ =p ( pecado θ i + 1) [31, 32] y θ i es 0 para onda incidente normalmente; por lo tanto, el pico ocurre cuando λ =P x . Además, con la disminución de P y , el valle de T x cambia a la dirección de la longitud de onda corta, y T y se mueve hacia la dirección de longitud de onda larga, lo que resulta en el cambio de longitud de onda y transmitancia correspondiente a la intersección de las dos curvas. Además, la pequeña imagen muestra las intersecciones de T x y T y cuando W x cambia de 50 a 100 nm. Significa la elipticidad | T y | / | T x | =1, de modo que la estructura propuesta pueda realizar la conversión de un cuarto de placa de onda de la polarización LTC. La eficiencia es de aproximadamente 0,44, que se acerca a la transmitancia ideal de 0,5 demostrada por el método de admitancia superficial en la literatura anterior [28]. Además, cuando el ancho de apertura W x aumenta de 50 a 100 nm, la longitud de onda operativa se cambia de 1518 (transmitancia de aproximadamente 0,43) a 1550 nm (transmitancia de aproximadamente 0,44). Esto significa que el trabajo propuesto tiene una buena solidez y es beneficioso para la preparación experimental.
Analizamos numéricamente las resonancias de dipolos eléctricos y magnéticos (ED y MD) bajo x-pol. y y-pol. en diferentes W x . Puede verse en la Fig. 3a, b que apenas hay resonancia MD en dos direcciones de polarización y existe resonancia ED a 1550 nm para x- polarización y 1600 nm para y- polarización. La Figura 3c muestra la intensidad y la dirección del campo eléctrico bajo x-pol. incidencia (λ =1550 nm) y Fig. 3d para y-pol. (λ =1600 nm). Las resonancias de ED se pueden ver desde la dirección indicada por las flechas vectoriales. El cambio de W x tiene poco efecto sobre la resonancia dipolo de x-pol. , pero y-pol. está relativamente afectado. Al cambiar el rango de la anomalía de Wood y la posición del dipolo eléctrico, la transmisión, la fase y la polarización de nuestro diseño pueden controlarse mejor. Esto nos permite obtener un mejor rendimiento de la placa de cuarto de onda en la banda del infrarrojo cercano. También proporciona una nueva idea para el diseño de placas de ondas de metasuperficie [33,34,35,36,37,38,39,40,41].
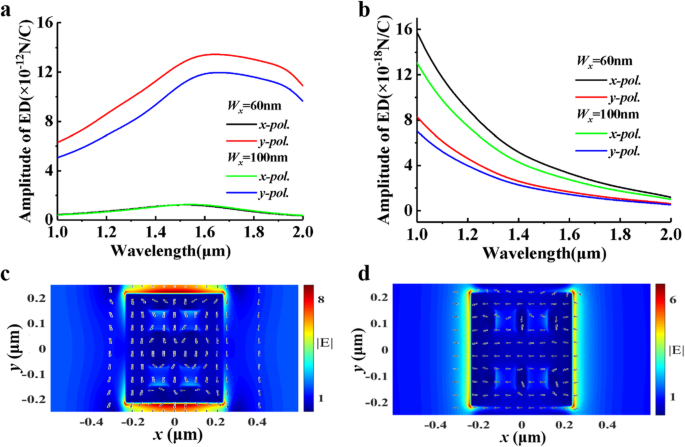
un La intensidad de las resonancias de la disfunción eréctil. b La intensidad de las resonancias MD. c, d La intensidad del campo eléctrico y los vectores de x-pol. y y-pol. incidencia, respectivamente
Para examinar la banda operativa de las placas de cuarto de onda y el rendimiento a la longitud de onda de comunicación alrededor de 1550 nm, dividimos las comparaciones en cuatro partes (que se muestran en la Tabla 1):polarizabilidad circular a 1550 nm, eficiencia de transmisión a 1550 nm, el espesor y se puede lograr el ancho de banda desde la polarización circular hasta la polarización lineal.
La primera columna de la Tabla 1 es la vista superior (bidimensional) de las estructuras, que es solo un diagrama esquemático y no muestra el tamaño y la proporción específicos. Los materiales se muestran simplemente en las figuras. La segunda columna es el ancho de banda de la estructura como placas de cuarto de onda, en la que la polarización circular se puede convertir en polarización lineal, y el rango de diferencia de fase es 90 ° ± 5 °. La tercera columna es la elipticidad de la transmisión de polarización LTC a 1550 nm y la elipicidad | T y | / | T x |. La cuarta columna es la longitud de onda correspondiente cuando la elipticidad | T y | / | T x | =1, y el △ φ =φ y -φ x =(2 m + 1) × 90 ° simultáneamente, donde m es un entero. La quinta columna es el grosor de la capa de metal de cada cuarto de placa de onda y la sílice es el único otro material. Los resultados de todos los artículos anteriores provienen de simulaciones, utilizando FEM, FDTD, etc.
El rendimiento de cinco estructuras que trabajan con ancho de banda de comunicación en la Tabla 1a, d, e, fyg se presenta como gráficos de barras. Representan las nanovarillas, las matrices de anillos rectangulares rotos en forma de L, la matriz de nanobarras de oro de una sola capa y las estructuras de película de plata con orificios rectangulares de dos por dos, respectivamente. La polarización circular y la eficiencia de transmisión de diferentes placas de cuarto de onda a 1550 nm se muestran en la Fig. 4a, y su respectivo espesor de capa metálica y ancho de banda de trabajo se muestran en la Fig. 4b. Por conveniencia, normalizamos el grosor y el ancho de banda, que se basa en el grosor del metal (27 nm) y el ancho de banda operativo (525 nm) propuesto en este trabajo.
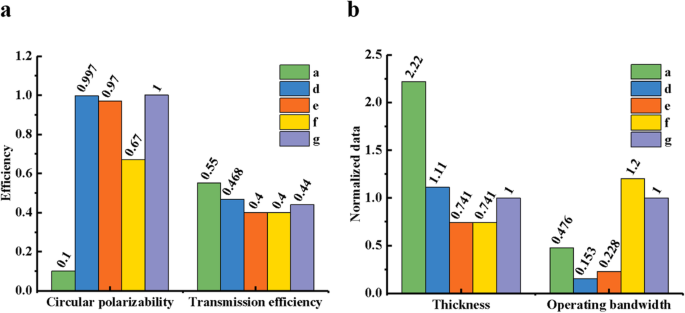
La comparación de las características de las estructuras mencionadas en la Tabla 1a, d, e, f y g. un La elipticidad de la polarización LTC y la transmisión total a 1550 nm. b El espesor de metal normalizado y el ancho de banda normalizado de la polarización CTL, según la estructura propuesta g
Al comparar las cinco estructuras mencionadas anteriormente, encontramos que, aunque la estructura a tiene la mayor eficiencia de transmisión y una banda ancha, es completamente imposible lograr una polarización circular a 1550 nm y tiene un grosor muy grande. La estructura d tiene la polarización circular más alta, una alta eficiencia de transmisión y el grosor ocupa el segundo lugar en cinco, pero el ancho de banda es muy estrecho. Este diseño puede lograr una buena polarización CTL y LTC a 1550 nm, pero no es adecuado para una placa de cuarto de onda con gran ancho de banda. Las placas de onda ultradelgadas eyf tienen el mismo grosor de 10 nm y la misma eficiencia de transmisión más baja. Sin embargo, si se compara la polarización circular, e es mejor que el rendimiento f, y el ancho de banda, f es mucho más mejor que e. Aunque la estructura f tiene la banda más ancha, los otros tres indicadores son los peores y es imposible lograr una polarización circular a 1550 nm. La estructura g no solo realiza las transformaciones LTC / CTL de manera eficiente y perfecta, sino que también tiene las características de un espesor pequeño y una banda de trabajo ancha. Este es el resultado de sopesar el rendimiento necesario de un cuarto de placa de onda. Combinando la tecnología de nanoprocesamiento existente con la literatura publicada, descubrimos que nuestro cuarto de placa de onda se puede preparar experimentalmente. En términos generales, podemos realizar el experimento en tres pasos:primero, se definen patrones en forma de rectángulo en la capa de resistencia ZEP520 mediante litografía por haz de electrones (EBL) sobre sustrato de sílice; en segundo lugar, se obtiene una matriz de estructura complementaria de supercélula de placa de onda de un cuarto por exposición a un haz de electrones; tercero, se deposita una fina capa de plata por evaporación del haz de electrones; último paso, elimine los materiales no deseados mediante un proceso de despegue o grabado. La referencia [25] utilizó el mismo procedimiento para preparar un cuarto de onda de nanovarillas de oro. El grosor de las nanovarillas de plata es de 60 nm y el ancho más estrecho es de 20 nm. La profundidad a la anchura es 3, lo que significa que es relativamente difícil de fabricar. La referencia [16] hizo un cuarto de placa de onda utilizando los mismos procesos. El espesor de la película de oro es de 35 nm y el espacio metálico más estrecho es de solo 10 nm. Aunque una inevitable falta de homogeneidad de espesor y pérdidas de material reducen la fuerza de resonancia en longitudes de onda más cortas, las mediciones concuerdan bien con las simulaciones. En este trabajo, el grosor de la capa plateada de la placa de ondas es de 27 nm, y la parte más estrecha es de 50 nm, la profundidad a ancho es de aproximadamente 0,5. Además, como se muestra en la imagen pequeña de la Fig. 2c, cuando el ancho de las aberturas W x aumenta de 80 a 100 nm, la longitud de onda operativa se cambia de 1545 (transmitancia de aproximadamente 0,432) a 1550 nm (transmitancia de aproximadamente 0,44). Significa que la estructura del artículo tiene una buena solidez y no se verá muy afectada por los errores experimentales.
Por lo tanto, la estructura de varias aberturas evita la idea de introducir una diferencia de fase anisotrópica por la estructura delgada (que es difícil de construir) y proporciona una nueva dirección para el diseño de la placa de cuarto de onda.
Conclusiones
Hemos considerado numéricamente una placa de cuarto de onda transmisiva de banda ancha realizable a una longitud de onda de comunicación, que tiene una matriz de períodos de orificios de sublongitud de onda en una película de plata de 27 nm de espesor. Al ajustar las resonancias plasmónicas, las resonancias dipolares eléctricas y las anomalías de Wood, puede lograr una amplia banda de polarización circular a lineal (525 nm) y una alta eficiencia de transmisión de 0.44, que está cerca del valor máximo teórico de 0.5 calculado por la teoría de la admitancia superficial. Especialmente a 1550 nm, la elipticidad es 1, que realiza perfectamente la conversión de polarización lineal a circular. A través del análisis, creemos que esta estructura puede funcionar bien como un cuarto de onda por su buena robustez. Se espera que se utilice en componentes ópticos miniaturizados como manipulación de polarización, detección óptica y funciones de comunicación.
Disponibilidad de datos y materiales
Los conjuntos de datos generados durante y / o analizados durante el estudio actual están disponibles de los autores correspondientes a solicitud razonable.
Abreviaturas
- CTL:
-
Circular a lineal
- LTC:
-
Lineal a circular
- FDTD:
-
Dominio del tiempo de diferencia finita
- θ i :
-
El ángulo de la onda incidente
- x-pol. :
-
polarización x
- y-pol. :
-
polarización y
- SiO 2 :
-
Sílice
- Ag:
-
Plata
- Au:
-
Oro
Nanomateriales
- Tutorial de colecciones de C# con ejemplos
- Tutorial de C# ArrayList con ejemplos
- Control completo de polarización de terahercios con ancho de banda ampliado a través de metauperficies dieléctricas
- Las propiedades eléctricas de los compuestos híbridos basados en nanotubos de carbono de paredes múltiples con nanoplaquetas de grafito
- Absorbedor perfecto de banda ancha con monocapa MoS2 y matriz de nanodiscos de nitruro de titanio hexagonal
- Sensor plasmónico basado en nanoprismas dieléctricos
- Alto rendimiento de PEDOT:células solares PSS / n-Si basadas en una superficie texturizada con electrodos AgNWs
- Modulador de electroabsorción de polarización de plasma superficial insensible a la polarización basado en óxido de estaño indio Epsilon-Near-Zero
- Convertidor de polarización con birrefringencia controlable basado en metauperficie híbrida de grafeno totalmente dieléctrico
- Transmisión unidireccional dependiente de pseudospin en cristales plasmónicos topológicos basados en grafeno
- Metasuperficies plasmónicas ópticamente activas basadas en la hibridación de acoplamiento en el plano y acoplamiento fuera del plano



