Transmisión unidireccional dependiente de pseudospin en cristales plasmónicos topológicos basados ​​en grafeno

Métodos

Investigamos la topología de bandas de los SPP en un cristal plasmónico 2D de una matriz de nanodiscos de grafeno dispuestos periódicamente rodeados por la misma hoja de grafeno con diferente potencial químico, como se muestra en la Fig. 1a. La constante de celosía a =40 nm, μ _c1 y r son el potencial químico y los radios de los nanodiscos de grafeno; μ _c2 denota el potencial químico del grafeno circundante. Al resolver las ecuaciones de Maxwells con condiciones de contorno, obtenemos la relación de dispersión para los modos SPP polarizados magnéticos transversales (TM) apoyados en la capa de grafeno rodeada por aire y sílice [29]:

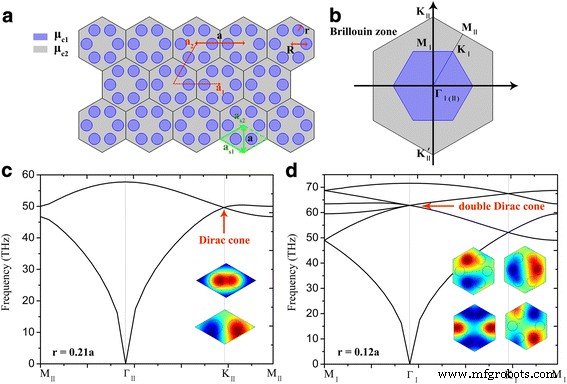
un Esquemas de los GPC 2D. b Las zonas de Brillouin. c Estructura de bandas de la red basada en la celda unitaria primitiva rómbica indicada con líneas discontinuas verdes, los recuadros trazan las distribuciones de campo eléctrico propio del punto de Dirac. d Estructura de banda de la celosía basada en la celda unitaria hexagonal, los recuadros trazan las distribuciones del campo eléctrico propio del punto doble de Dirac. Los otros parámetros se establecen como μ _c1 =0,3 eV, μ _c2 =0,6 eV, τ =1 ps, la constante de celosía a =40 millas náuticas

Aquí, ε ₀ es la permitividad del vacío del espacio libre, k ₀ =2π / λ es el número de onda en el espacio libre, y λ es la longitud de onda operativa en el vacío. En la región del infrarrojo medio, se supone que las constantes dieléctricas del aire y la sílice correspondientes a los super y sustratos son ε _Aire =1 y ε _SiO2 =3,9 respectivamente [30]. En el régimen no retardado donde β » k ₀ , la Eq. (3) se puede simplificar a [31].

donde β es la constante de propagación SPP en la capa de grafeno y el índice de refracción efectivo n _ef del modo SPP se puede derivar de n _ef = β / k ₀ . σ _g es la conductividad superficial del grafeno compuesta por las contribuciones de intrabanda e interbanda, es decir, σ _g = σ _intra + σ _entre [29, 30]. La conductividad intrabanda σ _intra correspondiente al proceso de dispersión de electrones-fotones intrabanda viene dado por

donde μ _c es el potencial químico relacionado con la densidad de electrones, e es la carga del electrón, ω es la frecuencia angular del plasmón, ℏ y k _B son la constante de Planck reducida y la constante de Boltzmann respectivamente, T es la temperatura y τ representa el tiempo de relajación del impulso electrónico debido a la dispersión del portador de carga. Para ℏω » k _B T y | μ _c | » k _B T , la conductividad entre bandas σ _entre correspondiente a las transiciones de electrones entre bandas se puede expresar aproximadamente como

Resultados y discusión

Las estructuras de bandas de energía de los cristales plasmónicos propuestos se obtienen empleando el método de elementos finitos (FEM) basado en el software COMSOL Multiphysics disponible comercialmente. En la Fig. 1a, notamos que tanto la celda unitaria rómbica de dos nanodiscos de grafeno (rombo punteado verde definido por los vectores a _s1 y un _s2 ) y la celda unitaria hexagonal de seis nanodiscos de grafeno (con vectores de celosía a ₁ y un ₂ ) pueden formar los cristales plasmónicos en forma de panal. La Figura 1b presenta las BZ para las celdas unitarias rómbicas y hexagonales, con las zonas irreducibles de M _II - Γ _II - K _II - M _II y M _I - Γ _Yo - K _I - M _I respectivamente. Tenga en cuenta que la celda unitaria hexagonal es tres veces más grande que la primitiva rómbica. Por lo tanto, la primera BZ de la celda unitaria primitiva rómbica es tres veces mayor que la de la hexagonal (región azul en la Fig. 1b). Al tomar una celda unitaria primitiva rómbica, este cristal plasmónico exhibe una dispersión del cono de Dirac en K _II y K _II `puntos en las esquinas BZ como se muestra en la Fig. 1c. Los recuadros de la Fig. 1c muestran las distribuciones propias del campo eléctrico de los dos estados degenerados en el punto de Dirac. De manera similar a los pseudo-espines en los sistemas fotónicos y acústicos clásicos [17, 19, 20], para imitar el análogo de los pseudo-espines en el sistema plasmónico, el grado de libertad debe aumentarse a dos estados. Por lo tanto, se requieren conos de Dirac dobles degenerados cuádruple en la estructura de la banda plasmónica. Empleando el mecanismo de plegado de zona [18], los conos de Dirac en K <sub>II</sub> y K <sub>II</sub> `los puntos se doblan en un cono de Dirac doble en Γ punto en el centro BZ al tomar la celda unitaria hexagonal más grande (como se muestra en la Fig. 1d). Los recuadros de la Fig. 1d muestran los estados propios degenerados cuádruples con modos dipolo y cuadrupolo. Los parámetros relativos que usamos son μ _c1 =0,3 eV, μ _c2 =0,6 eV y τ =1 ps, que se eligen moderadamente de las investigaciones anteriores para el grafeno práctico [32, 33].

Los conos de Dirac dobles degenerados cuádruples compuestos por dos modos dipolares y dos cuadrupolares están asociados con dos representaciones 2D irreductibles de un C _6v grupo de puntos, es decir, E ₁ modos de paridad espacial impar y E ₂ modos de paridad espacial uniforme. Siguiendo la notación convencional ampliamente adoptada en mecánica cuántica [34], podemos clasificar estos modos en p _x / p _y y d _x2-y2 / d _xy modos de acuerdo con su propia E _z distribuciones de campo que se muestran en la Fig. 2. A continuación, para abrir una brecha de banda topológica no trivial en el Γ punto, tomamos modificaciones adicionales (es decir, deformar la celosía en forma de panal de a / R =3) en la celda unitaria hexagonal para romper la simetría. Al reducir los nanodiscos de grafeno a a / R =3.2, el cono de Dirac doble degenerado cuádruple se divide en dos estados degenerados dobles y se abre una banda prohibida a granel de 62.1 a 63.5 THz como se muestra en la Fig. 2a. El E _z Los campos de las bandas inferiores tienen un par de modos dipolo que muestran p _± caracteres, mientras que las bandas superiores tienen un par de modos de cuadrupolo que muestran d _± personajes alrededor del Γ punto, que es consistente con la teoría fotónica clásica de que los modos dipolo deben exhibir una frecuencia más baja que los modos cuadrupolo de orden superior. Sin embargo, se produce una inversión de banda cuando se expanden los nanodiscos de grafeno a a / R =2,9, es decir, los modos dipolo se elevan por encima de los modos cuadrupolo, lo que provoca la banda prohibida topológica no trivial de 62,4 a 63,3 THz como se muestra en la Fig. 2c. La Figura 2d, e ilustra el proceso de transición topológica entre p _± y d _± estados, y los campos magnéticos en el plano asociados con p _± y d _± están marcados con flechas blancas. Los momentos angulares de la función de onda de E _z campos p _± =( p _x ± i p _y ) / \ (\ sqrt {2} \) y d _± =( d _x2-y2 ± i d _xy ) / \ (\ sqrt {2} \) constituyen además la pseudoespina en los presentes cristales plasmónicos [17, 18].

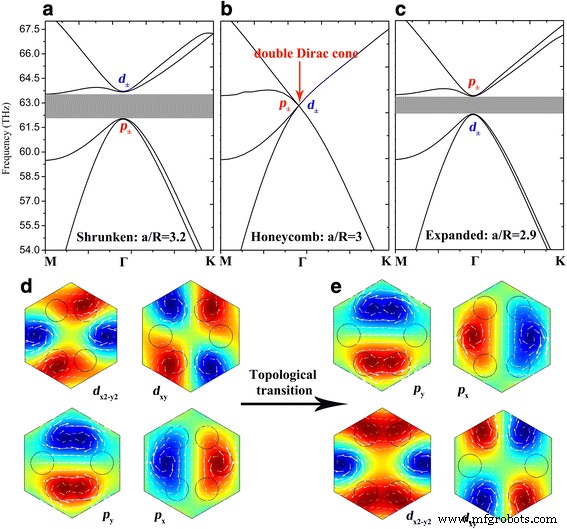
Estructuras de bandas de los GPC con a a / R =3.2, b a / R =3 y c a / R =2,9. d , e El E _z distribuciones de campo de los modos dipolo y cuadrupolo de la p _± y d _± estados en a y c respectivamente. Las flechas blancas presentan el campo magnético en el plano asociado con E _z campo

Para explorar más a fondo la propiedad topológica de los huecos de banda mostrados en la Fig. 2a, c, generalmente se relaciona con una descripción hamiltoniana eficaz y números topológicos. Al aplicar la teoría de perturbación \ (\ overset {\ rightharpoonup} {k} \ cdot \ overset {\ rightharpoonup} {p} \), la H eficaz de Hamilton _ef ( k ) alrededor de Γ punto sobre la base [ p ₊ , d ₊ , p _- , d _- ] se puede expresar como [17, 35].

donde k _± = k _x ± i k _y y A proviene de elementos fuera de la diagonal del término de perturbación de primer orden \ ({M} _ {\ alpha \ beta} =\ left \ langle {\ Gamma} _ {\ alpha} \ left | \ overset {\ rightharpoonup} {k } \ cdot \ overset {\ rightharpoonup} {p} \ right | {\ Gamma} _ {\ beta} \ right \ rangle \) con α =1, 2 y β =3, 4. La H eficaz hamiltoniana _ef ( k ) adopta una forma similar a la del modelo de Bernevig-Hughes-Zhang (BHZ) para el sistema de pozos cuánticos CdTe / HgTe / CdTe [36], lo que implica una banda prohibida topológica cuando tiene lugar la inversión de banda. Basado en el hamiltoniano expresado en Eq. (5), podemos evaluar los números de spin Chern de los cristales plasmónicos topológicos como [36].

Aquí, M =( E _p - E _d ) / 2 es la diferencia de frecuencia entre E ₂ y E ₁ representaciones en el Γ punto. B está determinada por los elementos diagonales del término de perturbación de segundo orden y suele ser negativa [19]. Por lo tanto, C _± =0 se obtiene cuando se tiene un orden de banda normal como se muestra en la Fig. 2a. Y llegamos a la conclusión de que la banda prohibida abierta es trivial. Sin embargo, M se vuelve positivo cuando se produce la inversión de la banda. Por lo tanto, C _± =± 1 simplemente se obtiene, y la brecha en la Fig. 2c no es trivial.

Al superponer los huecos de banda con diferentes topologías (es decir, topológico trivial y topológico no trivial), se pueden crear estados de borde que están espacialmente confinados alrededor de la interfaz entre dos cristales plasmónicos. Aquí, consideramos una cinta de cristal plasmónico topológicamente no trivial (con la estructura de banda mostrada en la Fig. 2c) con sus dos bordes revestidos por dos cristales plasmónicos topológicamente triviales (con la estructura de banda mostrada en la Fig. 2a) en la misma ventana de frecuencia. Las dos regiones triviales evitan que los posibles estados de borde se filtren al espacio libre. En la Fig. 3a, presentamos las estructuras de bandas proyectadas calculadas a lo largo de Γ Dirección K para una cinta de este tipo, donde una banda prohibida a granel está atravesada por estados de borde topológicos adicionales como lo indican las curvas rojas degeneradas dobles. La Fig. 3b traza las distribuciones del campo eléctrico confinadas alrededor de la interfaz construida por dos cristales distintivos, correspondientes a los puntos A (con k _x =- 0.05π / a ) y B (con kx =0.05π / a ) marcado en la Fig. 3a. Las características de pseudo spin-up y spin-down se evidencian por vórtices de fase en sentido antihorario y horario, como se ilustra en el panel derecho de la Fig. 3b.

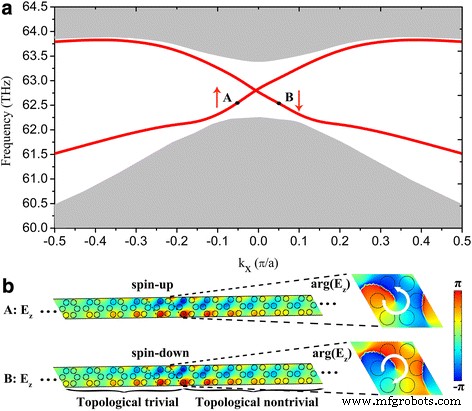
un Estructura de banda proyectada para una supercélula compuesta por 16 celdas unitarias no triviales revestidas por 12 celdas unitarias triviales en ambos lados. b Distribuciones de campo eléctrico alrededor de la interfaz entre los cristales plasmónicos triviales y no triviales en los puntos A y B, es decir, en k _x =- 0.05π / ay 0.05π / a respectivamente

La transmisión unidireccional dependiente de pseudospin de los estados de borde también se demuestra en un finito 20 a × 18 a celosía construida por los cristales triviales y no triviales. Como se muestra en la Fig. 4a, b, propagación unidireccional de la onda SPP hacia la dirección izquierda (derecha) cuando es excitada por una fuente de pseudo spin-up (spin-down) S ₊ ( S _- ) de polarización circular en sentido antihorario (sentido horario) del campo magnético en el plano. Una de las características más distintivas de los estados de borde topológicos es que son robustos contra perturbaciones / imperfecciones. Para verificar esta robustez, construimos curvas pronunciadas como se muestra en la Fig. 4c, donde la transmisión unidireccional de la onda SPP es excitada por una fuente pseudo-spin-down S _- . La onda SPP desapareció finalmente después de una larga distancia de viaje a lo largo de las curvas pronunciadas debido a la pérdida intrínseca de material de grafeno. Para confirmar aún más esta transmisión topológica, también exhibimos la distribución de la intensidad del campo eléctrico ignorando la pérdida intrínseca de grafeno para la comparación. Como puede verse en la Fig. 4d, la onda SPP sigue la ruta diseñada y mantiene la propagación unidireccional con poca retrodispersión.

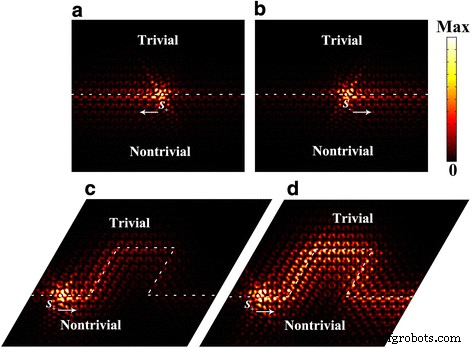
un Hacia la izquierda y b estados de borde unidireccionales hacia la derecha excitados por un campo magnético en el plano con una diferencia de fase π / 2:\ ({S} _ {\ pm} ={H} _0 \ left (\ overset {\ rightharpoonup} {x} \ mp i \ overset {\ rightharpoonup} {y} \ right) \). c Estados de bordes topológicos que viajan a lo largo de curvas cerradas. d La distribución de la intensidad del campo eléctrico de la transmisión topológica unidireccional sin considerar la pérdida intrínseca de material de grafeno

Conclusiones

En resumen, hemos investigado sistemáticamente las topologías de banda de los GPC construidos por nanodiscos de grafeno con patrones periódicos. Al emplear un mecanismo de plegado por zonas, los conos de Dirac en la esquina BZ se pliegan en un cono de Dirac doble en el centro de BZ. Además, los huecos de la banda topológica se obtienen deformando los GPC de celosía en forma de panal. Con base en el hamiltoniano efectivo derivado de la teoría de perturbación \ (\ overset {\ rightharpoonup} {k} \ cdot \ overset {\ rightharpoonup} {p} \), se evalúan los números de espín Chern. Las características de pseudoespín, evidenciadas por vórtices de fase de sentido antihorario y horario, se utilizan con éxito para realizar la transmisión unidireccional de estados de borde a lo largo de una interfaz construida por dos cristales plasmónicos topológicos triviales y no triviales. El GPC diseñado proporciona un nuevo camino para investigar los fenómenos topológicos y puede encontrar aplicaciones potenciales en los campos de la plasmónica topológica. También podría desencadenar la exploración de los plasmónicos de pseudospin y la técnica de multiplexación de pseudospin en circuitos integrados nanofotónicos de alta densidad.

Abreviaturas

BHZ:

Bernevig-Hughes-Zhang

BZ:

Zona de Brillouin

FEM:

Método de elementos finitos

GPC:

Cristal plasmónico de grafeno

QHE:

Efecto Hall cuántico

QSHE:

Efecto Hall de giro cuántico

SPP:

Polaritones de plasmón de superficie

Nanocristal de Sb2O3 dopado con S:un catalizador de luz visible eficiente para la degradación orgánica Estudio comparativo de las propiedades electroquímicas, biomédicas y térmicas de nanomateriales naturales y sintéticos