Cambio en la conductividad superficial de cristales de p-Si deformados elásticamente irradiados por rayos X
Resumen
En este artículo se investigaron los cambios en la conductividad de los monocristales de p-Si irradiados y no irradiados bajo la influencia de la tensión mecánica uniaxial elástica. Se sugirió una expresión analítica para describir la dependencia de la conductividad de la superficie en función de la tensión mecánica y la dosis de irradiación de rayos X. Se demostró que las nanopartículas de 4 ángulos en la superficie del silicio "solar" afectan los cambios de electroconductividad bajo estrés mecánico. Se estableció que la irradiación de rayos X provoca la generación de defectos puntuales en el silicio. Estos defectos suprimen el movimiento de las dislocaciones. Se demostró que la resistividad de muestras de silicio "electrónico" previamente irradiadas es solo ligeramente sensible a la influencia de la compresión uniaxial a cierta velocidad de deformación.
Antecedentes
Un uso generalizado de dispositivos semiconductores en el campo de las tecnologías electrónicas modernas requiere la investigación de nuevos materiales semiconductores que posean una alta estabilidad bajo la influencia externa, como la irradiación de rayos X y la deformación mecánica. Hoy en día, el silicio se utiliza activamente en detectores de alta sensibilidad y otros sensores semiconductores que operan en los campos de radiación [1].
La mayoría de los artículos están dedicados al impacto de la deformación plástica en la conductividad del n-Si [2, 3]. Es por eso que el impacto de la deformación elástica en las propiedades de los cristales de p-Si todavía se considera una tarea científica importante. La redistribución de la concentración de portadores y las impurezas en los cristales deformados se caracteriza a menudo por la presencia de dislocaciones que son eliminadores eficaces de defectos, especialmente en la superficie del cristal [4, 5]. Se sabe [3, 6] que la excitación de los subsistemas electrónicos cristalinos también va acompañada de los correspondientes cambios en la movilidad de la dislocación. La excitación de los subsistemas electrónicos podría deberse a una influencia externa, como la radiación y el campo electrostático. Un rasgo característico de las dislocaciones en los cristales de silicio es la presencia de defectos puntuales (nube de Cottrell) con una alta concentración alrededor de las dislocaciones.
La superficie de los cristales es la más sensible a las radiaciones ionizantes. Es por eso que la investigación de los procesos inducidos por radiación en las capas superficiales de los cristales de silicio todavía se considera relevante. La superficie con los contactos de Al depositados es un eliminador eficaz de los defectos estructurales [5,6,7]. Debajo de la película metálica depositada, las tensiones mecánicas aparecen debido a inconsistencias en los parámetros de la red de la película y el semiconductor [5, 7]. Estas tensiones estimulan los procesos de obtención de defectos (átomos de impurezas, átomos de silicio intersticiales y vacantes) en la capa de contacto.
Métodos
Monocristales de silicio de conductividad tipo p, cultivados por el método de Czochralski ( ρ =10-20 Ω cm), se utilizaron en el artículo de investigación. Estos monocristales son de dos tipos:(1) silicio para electrónica:los llamados monocristales sin dislocación (o electrónicos) en la superficie (111) de los cuales, la concentración de picaduras triangulares de grabado no excede 10 2 cm −2 (Figs. 1a y 2), y (2) monocristales “solares” de silicio en la superficie (111) de los cuales, los defectos en forma de pirámides de 4 ángulos (Fig. 1b) fueron descubiertos debido a una relativamente gran concentración del carbono de fondo (≈5 × 10 16 cm −3 ) y oxígeno (≈1,8 × 10 18 cm −3 ) impurezas. Las pirámides de cuatro ángulos se ubican de la misma manera. El tamaño de la base de la pirámide es de 10 nm a 10 μm.
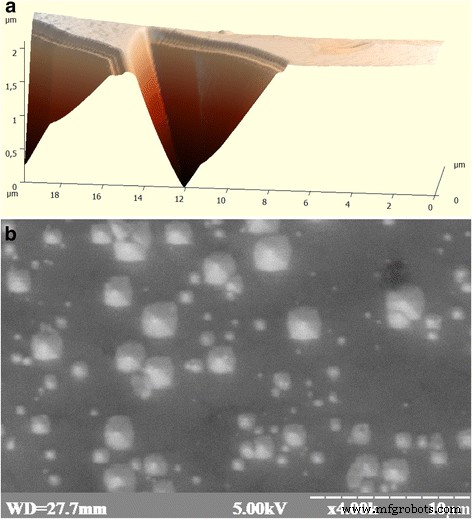
El aspecto de la superficie de las muestras experimentales: a aparición de picaduras de dislocación en la superficie del cristal de p-Si obtenido en el campo del microscopio de fuerza atómica y b apariencia de la superficie submicroscópica (111) de cristales solares
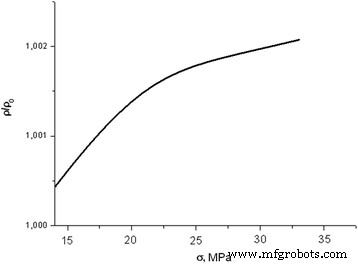
Dependencia de la resistencia longitudinal de la muestra primaria libre de dislocaciones durante la deformación elástica con una tasa de deformación de 8 μm / min
Se demostró [8, 9] que en la formación de clusters, a los que corresponden agujeros de grabado piramidal de 4 ángulos, pueden participar capas de óxido de silicio, defectos puntuales y capas con diferentes estados estructurales de silicio, particularmente silicio alfa.
Las muestras experimentales obtuvieron dimensiones de 4 × 3,7 × 7,6 mm después del lijado y pulido químico. Los contactos óhmicos en forma de dos tiras con un ancho de 1,5 mm en los extremos de las superficies de la muestra (111) se crearon por evaporación térmica del aluminio al vacío (10 −4 Pa) a una muestra calentada a 593 K. La medición de la conductividad eléctrica se realizó en un criostato de vacío a una presión de gas residual 10 −3 Pa en la aplicación de compresión uniaxial en los extremos (hacia [\ (11 \ overline {2} \)]) con una potencia de 15 a 40 MPa y una tasa de deformación de 8 o 32 μm / min. Las muestras se irradiaron con una gama completa de radiación X ( W -anodo, 50 kV, 10 mA), en ambos lados, sobre los que se recubrieron contactos de aluminio. La distancia entre la fuente de rayos X y los cristales fue mínima (1-2 mm). Se encontró que la dosis absorbida aumentaba en 130 Gy cada 30 min. En el trabajo, primero irradiamos las muestras experimentales y, posteriormente, medimos la resistencia en el proceso de deformación.
Resultados y discusión
El resultado de la investigación sobre el cambio de conductividad mecánica inducida a lo largo de la dirección de deformación ( ρ ( σ )) de muestras "libres de dislocaciones" de conductividad de tipo p bajo la influencia de tensión uniaxial ( σ ) se muestra en la Fig. 2. El aumento de la carga de 0 a 40 MPa (a una tasa de deformación de 8 μm / min) dura 45 min.
En el proceso de deformación, la resistencia de las muestras libres de dislocaciones aumenta ligeramente. Cabe señalar que en el caso de los cristales no irradiados, el cambio de la tasa de deformación prácticamente no tuvo efecto en la visión general de las dependencias ρ ( σ ) [10, 11]. Se obtuvieron dependencias similares para las muestras irradiadas (Fig. 3). Se observó un aumento de la resistencia después de la acción de la irradiación X. Sin embargo, la naturaleza de la dependencia ρ ( σ ) se observó que era algo diferente a las muestras no irradiadas.
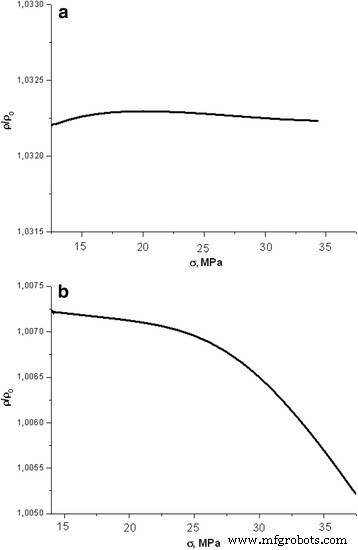
Dependencia de la resistencia longitudinal de irradiados ( D =130 Gy) muestra de silicio sin dislocaciones durante la deformación elástica con una fuerza de compresión creciente a una velocidad de 8 μm / min ( a ) y 32 μm / min ( b )
Puede verse que la resistencia permanece prácticamente inalterable (Fig. 3a) durante la compresión a una velocidad de 8 μm / min debido al efecto de la irradiación X. Los gráficos de dependencias de muestras expuestas a 260 y 480 Gy tenían un aspecto similar. En estudios anteriores [11] se demostró que la resistencia aumentaba proporcionalmente a la raíz cuadrada de la dosis absorbida durante el proceso de irradiación.
Un aumento de cuatro veces en la tasa de compresión (de 8 a 32 μm / min) conduce a cambios en la naturaleza de la dependencia de la resistividad de la carga (Fig. 3b). Hay una pequeña disminución (<0,2%) en la resistencia de las muestras irradiadas en el proceso de compresión. Cabe señalar que todas las mediciones de los cambios de conductividad se llevaron a cabo con un alto grado de precisión (± 0,045%) de modo que fue posible analizar correctamente los pequeños cambios de resistividad en el experimento.
Cabe señalar que la dependencia, mostrada en la Fig.3, se ha recibido 7 días después de la medición de cambios en la resistencia longitudinal ( D =130 Gy) de muestras sin dislocación a una velocidad de 8 μm / min (Fig. 3a). Durante el período de tiempo dado, la resistencia casi volvió a su valor original, es decir, el valor de la resistencia, que se observó después de la irradiación y la aplicación de tensión mecánica.
También se realizaron estudios similares sobre la medición de la dependencia de la resistencia de la acción de la compresión elástica y después de la exposición a la radiación (Fig. 4) para muestras experimentales basadas en "silicio solar" de conductividad tipo p, a las que son inherentes pirámides de 4 ángulos en la superficie (111).
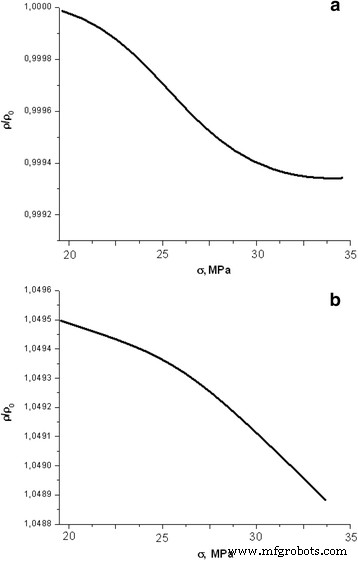
Dependencia de la resistencia longitudinal del silicio solar durante la deformación elástica con una fuerza de compresión creciente: a D =0 Gy, velocidad de compresión 32 μm / min; b D =130 Gy velocidad de compresión 8 μm / min
En primer lugar, se encontró que la naturaleza del cambio de resistencia del silicio "solar" de tipo p-Si sobre el tamaño de la tensión mecánica es independiente de la velocidad de compresión. Se observó una característica similar tanto en muestras irradiadas como no irradiadas. Las dependencias de la resistencia longitudinal de la tensión mecánica cambian en un valor relativamente pequeño (<0,5%), y disminuye ligeramente con el aumento de la carga (Fig. 4a).
La irradiación de muestras experimentales con rayos X (480 Gy) no afecta virtualmente la naturaleza general del cambio en la resistencia longitudinal del silicio "solar" durante la deformación elástica (Fig. 4b). En cuanto a las muestras electrónicas, la resistencia es proporcional a la raíz cuadrada de la dosis absorbida [11]. Durante el esfuerzo mecánico, la resistividad disminuye en un valor muy pequeño (± 0.1%).
Como se demostró en nuestros estudios anteriores [12, 13], la película dieléctrica SiO 2 tiene carga positiva. Por tanto, la capa superficial de carga espacial agotada en huecos (con alta resistencia) y con un espesor w (Fig. 5) se crea en silicio. Cuanto más cerca esté el Si-SiO 2 a la interfaz, menos agujeros hay.
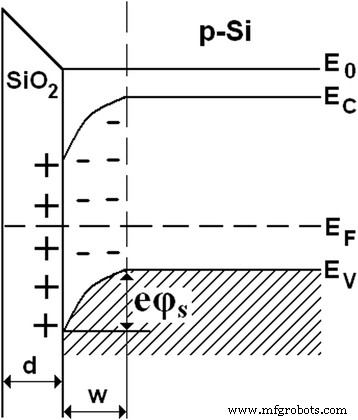
Distorsión de las bandas de energía en el conductor tipo p bajo carga positiva proporcionada en la interfaz del semiconductor-aislante
La concentración de agujeros en la capa superficial de silicio y, en consecuencia, su conductividad cambia en caso del cambio de potencial superficial ( φ S ). Consideremos una placa cuadrada plana (Fig. 6). Deje que la corriente fluya paralela al plano de la placa en la dirección de uno de sus bordes.
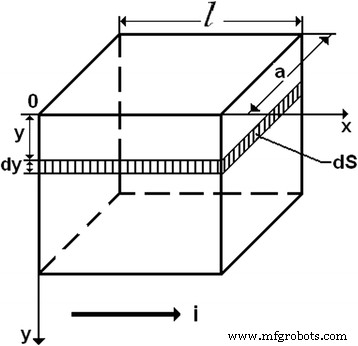
Cálculos de conductividad
Se tomó una fina capa paralela con espesor dy y área de la sección transversal dS [14] a cierta distancia ( y ) desde la superficie. Esta capa se puede considerar como un semiconductor homogéneo, cuya resistencia se puede determinar de acuerdo con la siguiente fórmula:
$$ d R =\ rho \ frac {l} {dS}, $$ (1) $$ d S =a d y. $$ (2)Dado que la placa es cuadrada ( l = a ), la conductividad de la capa es
$$ d \ lambda =\ frac {1} {dR} =\ sigma d y, $$ (3)donde \ (\ sigma =\ frac {1} {\ rho} \) es la conductividad eléctrica de la capa con dy espesor en y distancia de la superficie. Para un semiconductor de tipo p, la conductividad se puede escribir como \ (\ sigma \ approx e p (y) {\ mu} _p \). Entonces obtenemos
$$ d \ lambda =e p (y) {\ mu} _p dy. $$ (4)Encontremos la conductividad superficial total ( λ ). Debe integrar la última expresión en el rango de cero a un grosor de varios tramados Debye sostenibles o, por ejemplo, restringir el ancho de la región de carga espacial w :
$$ \ lambda ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} ep (y) {\ mu} _p dy =e {\ mu} _p {\ displaystyle \ underset {0} { \ overset {w} {\ int}} p (y) dy}}. $$ (5)En general, la concentración de huecos en la capa superficial empobrecida depende no solo de las coordenadas ( y ) sino también sobre la tensión mecánica aplicada ( σ meh ). Está determinada por dos componentes: p ( y , σ meh ) = p 1 ( y ) - p 2 ( σ meh ), donde p 1 ( y ) es un componente que corresponde a un cambio en la concentración del portador con el cambio de distancia desde la superficie del semiconductor y p 2 ( σ meh ) es un componente que muestra cuánto se reduce la concentración de agujeros debido a su captura en las dislocaciones durante el esfuerzo mecánico. Además, la movilidad de los agujeros no es un valor constante. Depende de la tensión mecánica. Por lo tanto, la expresión para la conductividad superficial total se puede escribir de la siguiente forma:
$$ \ lambda =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) {\ displaystyle \ underset {0} {\ overset {w} {\ int}} \ left ({p} _1 (y) - {p} _2 \ left ({\ sigma} _ {meh} \ right) \ right) dy}. $$ (6)El cambio de conductividad inducido mecánicamente se puede escribir de la siguiente manera:
$$ \ lambda \ left ({\ sigma} _ {meh} \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) \ cdot \ Big ({\ displaystyle \ underset { 0} {\ overset {w} {\ int}} {p} _1 (y) dy - {\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _2 \ left ({\ sigma} _ {meh} \ right) dy} \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) \ cdot \ left \ {{\ beta} _1 - {\ beta } _2 \ left ({\ sigma} _ {meh} \ right) \ right \}}, $$ (7)donde \ ({\ beta} _1 ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 (y) dy; \ kern1em {\ beta} _2 \ left ({\ sigma } _ {meh} \ right) ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _2 \ left ({\ sigma} _ {meh} \ right) dy}} ={p} _2 \ left ({\ sigma} _ {meh} \ right) {\ displaystyle \ underset {0} {\ overset {w} {\ int}} dy =} w \ cdot {p} _2 \ left ( {\ sigma} _ {meh} \ derecha) \).
Cabe señalar que desde p 1 ( y ) y p 2 ( σ meh ) también dependen del efecto de la irradiación, los factores β 1 , β 2 y μ p dependen de la dosis de irradiación X. Por lo tanto, la fórmula para la conductividad superficial antes de ( λ ( σ meh , 0 )) y después ( λ ( σ meh , D )) la irradiación se puede escribir de la siguiente manera:
$$ \ lambda \ left ({\ sigma} _ {meh}, 0 \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh}, 0 \ right) \ cdot \ Big ({\ Displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, 0 \ right) dy- w \ cdot {p} _2 \ left ({\ sigma} _ {meh} , 0 \ right) \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh}, 0 \ right) \ cdot \ left \ {{\ beta} _1 (0) - {\ beta} _2 \ left ({\ sigma} _ {meh}, 0 \ right) \ right \}}. $$ (8) $$ \ lambda \ left ({\ sigma} _ {meh}, D \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right) \ cdot \ Big ({\ Displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, D \ right) dy- w \ cdot {p} _2 \ left ({\ sigma } _ {meh}, D \ right) \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right) \ cdot \ left \ {{\ beta} _1 (D) - {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) \ right \}}. $$ (9)Si la muestra tiene una forma rectangular con una longitud ( l ) y ancho ( a ), podemos escribir la fórmula final para la conductividad superficial total de la siguiente manera:
$$ \ lambda \ left ({\ sigma} _ {meh}, D \ right) =\ frac {a} {l} e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right ) \ left \ {{\ beta} _1 (D) - {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) \ right \}, $$ (10)donde
$$ {\ beta} _1 (D) ={\ Displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, D \ right) dy, \ kern1em} {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) =w \ cdot {p} _2 \ left ({\ sigma} _ {meh}, D \ right). $$ (11)El cambio de conductividad superficial de los cristales de p-Si irradiados bajo la influencia de la tensión mecánica se determina principalmente por el cambio de tres parámetros: β 1 , β 2 y μ p .
Según nuestros estudios previos, [10,11,12,13], el efecto de la exposición de rayos X al silicio electrónico se acompaña de un ligero aumento en la carga positiva en la capa superficial dieléctrica de SiO 2 . Como resultado, el factor β 1 : β 1 ( D )> β 1 ( 0 ) aumenta ligeramente. Para el silicio "solar", se observan dependencias opuestas: β 1 ( D ) < β 1 ( 0 ).
Respecto al factor β 2 , sus cambios están determinados principalmente por el cambio de p 2 ( σ meh , D ) bajo efecto de radiación. Estos cambios son mucho más sustanciales en comparación con el cambio del parámetro β 1 . La irradiación X desencadena la generación de defectos puntuales en el silicio, que actúan como topes para el movimiento de dislocación. Como resultado, después de la exposición a la radiación, el factor β 2 para estas muestras disminuye drásticamente (reduce el número de orificios atrapados por dislocación) para ambos tipos de muestras experimentales p-Si: β 2 ( D ) < β 2 ( 0 ).
En los cristales de silicio “solar” no irradiados, los defectos existentes, a los que corresponden las picaduras piramidales de 4 ángulos, desempeñan el papel de tapones para el movimiento de dislocación. Los defectos adicionales generados por la irradiación no jugaron un papel significativo en el contexto de una fuerte concentración de defectos superficiales existentes.
La movilidad de los agujeros se reduce ligeramente durante la exposición a la radiación debido al aumento de la dispersión en los defectos de radiación: μ p ( D ) < μ p ( 0 ). Mediante este mecanismo se puede explicar la disminución confirmada experimentalmente de la conductividad de las muestras de silicio irradiadas. Así, un análisis de las fórmulas (8) y (9) confirma el crecimiento de la resistencia bajo el aumento del valor de la dosis absorbida de irradiación X principalmente al reducir la movilidad ( μ p ( D ) < μ p ( 0 )) y la concentración de portadores de carga gratuita:huecos ( β 2 ( D ) < β 2 ( 0 )).
Si consideramos los datos de la ecuación a una dosis fija, podemos sacar las siguientes conclusiones, que confirman las dependencias experimentales dadas anteriormente de la resistencia a la tensión mecánica:
- 1.
La resistencia de las muestras no irradiadas de silicio electrónico aumenta bajo compresión (Fig. 2). Esto ocurre debido al crecimiento significativo del factor β 2 bajo la acción de tensión mecánica. Durante la compresión, el cambio (crecimiento) del factor β 2 excede significativamente el cambio (aumento) en la movilidad de los orificios bajo el aumento de la tensión mecánica. En cuanto al parámetro β 1 , su valor no depende de σ meh .
Entonces, en nuestro caso, el aumento de la resistencia (compresión) y la disminución (descompresión) de la carga de los cristales no irradiados basados en silicio electrónico puede explicarse por el movimiento de las dislocaciones, que se están apoderando de los principales portadores. Las fuerzas que provocan el movimiento de los defectos, la coagulación de los racimos y la condensación de los racimos en las dislocaciones [15] aparecen en la red cristalina deformada elásticamente. Los defectos se están convirtiendo en centros de captura de portadores principales mientras se coagulan en grupos más grandes como microporos, grupos de silicio de entrenudo e impurezas. La acumulación de defectos en la capa superficial de silicio tiende a reducir su conductividad. Se muestra por el factor de crecimiento correspondiente β 2 en la fórmula de la conductividad superficial.
- 2.
La resistencia de las muestras irradiadas de silicio electrónico cambia ligeramente bajo compresión (Fig. 3a). Esto es causado por la reducción del cambio (crecimiento) del factor β 2 , debido a un movimiento de dislocación impedido. En otras palabras, cambios de parámetros que compiten mutuamente β 2 y μ p son proporcionales a la compresión de muestras irradiadas de silicio electrónico.
La reducción de la resistencia de los cristales electrónicos de silicio en combinación con el aumento de la tensión (Fig. 3b) se produce debido a la disminución de la masa efectiva longitudinal de los agujeros pesados [16, 17] y al correspondiente aumento de su movilidad bajo compresión. Esto se muestra mediante el aumento de movilidad correspondiente μ p en la fórmula de la conductividad superficial.
- 3.
La resistencia de las muestras de silicio solar irradiadas y no irradiadas disminuye ligeramente bajo compresión (Fig. 4). El proceso de movimiento de dislocación es muy difícil para estas muestras experimentales. Además, los defectos adicionales que se mueven desde el centro hacia la superficie del silicio hacen una contribución no esencial al transporte de corriente en el contexto de una alta concentración de defectos superficiales existentes en los cristales de silicio solar. La acción de la radiación aumenta adicionalmente la concentración de defectos superficiales en cristales de silicio solar. Por lo tanto, los cambios de parámetros β que compiten mutuamente 2 y μ p son proporcionales a la compresión de muestras de silicio solar irradiadas y no irradiadas.
El efecto de la radiación (Fig. 4b) aumenta adicionalmente la concentración de defectos superficiales en los cristales de silicio solar. Por lo tanto, los defectos adicionales, que se mueven debido al gettering, hacen una pequeña contribución al transporte de corriente que en el caso de los cristales no irradiados.
Conclusiones
Se deben considerar dos factores principales que afectan la resistencia del cristal de p-Si durante la carga mecánica. El primer factor es un aumento de la resistencia con un aumento de la carga (compresión) y una disminución de la resistencia con una disminución de la carga (desacoplamiento) debido al proceso de movimiento de las dislocaciones, que se está apoderando de los principales portadores. El segundo factor es la disminución de la resistencia de los cristales de silicio con un aumento de carga debido a la disminución de la masa efectiva de los agujeros y el correspondiente aumento de su movilidad.
La irradiación de rayos X provoca la generación de vacantes y átomos intersticiales en el silicio, que actúan como tapones para el movimiento de dislocaciones. Debido al aumento de la dispersión de los defectos de radiación, la movilidad de los orificios disminuye ligeramente durante la irradiación de rayos X. En los cristales de silicio solar no irradiados, los defectos existentes juegan el papel de tapones para el movimiento de las dislocaciones.
Los cristales experimentales de p-Si preirradiados (silicio electrónico y "solar") tienen la propiedad de cambiar ligeramente su resistividad (± 0,2%) bajo la influencia de la compresión uniaxial (velocidad de suministro de tensión 8 μ / min), dentro de la deformación elástica a lo largo de la corriente [\ (11 \ overline {2} \)].
En las muestras electrónicas de p-Si preirradiadas, la dependencia de la resistencia de la tensión mecánica uniaxial depende significativamente de la tasa de compresión. A una baja velocidad de suministro de tensión (8 μm / min), la resistencia aumenta con el aumento de la tensión mecánica; a altas velocidades (32 μm / min), disminuye. Para cristales basados en silicio solar de tipo p, la dependencia de la resistencia bajo carga mecánica es independiente de la tasa de compresión.
Abreviaturas
- ρ ( σ ):
-
El cambio de conductividad mecánica inducida a lo largo de la dirección de deformación
Nanomateriales
- Silicio
- Cambiar máquina
- Imágenes de átomos en cristales atómicos 2D en líquidos
- Nanosilicio para producir hidrógeno
- Nano grafema, memoria transparente flexible basada en silicio
- Efecto superficial sobre el transporte de petróleo en nanocanales:un estudio de dinámica molecular
- Desgaste triboquímico dependiente de la velocidad de deslizamiento del silicio libre de óxido
- Síntesis de compuesto de nanopartículas de oro / nanofibras de sílice conductoras eléctricas mediante pulsos de láser y técnica de pulverización
- Dependencia de la resonancia de plasmón de superficie localizada del dímero de nanoprisma Ag truncado desalineado
- Nanocables de silicio amorfo cultivados en película de óxido de silicio mediante recocido
- Defectos en la superficie del nanofósforo de MgAl2O4 dopado con Ti



