Efecto superficial sobre el transporte de petróleo en nanocanales:un estudio de dinámica molecular

Resumen

En este trabajo, investigamos el mecanismo de dinámica del transporte de petróleo en nanocanales utilizando simulaciones de dinámica molecular. Está demostrado que la interacción entre las moléculas de aceite y el nanocanal tiene un gran efecto sobre las propiedades de transporte del aceite en el nanocanal. Debido a las diferentes interacciones entre las moléculas de aceite y el canal, el desplazamiento del centro de masa (COM) del aceite en un canal de 6 nm es más de 30 veces mayor que el de un canal de 2 nm, y el coeficiente de difusión de las moléculas de aceite en el centro de un canal de 6 nm es casi dos veces más que cerca de la superficie del canal. Además, se encuentra que la polaridad de las moléculas de aceite tiene el efecto de impedir el transporte de aceite, porque la interacción electrostática entre las moléculas de aceite polares y el canal es mucho mayor que la que existe entre las moléculas de aceite no polares y el canal. Además, se encuentra que el componente del canal juega un papel importante en el transporte de petróleo en el nanocanal, por ejemplo, el desplazamiento COM de petróleo en el canal de oro es muy pequeño debido a la gran interacción entre el petróleo y el sustrato de oro. También se ha encontrado que la rugosidad nanométrica de la superficie del canal influye en gran medida en la velocidad y el patrón de flujo del aceite. Nuestros hallazgos contribuirían a revelar el mecanismo de transporte de petróleo en nanocanales y, por lo tanto, son muy importantes para el diseño de la extracción de petróleo en nanocanales.

Antecedentes

Inspirado por la creciente demanda mundial de energía y el consumo excesivo de energía convencional, el desarrollo de petróleo de esquisto no convencional ha ganado una gran atención debido a sus grandes reservas y producción potencial [1]. El aceite de esquisto es la abreviatura de aceite de esquisto orgánico maduro y la energía más representativa que se enumera en los encabezados de energía no convencional. Aunque los recursos totales conocidos de petróleo de esquisto en el mundo son más de tres veces superiores a los del petróleo crudo convencional restante [2], se ha estimado que las reservas explotables totales de petróleo de esquisto son mucho menores que las reservas. Además, la lutita bituminosa se ha explotado durante unos 200 años, pero el desarrollo y la utilización de la lutita bituminosa están muy restringidos hasta ahora. Todo esto sugiere que el petróleo de esquisto, confinado en un nanocanal, es difícil de extraer [3]. El tamaño del canal de la lutita bituminosa varía de 2 a 100 nm de ancho [4, 5], lo que genera una gran área de superficie específica y muchos tipos de efectos de superficie. Bajo la influencia de la interacción de la superficie entre el fluido y el sustrato, pueden surgir muchos fenómenos físicos nuevos, por ejemplo, el agua fluye mucho más rápido dentro de los nanotubos que en un tubo de macroescala clásico [6, 7], se encuentra un aumento anómalo en la capacitancia del carbono en el poro tamaños inferiores a 1 nm [8], la afinidad por el agua en los nanotubos de carbono cambia de hidrófobo a hidrófilo a medida que disminuye el ancho [9]. Al estar ubicado en la lutita bituminosa, con la fuerte interacción superficial entre los fluidos y el sustrato de la lutita, el fluido exhibe muchos caracteres diferentes a los del canal macroscópico, como la distribución de densidad, la mojabilidad y el coeficiente de difusión [10,11,12], resultando en diferentes propiedades de transporte de fluidos a través de dicho nanocanal de aquellos en el canal de macroescala. Usando simulaciones de dinámica molecular (MD), Chen et al. investigaron el comportamiento de transporte del agua dentro de un modelo de nanotubo de carbono y encontraron que el esfuerzo cortante entre el fluido y el canal era sensible al tamaño, y también verificaron las conclusiones de la simulación mediante un experimento en un carbono nanoporoso en glicerina [13]. Xue y col. consideraron el flujo de decano en el nanocanal de sílice bajo la fuerza impulsora de la inundación de gas, y encontraron que la presión inicial y la energía de interacción entre el petróleo y el sustrato desempeñaban un papel importante en el desplazamiento de las gotas de petróleo [14]. Wang y col. simularon el flujo de octano en rendijas de cuarzo mediante simulaciones MD, y encontraron que la velocidad mejoraba con el aumento de la fuerza externa, el ancho del canal y la temperatura, y también encontraron que el efecto de superficie puede dominar el transporte de petróleo en el nanocanal con disminución del ancho del canal [15]. Como se mencionó anteriormente, la fuerte interacción de la superficie entre los fluidos y el nanocanal tiene un efecto crucial en el flujo del fluido en el nanocanal. Sin embargo, hay pocos estudios sistemáticos sobre el efecto de las propiedades de la superficie en el mecanismo dinámico del transporte de petróleo en nanocanales. Comprender la influencia del efecto de la superficie en el transporte de petróleo de esquisto en nanocanales es de gran importancia para promover el desarrollo y la utilización del petróleo de esquisto.

En este trabajo, investigamos el mecanismo dinámico del transporte de petróleo en nanocanales utilizando simulaciones de MD y demostramos que la interacción de la superficie entre las moléculas de aceite y la superficie del canal, la rugosidad de la superficie del canal y la interacción entre las moléculas de aceite tienen grandes efectos en el centro de masa. (COM) desplazamiento de aceite en nanocanal. La conclusión no solo proporcionará un futuro brillante para el campo de la energía, sino que también arrojará luz sobre una amplia gama de ciencias naturales, como el medio ambiente, la biomedicina, la química, la energía y las aplicaciones industriales, incluida la translocación de proteínas, la separación de mezclas por membranas y la batería de canales. [16, 17, 18, 19, 20].

Métodos

Todas las simulaciones de MD se llevan a cabo mediante código Discover en el software Material Studio (Accelrys Inc.). Se utiliza un potencial molecular optimizado en fase condensada para estudios de simulación atomística (COMPASS) para describir las interacciones interatómicas. El campo de fuerza COMPASS es un campo de fuerza general de todos los átomos basado en ab initio y parametrizado utilizando datos extensos para moléculas en la fase condensada. El potencial del campo de fuerza se puede expresar de la siguiente manera:

$$ {E} _ {\ mathrm {total}} ={E} _ {\ mathrm {valencia}} + {E} _ {\ mathrm {cruz} - \ mathrm {término}} + {E} _ {\ mathrm {nonbond}} $$ (1)

En la ecuación anterior, E _valencia se refiere a la energía de valencia (o enlace), que generalmente se explica por términos diagonales como estiramiento del enlace, flexión del ángulo de valencia, torsión del ángulo diedro e inversión. E _{términos cruzados} se refiere a la energía de términos cruzados, que explica factores como las distorsiones de enlaces o ángulos causadas por átomos cercanos para reproducir con precisión las propiedades dinámicas de las moléculas. Y E _{no vinculado} se refiere a la energía no enlazante, que explica las interacciones entre átomos no enlazados y resulta principalmente de las interacciones de van der Waals (vdW) y las interacciones electrostáticas. Los tres términos se pueden representar como

$$ \ begin {array} {c} {E} _ {\ mathrm {valencia}} ={\ displaystyle \ sum_b \ left [{K} _2 {\ left (b- {b} _0 \ right)} ^ 2 + {K} _3 {\ izquierda (b- {b} _0 \ derecha)} ^ 3+ {K} _4 {\ izquierda (b- {b} _0 \ derecha)} ^ 4 \ derecha]} \\ {} \ kern2.5em + {\ displaystyle \ sum _ {\ theta} \ left [{H} _2 {\ left (\ theta - {\ theta} _0 \ right)} ^ 2+ {H} _3 {\ left (\ theta - {\ theta} _0 \ right)} ^ 3+ {H} _4 {\ left (\ theta - {\ theta} _0 \ right)} ^ 4 \ right]} \\ {} \ kern2.5em + {\ Displaystyle \ sum _ {\ phi} \ left [{V} _1 \ left [1- \ cos \ left (\ phi - {\ phi} _1 ^ 0 \ right) \ right] + {V} _2 \ left [1- \ cos \ left (2 \ phi - {\ phi} _2 ^ 0 \ right) \ right] + {V} _3 \ left [1- \ cos \ left (3 \ phi - {\ phi} _3 ^ 0 \ right ) \ derecha] \ derecha]} \\ {} \ kern4.5em + {\ displaystyle \ sum _ {\ chi} {K} _ {\ chi} {\ chi} ^ 2 + {E} _ {\ mathrm {UB }}} \ end {matriz} $$ (2) $$ \ begin {matriz} {l} {E} _ {\ mathrm {cruz} \ hbox {-} \ mathrm {término}} ={\ Displaystyle \ sum_b {\ Displaystyle \ sum_ {b ^ {\ prime}} {F} _ {b {b} ^ {\ prime}} \ left (b- {b} _0 \ right) \ left ({b} ^ {\ prime } - {b} _0 ^ {\ prime} \ right)}} \\ {} + {\ displaystyle \ sum _ {\ theta} {\ displaystyle \ sum _ {\ theta ^ {\ prime}} {F} _ {\ theta {\ theta} ^ {\ prime}} \ left (\ theta - {\ thet a} _0 \ right) \ left ({\ theta} ^ {\ prime} - {\ theta} _0 ^ {\ prime} \ right)}} + {\ displaystyle \ sum_b {\ displaystyle \ sum _ {\ theta} { F} _ {b \ theta} \ left (b- {b} _0 \ right) \ left (\ theta - {\ theta} _0 \ right)}} \\ {} + {\ displaystyle \ sum_b {\ displaystyle \ suma _ {\ phi} {F} _ {b \ phi} \ left (b- {b} _0 \ right) \ times}} \ left [{V} _1 \ cos \ phi + {V} _2 \ cos 2 \ phi + {V} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum_ {b ^ {\ prime}} {\ displaystyle \ sum _ {\ phi} {F} _ {b ^ {\ prime} \ phi} \ left ({b} ^ {\ prime} - {b} _0 ^ {\ prime} \ right) \ left ({b} ^ {\ prime} - {b} _0 ^ {\ prime} \ right) \ times}} \ left [{F} _1 \ cos \ phi + {F} _2 \ cos 2 \ phi + {F} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum _ {\ theta} {\ displaystyle \ sum _ {\ phi} {F} _ {\ theta \ phi} \ left (\ theta - {\ theta} _0 \ right) \ times}} \ left [{V} _1 \ cos \ phi + {V} _2 \ cos 2 \ phi + {V} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum _ {\ phi} {\ displaystyle \ sum _ {\ theta} { \ Displaystyle \ sum _ {\ theta ^ {\ prime}} {K} _ {\ phi \ theta {\ theta} ^ {\ prime}} \ cos \ phi \ left (\ theta - {\ theta} _0 \ right) \ times \ left ({\ theta} ^ {\ prime} - {\ theta} _0 ^ {\ prime} \ right)}}} \ end {matriz} $$ (3) $$ {E} _ {\ mathrm {non} \ hbox {-} \ mathrm {bond}} ={\ displaystyle \ sum_ {i> j} \ left [\ frac { A_ {ij}} {r_ {ij} ^ 9} - \ frac {B_ {ij}} {r_ {ij} ^ 9} \ right]} + {\ displaystyle \ sum_ {i> j} \ frac {q_i { q} _j} {\ varepsilon {r} _ {ij}}} + {E} _ {\ mathrm {H} \ hbox {-} \ mathrm {enlace}} $$ (4)

donde b y b ′ Son las longitudes de enlace de dos enlaces adyacentes, y θ , ϕ y χ son el ángulo de dos enlaces, el ángulo de torsión diedro y el ángulo fuera del plano, respectivamente. q es la carga atómica, ε es la constante dieléctrica, r _ij es el i - j distancia de separación atómica. b ₀ , K _i ( yo =2 - 4), θ ₀ , H _i ( yo =2 - 4), \ ({\ phi} _i ^ 0 \) ( i =1-3), V _i ( yo =1-3), \ ({F} _ {b {b} ^ {\ prime}} \), \ ({b} _0 ^ {\ prime} \), \ ({F} _ {\ theta { \ theta} ^ {\ prime}} \), \ ({\ theta} _0 ^ {\ prime} \), F _bθ , F _bϕ , \ ({F} _ {b ^ {\ prime} \ theta} \), F _i ( yo =1-3), F _θϕ , \ ({K} _ {\ phi \ theta {\ theta} ^ {\ prime}} \), A _ij y B _ij se ajustan a partir de cálculos de mecánica cuántica y se implementan en el módulo Discover de Materials Studio. El potencial de Lennard-Jones se emplea para describir interacciones intermoleculares entre moléculas de aceite, moléculas de aceite y nanocanales [14, 21, 22]. La distancia de corte de 15,5 Å se selecciona para calcular las interacciones vdW, y el método de Ewald y el método basado en átomos se aplican para el cálculo de las interacciones electrostáticas y las interacciones vdW, respectivamente. El sistema se calcula a volumen y temperatura constantes, es decir, se emplea el conjunto NVT. La temperatura es de 298 K y se elige el método del termostato Andersen para controlar el sistema a una temperatura termodinámica. La condición de frontera periódica se impone en las tres dimensiones. Los datos se recopilan cada 5 ps y se registra la trayectoria completa y precisa.

Una composición importante de minerales de roca es la sílice en la mayoría de las formaciones de esquisto [23,24,25]. Entonces, la superficie de sílice se selecciona como superficie de pizarra bituminosa en nuestra simulación. El entramado inicial de sílice proviene de la base de datos del software Material Studio. La superficie (0 0 1) se corta y luego se refina una superficie rectangular. Las dimensiones de la superficie de cada sustrato son 1,5 × 7 × 0,85 nm ³ . Un canal de separación a lo largo de la z Se crea un eje entre las dos superficies del sustrato como se muestra en la Fig. 1a. Las superficies de los canales están completamente modificadas por hidroxilo para representar las condiciones geológicas [26].

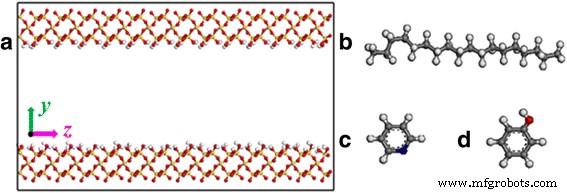
un Representación del modelo de nanocanal de sílice. Estructuras moleculares de b octadecano, c piridina y d fenol. Código de color para átomos: rojo , oxígeno; blanco , hidrógeno; amarillo , silicio; gris , carbono; y azul , nitrógeno

La configuración inicial del sistema está construida por moléculas de octadecano empaquetadas dentro del canal de sílice. Se insertan cuarenta moléculas de octadecano en el canal de la hendidura con un ancho de 2 nm, lo que da como resultado una densidad de 0,8 g / cm ³ . También estudiamos las propiedades de transporte de las moléculas de piridina y fenol, otros dos componentes del aceite de esquisto, para investigar el efecto de las moléculas de aceite en el transporte de aceite en nanocanales. Las estructuras de octadecano, piridina y fenol se extraen de la base de datos del software Material Studio, como se muestra en la Fig. 1b – d. Para asegurar una densidad similar de aceite, el número de moléculas de piridina, moléculas de fenol y moléculas de octadecano en canales con anchos de 4 y 6 nm en nuestras simulaciones es 407, 344, 80 y 120, respectivamente.

Al utilizar Discover Minimization, primero realizamos la minimización de energía para optimizar el sistema de modo que el sistema esté bien equilibrado. Las simulaciones de equilibrio se realizan utilizando un prerun de 500 ps para garantizar que el sistema haya alcanzado un estado estable. Luego, se realizan simulaciones de no equilibrio aplicando una fuerza similar a la gravedad paralela a la superficie del canal (a lo largo de la z -eje) a todas las moléculas de aceite con el fin de promover el transporte a través de canales, que se utiliza comúnmente en la simulación del transporte de fluidos [27,28,29]. Observamos aquí que una limitación de la simulación de MD es que una fuerza comparable a la de los entornos ambientales no es práctica, debido al tiempo requerido para los cálculos de MD; por lo tanto, aplicamos una fuerza que arroja un valor promedio de 3,1 × 10 ⁻¹⁴ N en cada átomo. La intención de la fuerza grande es obtener datos más precisos para el transporte de petróleo dado un tiempo de simulación finito.

Resultados y discusión

Efecto del ancho del canal

En primer lugar, prestamos atención al efecto del ancho del canal en las propiedades de transporte del petróleo. Bajo la acción de la fuerza externa, el número de átomos que fluyen a través de la sección transversal del canal aumenta gradualmente con el tiempo de simulación (Archivo adicional 1:Figura S1, Información complementaria). Las moléculas de aceite se extraen durante aproximadamente 2 ns. Como se muestra en la Fig. 2d-f, con el incremento del ancho del canal, la distancia de desplazamiento del petróleo es mayor después de simulaciones MD de 2 ns. Para describir cuantitativamente el desplazamiento del petróleo a lo largo del eje del canal, calculamos el desplazamiento COM del petróleo entre su ubicación inicial y su ubicación final después de 2 ns. Simulaciones de MD y su ubicación inicial a lo largo de la z El eje y el centro de masa se definen en términos de un promedio ponderado de masa de las coordenadas del átomo.

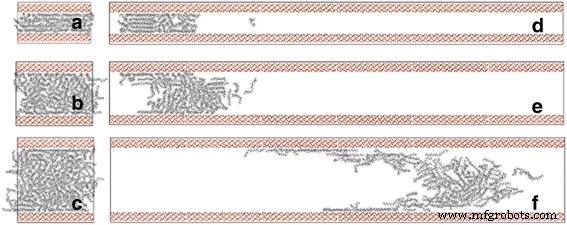
El modelo inicial del proceso de transporte de moléculas de octadecano impulsado por la fuerza en canales de sílice con anchos de a 2, b 4 y c 6 nm e instantáneas de moléculas de octadecano en d 2, e 4 y f Canales de 6 nm a 2 ns

$$ {z} _ {\ mathrm {COM}} ={\ Displaystyle \ sum_i \ frac {m_i} {M} {r} _i} $$ (5)

En la Fig. 3, presentamos el desplazamiento de aceite después de simulaciones MD de 2 ns. Los resultados muestran que bajo la condición de la misma fuerza de tracción en cada átomo, el desplazamiento COM del aceite en el canal de 2 nm es solo de 0,85 nm, que es mucho más pequeño que en el canal de 6 nm. Sugiere que el canal más estrecho proporciona una restricción de adsorción más pronunciada en las moléculas de aceite.

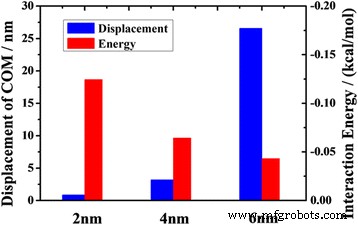
Los desplazamientos COM del petróleo a 2 ns y las energías de interacción promedio entre el petróleo y el canal frente al ancho del canal

Para aclarar el efecto de la restricción de adsorción, calculamos la energía de interacción promedio entre las moléculas de aceite y el sustrato. La energía de interacción promedio se calcula de la siguiente manera:

$$ {E} _ {\ mathrm {promedio} \ \ mathrm {interacción}} =\ frac {E _ {\ mathrm {total}} - \ left ({E} _ {\ mathrm {aceite}} + {E} _ {\ mathrm {sustrato}} \ right)} {N} $$ (6)

donde E _{interacción promedio} es la energía de interacción promedio entre la molécula de aceite y el sustrato; E _total representa la energía total de todo el sistema; E _aceite y E _sustrato son la energía de los componentes del aceite y los componentes del sustrato, respectivamente; y N es el número total de átomos de moléculas de aceite [14, 30, 31]. La Figura 3 muestra que el desplazamiento de aceite disminuye con el aumento de la energía de interacción promedio. Es obvio que la adsorción entre las moléculas de aceite y el canal crece con la energía de interacción. La fuerte adsorción del canal inhibe el transporte de aceite en un canal estrecho. A partir de los datos ilustrados en la Fig. 3, encontramos que cuando la energía de interacción aumenta tres veces, el desplazamiento de aceite disminuye en más de 30 veces. Sugiere que el transporte de aceite está muy influenciado por la interacción entre la molécula de aceite y el sustrato. Sin embargo, este efecto disminuye al aumentar el ancho del canal. El efecto de tamaño en el transporte de petróleo es más obvio en el nanocanal que en el microcanal (archivo adicional 1:Figura S2). Por lo tanto, la reducción de la energía de interacción entre la molécula de aceite y el sustrato es un factor clave para mejorar el transporte de aceite en el nanocanal.

Puede verse en la Fig. 2 que ha habido estructuras de capas obvias cerca de la superficie del nanocanal, con un grosor de aproximadamente 5 Å. Cabe señalar que la capa que contacta con la superficie del canal y la capa en el centro del canal se denominan capa de contacto y capa central, respectivamente. Obviamente, las capas de moléculas de aceite bien ordenadas se encuentran en la región cercana a la superficie. La orientación de las moléculas de octadecano se caracteriza comúnmente por el ángulo θ entre el vector normal a la superficie del canal y algunos vectores que están formados por la línea que conecta los dos átomos de carbono al final de una molécula de octadecano [15, 29]. La distribución de la orientación para las moléculas de octadecano en cada capa a 2 ns se presenta en la Fig. 4. Aquí, θ =80 ^o ∼ 90 ^o corresponde a la orientación paralela de la molécula, mientras que un valor de θ =0 ^o ∼ 10 ^o significa que la molécula es perpendicular a la superficie del canal. Se puede ver que las moléculas de octadecano son principalmente paralelas a la superficie en capas de canal de 2 nm y en la capa de contacto de canal de 4 nm y canal de 6 nm, debido a la fuerte interacción aceite-superficie (Fig. 5b). Para las capas centrales del canal de 4 nm y el canal de 6 nm, no existe una orientación preferencial de las moléculas de octadecano, lo que significa que esas moléculas de octadecano tienden a ubicarse en varios ángulos con respecto a la superficie del canal. Las moléculas de octadecano alineadas en la capa de contacto pueden ser importantes para las propiedades de transporte de las moléculas de aceite en el nanocanal.

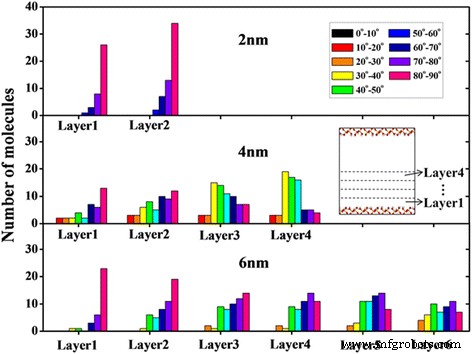
La distribución del ángulo de orientación de las moléculas de octadecano en cada capa para diferentes anchos de canal

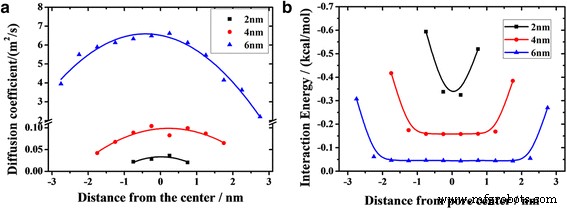
un Perfiles de coeficiente de difusión de aceite en canales de diferente ancho. b Dependencia de la distancia de la energía de interacción promedio entre moléculas de aceite y sílice (con símbolos). Las líneas continuas representan las funciones de ajuste

A continuación, observamos que los tiempos de inicio (definidos como el tiempo en el que el desplazamiento de una capa es superior a 5 Å) para varias capas son diferentes al comprobar las trayectorias. Los datos de tiempo de inicio enumerados en la información de apoyo (archivo adicional 1:Tabla S1) muestran que el tiempo de inicio de la capa de contacto aumenta con la disminución del ancho del canal, lo que significa que la fuerza de tracción necesaria para iniciar el movimiento de una capa de contacto en un canal más estrecho es más grande que el requerido en un canal más ancho. Además, el tiempo de inicio de la capa central es mucho antes que el de la capa de contacto.

Además, encontramos que la tasa de flujo de petróleo disminuye al aumentar la distancia desde el eje del canal, y la tasa de flujo de la capa de contacto disminuye al disminuir el ancho del canal (Fig. 2d-f). Para describir cuantitativamente estos caracteres, estudiamos el coeficiente de difusión de las moléculas de aceite en una ubicación diferente lejos del centro del canal, que se obtiene de la evolución en el tiempo del desplazamiento cuadrático medio según

$$ D =\ frac {1} {4} \ underset {t \ to \ infty} {\ lim} \ frac {\ mathrm {d}} {\ mathrm {d} t} \ left \ langle {\ left | {r} _i (t) - {r} _i (0) \ right |} ^ 2 \ right \ rangle $$ (7)

donde r _i denota el vector de posición de i th partícula, y los corchetes angulares denotan un promedio de conjunto. La Figura 5a muestra cómo los coeficientes de difusión de las capas dependen de la posición en el nanocanal. Las curvas del canal de 4 nm y del canal de 6 nm presentan un estilo de parábola, es decir, hacia la superficie del canal, los coeficientes de difusión de las capas disminuyen gradualmente. El canal de 6 nm muestra la mayor diferencia entre el valor alto y el valor bajo de 4,4 m ² / s, mientras que el canal de 2 nm mantiene la diferencia mínima de 0,016 m ² /s. Los coeficientes de difusión de las capas en el canal de 2 nm son ligeramente diferentes, por lo que la superficie frontal del aceite parece un pistón. Además, encontramos que los coeficientes de difusión de las capas a la misma distancia de la superficie del canal son bastante diferentes para varios canales (Fig. 5a). Por ejemplo, el coeficiente de difusión de la capa que entra en contacto con la superficie del canal inferior en un canal de 6 nm es de 3,9 m ² / s, mientras que en el canal de 2 nm es solo 0.02 m ² /s. Significa que la velocidad de flujo de las capas a la misma distancia de la superficie del canal aumenta al aumentar el ancho del canal.

En la Fig. 5b, presentamos la energía de interacción promedio entre las moléculas de aceite en diferentes ubicaciones lejos del centro del canal y el canal. Las energías de interacción son obviamente mayores en ambos extremos de las curvas y disminuyen rápidamente dentro de 1 nm ya que el sustrato tiene una fuerte adsorción en moléculas de aceite en el rango de 1 nm, y es una de las razones del lento inicio de las capas de contacto. Sin embargo, las energías de interacción entre las moléculas de aceite y el canal no pueden explicar adecuadamente la forma de la superficie frontal, ya que sus valores para las capas fuera del rango de adsorción fuerte son casi los mismos. La superficie frontal de la parábola no solo está relacionada con la interacción entre el aceite y el canal, sino también con la interacción entre las moléculas de aceite. La interacción intermolecular contribuye a la viscosidad del fluido, que juega un papel importante en la transferencia de impulso en el fluido viscoelástico. Dado que el rango de adsorción del canal en el aceite es de aproximadamente 1 nm, algunas capas están ubicadas en el área, como están marcadas por la sombra en la Fig. 6. Las fuertes interacciones superficiales entre el aceite y el sustrato bloquean el transporte de las capas de aceite en la sombra. El impulso se transfiere de las capas fuera de la sombra a las capas en la sombra. El número de átomos fuera de la sombra disminuye al disminuir el ancho del canal. Por lo tanto, se transfiere menos impulso a las capas en sombra en un canal más estrecho. Entonces, la velocidad de difusión de la capa de contacto disminuye al disminuir el ancho del canal.

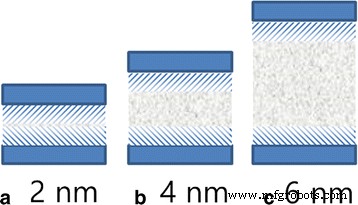
un , b , c Esquema del rango de adsorción entre aceite y sustrato

Efecto de la polaridad

El aceite de esquisto siempre contiene los componentes del aceite polar, y estos componentes del aceite polar juegan un papel importante en la adsorción de la interfaz aceite / sílice [21, 32], por lo que comprender su impacto en el transporte de petróleo es de vital importancia. Con fenol y piridina, por ejemplo, realizamos simulaciones en un canal de 4 nm, y los números de átomos de fenol y piridina son aproximadamente iguales al número de átomos de octadecano en el canal de 4 nm. Las instantáneas de piridina, fenol y octadecano en el canal de sílice a 2 ns se muestran en la Fig. 7. En comparación con las moléculas de octadecano, las moléculas de fenol y piridina casi no pueden ser impulsadas por la fuerza de tracción. La línea discontinua en la Fig. 8 muestra los desplazamientos COM de diferentes moléculas de aceite después de simulaciones MD de 2 ns. Aunque las fuerzas de tracción en cada átomo son iguales, el desplazamiento COM del octadecano es casi 16 veces mayor que el desplazamiento COM del fenol y la piridina.

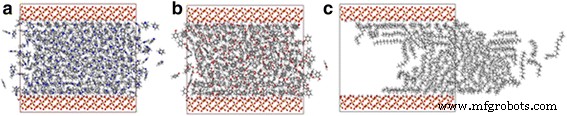
Instantáneas de a piridina, b fenol y c transporte de octadecano en canales de sílice de 4 nm a 2 ns

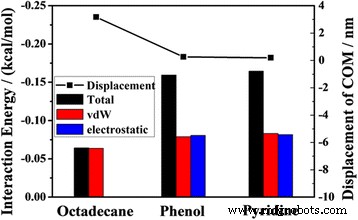
Los desplazamientos COM del aceite a 2 ns y las energías de interacción promedio (total, vdW y electrostática) entre los diferentes componentes y el canal

Para comprender estos resultados, calculamos la energía de la interacción total, la interacción vdW y la interacción electrostática entre los diferentes componentes y el canal. El histograma de la Fig. 8 ilustra que la energía de interacción total entre el fenol (piridina) y el sustrato de sílice es mayor que entre el octadecano y el canal de sílice. Debido a que la molécula de octadecano es una molécula no polar en cadena, la interacción total entre las moléculas de octadecano y el canal resulta principalmente de la interacción vdW, y hay poca interacción electrostática, mientras que las contribuciones de la interacción vdW y la interacción electrostática entre fenol (piridina) y el canal hacia la interacción total es casi el mismo.

Para investigar la influencia de la polaridad en el transporte de petróleo, calculamos el momento dipolar de las tres moléculas usando la simulación del primer principio. Los detalles de la actuación siguen nuestro trabajo anterior [33,34,35,36]. Los resultados muestran que los momentos dipolares de octadecano, fenol y piridina son 0.0322, 1.3059 y 2.2449 Debye, respectivamente. Indica que las moléculas de aceite polares son mucho más difíciles de manejar que las moléculas no polares en el nanocanal. Pero el desplazamiento COM del aceite no siempre aumenta con la polaridad decreciente. Para las dos moléculas de aceite polares, la polaridad del fenol es más débil que la polaridad de la piridina, pero sus desplazamientos COM son casi iguales.

Efecto de los tipos de materiales

Los caracteres de transporte de las moléculas de aceite también se comparan entre esos nanocanales fabricados a partir de varios tipos de materiales, incluidos sílice, oro y calcita. La Figura 9 muestra las instantáneas de moléculas de octadecano en canales de calcita y oro a 2 ns. La Figura 9a muestra un transporte distinto de moléculas de aceite en el canal de calcita, lo que indica que las moléculas de octadecano en la calcita también pueden ser impulsadas por la fuerza de tracción, mientras que las moléculas en el canal de oro apenas pueden moverse (Fig. 9b).

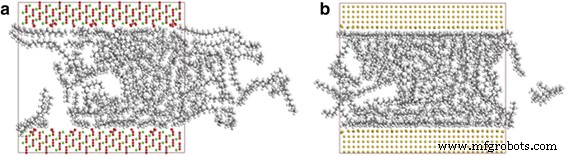
Instantáneas del transporte de octadecano en 4 nm a canal de calcita y b canal de oro a 2 ns. Código de colores para átomos:verde, calcio; amarillo, dorado

La Figura 10 muestra los desplazamientos COM de moléculas de octadecano en canales de varios materiales y las energías de interacción promedio entre el aceite y los diferentes canales de materiales. El desplazamiento COM de aceite en el canal de sílice es mucho mayor que en el canal de oro. El fenómeno puede explicarse por el efecto de la interacción entre las moléculas de aceite y el canal. La interacción promedio es mucho menor entre las moléculas de aceite y el canal de sílice que entre las moléculas de aceite y el canal de oro. Pero para el transporte de las moléculas de aceite en el canal de sílice y en el canal de calcita, este factor no puede explicar adecuadamente la diferencia. La energía de interacción promedio entre las moléculas de aceite y el canal de sílice no parece ser muy diferente de la que existe entre las moléculas de aceite y el canal de calcita, pero los desplazamientos de COM en los dos casos son bastante diferentes. La razón puede estar correlacionada con los átomos de la superficie y la textura de la superficie. Estos resultados indican que el transporte de petróleo está muy influenciado por la interacción entre las moléculas de petróleo y el canal, pero cuando los valores de la energía de interacción son similares, el transporte de petróleo en nanocanal es la competencia entre esos factores.

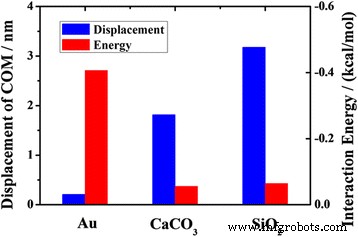
Los desplazamientos COM del aceite a 2 ns y las energías de interacción promedio entre el aceite y sustratos de diferentes materiales

Efecto de la rugosidad de la superficie

Como es bien sabido, la rugosidad de la superficie de tamaño nanométrico tiene poca influencia en los flujos de fluido dentro de los canales de tamaño micro. Sin embargo, se ha demostrado que la rugosidad de la superficie de tamaño nanométrico tiene una gran influencia en el transporte de fluidos en los nanocanales [37,38,39]. Para investigar el efecto de la rugosidad en el transporte de octadecano, construimos superficies rugosas cortando una pequeña cantidad de átomos de la superficie del sustrato, de modo que una cavidad con una profundidad de d =3 Å (o 6 Å) y se forma un ancho de 35 Å en la superficie del sustrato. Los átomos desnudos de oxígeno fueron modificados por átomos de hidrógeno. Five and ten octadecane molecules are added to 3 Å cavity and 6 Å cavity, respectively, and the external force is increased correspondingly. Figure 11 shows the comparison of snapshots for octadecane flowing through rough channel with cavity depths of 3 and 6 Å at 2 ns. We observe that inside every cavity, there are some oil molecules, and their localizations are affected by the cavity, which results in a reduction of velocity values inside the cavity, as well as the velocity of oil molecules nearby. And this becomes more obvious when d = 6 Å, as shown in Fig. 11b. To quantify the influence of roughness on transportation, we further calculate the COM displacement of oil in rough channels. The COM displacements of oil in channels with 3 and 6 Å depth cavity are 3.95 and 3.07 Å, respectively. When d = 6 Å, the value of oil displacement is 3.07 Å, which is smaller than the value 3.17 Å of oil molecules in flat channel. Somewhat surprisingly, however, for d = 3 Å, the displacement is even larger than that in flat channel. We expect that these characters are contributed by two parts:(1) the cavity increases the width of the nanochannel so that the oil molecules have a greater diffusion coefficient according to the above discussion, which facilitates the transportation of oil; (2) the oil molecules in cavity can suppress the transportation of oil molecules nearby and therefore decrease the oil transportation speed. For the oil molecules in channel with d = 3 Å, the effect of suppression caused by the less oil molecules in cavity is less than the effect of facilitation caused by the width increment. When d = 6 Å, the diffusion coefficient of oil molecules is further increased; however, more oil molecules are suppressed by the deeper cavity, and the effect of suppression on the transportation of oil molecules is more than that of facilitation, thereby reducing the oil displacement. Because of these complications, we cannot separate these parts and judge how much contribution of each part has on the displacement.

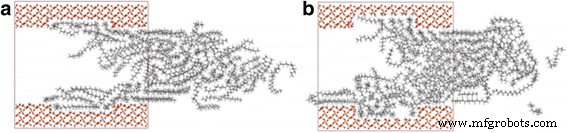
Snapshots of octadecane transportation in rough channel with the cavity depth of a 3 and b 6 Å at 2 ns

Conclusions

In this study, we investigate the mechanism of oil transportation in nanochannels using molecular dynamics simulations. It is demonstrated that the oil displacement in a 6 nm channel is over 30 times larger than that in a 2 nm channel, and the diffusion coefficient of oil molecules at the center of the 6 nm channel is almost two times more than that near the channel surface, due to interaction difference between the oil molecules and channels. Besides, we find that both the polarity of oil molecules and channel component have great effects on the interaction between oil molecules and channel in the channels with same width; the larger the interaction between oil molecules and channel is, the smaller the oil displacement is. Finally, we demonstrate that surface roughness can obviously affect oil transportation in nanochannels. The mechanism by which the cavity structure affects the transportation of oil is an intricate issue, which should be further studied. Our findings would contribute to revealing the mechanism of oil transportation in nanochannels and therefore are very important for design of oil extraction in nanochannels.

Abreviaturas

COM:: Center of mass
COMPASS:: Condensed-phase optimized molecular potential for atomistic simulation studies
MD:: Molecular dynamics
vdW:: van der Waals

Las nanotecnologías desactivan las células madre cancerosas NiCo2S4 @ NiMoO4 Arreglos de nanotubos de heteroestructura de núcleo-carcasa cultivados en espuma de Ni como un electrodo libre de aglutinantes que muestran un alto rendimiento electroquímico con al…

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias