Dependencias de temperatura y presión de las propiedades elásticas de los cristales individuales de tantalio bajo una carga de tracción <100>:un estudio de dinámica molecular
Resumen
Las simulaciones atomísticas son capaces de proporcionar información sobre los mecanismos físicos responsables de las propiedades mecánicas del metal de transición del tantalio (Ta). Utilizando el método de dinámica molecular (MD), se investigan las dependencias de temperatura y presión de las propiedades elásticas de los monocristales de Ta mediante una carga de tracción <100>. En primer lugar, se realiza un estudio comparativo entre dos tipos de potenciales del método del átomo incrustado (EAM) en términos de las propiedades elásticas de los monocristales de Ta. Los resultados muestran que el potencial de Ravelo-EAM (Physical Review B, 2013, 88:134101) se comporta bien a diferentes presiones hidrostáticas. Luego, los resultados de la simulación MD basados en el potencial Ravelo-EAM muestran que Ta experimentará una transición de fase cúbica centrada en el cuerpo (BCC) a cúbica centrada en la cara (FCC) antes de la fractura bajo una carga de tracción <100> a una temperatura de 1 K , y el tamaño del modelo y la velocidad de deformación no tienen efectos obvios sobre los comportamientos de tracción de Ta. A continuación, a partir de los resultados de la simulación a la temperatura del sistema de 1 a 1500 K, se puede derivar que el módulo elástico de E 100 Disminuye linealmente con el aumento de temperatura, mientras que la tensión de fluencia disminuye con la conformación de una fórmula polinomial cuadrática. Finalmente, la dependencia de la presión de las propiedades elásticas se realiza de 0 a 140 GPa y las observaciones muestran que el módulo elástico aumenta con el aumento de la presión en general.
Antecedentes
En general, el tantalio (Ta) pertenece a la estructura BCC en condiciones ambientales. En la actualidad, numerosas publicaciones han demostrado que los monocristales de Ta muestran una excelente estabilidad de fase [1, 2, 3] a altas presiones. Además, Ta tiene una temperatura de fusión muy alta de 3269 K a presión ambiente, que es más alta que la mayoría de los otros metales [4]. Debido a sus excelentes propiedades, el Ta es un material ideal para muchas aplicaciones tecnológicas, como barrera de difusión en micro / nanoelectrónica, recubrimiento de protección contra el desgaste y superaleaciones de alta temperatura.
Recientemente, se ha realizado un gran esfuerzo tanto en campos experimentales [2, 5,6,7] como teóricos [8,9,10,11,12,13,14] en las propiedades de alta presión y alta temperatura de Ejército de reserva. Dewaele y col. [5] estudiaron los efectos de la presión sobre el límite elástico de Ta en una celda de yunque de diamante (DAC) hasta 93 GPa, y los experimentos DAC también presentaron que la estructura BCC se mantuvo estable hasta 135 GPa [2]. Además, Shigeaki [8] simuló la ecuación de estado (EOS) de Ta hasta 100 GPa y 3000 K usando DFT. Wu y col. [9] investigó las propiedades elásticas y termodinámicas de Ta a altas presiones de hasta 350 GPa. Mientras tanto, Škoro et al. [6, 7] midieron el límite elástico y el módulo de Young de Ta a temperaturas muy altas de hasta 2250 y 2500 K, respectivamente. Gu y col. [10] realizó un estudio sobre la estructura de alta presión y las propiedades elásticas del Ta cúbico hasta 500 GPa utilizando el método de los primeros principios. Se encuentra que las constantes elásticas en función de la presión, y que el volumen, el módulo de Young y el módulo de corte de Ta aumentaron con el aumento de la presión.
Además de los experimentos de DAC y los cálculos de DFT, también hay muchos estudios a alta temperatura y alta presión en el campo de las simulaciones de MD [15,16,17,18]. Liu y col. [15] utilizó el potencial extendido de Finnis-Sinclair (EFS) e investigó el EOS térmico, así como las propiedades de fusión del Ta a presiones de hasta 400 GPa. Además, Tramontina et al. [16, 17] estudiaron los efectos de la orientación de los cristales sobre los mecanismos de plasticidad a altas presiones. También discutieron la influencia de la fuerza del impacto y el tiempo de aumento del impacto en sus microestructuras. Además, Ruestes et al. [18] llevó a cabo simulaciones de indentación para BCC Ta utilizando tres potenciales interatómicos diferentes y presentó los mecanismos de defectos responsables de la creación y expansión de la zona de deformación plástica.
A pesar de las numerosas investigaciones anteriores, no ha habido un estudio de simulación atomística sistemática de la respuesta dinámica de Ta bajo carga de tracción utilizando simulaciones MD. El objetivo principal del presente trabajo es investigar las propiedades elásticas de los monocristales de Ta bajo una carga de tracción <100>, considerando los efectos del tamaño, la velocidad de deformación, la temperatura y la presión. Además, comprender si se podría inducir una transición de fase a través de <100> cargas de tracción es otro propósito de este trabajo.
Métodos / Experimental
Modelado físico
Como se muestra en la Fig.1, la Ta cúbica investigada en este documento se genera repitiendo una celda unitaria BCC a lo largo de las orientaciones <001>, <010> y <100> y los parámetros de la red son a = b = c =3.301 Å, respectivamente. Cuatro modelos cúbicos con diferentes longitudes de borde, que incluyen 12 a (3,96 nm), 18 a (5,94 nm), 24 a (7,92 nm) y 30 a (9,90 nm), están construidos. El número correspondiente de átomos es 3456, 11,664, 27,648 y 54,000, respectivamente. La Figura 1 muestra el mapa esquemático de Ta cúbico con una longitud de borde de 3,96 nm, que es la estructura original en nuestras simulaciones actuales.
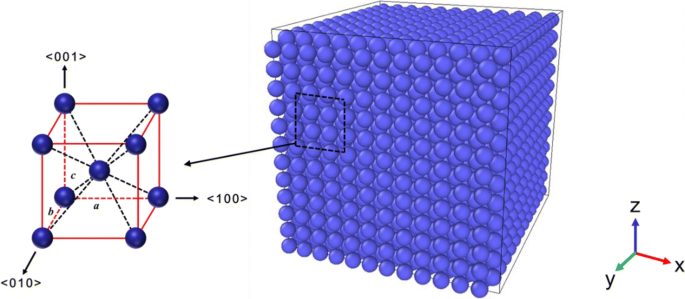
Estructura de BCC y croquis de la Ta cúbica con una longitud de borde de 3,96 nm. El croquis es la estructura original en nuestras simulaciones actuales
Detalles de la simulación de MD
Nuestras simulaciones MD descritas en este artículo se realizan utilizando el simulador atómico / molecular masivamente paralelo a gran escala (LAMMPS) [19]. Durante el proceso de simulación MD, la fuerza externa aplicada sobre los átomos de Ta se calcula de acuerdo con las funciones de potencial interatómico entre esos átomos. En este estudio, se consideran dos potenciales interatómicos diferentes:el potencial EAM de Zhou et al. [20] y Ravelo et al. [21], respectivamente. Ambos potenciales se aplicaron para reproducir algunas propiedades elásticas de Ta que se enumeran en la Tabla 1. En aras de la simplicidad, se denominarán potenciales Ravelo-EAM y Zhou-EAM.
El comportamiento elástico de estructuras con simetría cúbica se describe completamente por sus constantes elásticas, C 11 , C 12 y C 44 . El módulo de elasticidad dependiente de la orientación para los monocristales <100>, <110> y <111> se calcula mediante las diversas ecuaciones [18]. En nuestro trabajo, se realizan simulaciones MD para estudiar los efectos sobre el módulo elástico bajo una carga de tracción <100>. Por lo tanto, nos enfocamos en el módulo elástico para la orientación <100> y tomamos el módulo elástico de E 100 en cuenta. En consecuencia, consideramos las constantes elásticas C 11 y C 12 así como la siguiente ecuación [22]:
$$ {E} _ {100} =\ frac {\ left ({C} _ {11} - {C} _ {12} \ right) \ left ({C} _ {11} +2 {C} _ {12} \ right)} {\ left ({C} _ {11} + {C} _ {12} \ right)} $$ (1)En general, existen tres métodos para calcular las constantes elásticas de MD, incluido el método de fluctuación de tensión, el método de fluctuación de deformación y el método directo. En el presente trabajo, el método directo que es similar al de Gao et al. [23] se utiliza para calcular las constantes elásticas C 11 y C 12 para dos tipos de potenciales EAM, como se muestra en la Fig. 2.
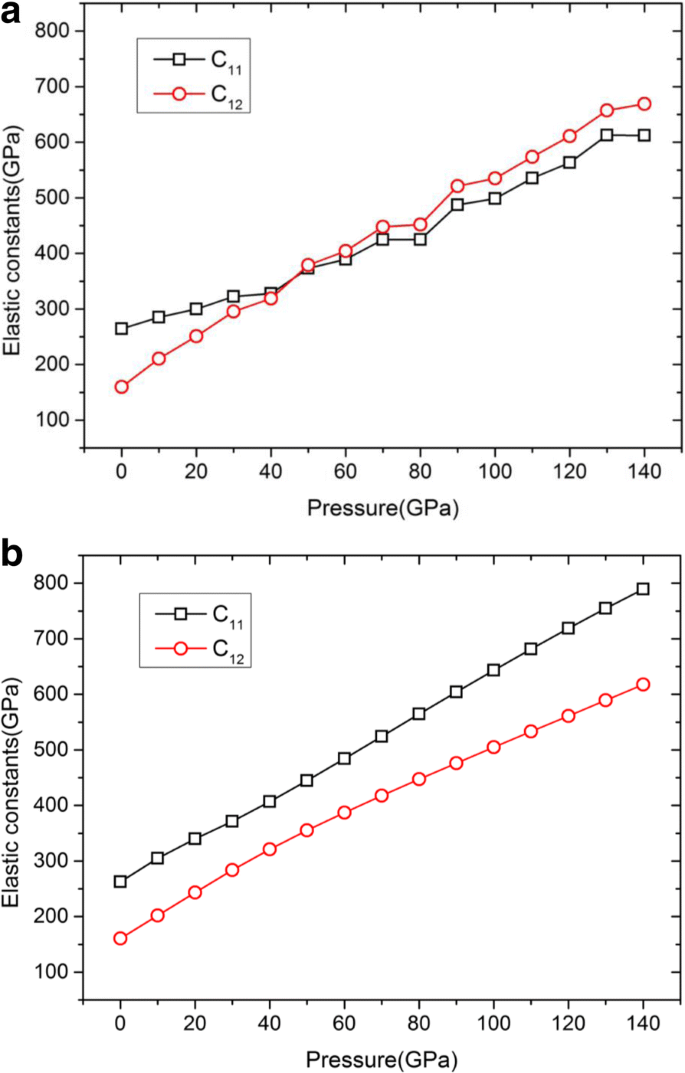
Dependencia de la presión de las constantes elásticas de C 11 y C 12 basado en los potenciales estudiados. un Zhou-EAM. b Ravelo-EAM. En el presente trabajo, utilizamos el método directo para calcular las constantes elásticas C 11 y C 12 para dos tipos de potenciales EAM. Las curvas de presión C11 / C12 para dos potenciales se muestran en a y b , respectivamente
De la Fig. 2a, se puede encontrar que las curvas obtenidas de ambos C 11 y C 12 basado en el potencial de Zhou-EAM no puede seguir funcionando sin problemas con el aumento de presión hasta 140 GPa. Hay un punto de cruce a la presión de ~ 40 GPa, es decir, C 11 = C 12 , en el que el módulo elástico de E 100 será cero según Eq. (1). Además, E 100 Presentará un valor negativo la presión superior a 40 GPa, lo que es sospechoso y contradice los resultados teóricos y experimentales [24, 25]. Por lo tanto, el potencial de Zhou-EAM se desempeña mal en el rango considerado aquí. Luego, examinemos la viabilidad del potencial Ravelo-EAM a partir de los resultados de la simulación MD de C 11 y C 12 basado en el potencial Ravelo-EAM ilustrado en la Fig. 2b. Los resultados numéricos muestran que cuanto mayor es la presión, mayores son los valores de C 11 y C 12 , que concuerda bien con la tendencia de las constantes elásticas que cambian con las presiones a través de los cálculos de DFT [9, 25]. Mientras tanto, los resultados calculados utilizando el potencial Ravelo-EAM son notables al igual que los valores reportados por Ruestes et al. [18]. El potencial Ravelo-EAM se comporta bien a alta presión y al mismo tiempo también puede describir las propiedades elásticas y mecánicas de Ta bajo deformación dinámica [26]. Por lo tanto, realizaremos nuestras simulaciones basadas en el potencial Ravelo-EAM en las siguientes secciones.
Después de la construcción geométrica, llevamos a cabo una serie de simulaciones MD relevantes. Durante las simulaciones MD, las condiciones de contorno periódicas (PBC) se utilizan en las tres direcciones de los modelos cúbicos. El paso de tiempo se establece en 1 fs y la temperatura del sistema se establece en 1, 300, 600, 900, 1200 y 1500 K para explorar la dependencia de la temperatura de las propiedades elásticas de Ta. Primero, el modelo se relaja en un proceso de relajación de 50 ps utilizando una simulación de MD de conjunto canónico (NVT) para que el sistema se encuentre en el mínimo de potencial local. Luego, usó simulación MD isotérmica-isobárica (NPT) para asegurar una presión hidrostática especificada en el rango de 0 a 140 GPa para estudiar los efectos de la presión sobre las propiedades elásticas de Ta [27]. Finalmente, una carga de tracción con una tasa de deformación que varía de 5 × 10 8 s - 1 hasta 7,5 × 10 9 s - 1 [28, 29] se aplica en la dirección x de Ta cúbica. Mientras tanto, la simulación NPT se realiza en las direcciones y y z a la misma presión aplicada en el segundo paso. Por lo tanto, el módulo elástico calculado aquí es para la orientación <100>. Para todas las simulaciones de MD, los modelos se estirarán hasta un alargamiento del 15% en la dirección x a través de <100> carga de tracción.
Resultados y discusión
Proceso de estiramiento
Durante el proceso de estiramiento, las configuraciones simuladas se visualizan utilizando el paquete de software científico Open Visualization Tool (OVITO) [30]. La curva tensión-deformación de Ta bajo <100> deformaciones uniaxiales de tracción a presión cero y las correspondientes configuraciones atómicas con diferentes deformaciones se muestran en la Fig. 3.
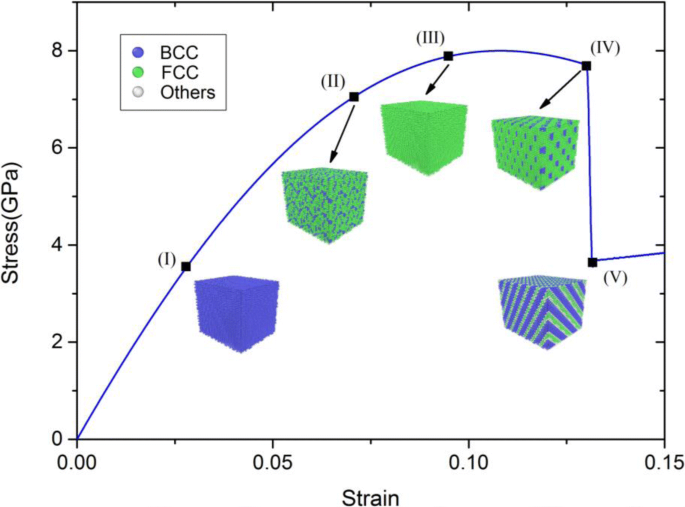
Curva tensión-deformación de Ta a presión cero y las correspondientes configuraciones con diferentes deformaciones. Notas:las bolas azules, verdes y blancas corresponden a BCC, FCC y otras estructuras de celosía, respectivamente
Como se muestra en la Fig. 3, se puede concluir a partir de la curva de tensión-deformación que la superficie se fractura cerca de la configuración (IV). Al comienzo de las deformaciones uniaxiales por tracción, la tensión cambia típicamente de forma lineal con la deformación y la figura 3I muestra que las configuraciones atómicas mantienen las estructuras BCC. A medida que aumenta la deformación, la transición de fase de las estructuras BCC a FCC comienza con la deformación de ~ 7,4% y se completa con la deformación de ~ 9,8%, como se muestra en las Fig. 3II, II, respectivamente. Y estas estructuras de FCC mantienen el máximo antes de la primera fractura de superficie. Cuando la deformación es ~ 13,1%, las longitudes de los bordes de las direcciones Y y Z disminuyen abruptamente, lo que resulta en una fractura de la superficie. Mientras tanto, es digno de mención que los conglomerados ocurren en muy poco tiempo, como se muestra en la Fig. 3IV. Bajo deformación uniaxial continua, la configuración atómica se mantiene en forma de franja hasta que la deformación es ~ 13,3%, que se muestra en la Fig. 3V.
En este artículo, nos concentramos en la dependencia de las propiedades de tracción en el tamaño del modelo, la velocidad de deformación, la temperatura y la presión, como se analiza en esta sección. Teóricamente, el modelo se estira linealmente en la etapa de deformación elástica y el módulo elástico se define como la pendiente de la porción lineal de la curva tensión-deformación. Se puede encontrar que todos los modelos tienen un proceso de estiramiento similar y las curvas de tensión-deformación tienen tendencias de variación similares. Por lo tanto, usamos el mismo enfoque para obtener el módulo elástico de Ta de varios tamaños de modelo y tasas de deformación.
Dependencia del tamaño y la tasa de deformación
La Tabla 2 enumera el módulo elástico y la tensión de fluencia de los diferentes tamaños de modelo a la temperatura de 1 K y la tasa de deformación de 5 × 10 8 s - 1 . Se puede concluir fácilmente que los tamaños de los modelos no tienen efectos sobre el módulo elástico y la tensión de fluencia de Ta. Es muy fácil de explicar que el módulo de elasticidad describe la interacción entre átomos, mientras que el módulo de elasticidad no varía con los tamaños del modelo. Puede verse en la Tabla 2 que el módulo elástico es ~ 139 GPa, notablemente igual que el resultado de la simulación de 140 GPa [18].
Según las Refs existentes. [28, 29], la mayoría de las tasas de deformación oscilan entre 10 8 s - 1 a 10 10 s - 1 . En este documento, se seleccionan cuatro tasas de deformación para realizar simulaciones de tracción, incluidas 5.0 × 10 8 s - 1 , 7,5 × 10 8 s - 1 , 5,0 × 10 9 s - 1 y 7,5 × 10 9 s - 1 . La Tabla 3 enumera el módulo de elasticidad y la tensión de fluencia a una temperatura de 300 K y a diferentes velocidades de deformación. Se puede concluir fácilmente que la tasa de deformación no tiene efectos obvios sobre el módulo elástico y la tensión de fluencia.
Mientras tanto, también simulamos los efectos del tamaño del modelo y la tasa de deformación sobre el módulo elástico y la tensión de fluencia a diferentes temperaturas y presiones. Estas simulaciones llegan a la misma conclusión. Por lo tanto, usaremos el mismo tamaño de modelo de 3,96 nm y la misma tasa de deformación de 5 × 10 8 s - 1 para las siguientes simulaciones.
Dependencia de la temperatura
La Figura 4 muestra las curvas de tensión-deformación a diferentes temperaturas hasta 1500 K. Se puede ver que las pendientes de estas curvas que denotan el módulo de elasticidad en la orientación <100>, es decir, E 100 , durante el período de tensión elástica y la tensión de fluencia están disminuyendo gradualmente con el aumento de temperatura. Según la teoría de la termodinámica [31], la energía cinética total de todos los átomos del sistema generalmente satisface la siguiente ecuación:
$$ {E} _ {\ mathrm {k}} =\ sum \ limits_ {i =1} ^ N \ frac {1} {2} {mv_i} ^ 2 =\ frac {3} {2} {Nk} _BT $$ (2)donde E k es la energía cinética total del sistema; N es el número total de átomos; K B es la constante de Boltzmann; T es la temperatura termodinámica. Por tanto, se puede concluir que el sistema contiene mayor energía cinética total a mayor temperatura y los átomos se mueven más rápido. Desde el punto de vista termodinámico, los átomos se vuelven más activos y el movimiento de los átomos es más intenso, lo que significa mayor amplitud en su posición de equilibrio. En el proceso de estiramiento, la fuerza de atracción entre los átomos se reduce relativamente y los átomos escapan fácilmente de la posición de equilibrio, por lo que la tensión en la dirección x se reduce con la misma deformación. Por tanto, el módulo elástico a mayor temperatura será menor que el de menor temperatura. Además, la tendencia de estas curvas concuerda bien con los primeros hallazgos teóricos y experimentales de Ta [6, 7, 32].
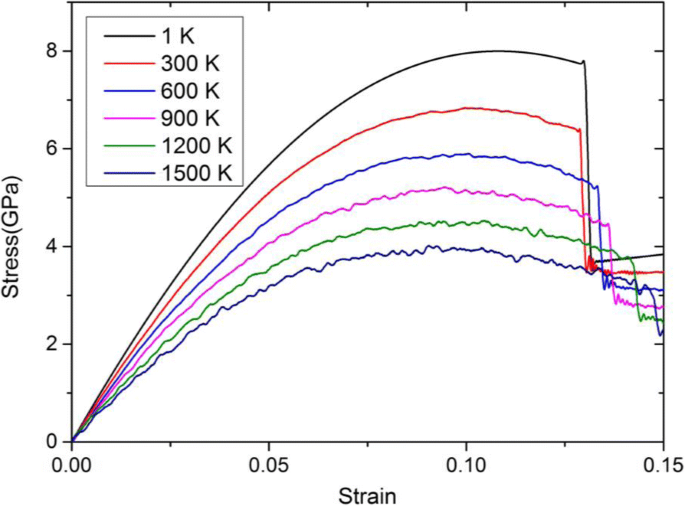
Curvas de tensión-deformación del modelo Ta de 3,96 nm a una tasa de deformación de 5 × 10 8 s - 1 y diferentes temperaturas de 1 a 1500 K. Se puede ver en la Fig.4 que las pendientes de estas curvas que denota el módulo elástico en la orientación <100>, es decir, E 100 , durante el período de tensión elástica y la tensión de fluencia están disminuyendo gradualmente con el aumento de temperatura
Para facilitar la observación, la Tabla 4 enumera el módulo elástico y la tensión de fluencia de Ta a diferentes temperaturas. El módulo elástico disminuirá ~ 42,3% de 136,49 a 76,67 GPa, y la tensión de fluencia disminuirá ~ 51% de ~ 8 a ~ 4 GPa a medida que la temperatura aumente de 1 a 1500 K.
De acuerdo con la Tabla 4, podemos derivar además una parametrización de la dependencia de la temperatura del módulo elástico ( E 100 ) Los resultados se muestran como una línea continua en la Fig. 5a. La parametrización dice lo siguiente:
$$ {E} _ {100} =a + {b} ^ {\ ast} T $$ (3)donde E 100 está en (GPa) y T se expresa en ( K ); a =138,07 ± 0,92111 y b =- 0,04094 ± 0,00101. Esta ecuación muestra que E 100 disminuye linealmente con el aumento de temperatura, y se recomienda su uso hasta la temperatura de 0 a 1500 K. De la ecuación. (3), se puede obtener fácilmente que E 100 alcanzará 0 GPa a la temperatura de T crítico =- a / b =3372 K, que está muy cerca de la temperatura de fusión de Ta [15].
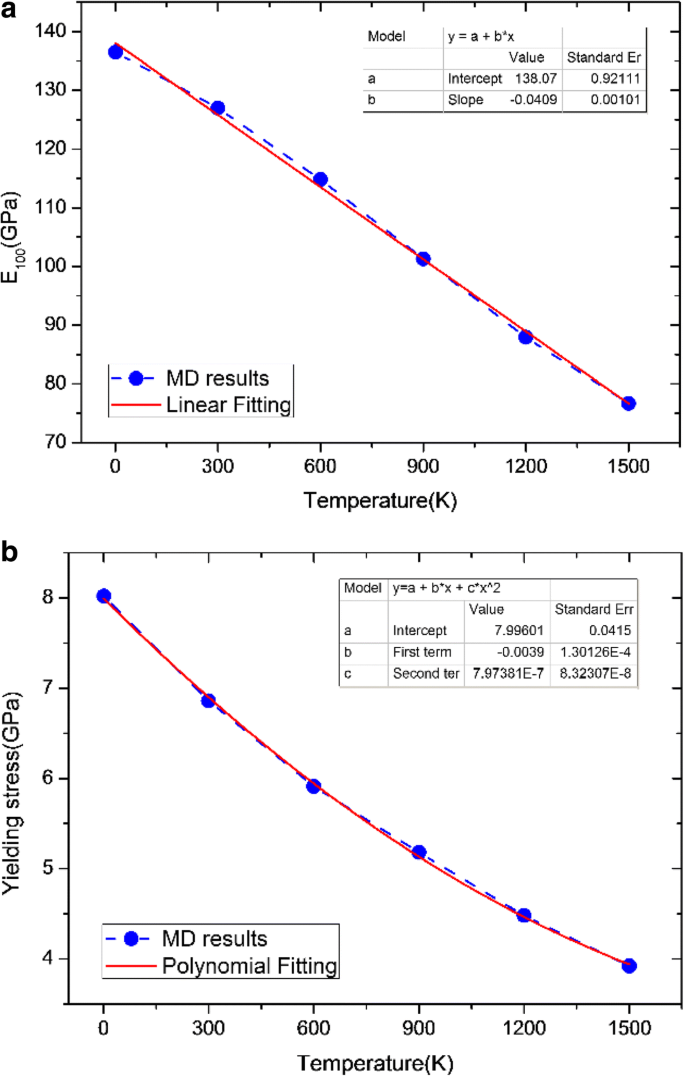
un Módulo de elasticidad y b tensión de fluencia frente a temperatura para Ta. En la Fig. 5, también presentamos una parametrización de la dependencia de la temperatura del módulo elástico ( E 100 ) resultados
Para el límite elástico, la parametrización recomendada es
$$ {Y} _ {\ mathrm {estrés}} =a + {b} ^ {\ ast} T + {c} ^ {\ ast} {T} ^ 2 $$ (4)donde Y estrés está en (GPa) y T se expresa en ( K ); a =7,99610 ± 0,0415, b =- 0,0039 ± 1,30126 × 10 - 4 y c =7,97381 × 10 - 7 ± 8,32307 × 10 - 8 . De la ecuación. (4), se puede encontrar que la tensión de fluencia probablemente disminuya con la temperatura conformando un modelo polinomial cuadrático, como se muestra en la línea continua en la Fig. 5b.
Dependencia de la presión
Como se mencionó en la sección “Introducción”, se han realizado extensos esfuerzos teóricos y experimentales sobre las propiedades termoelásticas del Ta en condiciones de alta presión. A diferencia de los métodos estáticos, adoptamos un método dinámico a través de <100> carga de tracción para examinar su dependencia de la presión del módulo elástico de E 100 bajo diferente presión hidrostática.
La figura 6 muestra las curvas del módulo elástico de E 100 versus la presión hasta 140 GPa a diferentes temperaturas de 1 a 1500 K. Si bien todas las líneas continuas con diferentes colores se obtienen mediante un método dinámico a diferentes temperaturas, la línea de puntos con marcadores cuadrados se obtiene mediante un método estático utilizando la Ec. (1) basado en los valores de C 11 y C 12 a 0 K. Es obvio que la curva a 1 K, es decir, la línea sólida roja con marcadores circulares, casi se superpone con la curva obtenida mediante un método estático (la línea de puntos), lo que denota que el método dinámico adoptado en la presente el trabajo es aplicable a alta presión de hasta 140 GPa.
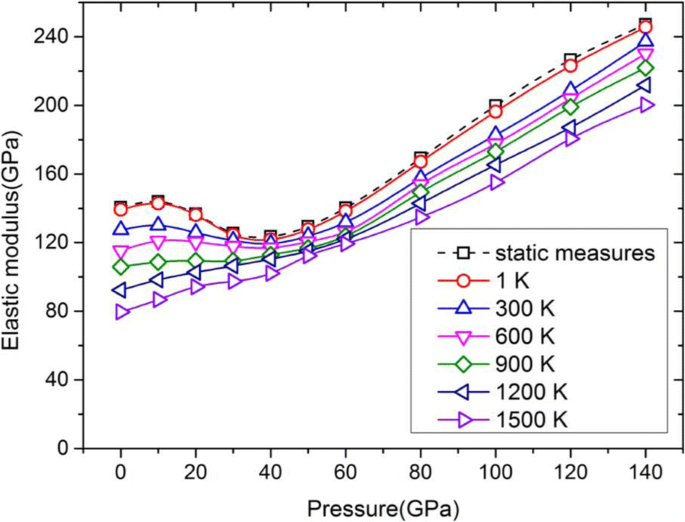
Módulo elástico en orientación <100> de Ta a diferentes temperaturas y presiones. Cabe señalar que el módulo de elasticidad de estas curvas es E 100
Como se ilustra en la Fig.6, el módulo elástico de E 100 a una temperatura no superior a 600 K muestra una sección cóncava hacia abajo a medida que la presión aumenta de 20 a 60 GPa. Ruestes et al. [18] informó las constantes elásticas en función de la presión hasta 60 GPa mediante el uso de simulaciones MD, y los resultados concuerdan bien con el C calculado 11 y C 12 en el trabajo actual. A cambio, el módulo elástico calculado de E 100 también muestra la misma tendencia con nuestros resultados. Pero el módulo elástico calculado de E 100 de los cálculos de DFT [33] aumenta gradualmente con la presión creciente, y no se encuentra una sección cóncava hacia abajo en las curvas. ¿Qué hace que ocurra esta inconsistencia? En general, los potenciales utilizados en las simulaciones MD se obtienen ajustando los cálculos DFT y los resultados experimentales. En este sentido, los cálculos de DFT tienen mayor precisión que el método MD. El potencial Ravelo-EAM [21] se construye introduciendo propiedades de alta presión en la curva de ajuste de la ecuación de estado (EOS) DFT de los monocristales de Ta. Durante el procedimiento de ajuste, la curva fría de EOS se extiende para incluir términos de orden superior (cúbicos y cuárticos) de constante de celosía, lo que hace que MD EOS sea muy sensible a los términos de orden superior de constante de celosía. En otras palabras, esta inconsistencia puede deberse a que el potencial Ravelo-EAM no podría describir con precisión el EOS de Ta bajo la presión de 20 a 60 GPa. En general, se puede concluir que las curvas del módulo elástico frente a la presión tienen una tendencia similar a diferentes temperaturas, y el módulo elástico aumenta gradualmente con el aumento de la presión por encima de ~ 40 GPa.
Conclusiones
En este artículo, se ha realizado una simulación de MD para investigar las dependencias de temperatura y presión de las propiedades elásticas de los monocristales de Ta a través de una carga de tracción <100>. Al principio, hicimos un estudio comparativo sobre dos tipos de potenciales EAM, incluidos Zhou-EAM y Ravelo-EAM, en términos de las propiedades elásticas de Ta a 0 K y diferentes presiones hidrostáticas. Los resultados muestran que el potencial Ravelo-EAM se comporta mejor que el potencial Zhou-EAM bajo diferentes presiones. Luego, se llevan a cabo simulaciones MD sobre los comportamientos de tracción de los monocristales de Ta basados en el potencial Ravelo-EAM. Las observaciones muestran que Ta experimentará una transición de fase BCC-FCC antes de la fractura bajo una carga de tracción <100>, y el tamaño del modelo y la velocidad de deformación no tienen una influencia obvia en los comportamientos de tracción de los monocristales de Ta. Además, el módulo elástico de E 100 disminuirá linealmente de ~ 136 a ~ 79 GPa con el aumento de temperatura de 1 a 1500 K, y la tensión de fluencia disminuirá de ~ 8 a ~ 4 GPa con el aumento de temperatura, conformando una fórmula polinomial cuadrática. Finalmente, la dependencia de la presión de las propiedades elásticas se realiza de 0 a 140 GPa, y las observaciones muestran que el módulo elástico aumenta con el aumento de la presión en general. Los resultados de las simulaciones MD también muestran que el potencial Ravelo-EAM se comporta bien a una presión más alta y la fórmula para el cálculo de E 100 usando C 11 y C 12 a una presión inferior a 140 GPa.
Historial de cambios
Abreviaturas
- CCO:
-
Cúbico centrado en el cuerpo
- DAC:
-
Celda de yunque de diamante
- DFT:
-
Teoría funcional de la densidad
- EAM:
-
Método de átomo incrustado
- EFS:
-
Finnis-Sinclair extendido
- EOS:
-
Ecuación de estado
- FCC:
-
Cúbico centrado en la cara
- LAMMPS:
-
Simulador paralelo masivo atómico / molecular a gran escala
- MD:
-
Dinámica molecular
- NPT:
-
Conjunto isotérmico-isobárico
- NVT:
-
Conjunto canónico
- OVITO:
-
Herramienta de visualización abierta
- PBC:
-
Condiciones de contorno periódicas
- Ta:
-
Tantalio
Nanomateriales
- Propiedades y aplicaciones del tantalio
- Efecto superficial sobre el transporte de petróleo en nanocanales:un estudio de dinámica molecular
- Modelado y simulación de dinámica molecular del corte con diamante de cerio
- Estudio de los primeros principios sobre la estabilidad y la imagen STM del borofeno
- El efecto del plasma de no equilibrio por contacto sobre las propiedades estructurales y magnéticas de Mn Х Fe3 - X О4 Espinelas
- Influencia del agua en la estructura y propiedades dieléctricas de la microcristalina y nanocelulosa
- Efectos del espesor de la bicapa en las propiedades morfológicas, ópticas y eléctricas de los nanolaminados de Al2O3 / ZnO
- Ajuste de las morfologías de la superficie y las propiedades de las películas de ZnO mediante el diseño de la capa interfacial
- Estudio del efecto de la dirección de impacto en el proceso de corte nanométrico abrasivo con dinámica molecular
- Preparación y propiedades ópticas de las películas GeBi mediante el método de epitaxia de haz molecular
- La diferencia entre presión y caudal



