Modelado y simulación de dinámica molecular del corte con diamante de cerio

Métodos

Modelo MD de corte de diamante

La Figura 1 muestra el modelo MD de corte de diamante, que consta de una pieza de trabajo de cerio monocristalino y una herramienta de corte de diamante. La pieza de cerio tiene una dimensión de 41, 25 y 31 nm en dirección horizontal, vertical y longitudinal, respectivamente, y consta de un millón de átomos de γ-Ce en estructura fcc. La condición de contorno periódica solo se aplica en dirección longitudinal. La pieza de trabajo consta de dos tipos de átomos, como átomos inferiores y átomos móviles, respectivamente. La capa de átomos inferiores con un espesor de 2 nm se fija en el espacio para evitar cualquier movimiento rígido de la pieza de trabajo. El movimiento de los átomos móviles sigue la ecuación de movimiento de Newton con el algoritmo de integración velocidad-verlet. La temperatura de cada átomo en la pieza de trabajo se monitorea en el proceso de corte para representar la disipación de calor generada. Para abordar la influencia de la orientación cristalográfica, se consideran tres piezas de cerio con (010), (110) y (111) superficies libres en dirección vertical. La herramienta de corte de diamante con un borde afilado tiene un ángulo de relieve de 9 ° y está compuesta por 0,1 millones de átomos de C en estructura de diamante. Se utilizan siete ángulos de inclinación, como −30 °, −20 °, −10 °, 0 °, 10 °, 20 ° y 30 °, para abordar la influencia del ángulo de inclinación. Dada la dureza ultra alta del diamante en comparación con el cerio y la distancia de corte ultracorta, no se considera el desgaste de la herramienta de diamante durante el proceso de corte. Por lo tanto, la herramienta de corte de diamante se configura como un cuerpo rígido, es decir, las coordenadas y velocidades de todos los átomos de la herramienta de corte se actualizan en cada paso, de tal manera que la herramienta de corte se mueve como una sola entidad sin ninguna deformación.

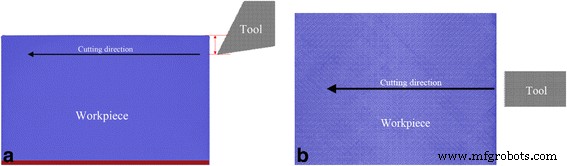
Modelo MD de corte de diamante de cerio; (color en línea) Modelo MD de corte de diamante de cerio. un Vista frontal y b vista superior . Rojo y colores azules representan átomos de Ce inferiores y móviles, y color gris indica átomos de C

Hay tres tipos de interacciones atómicas en el sistema simulado, como Ce-Ce en la pieza de trabajo de cerio, Ce-C entre la pieza de trabajo de cerio y la herramienta de corte de diamante, y C-C en la herramienta de corte de diamante, respectivamente. Las interacciones C-C se omiten ya que la herramienta de corte de diamante se trata como un cuerpo rígido sin ninguna deformación en el proceso de corte. El método del átomo incrustado (EAM) compuesto por un potencial de par que interactúa y la energía de incrustación de electrones se ha utilizado ampliamente para describir sistemas metálicos, que se pueden expresar como

donde r _ij es la distancia entre los átomos i y j , ϕ _ij es el potencial de par entre átomos i y j , F _i representa la energía de incrustación que se genera cuando un átomo i está incrustado, ρ _i es la densidad de electrones en i átomo generado por todos los átomos excepto el átomo i y ρ _j es una función de la densidad electrónica del átomo j en el átomo i . Los parámetros de EAM para el cerio de Sheng et al. se utilizan para describir las interacciones Ce-Ce, que es capaz de describir con precisión las propiedades elásticas en masa de las fases de cerio fcc [29]. El potencial Morse se utiliza para describir la interacción Ce-C, que se puede expresar como

donde D ₀ (0.087 eV) es la energía cohesiva, α (5.14) es el módulo elástico y r ₀ (2,93 Å) representa la distancia de equilibrio entre los átomos i y j , respectivamente. El radio de corte del potencial Morse se elige como 1.0 nm [30].

El sistema de simulación tal como se creó se equilibra primero a su configuración de equilibrio a 30 K y por debajo de 0 bar en el conjunto NPT (número constante de átomos N , presión constante P y temperatura constante T ). Luego, la pieza equilibrada se somete al corte de diamante con una velocidad constante de 100 m / sy una profundidad de corte de 4 nm en el conjunto canónico (número constante de átomos N , volumen constante V y temperatura constante T ). La dirección de corte se indica mediante flechas de color rojo en diferentes puntos de vista del modelo de corte. Y la fuerza de corte se define como el componente de fuerza a lo largo de la dirección de corte. La profundidad de corte utilizada en el experimento de mecanizado de ultra precisión es de unos pocos micrómetros. Observamos que la dimensión simulada de la pieza de trabajo y la profundidad de corte son varios órdenes de magnitud más pequeños que los utilizados en experimentos de corte de diamante de ultra precisión, debido a la limitación de la escala de longitud en las simulaciones atomísticas. También observamos que la velocidad de corte empleada de 100 m / s en las simulaciones MD actuales de corte nanométrico es varios órdenes de magnitud más alta que las velocidades típicas de decenas de micrómetros por segundo utilizadas en experimentos de corte de diamante de ultra precisión, lo que da el requisito intrínseco de la El paso de tiempo de integración debe ser del orden de femtosegundos (fs). El análisis de vecino común (CNA) se utiliza para identificar tipos de defectos de celosía [31], y el esquema de coloración es el siguiente:verde representa átomos fcc, rojo para átomos hexagonales compactos (hcp), azul para cúbicos centrados en el cuerpo (bcc) átomos y gris para otros átomos, incluidos los átomos de la superficie y los núcleos de dislocación. Todas las simulaciones de MD se realizan utilizando el código LAMMPS con un intervalo de tiempo de integración de 1 fs [32]. Y el OVITO se utiliza para visualizar datos MD y generar instantáneas MD [33].

Caracterización de las fases de cerio

En el presente trabajo se consideran cinco fases de cerio, como γ, α, β, ε y δ, respectivamente. La Tabla 1 enumera los parámetros estructurales y las condiciones de temperatura-presión relacionadas para cada fase que se recopilan de la literatura [8, 9, 10, 11]. La configuración atómica en masa de cada fase se construye luego de acuerdo con la Tabla 1. Y luego, se realizan simulaciones computacionales de tensión uniaxial, cizallamiento y compresión uniforme de configuraciones en masa tal como se construyeron para derivar las propiedades mecánicas de las diferentes fases de Ce. Debido a la alta temperatura estable cerca del punto de fusión del cerio, las propiedades mecánicas del δ-Ce no se calculan ya que es difícil realizar pruebas mecánicas en la fase líquida. La Tabla 2 enumera las constantes elásticas derivadas y las propiedades mecánicas de cada fase de cerio. El módulo de Young calculado de la fase γ-Ce monocristalina es 24,17 GPa, que es comparable con el valor experimental de 36,7 GPa informado en la nanoindentación de su contraparte policristalina [10]. Además, los valores calculados de C44 y 1/2 (c11-c12) difieren en un factor de 3, lo que concuerda bien con el valor experimental mediante el uso de técnicas de dispersión de neutrones inelásticos [34]. La Tabla 2 demuestra que el α-Ce más denso tiene propiedades mecánicas significativamente mejoradas en comparación con su fase γ-Ce isoestructural de baja densidad.

La función de distribución radial (RDF), definida como las variaciones de densidad en un sistema de partículas con la distancia desde una partícula de referencia en forma de picos agudos. El RDF puede deducirse de los espectros de rayos X y los datos de difracción de neutrones [35, 36]. Por lo tanto, es una de las herramientas más importantes para la caracterización estructural de líquidos y sólidos por igual y actúa como un vínculo importante entre los arreglos atómicos microscópicos y las propiedades macroscópicas. En el estudio actual, el RDF se utiliza para caracterizar las diferencias estructurales entre las diferentes fases del cerio. La Figura 2a traza los histogramas RDF para las cinco fases de cerio, en las que los picos representan características de la estructura de celosía correspondiente:la primera, segunda y tercera distancia de vecino más cercano de γ-Ce es 3.64, 5.13 y 6.3 Å, respectivamente; la primera, segunda y tercera distancia de vecino más cercano de α-Ce es 3,41, 4,85 y 5,92 Å, respectivamente; la distancia del primer y segundo vecino más cercano de δ-Ce es 3,53 y 6,75 Å, respectivamente; la primera, segunda, tercera y cuarta distancia de vecino más cercano de ε-Ce es 2,96, 3,33, 4,91 y 5,69 Å, respectivamente; la primera, segunda, tercera y cuarta distancia de vecino más cercano de β-Ce es 3.71, 3.97, 5.27 y 5.92 Å, respectivamente. Para demostrar la viabilidad de predecir transformaciones de fase entre dos fases de cerio fcc mediante los parámetros de potencial EAM empleados, se realiza la compresión uniforme del volumen γ-Ce hasta lograr un colapso de volumen del 20%. La Figura 2b presenta el RDF antes y después de la compresión, que coincide respectivamente bien con el RDF de γ-Ce y α-Ce, lo que indica la ocurrencia de la transformación de fase γ ➔ α más conocida [12,13,14] .

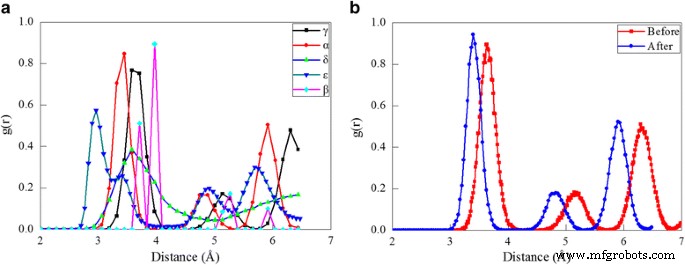
Análisis RDF de fases de cerio; (color en línea) a RDF de fases de cerio. b RDF antes y después de la compresión de γ-Ce

Resultados y discusión

Mecanismos de mecanizado de cerio

La simulación MD del corte con diamante de Ce (010) se realiza en primer lugar para dilucidar los mecanismos fundamentales de mecanizado del cerio. La herramienta de corte de diamante utilizada tiene un ángulo de ataque de 0 °. Hay tres componentes de la fuerza de mecanizado, como fuerza de corte a lo largo de la dirección horizontal, fuerza normal perpendicular a la superficie mecanizada y fuerza lateral a lo largo de la dirección longitudinal, respectivamente. La Figura 3 muestra las variaciones de la fuerza de corte y la fuerza normal con la longitud de corte durante el proceso de corte, que se clasifican en tres zonas según la longitud de corte. En consecuencia, la subfigura en cada zona muestra una configuración de corte representativa, en la que los átomos están coloreados de acuerdo con sus valores de CNA, y los átomos fcc no se muestran para una visualización clara de los defectos.

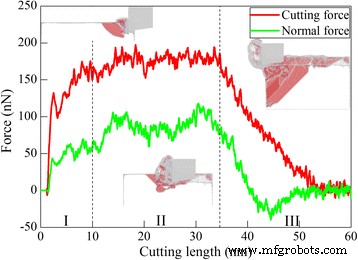
Variación de la fuerza de mecanizado; (color en línea) variación de la fuerza de corte y la fuerza normal con la longitud de corte durante el corte con diamante de Ce (010) bajo un ángulo de ataque de 0 °. Las subfiguras presentan configuraciones de defectos representativas en diferentes zonas, en las que los átomos están coloreados de acuerdo con sus valores de CNA

Se ve en la Fig. 3 que tanto la fuerza de corte como la fuerza normal tienen valores negativos cuando la herramienta de corte está muy cerca de la pieza de trabajo, debido a la adhesión entre la herramienta de corte y la pieza de trabajo. Cuando la herramienta de corte comienza a entrar en contacto con la pieza de trabajo, el material sufre en primer lugar una deformación elástica, acompañada de rápidos aumentos tanto de la fuerza de corte como de la fuerza normal. La Figura 3 muestra que tanto la fuerza de corte como la fuerza normal caen rápidamente a una longitud de corte de 2,3 nm, lo que indica el inicio de la deformación plástica. Al cortar más, tanto la fuerza de corte como la fuerza normal aumentan con fuertes fluctuaciones causadas por sucesivos eventos de nucleación. En la subfigura de la zona II se ve que hay una considerable dislocación parcial 1/6 <112> Shockley generada en las proximidades de la zona de corte. Tanto la fuerza de corte como la fuerza normal fluctúan principalmente alrededor de valores constantes en la longitud de corte que van de 10 a 35 nm, lo que indica que el proceso de corte es estable. Y las dislocaciones en la zona II residen principalmente tanto delante como debajo de la herramienta de corte de diamante. Cuando la longitud de corte alcanza los 35 nm, la herramienta de corte comienza a separarse de la pieza de trabajo, acompañada de disminuciones significativas tanto de la fuerza de corte como de la fuerza normal. La subfigura en la zona III muestra que hay considerables dislocaciones bloqueadas por el lado izquierdo de la pieza de trabajo. Tanto la fuerza de corte como la fuerza normal se estabilizan hasta que la viruta formada se separa completamente de la pieza de trabajo. La Figura 3 muestra que durante el proceso de corte, la fuerza normal es menor que la fuerza de corte.

La Figura 4a – d presenta estructuras defectuosas instantáneas dentro de la pieza de trabajo en diferentes longitudes de corte. Los átomos se colorean de acuerdo con sus valores de CNA y no se muestran los átomos de fcc. En consecuencia, la Fig. 4e-h presenta morfologías de superficies mecanizadas coloreadas por sus alturas atómicas. La inspección dinámica de la evolución del defecto muestra que la deformación de la pieza de trabajo está acompañada por la nucleación de 1/6 <112> dislocaciones parciales de Shockley desde la superficie libre del lado derecho y su deslizamiento posterior en planos de deslizamiento {111} adyacentes ya lo largo de direcciones de deslizamiento <110>. El movimiento de las dislocaciones parciales de Shockley se acompaña de la expansión de las fallas de apilamiento que están limitadas por núcleos de dislocación. Con el progreso del proceso de corte, se emite una gran cantidad de dislocaciones parciales desde la superficie libre superior frente a la herramienta de corte, lo que conduce a la formación de virutas considerables a lo largo de la cara de desprendimiento de la herramienta de corte, como se muestra en la Fig. 4f. Simultáneamente, las dislocaciones detrás de la herramienta de corte se mueven hacia arriba para aniquilarse en la superficie libre superior, lo que lleva a una recuperación significativa de la superficie mecanizada. La figura 4c muestra que cuando la herramienta de corte se acerca al límite izquierdo de la pieza de trabajo, la propagación de las dislocaciones está fuertemente bloqueada por la superficie libre del lado izquierdo, acompañada de un volumen de viruta significativamente mayor, como se muestra en la figura 4g. La Figura 4d muestra que después de la separación completa entre la viruta y la pieza de trabajo, la densidad de dislocación dentro de la pieza de trabajo disminuye significativamente debido a la aniquilación de la dislocación en la superficie libre superior.

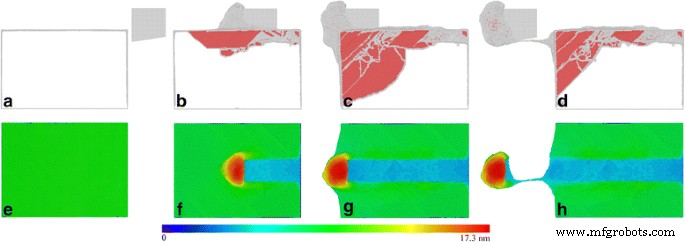
Estructuras defectuosas y morfologías de superficies mecanizadas; (color en línea) Instantáneas MD de estructuras de defectos instantáneas ( fila superior ) y morfología de la superficie mecanizada ( fila inferior ) en el corte de diamante de Ce (010) con un ángulo de ataque de 0 °. Longitudes de corte: a , e 0,0 nm, b , f 18,8 nm, c , g 44,8 nm y d , h 59,6 nm. Átomos en la fila superior y fila inferior están coloreados de acuerdo con sus valores de CNA y alturas atómicas, respectivamente

Además de la plasticidad dominada por el deslizamiento de la dislocación, la probabilidad de transformación de fase en el proceso de corte de diamante también se evalúa realizando un análisis RDF en la zona del defecto dentro de la pieza de trabajo y las virutas formadas. La γ-Ce en la estructura fcc se excluye primero en OVITO mediante el uso del algoritmo CNA, y el resto de átomos se componen de zonas defectuosas que incluyen bcc, hcp y otros átomos. Luego, se realiza un análisis RDF en la zona del defecto. Y la cantidad de diferentes fases de Ce se puede deducir por el número de diferentes tipos de átomos defectuosos. La Figura 5a muestra que los tres picos del RDF de la zona de defecto debajo de la superficie mecanizada coinciden bien con los tres picos exactos del RDF del δ-Ce, lo que sugiere la ocurrencia de transformación de fase del γ-Ce al δ-Ce. Si bien el δ-Ce es estable a alta temperatura y baja presión, la transformación de fase γ ➔ δ ocurrida indica la alta disipación de calor generada en el proceso de corte. Además, dado que el δ-Ce tiene diferentes propiedades mecánicas de la fase γ-Ce, el δ-Ce generado conduce a un mecanizado heterogéneo en el proceso de corte posterior. La Figura 5b indica que también se detectan átomos de δ-Ce en las virutas formadas, principalmente debido a la transformación de fase γ ➔ δ activada por alta temperatura en la región de contacto entre la viruta formada y la superficie inclinada de la herramienta de corte. Sin embargo, la cantidad de δ-Ce formado tanto en la zona del defecto como en la viruta es muy trivial, lo que indica que la transformación de fase no es prominente en el corte de diamante de cerio.

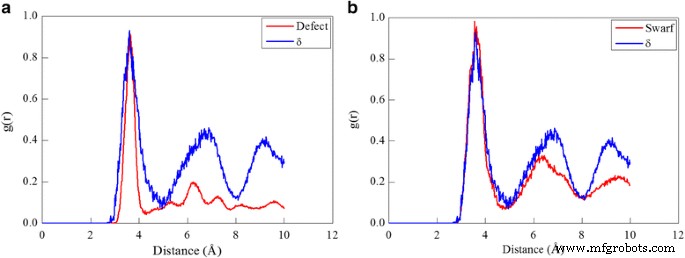
Análisis de transformación de fase en proceso de corte; (color online) análisis de la transformación de fase en el corte de diamante de Ce (010) bajo un ángulo de ataque de 0 °. RDF de a pieza de trabajo y b viruta después del corte

Influencia del ángulo de ataque

Con el conocimiento fundamental de los mecanismos de mecanizado del cerio, se estudia la influencia del ángulo de ataque de la herramienta de corte en el corte de diamante. La Figura 6 traza los valores promediados tanto de la fuerza de corte como de la fuerza normal para los siete ángulos de inclinación. El valor promedio de cada componente de fuerza se calcula promediando los valores de fuerza instantáneos en la longitud de corte que van de 10 a 35 nm. La Figura 6 muestra que la fuerza de corte es mayor que la fuerza normal para cada ángulo de inclinación. Sin embargo, el valor diferencial de los dos componentes de fuerza es más pronunciado para un ángulo de ataque mayor. Además, tanto la fuerza de corte como la fuerza normal disminuyen al aumentar el ángulo de ataque. De acuerdo con la teoría de Merchant, con el aumento del ángulo de ataque, el ángulo del plano de corte correspondiente a la energía mínima también aumenta, lo que en consecuencia disminuye la fuerza de corte [37]. La variación de la fuerza de mecanizado dependiente del ángulo de desprendimiento revelada por las simulaciones MD actuales concuerda bien con la teoría de Merchant.

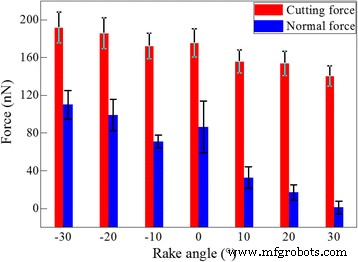
Dependencia del ángulo de desprendimiento de la fuerza de mecanizado; (color en línea) influencia del ángulo de ataque en la fuerza de mecanizado

La Figura 7a, b presenta una vista inferior de la estructura defectuosa debajo de la superficie mecanizada después de completar el proceso de corte con diamante con un ángulo de inclinación de -30 ° y 30 °, respectivamente. Para cada ángulo de inclinación, los tipos de dislocación y la geometría de la dislocación con respecto a la superficie libre son iguales. Sin embargo, la densidad de dislocación es significativamente mayor para el ángulo de inclinación de -30 ° que el ángulo de inclinación de 30 °, lo que indica que se produjo una deformación plástica más compleja. La Figura 7c presenta el número de segmentos de dislocación que permanecieron dentro de la pieza de trabajo después del corte con diamante con diferentes ángulos de inclinación, lo que indica que la densidad de dislocación disminuye al aumentar el ángulo de inclinación. Cabe señalar que diferentes tipos de dislocaciones categorizadas por los vectores de Burgers, incluyendo 1/2 <110> dislocación perfecta, 1/6 <112> dislocación parcial de Shockley, 1/6 <110> dislocación de varilla de escalera y 1/3 <111> Las dislocaciones parciales francas se tienen en cuenta en la Fig. 7c. En el proceso de corte nanométrico, la deformación microscópica mediada por dislocación del material de la pieza de trabajo tiene una fuerte correlación con los resultados del mecanizado macroscópico en términos de fuerza de mecanizado y morfología de la superficie mecanizada. Por ejemplo, la interacción y reacción de las dislocaciones conduce a la formación de estructuras de dislocación sésiles que bloquean el movimiento de la dislocación posterior; en consecuencia, el endurecimiento por trabajo resultante conduce a un aumento de la fuerza de mecanizado. La aniquilación de las dislocaciones en la superficie libre conduce a la recuperación de la superficie mecanizada, acompañada de la formación de un apilamiento superficial [38].

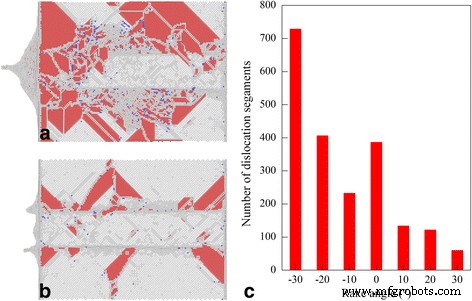
Estructuras defectuosas generadas con diferentes ángulos de ataque; (color en línea) Instantáneas de MD de estructuras defectuosas después de cortar Cerio con un ángulo de inclinación de a −30 ° y b 30 °. Los átomos se colorean de acuerdo con sus valores de CNA. c Número de dislocación dependiente del ángulo de inclinación

La Figura 8 presenta las morfologías de la superficie mecanizada después de la finalización de los procesos de corte para diferentes ángulos de ataque. El volumen de la superficie apilada en ambos lados de la ranura formada es más pronunciado para el ángulo de inclinación con valores negativos que con valores positivos. Además, la distribución del amontonamiento de la superficie es menos uniforme para el ángulo de ataque negativo que para el ángulo de ataque positivo. La Figura 8c muestra claramente la distribución de asimetría de la superficie apilada a lo largo de la ranura formada para el ángulo de inclinación de -30 °. Se ve en la Fig. 8 que el volumen de la superficie apilada disminuye al aumentar el ángulo de inclinación. Por lo tanto, se indica que el ángulo de ataque de 30 ° es óptimo para el corte de diamante de cerio para la fuerza de mecanizado más baja, la densidad de dislocación más baja y el apilamiento de superficie más bajo que los otros ángulos de ataque.

Dependencia del ángulo de desprendimiento de las morfologías de la superficie mecanizada; (color en línea) morfología de la superficie mecanizada con diferentes ángulos de ataque: a −10 °, b −20 °, c −30 °, d 10 °, e 20 ° y f 30 °. Los átomos se colorean de acuerdo con sus alturas atómicas

Influencia de la orientación del cristal de la pieza de trabajo de cerio

También se investiga la influencia de la orientación del cristal en el corte de diamante de cerio bajo el ángulo de inclinación óptimo de 30 °. Todos los parámetros de mecanizado son iguales para Ce (010), Ce (110) y Ce (111). La Figura 9 muestra variaciones de la fuerza de corte y el número de dislocaciones con diferentes orientaciones de cristal. La fuerza de corte de Ce (010) es significativamente menor que la de Ce (110) y Ce (111). Aunque el número de dislocaciones es el más bajo en Ce (111), la densidad de dislocaciones en Ce (010) es significativamente menor que en Ce (110). Se sabe que la geometría entre el plano de deslizamiento y la superficie libre varía con la orientación del cristal. Tanto para Ce (010) como para Ce (110), los cuatro planos de deslizamiento {111} están inclinados hacia la superficie mecanizada. Sin embargo, hay un plano de deslizamiento {111} paralelo a la superficie mecanizada de Ce (111), además de tres planos de deslizamiento inclinados {111}. While microscopic deformation of workpiece material is dominated by dislocation slips, the observed macroscopic machining results in terms of machined surface and machining force can also be influenced by machined surface morphology. Although the easy glide of dislocations on the {111} slip plane parallel to free surface is energetically favorable for the accommodation of plastic strain caused by cutting tool action, the resulting considerable surface pile up increases the machining resistance, which leads to a high cutting force.

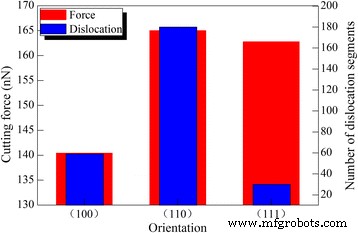
Crystal orientation dependence of cutting force and dislocation number; (color online) crystal orientation dependence of cutting force and dislocation number

Figure 10a–c presents machined surface morphology of Ce(010), Ce(110), and Ce(111), respectively, indicating that the crystal orientation has a strong influence on machined surface quality. The volume of surface pile up is the smallest for Ce(010), followed by Ce(111), and the largest for Ce(110). Correspondingly, the material removal in the form of chip is the most pronounced for Ce(010). Furthermore, it is seen that the surface pile up of Ce(111) on both side of formed groove presents the highest symmetry, while that of Ce(110) is the worst. Therefore, it is indicated that the crystal orientation of (010) is optimal for the diamond cutting of cerium due to its low machining force, low dislocation density, and low surface pile up.

Crystal orientation dependence of machined surface morphology; (color online) crystal orientation dependence of machined surface morphology. Atoms are colored according to atomic heights. Crystal orientation. un (010). b (110). c (111)

Conclusiones

In summary, we perform MD modeling and simulation to elucidate the underlying mechanisms of cerium under the ultra-precision diamond cutting. The EAM and Morse potentials are respectively employed to describe atomic interactions within cerium workpiece and the interactions between cerium workpiece and diamond cutting tool. The elastic constants, mechanical properties, and propensity of phase transformation of cerium phases are evaluated, which demonstrates the feasibility of predicting phase transformation of cerium by the current established MD model. Subsequent MD simulations of diamond cutting reveal that the plastic deformation of cerium is governed by dislocation nucleation and subsequent glide, which is similar with other fcc metals. In addition, there is γ ➔ δ phase transformation occurred within both machined surface and formed chip. It is found that high quality of machined surface and low machining force can be achieved in the diamond cutting of cerium with the optimal machining conditions, i.e., a rake angle of 30° for a crystal orientation of (010).

Absorbedor perfecto de banda ancha con monocapa MoS2 y matriz de nanodiscos de nitruro de titanio hexagonal Estrategia de sinterización asistida por hidrotermia hacia material de ánodo LiNb3O8 de estructura hueca y porosa