Estudio del efecto de la dirección de impacto en el proceso de corte nanométrico abrasivo con dinámica molecular

Resumen

El pulido de flujo abrasivo juega un papel importante en el mecanizado moderno de ultra precisión. Las partículas ultrafinas suspendidas en el medio del flujo abrasivo eliminan el material en nanoescala. En este artículo, se realizan simulaciones tridimensionales de dinámica molecular (MD) para investigar el efecto de la dirección de impacto en el proceso de corte abrasivo durante el pulido con flujo abrasivo. Se utilizó el software de simulación de dinámica molecular Lammps para simular el corte de cobre monocristalino con granos abrasivos de SiC en diferentes ángulos de corte (0 ^o –45 ^o ). A un coeficiente de fricción constante, encontramos una relación directa entre el ángulo de corte y la fuerza de corte, lo que finalmente aumenta el número de dislocaciones durante el mecanizado de flujo abrasivo. Nuestro estudio teórico revela que un ángulo de corte pequeño es beneficioso para mejorar la calidad de la superficie y reducir los defectos internos en la pieza de trabajo. Sin embargo, no existe una relación obvia entre el ángulo de corte y el coeficiente de fricción.

Antecedentes

En el mecanizado moderno de ultraprecisión, las tecnologías de eliminación de material juegan un papel importante en la fabricación de elementos microelectrónicos, micromecánicos y ópticos. La demanda de dispositivos miniaturizados con alta precisión dimensional y calidad superficial, hacen que los procesos de ultraprecisión sean la principal opción en el campo mencionado [1]. Además, los cambios de los componentes de la superficie y la estructura de la subsuperficie se encuentran en la escala de longitud nanométrica. La tecnología de pulido por flujo de partículas abrasivas juega un papel importante en muchos campos del mecanizado de precisión y es como otras tecnologías de acabado no tradicionales que mejoran la calidad de la superficie. Esta tecnología ha atraído a muchos investigadores debido a su importante papel. E. Uhlmann y otros investigadores han informado de la simulación por computadora de una superficie de cerámica de pulido de grano abrasivo para los experimentos diseñados para verificar el flujo de fluido de molienda de varios factores de procesamiento sobre el efecto de los materiales de corte [2]. Sehijpal Singh y otros investigadores utilizan la tecnología de pulido de flujo abrasivo para cortar materiales de cobre y aluminio. A partir del análisis de microscopía electrónica de barrido, encontraron una superficie de ranura profunda en su pieza de trabajo [3]. G. Venkatesh y otros investigadores han informado sobre la tecnología de pulido de grano abrasivo asistido por ultrasonidos para el engranaje cónico en la compleja superficie del proceso de acabado. En esta técnica, la velocidad del grano abrasivo es más alta que el flujo de grano abrasivo convencional para chocar con la superficie de la pieza de trabajo, lo que puede mejorar la eficiencia del procesamiento. A partir de sus métodos experimentales y teóricos, encontraron que esta tecnología es una de las mejores opciones para el acabado de palas de engranajes [4, 5]. K. Kamal y col. estudiaron las propiedades reológicas del líquido abrasivo en la viscosidad abrasiva del fluido, la velocidad de cizallamiento y el tiempo de fluencia [6]. Sin embargo, la mayoría de los estudios de pulido por flujo abrasivo se basan en el nivel macro y se ha prestado muy poca atención al nivel micro. En el proceso de pulido de flujo abrasivo, las partículas suspendidas en el medio fluirán a lo largo del medio, a una cierta velocidad con el impacto de la superficie de la pieza de trabajo de microcorte (Fig. 1).

Boceto de pieza de trabajo de corte abrasivo. Todas las cifras tratan sobre el efecto de la dirección de impacto en el proceso de corte nanométrico abrasivo con dinámica molecular. La figura 1 es el boceto de la pieza de trabajo de corte abrasivo. En el proceso de pulido de flujo abrasivo, las partículas suspendidas en el medio fluirán a lo largo del medio a una cierta velocidad con el impacto de la superficie de la pieza de trabajo de microcorte

Como la forma de los granos abrasivos no es regular, tienen ciertos bordes y esquinas que actúan sobre la superficie de la pieza de trabajo, similar a la herramienta. Pero el proceso de corte es a escala atómica, lo que obviamente es diferente del proceso de remoción de material. Un corte a nanoescala involucra pocos nanómetros o menos de la superficie del material, pero es muy difícil observar este proceso mediante experimentos. Por tanto, la simulación MD como método de investigación teórica es muy útil para estudiar el proceso de corte nanométrico. La dinámica molecular como técnica de simulación por computadora, que utiliza un método de mecánica estadística basada en el tiempo para estudiar la interrelación de los átomos para la predicción y el análisis de condiciones. Esta también es una herramienta poderosa para simular y comprender los procesos de remoción de materiales. En la literatura existen numerosos estudios sobre la MD como herramienta para investigar el mecanizado de precisión. Oluwajobi y Chen han realizado un trabajo extenso en la simulación MD del mecanizado a nanoescala de cobre [7]. En sus estudios, investigaron varios parámetros para la nanomáquina, como la profundidad mínima de corte, la geometría y el potencial interatómico [8]. Además, los resultados de las simulaciones MD también han tenido éxito en el pasado para abordar varios problemas relacionados con el proceso de corte nanométrico de materiales frágiles como el silicio [9]. Komanduri y col. realizó una simulación MD para el corte nanométrico de monocristales de silicio puro sin defectos, utilizando el potencial de Tersoff. Estudiaron los efectos del ángulo de ataque, el ancho de corte, la profundidad de corte y el ángulo de separación sobre la eliminación de material y la generación de superficie [10]. Goel y col. investigó los aspectos atomísticos de la respuesta dúctil del SiC durante el proceso de corte nanométrico. Descubrieron la presencia de una transición de orden-desorden sp3-sp2 que finalmente resultó en la grafitización del diamante [11]. Cai y col. utilizó MD para estudiar el corte de silicio en modo dúctil a nanoescala. Informaron sobre el filo de la herramienta y sus efectos sobre el esfuerzo cortante en el material de la pieza de trabajo [12]. Arafin y col. ha discutido el efecto del radio del filo en el corte en modo dúctil a nanoescala de obleas de silicio [13]. Varios otros investigadores también han destacado las diferentes condiciones en la nanomáquina de silicio utilizando simulaciones MD. Las investigaciones consisten en fuerzas de corte, profundidad de corte, temperatura, esfuerzo cortante y otros parámetros. Sin embargo, hay una falta de validaciones experimentales adecuadas en esta área. Qihong Fang y col. estudiaron el mecanismo de interacción de las dislocaciones en diferentes materiales heterogéneos con diferentes escalas, y la dislocación y la relación entre la tenacidad del material y el daño por fractura. Usan simulaciones de dinámica molecular para estudiar la nanoindentación en tres estructuras cristalinas diferentes, incluido el cobre monocristalino, policristalino y policristalino nanotwinned. Con el aumento de la tasa de rayado, la fuerza de rayado y la temperatura de la pieza de trabajo aumentan continuamente debido a la deformación plástica severa y al gran volumen de viruta, lo que resulta en deslizamiento por dislocación, deslizamiento GB y hermanamiento / destwinning [14, 15].

Métodos / Experimental

En el experimento de pulido con flujo abrasivo, la pieza de trabajo se cortó generalmente con abrasivo SiC. Una vez establecido el modelo de granos abrasivos de SiC, el software Lammps llevó a cabo la simulación de dinámica molecular de la pieza de trabajo. Se construyó el modelo de cobre monocristalino de corte abrasivo de dos SiC con diferentes ángulos. En la Fig. 2 se muestra un modelo de simulación de un cobre monocristalino de corte por choque de granos abrasivos de SiC.

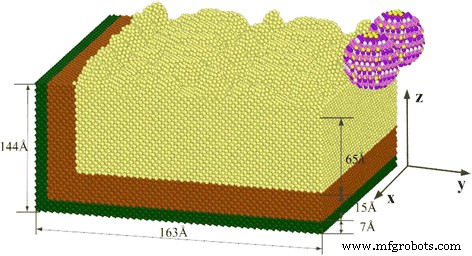
Modelo de simulación de cobre monocristalino de corte abrasivo de SiC. La Figura 2 es sobre el modelo de simulación de cobre monocristalino de corte abrasivo de SiC; construimos dos abrasivos de SiC para cortar cobre monocristalino. En el experimento de pulido con flujo abrasivo, la pieza de trabajo se cortó generalmente con abrasivo SiC. Después de la construcción del modelo de abrasivo SiC, se llevó a cabo la simulación de dinámica molecular de la pieza de trabajo. Se construyó el modelo de dos cobre monocristalino de corte abrasivo de SiC con diferentes ángulos

El tamaño del modelo se muestra en la Fig. 2, mientras que el número de átomos simulados fue de 159 020. El radio abrasivo es 15 Å, el número total de átomos de C y átomos de Si en los granos abrasivos es 1406. Y el número de átomos de carbono y silicio fue 681 y 725, respectivamente. El número de paso de relajación se establece en 10,000 pasos para el conjunto de equilibrio simulado, los pasos de simulación de colisión en 100,000 pasos de corte, cada paso de la simulación fue 0.001 ps, simulación de corte, las partículas abrasivas de SiC en la dirección de corte velocidad de 80 m / s. Los granos de valor de análisis AFM chocan con la pieza de trabajo de micromecanizado durante el pulido, granos abrasivos de SiC para explorar la dinámica de colisión molecular en diferentes ángulos del proceso de corte. En el proceso de corte de flujo abrasivo, la fuerza de corte aumenta a medida que aumenta la velocidad de corte, y el tamaño de la fuerza de corte afecta directamente el efecto de corte. Por lo tanto, la elección de una velocidad de corte razonable tiene un impacto importante en la calidad del corte. Para lograr un corte de alta calidad, elegimos la velocidad de corte de 80 m / s, porque produce la fuerza de corte que puede destruir rápidamente la interacción entre los átomos de la pieza de trabajo [16].

En simulaciones de dinámica molecular a baja velocidad de corte, como 10 m / s, los mapas de desplazamiento atómico y el patrón de cómo la fuerza de corte de las partículas abrasivas de carburo de silicio y los ángulos de corte varían con el tamaño del paso de simulación, como se muestra en las Figs. 3 y 4. Debido a que la velocidad de corte es demasiado pequeña, la fuerza de corte también es inadecuada, lo que resulta en una deformación y dislocación mucho menor de la celosía. En general, la eficiencia de corte es baja y la calidad de corte es relativamente mala. Por el contrario, cuando la velocidad de corte es de hasta 80 m / s en un experimento microscópico, los enlaces químicos entre los átomos de cobre se pueden romper de manera rápida y efectiva, para lograr el objetivo de un corte instantáneo de alta calidad. Por lo tanto, después de un análisis exhaustivo, la velocidad de corte de 80 m / s es razonable para la simulación.

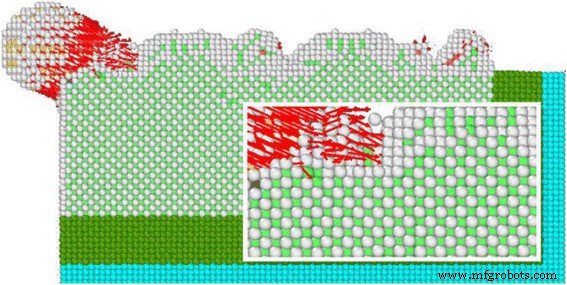
Desplazamiento atómico de baja velocidad

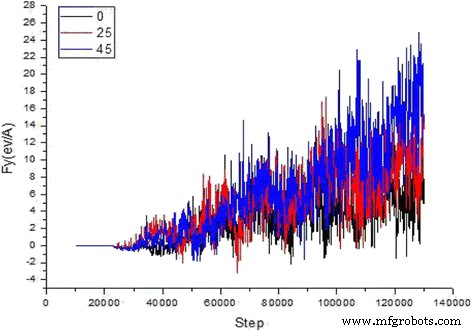
La relación entre la fuerza de corte, el ángulo de corte y el paso de simulación

Para simular la viabilidad y credibilidad, elegimos una función de potencial empírica razonable para considerar los potenciales interatómicos de los átomos. Según los diferentes objetos, podemos dividir la función potencial en función potencial par y función potencial de muchos cuerpos. Los dos modelos entre cobre monocristalino y granos abrasivos describen los potenciales interatómicos de átomos entre ellos por potencial Morse [17], el potencial EAM se usa para describir los potenciales interatómicos de átomos entre átomos de cobre [18,19,20], y el La interacción entre partículas de SiC se describe utilizando el potencial de Tersoff [21].

Durante el proceso de pulido, la dirección de colisión de los granos abrasivos en el medio es aleatoria; sus trayectorias no se encuentran exactamente a lo largo de la superficie de la pieza de trabajo. Durante el proceso de microcorte, la dirección de corte de los granos abrasivos no siempre es ortogonal al material de la pieza de trabajo. El ángulo de corte se refiere al grado del ángulo entre la dirección de corte del grano abrasivo y el plano horizontal. Es positivo cuando las partículas se acercan a la superficie de la pieza de trabajo. El esquema del ángulo de corte se muestra en la Fig. 5.

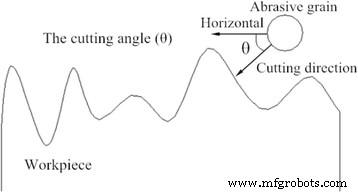
El boceto del ángulo de corte. La figura 5 es el esquema de los diferentes ángulos de corte cuando se cortan los granos abrasivos. Grano abrasivo de diferentes direcciones cortando el material de la pieza de trabajo, el material tendrá el rendimiento y la calidad de procesamiento será diferente

En este estudio, la simulación MD se emplea para simular multi-abrasivos con diferente dirección de impacto del cobre monocristalino cortado. Como se muestra en la Fig. 5, el ángulo de corte está entre 0 ° y 45 ° mientras que la superficie de la pieza de cobre es rugosa.

Resultados y discusión

Análisis de la colisión de la mecánica de corte abrasivo de SiC

El impacto del abrasivo de carburo de silicio en el corte de material de cobre monocristalino se logra mediante la destrucción de la estructura reticular del monocristal de material de cobre. Durante la ruptura, las interacciones entre los átomos de cobre, el esfuerzo cortante impuesto por los átomos de C, Si de las partículas abrasivas de SiC en los átomos de Cu del material de la pieza de trabajo se identificó como la fuerza de corte, que es un parámetro físico importante por el hecho de que la fuerza de corte refleja profundamente el proceso de eliminación del material de la pieza de trabajo de cobre monocristalino. Como se mencionó anteriormente, existe una gran diferencia entre la fuerza de corte micro y macro. Generalmente, la fuerza de macrocorte es la suma de la fuerza de corte y de rectificado, mientras que en el microcorte, la fuerza de corte es generada por las interacciones entre los granos abrasivos y los átomos de la pieza de trabajo.

En la Fig. 6, mostramos los cambios del esfuerzo cortante de los granos abrasivos en varias direcciones, el efecto del esfuerzo cortante en diferentes direcciones y la distribución de las fuerzas de corte a lo largo de diferentes ángulos de corte.

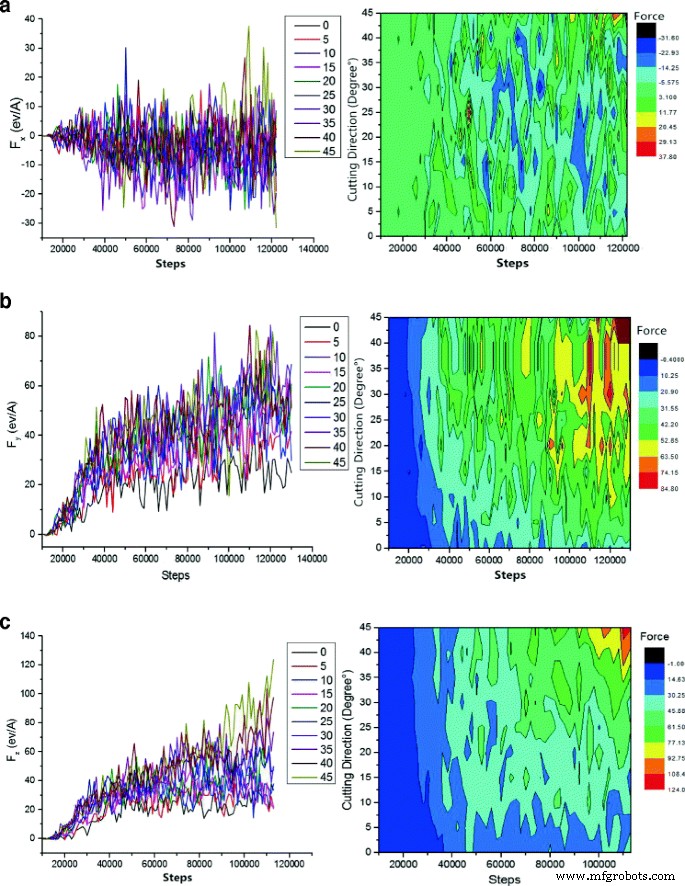
Cómo el ángulo de corte y el tamaño del paso de simulación afectan la fuerza de corte. La Figura 6 muestra la fuerza de corte abrasiva de SiC y el ángulo de corte y el diagrama de pasos de simulación, con el aumento de la profundidad de corte, el número de estructura cristalina de destrucción aumenta, el valor máximo de la fluctuación de la fuerza de corte también aumenta. un [100] dirección de la fuerza de corte. b [010] dirección de la fuerza de corte. c [001] dirección de la fuerza de corte

Los granos abrasivos de carburo de silicio cortan e impactan en material de cobre monocristalino en diferentes ángulos de borde como [010] y [100]. Las fuerzas de corte en las direcciones [001] y [010] fueron fuerzas de corte. En la simulación adicional, la profundidad de corte aumentó gradualmente, lo que ha elevado de manera persistente las fuerzas de corte a lo largo de la dirección [001] y [010]. Sin embargo, hasta cierto límite, estas fuerzas fluctuaron como se puede ver en la Fig. 6. Cuando las partículas abrasivas se movieron hacia los materiales de la pieza de trabajo, cambió totalmente la interacción (de atracción a repulsión) entre los átomos de cobre más externos y los átomos. de SiC (Si y C). Inicialmente, mientras se trituraba el material de la pieza de trabajo, las fuerzas de corte eran inadecuadas debido a la presencia de fuerzas repulsivas de átomos de cobre. Para el proceso de acabado, las fuerzas de corte deben ser lo suficientemente altas para que los granos abrasivos puedan romper fácilmente los enlaces químicos en los átomos de cobre para moverse libremente. Además, el incremento de la profundidad de corte tiene relaciones directas con las interacciones atómicas. Cuando los átomos comenzaron a acumularse, la fuerza de corte aumenta constantemente hasta que las partículas abrasivas ingresan a la pieza de trabajo, lo que requiere una fuerza de corte en estado estable. En esta etapa relativamente estable, la fluctuación de la fuerza de corte se sometió al grado de deformación de la red, reconstrucción de la red, cambio de fase amorfa y generación de virutas. A medida que los granos abrasivos marcharon a lo largo de la dirección de corte, se suministró una fuerza externa sobre el átomo de cobre en la red de FCC, lo que resultó en desplazamientos de los átomos de cobre. Este desplazamiento colapsa la celosía de FCC y la transforma en una nueva estructura de celosía que tiene dislocación. También se observa una situación similar en la fuerza de corte. No existe una correlación lineal positiva entre la fuerza de corte a lo largo de la dirección de [010] y el ángulo de colisión de las partículas. En la colisión con 0 °, 5 °, 10 ° y más allá, la fuerza en la dirección [010] fue menor y menos fluctuante que en otras direcciones de corte. Cortar en un ángulo más pequeño, básicamente elimina las rebabas, ya que la rebaba se puede definir en un rango de altura de 3,5 ~ 15 Å. Al comparar estas direcciones entre sí, si la profundidad de corte es relativamente menor, el daño y la deformación de la estructura cristalina serán moderados. Por lo tanto, en todo el proceso de corte, la fuerza cortante a lo largo de la dirección [010] se mantuvo más pequeña, como se muestra en el gráfico de curva de la Fig. 6b. En la última etapa de la simulación, la fuerza de corte alcanzó el mínimo de 0 °. También se encuentra que la fuerza de corte tiene relación directa con el ángulo como se muestra en la Fig. 6c, lo que puede atribuirse al hecho de que cuando la velocidad de las partículas alcanza 80 m / s, se logra un ángulo de corte mayor. Por otro lado, en el mismo paso de simulación, cuanto mayor es la velocidad del componente a lo largo de la dirección [001], mayor es el ángulo, las partículas más profundas se cortan y más redes atómicas se destruyen. Sin embargo, hubo una correlación positiva entre el ángulo de corte y la fuerza de corte. Cuando los granos se movían a lo largo de la dirección [100], las fricciones entre los átomos de C, Si y Cu eran la fuente de la fuerza de corte. Entonces, la fuerza de corte no mostró una tendencia de aumento gradual. Sin embargo, en la simulación adicional, la fuerza de corte aumentó y fluctuó, lo que estuvo estrechamente relacionado con la deformación y reconstrucción de la celosía, así como con la generación de transición de fase estructural amorfa. Antes de que las partículas abrasivas pudieran destruirse, se logra la interacción entre los átomos de la pieza de trabajo para eliminar el material, que finalmente ha aumentado la fuerza de corte de manera constante. Al aumentar la fuerza de corte abrasiva, más allá del valor crítico (fuerza de unión del átomo), la red atómica se daña y los enlaces se disocian, lo que da como resultado una estructura amorfa. Al lograr esto, la fuerza de corte cayó a un valor relativamente bajo. Las fluctuaciones de la fuerza de corte aparecieron continuamente durante todo el proceso de mecanizado de flujo abrasivo, lo que se debe al aumento de la profundidad de corte, y se produjo una mayor destrucción de la estructura cristalina. Entonces, se concluye que en esta etapa, el valor máximo de la fluctuación de la fuerza de corte fue mayor. Como se muestra en la Fig. 6b, la región roja ocupó un área más grande durante la última etapa de la simulación, lo que indica que la fuerza de corte se elevó notablemente. En el mismo tiempo de simulación, la fuerza de corte fue menor cuando el ángulo de corte era menor de 15 °, lo que significa que se destruyó una pequeña porción de la red cristalina.

Análisis de energía para el proceso de corte por impacto abrasivo de SiC

La energía total termodinámica es la suma de la energía potencial total y la energía cinética total en un sistema, que revela el efecto del trabajo realizado en la pieza de trabajo por los granos abrasivos. La influencia del ángulo de corte en el abrasivo de carburo de silicio sobre el cambio de energía del sistema se muestra en la Fig. 7. En el proceso de corte, los materiales de la pieza de trabajo de cobre monocristalino con granos abrasivos de carburo de silicio, el trabajo realizado por los granos abrasivos sobre el material de la pieza de trabajo actúa en dos maneras; una parte se convierte en energía cinética que aumenta el calor de los átomos de cobre monocristalino el contacto con las partículas de carburo de silicio funciona el pulido, la otra parte se convierte en energía potencial que permite cambios en la estructura interna de la pieza de cobre monocristalino, la deformación de la red y la liberación de energía de la red.

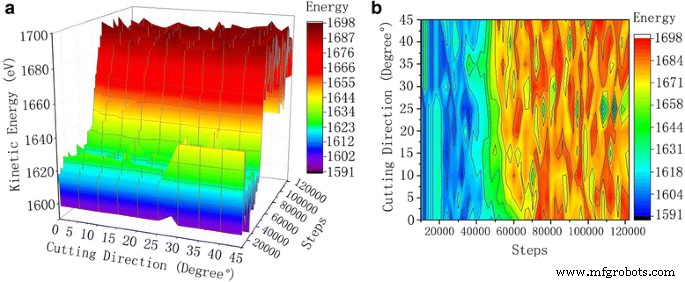
Curva de energía cinética de los átomos de la pieza. La figura 7 es la curva de energía cinética de los diferentes ángulos de corte durante el proceso de corte. Con el aumento en el número de pasos de simulación, la energía cinética de los átomos fluctúa en un rango bajo y luego en un rango más alto dentro de las fluctuaciones. un Curva 3D. b Contorno

En el proceso de corte de grano abrasivo de una pieza de trabajo de cobre monocristalino, la energía cinética del sistema está estrechamente relacionada con el trabajo realizado por los abrasivos de SiC sobre el material de la pieza de trabajo. Calculando la velocidad de las partículas en el sistema en cada momento, se puede calcular la energía cinética total del sistema:

$$ K =\ sum \ limits_ {i =1} ^ N \ frac {1} {2} {m} _i \ left ({v} _ {\ mathrm {ix}} ^ 2+ {v} _ {\ mathrm {iy}} ^ 2+ {v} _ {\ mathrm {iz}} ^ 2 \ right) $$ (1)

En la fórmula, \ ({v} _ {\ mathrm {ix}} ^ 2 \), \ ({v} _ {\ mathrm {iy}} ^ 2 \) y \ ({v} _ {\ mathrm {iz}} ^ 2 \) representan el componente de velocidad x , años , z átomos de dirección, respectivamente.

La curva cinética de la Fig. 7 nos llevó a concluir que al incrementar los pasos de simulación, inicialmente la energía cinética de los átomos fluctúa en un rango bajo y luego en un rango más alto. Con el movimiento de los granos abrasivos, se encuentra una interacción repulsiva de largo alcance entre los átomos de cobre más externos y los átomos de Si, C (SiC). Los átomos de cobre en la pieza de trabajo comienzan a recibir energía cinética y se mueven. Cuando las partículas de carburo de silicio entran en contacto con el monocristal de cobre, la temperatura atómica de la región de contacto aumenta, lo que aumenta el movimiento térmico atómico. Cuando el corte es estable, la energía cinética de los átomos de cobre en el material se transmite y se transforma en un patrón de equilibrio dinámico, y la energía cinética de los átomos fluctúa en un rango alto.

El análisis de la energía cinética nos llevó a concluir que durante el proceso de corte, cuando las partículas comienzan a entrar en contacto con la pieza de trabajo, los átomos en la región extruida sufren una deformación reticular, las coordenadas atómicas cambian y el desplazamiento cambia con la energía cinética. Con las partículas abrasivas entrando en el cobre monocristalino, el valor máximo de la energía cinética de la pieza de trabajo de cobre monocristalino aparece cuando la pieza de trabajo entra completamente en la pieza de trabajo. Porque la energía cinética y la energía potencial de las partículas abrasivas simplemente se transforman mutuamente. Sin embargo, la energía de todo el sistema no cambiará, a excepción de las partículas en movimiento, que entran en la pieza de trabajo. Además, el movimiento de las partículas de carburo de silicio obliga a los átomos de la pieza a moverse simultáneamente con ellos. El calor generado durante la fricción atómica es liberado por la energía cinética y la energía de deformación liberada debido al movimiento de dislocación.

La conversión entre calor y energía cinética se calcula mediante la siguiente fórmula:

$$ \ frac {1} {2} {\ sum} _i {m} _i {v} _i ^ 2 =\ frac {3} {2} {nk} _B {T} _i $$ (2)

En la fórmula, n es el número de átomos; vi representa la velocidad instantánea; k _B es la constante de Boltzmann y T _i es la temperatura de los átomos.

La fuerza de corte aumenta la temperatura atómica del área donde el abrasivo entra en contacto con el material de la pieza de trabajo. Al considerar el movimiento térmico del átomo y la energía cinética de los átomos, la energía cinética de los átomos de cobre aumenta parcialmente. El sistema simulado se ajusta al conjunto canónico; la temperatura general del sistema fluctúa en un cierto rango. El calor producido durante el corte de partículas abrasivas se transfiere rápidamente a la capa de átomos de temperatura constante, por lo que la energía cinética general del sistema cambia muy poco.

Como puede verse en la curva de energía potencial de la Fig. 8, al aumentar el número de pasos de simulación, la energía potencial entre el monocristal de átomos de cobre en la pieza de trabajo también tiende a aumentar. Cuando el abrasivo de carburo de silicio entra en contacto con el monocristal de la pieza de trabajo de cobre desde el inicio hasta el corte completamente estable, el material de la pieza de trabajo se deforma gradualmente y los átomos de cobre se desplazan, lo que conduce a la distorsión de la red cristalina en el cristal. Esto también da como resultado un campo de tensión elástica, donde aumenta la energía de deformación. Cuando la energía de deformación no es suficiente para reorganizar los átomos materiales, se produce la dislocación de los átomos, lo que aumenta la energía total del sistema. En contraste con las curvas de potencial de 0 ° a 45 °, podemos ver una consistencia en el movimiento térmico de los átomos a temperatura constante. No existe una relación significativa entre la energía cinética atómica y el ángulo de corte de los granos abrasivos de SiC. La energía cinética de los átomos está estrechamente relacionada con el movimiento térmico de los átomos. Sin embargo, el cambio de energía potencial y energía total está obviamente relacionado con el ángulo de corte de las partículas abrasivas de SiC. La magnitud de la energía potencial atómica aumenta con el aumento del ángulo de corte. Cuando el ángulo de corte está entre 0 ° y 20 °, se observa un cambio obvio en la energía potencial. Sin embargo, cuando el ángulo de corte está entre 25 ° y 45 °, la energía potencial permanece como tal, y las curvas de energía potencial general son del ángulo de corte de 0 ° a 20 °. Como se muestra en la Fig. 9, la tendencia de la energía total es similar a la de la curva de energía potencial. Los valores de energía total de todos los ángulos de corte están muy próximos entre sí. Esto se debe a que la energía total es igual a la energía potencial y la energía cinética del sistema, mientras que la energía cinética no cambia al ritmo del ángulo de corte durante el proceso de corte. El cambio en la energía cinética de la pieza de trabajo es muy bajo con diferentes ángulos de corte. Por tanto, la curva de cambio de la energía potencial es similar a la curva de la energía total. Comparando los diagramas de desplazamiento atómico de la Fig.9, se puede encontrar que bajo la misma condición de corte, la profundidad de corte en la pieza de trabajo de cobre monocristalino es mayor cuando el ángulo de corte está entre 25 ° y 45 °, lo que puede atribuirse al aumento del desplazamiento. de átomos de cobre. A lo largo de la dirección de las partículas de SiC, se generan más daños atómicos en la red y dislocaciones. La energía de deformación producida durante este tiempo es mayor, lo que da como resultado una curva de cambio de energía potencial alta y una curva de cambio de energía total de los átomos de la pieza de trabajo.

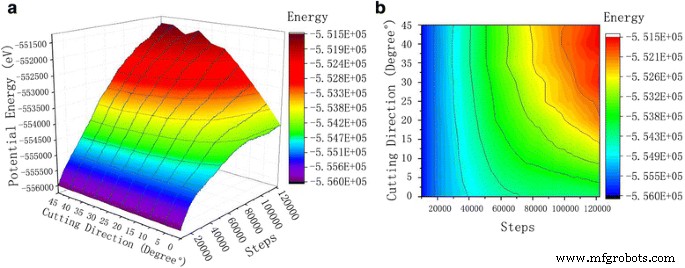
Curva de energía potencial de la pieza. La figura 8 es un gráfico de las variaciones de energía potencial en diferentes ángulos de corte durante el proceso de corte. Con el aumento en el número de pasos para la simulación, el potencial entre los átomos de cobre monocristalinos exhibidos en la pieza de trabajo tiende a aumentar. un Curva 3D. b Contorno

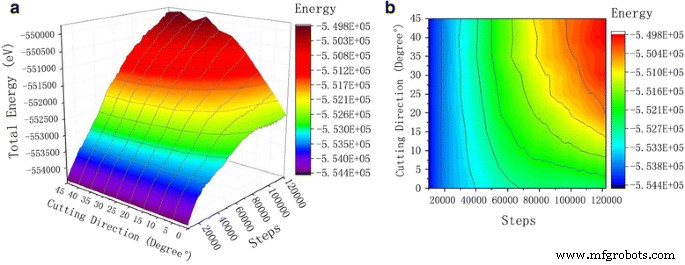
Curva de energía total. La figura 9 muestra la curva de energía total. Durante el proceso de corte de SiC de la pieza de trabajo de cobre monocristalino, el efecto de los granos abrasivos en la pieza de trabajo se manifiesta de dos formas:parte de la cual se convierte en energía cinética, el calor atómico aumenta y la energía cinética local aumenta al pulir. el área de unión de la pieza de trabajo de cobre monocristalino y las partículas SIC; la otra parte se convierte en energía potencial, la estructura interna de la pieza de trabajo de cobre monocristalino se cambia, la celosía se deforma y la energía de la celosía se libera y se transforma en energía potencial. un Curva 3D. b Contorno

Análisis del desplazamiento atómico en el proceso de corte de colisión de partículas abrasivas de SiC

En el proceso de corte del material de la pieza de trabajo en varios ángulos, los granos abrasivos se mueven a lo largo de la dirección de corte, lo que obliga a los átomos de cobre de la pieza de trabajo a moverse. A partir del análisis de la dirección de movimiento de la pieza de trabajo, se aclara por completo el efecto de los granos abrasivos en el material de la pieza de trabajo, cómo se forma la viruta y la eliminación del material. De acuerdo con el método de análisis del ángulo de enlace, propuesto por Ackland-Jones, las diferentes estructuras de celosía atómica se marcan con colores diversificados, con fines de observación y análisis. El plano ZOY se selecciona para observar el proceso de corte de una partícula de SiC individual, y el diagrama de desplazamiento atómico del área de corte se agranda, como se puede ver en la Fig. 10.

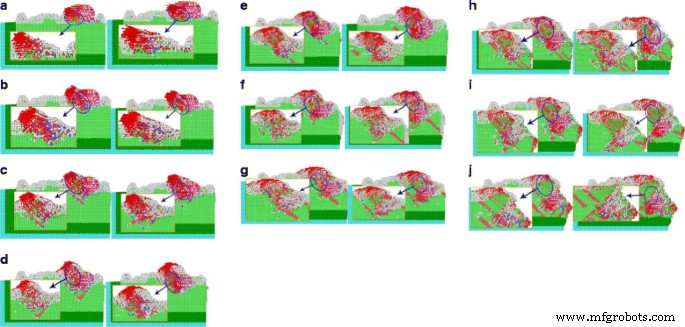
Diferentes ángulos de corte provocan desplazamientos atómicos. La figura 10 describe los desplazamientos atómicos de diferentes ángulos de corte. Cuando las partículas abrasivas monocristalinas de SiC chocan con la pieza de trabajo cortando cobre en diferentes direcciones, con los granos abrasivos de SiC cortados, la profundidad de corte aumenta, ya que la velocidad de la dirección de corte es de 80 m / s, la dirección [001] La velocidad de movimiento es v _z =0.8 ∗ sin θ , al aumentar la profundidad de corte del ángulo de corte, en el mismo ángulo de corte aumenta los pasos de simulación, la profundidad de corte es grande al mismo tiempo. un Desplazamiento de 0 °. b Desplazamientos de 5 °. c Desplazamiento de 10 °. d Desplazamiento de 15 °. e Desplazamiento de 20 °. f Desplazamiento de 25 °. g Desplazamiento de 30 °. h Desplazamiento de 35 °. yo Desplazamiento de 40 °. j Desplazamiento de 45 °. (color atómico: Estructura de HCP, Estructura BCC, Configuración de FCC como una estructura amorfa blanca)

Cuando las partículas abrasivas monocristalinas de SiC chocan con la pieza de trabajo que corta el cobre en diferentes direcciones, la profundidad de corte aumenta a lo largo del proceso. La velocidad de la dirección de corte es 80 m / s, donde la velocidad del componente en la dirección [001] es v _z =0.8 ^∗ pecado θ . At the same simulation step, cutting depth increases with increasing the cutting angle. As shown in Fig. 10, there is an atomic position shift in both of the surface and interior of the workpiece material, contacting with the abrasive grains, where atoms of different lattice types are arranged and doped with each other. Due to the movement of these abrasive particles, the copper atoms accumulated at the tip of the abrasive grains, which results no cracks during abrasive particles cutting. It can be seen that the material removal mode of the abrasive particles is plastic deformation. At the same time, due to abrasive cutting, the atoms displacement in single crystal copper increases from 15° to 45°.

The number of the workpiece atoms along the abrasive grain motion direction also increases, and the atomic displacement is perpendicular to the direction of abrasive cutting. This part of the atomic displacement is due to that of the abrasive particles, change the cutting action to the extrusion upon the workpiece atoms. At cutting angle, the abrasive particles is between 0° and 10°, while the cutting depth is smaller than those of the 15° to 45°. Abrasive particles are performing mainly the cutting function, the extrusion of the workpiece atoms is marginal, and the number of atoms is small whose displacement direction is perpendicular to the direction of the abrasive grain motion. With the repeated cutting on the workpiece surface by numerous abrasive particles, the abrasive particles having large cutting angle produce deep pits on the workpiece material during the whole cutting process, while ones following smaller cutting angles will continue cutting along the cutting mark produced by the former. Under the combined action, the workpiece material is cut to a certain depth (micro-cutting) followed by whole abrasive flow polishing.

Dislocation Collision Analysis for SiC Abrasive Cutting

Dislocation is a special arrangement of atoms in crystal along certain crystal surface and crystal direction, or a boundary between the slip zone and the non-slip zone on the slip surface. Dislocation can be divided into edge dislocation, spiral dislocation, and mixed dislocation, among which mixed dislocation is most common. In the process of abrasive particle cutting, the single crystal copper workpiece is plastically deformed, the atoms move, and the crystal lattice breaks and reconstructs, which results in a large number of dislocations. The analysis for dislocation and bond angles at different incidence angles is shown in Fig. 10. In the simulation model of abrasive flow simulation, two abrasive particles are used for cutting the workpiece material. For ease of analysis, the generation and change of different dislocation lines in single crystal copper material, during cutting process and the different lattice structures in the cutting part are analyzed in the view of one single SiC particle on the YOZ surface, as shown in Fig. 11.

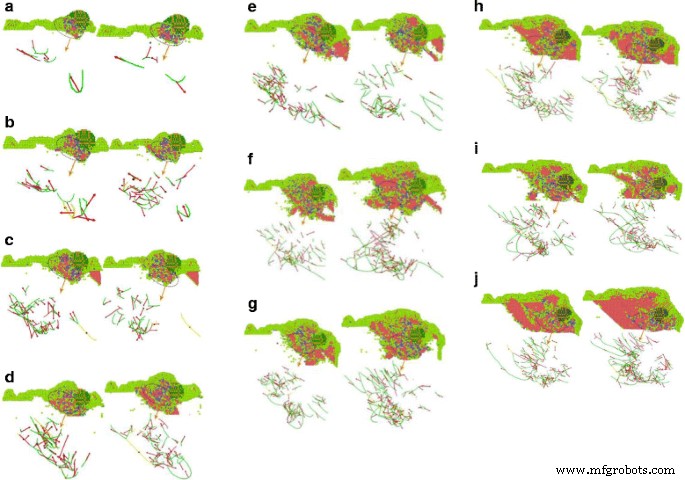
Different angles-bond angle dislocation line charts. Figure 11 represents the cutting dislocation line and the bond angle. As the repeated cuttings on the workpiece surface are done by the numerous abrasive particles during the polishing process, in the entire cutting process, the abrasive particles with larger cutting angle produce bigger pits, while the following abrasive particles with smaller cutting angles continue to polish along the cutting trace. Therefore, certain depth is done on the workpiece material and the whole micro-cutting of abrasive flow polishing is achieved. un Dislocation lines with 0° cutting angles. b Dislocation lines with 5° cutting angles. c Dislocation lines with 10° cutting angles. d Dislocation lines with 15° cutting angles. e Dislocation lines with 20° cutting angles. f Dislocation lines with 25° cutting angles. g Dislocation lines with 30° cutting angles. h Dislocation lines with 35° cutting angles. i Dislocation lines with 40° cutting angles. j Dislocation lines with 45° cutting angles. (Note:the upper part of the key angle analysis, the figure in the atomic color: HCP BCC Amorphous structure Abrasive grain; the lower part of the dislocation line diagram, the figure dislocation line color: Stair-rod, Shockley, Hirth, Perect, Frank, Burgers vectors)

Key angle analysis diagram of each cutting angle is shown in Fig. 11, where the sample from the interior workpiece simulation at time 60 and 70 ps, the atoms are colored individually according to different arrangement of atoms through BAD technology. To facilitate the analysis of the lattice changes in the cutting part, atoms of the FCC structure in the workpiece material are removed. By DXA techniques, different types of dislocations are marked in diverse colors:red arrow indicates the Burgers vector (Burgers vectors), green for Shockley partial dislocations (Shockley), light blue for the Frank partial dislocations (Frank), pink pole position for the pressure error (Stair-rod), and blue for the whole dislocation (Perfect).

As can be observed from the analysis of the bond angle portion in Fig. 11, a large number of dislocations and lattice deformations occurred under the impact of external cutting forces. The bond angle analysis shows that the internal HCP structure of the workpiece appears more clearly with increasing of cutting angle. On further simulations, the structure of HCP increases gradually. The silicon carbide particles continuously cut and squeeze the workpiece material at 80 m/s speed, resulting in a phase transition from the FCC structure to the HCP structure. During this phase transition, the atomic strain of the workpiece continues to increase. However, when the stress state of atoms of the workpiece has exceeded the threshold of thermodynamic phase transition, it turns to metastable state. As the strain increases, the HCP phase begins to nucleate and grow spontaneously, and the FCC lattice of copper undergoes absolute destabilization, which induces a sudden change in mechanical quantities. As the kinetic energy of the atom is directly related to the atomic temperature (formula 1), there is a saltatory augment in the kinetic energy change curve, as can be seen from Fig. 7. This is due to high strain energy, accumulated in the single crystal copper workpiece before the nucleation of HCP. The HCP structure increases the system temperature through metastable nucleation and partial stress release. Due to the abrasive cutting and extrusion, bonds of copper atoms in workpiece material break down which results in disorder. The original regular lattice structure is broken, where the partial copper atoms gradually change into disorder and form an amorphous structure. It can be seen from the bond angle analysis diagram that (Fig. 11) atoms with relatively disordered displacement tend to form amorphous structures at 60 and 70 ps, which is because of silicon carbide abrasive particles. At the same time, many atoms with the same displacement direction are transformed into HCP structures. Meanwhile, the particles shear downward and the atomic structure is rearranged due to the displacement of atoms in the original amorphous structure, results an amorphous structure of HCP. Atoms that have already been transformed into HCP structures, even before the next cut stage, change back into amorphous structure. As the cutting depth increases, the number of amorphous atoms near the abrasive particles also increases.

When the FCC crystal structure undergoes cutting by abrasive particles, a shear stress generates in atoms, which results in the displacement of atoms in the lattice and the arrangement of various lattice structures. In moving the atoms of workpiece, the rigid displacements of the atoms produce dislocations, also called as dislocation lines (Fig. 11). Dislocation line can be termed as the boundary between the slip zone and the non-slip zone, on the slip surface. According to the relation between the dislocation and the PATS vector, dislocation is parallel to the PATS vector, called the screw dislocations. The vertical ones are edge dislocations, and the mixed dislocations are neither parallel nor vertical. In Fig. 11, most of the dislocation lines are neither parallel nor vertical to PATS vectors, which are typical mixed dislocations. In the cutting process of abrasive particles, the dislocation line changes, moves and grows around the abrasive particles. The closer the particle, the greater the density of the dislocation line. Dislocation lines are also very dense, when the arrangement of atoms is complicated. The abrasive particles marked as orange, produce a large amount of HCP, BCC, and amorphous structures around them, which interlace and blend with each other to form dislocations that increases the internal energy of the crystals. When atoms arrange their self just like shown in Fig. 12b, possess maximum potential energy. While for the arrangement, shown in Fig. 12a–b, the atoms situate at the lowest potential energy position. The number of dislocation lines is directly related to the magnitude of strain energy of the crystal. The total strain energy of the unit length dislocation can be measured with the given formula:

$$ W=\alpha {Gb}^2 $$ (3)

Schematic view of dislocation changes. Dislocation is a special arrangement of atoms in crystals. It is the crystal in the atomic arrangement along a certain crystal face and crystal orientation occurred in a certain wrong line, and it is the boundary of the slip surface within the area where the slip has occurred and the area with no slip has occurred. In Fig. 12a –c , the relative displacement of the rigidity of the upper atom and the underlying atom produce dislocations, the upper atom belongs to the sliding region, and the lower atoms belong to the non-slip region, they are in the slip surface of the intersection line which is called dislocation line, that is, dislocation. Figure 12 is the process of dislocation generation and development

Where, α is the geometric factor (type dislocations, dislocation density) parameter related to, and generally 0.5 ~ 1.0; G is the shear modulus, and b is the slippage distance.

When the workpiece material is being cut, particles break the atomic arrangement and the lattice reconstructs, which constitutes, macroscopically, the plastic deformation of the workpiece material. In the process of plastic deformation, the dislocation was supposed to escape from the crystal and decrease the dislocation density. However, this dislocation density increases due to dislocation propagation. There are many ways of dislocation multiplication and the main one is the Frank–Reed dislocation source theory, of which the growth mechanism is shown in Fig. 11. As illustrated in Fig. 11, the density of the dislocation line increases markedly from 60 to 70 ps when the cutting simulation proceeds, change both the number and shape of dislocation lines in accordance with Frank–Reed dislocation source theory. At simulation time of 60 ps, there are many long Shockley dislocations. But after another 10 ps simulating, the long Shockley dislocation line becomes less and shorter. The original straight dislocation lines turn into bent, which is especially evident near the abrasive grains. From formula 3, the strain energy of the dislocation is proportional to b ² . From the viewpoint of energy, the dislocations with the smallest b in the crystal should be most stable with low energy; however, dislocations with larger b will break down into ones. In addition, the energy of the dislocation is valued by the unit length of the dislocation line. Given the shortest line between two points is the straight, the strain energy of straight dislocation is lower than that of the bent one, means straight dislocations are more stable. Frank–Reed dislocation source theory argued that the long dislocation line becomes shorter and breaks down into smaller dislocations, thus decreasing the strain energy of the crystal.

Analysis for Friction Coefficient Between Workpiece Surface and Abrasive Particles

To quantitatively disclose mechanical properties and surface effect of SiC abrasive cutting single crystal copper material, the tangential force ([010] direction) and normal force ([001]direction) on the cutting surface are further analyzed. The friction coefficient can be defined as the ratio of the tangential force to the normal force, with the formula below:

$$ f=\frac{F_y}{F_z} $$ (4)

Figure 13 shows the variation of friction coefficient along different cutting angles during abrasive cutting. The change of friction coefficient can be divided into two periods. Period I, when the cutting distance is less than half of the size of the abrasive particle, the friction coefficient fluctuates violently in certain range due to surface effect of the material; while in period II, all the friction coefficients fluctuate in very small range, and the friction coefficients remains steady state at different angles. However, at cutting angle of 5°, there is a small amount of abnormal fluctuation at the end of simulation. Moreover, in period I, abrasive particles contact the workpiece atoms to the abrasive grains enter into the workpiece of half abrasive diameter (shown in Fig. 13b), the cutting movement distance reaches 7.5 Å. In Fig. 6, the cutting force change curve shows that the tangential force and normal force are in an oscillating phase during period I. Since the friction coefficient can be characterized as the adhesion among atoms in the contact surface and is related to the two atoms contacting with each other, regardless of the cutting mode, which can interpret the phenomenon that change of cutting angle does not cause significant change of friction coefficient, as shown in Fig. 13a.

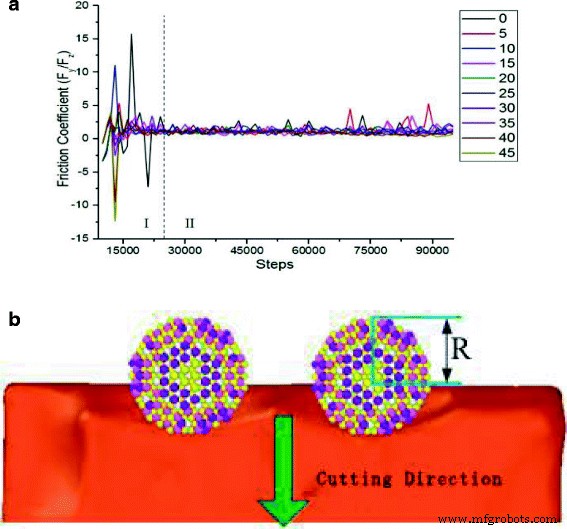
Friction coefficients of different cutting angles. Figure 13 is the changes of the frictional coefficients during SIC particles cutting single crystal copper from different angles. The change in cutting angle did not cause significant changes in friction coefficient. It described two kinds of coefficient of friction in contact with the relevant atoms in the cutting process, regardless of the cutting mode. un Friction coefficient variation curve with cutting angle. b Instantaneous structure when SiC abrasive grains move 7.5 Å

Conclusiones

The micro cutting simulation of single crystal copper by SiC abrasive particles is achieved during abrasive flow polishing. Comprehensive analysis of the SiC abrasive cutting reveals that when SiC abrasive particles cut at angle from 0° to 15°, cutting forces in along Y and Z direction are relatively small and tend to stay steady. A larger cutting angle results more dislocations, which brings about larger grooves damaging of the workpiece material. In the process of cutting, it is necessary to avoid more dislocations, which has an immediate adverse effect on the performance of all aspects of crystal material. Therefore, a cutting angle of 0° is better than other angles. Considering the amount of dislocation produced, or the change of cutting force and energy in the cutting process; cutting with small or medium angles is not only beneficial for improving surface quality but reduce the internal defects.

Efecto catalítico de los clústeres de Pd en la combustión de poli (N-vinil-2-pirrolidona) Nanoconjuntos de ácido 5-aminolevulínico-escualeno para fotodetección y terapia de tumores:estudios in vitro

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias