Estudio de los comportamientos de fricción a nanoescala del grafeno en sustratos de oro utilizando dinámica molecular

Antecedentes

El grafeno es uno de los nuevos materiales prometedores para su aplicación en la electrónica a nanoescala entre una amplia gama de aplicaciones potenciales [1, 2, 3, 4, 5]. En los dispositivos electrónicos reales basados ​​en grafeno, el oro se usa comúnmente para los contactos eléctricos [6]. Por lo tanto, la fricción del sistema de grafeno-oro juega un papel importante en la fabricación eficiente y el funcionamiento confiable de dichos dispositivos de grafeno. Aunque el grafeno ha atraído un gran interés por parte de los investigadores en el campo de la nanotribología debido a sus excelentes propiedades mecánicas [3, 7], las propiedades de fricción del grafeno que se desliza sobre la superficie del oro son poco conocidas. Hasta ahora, muchos estudios tribológicos del grafeno se centran en la fuerza de fricción entre el grafeno y la punta de una sonda de exploración [8,9,10,11,12,13,14]. Por ejemplo, los experimentos de microscopía de fuerza atómica (AFM) de fricción sobre grafito modificado químicamente revelaron un coeficiente de fricción negativo [9]. Los experimentos del microscopio de fuerza de fricción (FFM) de grafeno de pocas capas encontraron que la fricción aumentaba a medida que disminuía el número de capas de grafeno [10, 11]. Estos fenómenos se explican por el efecto de arrugas del grafeno [9,10,11]. Se supone que la fricción entre un copo de grafeno y el grafito se midió cuando la punta arrastraba un copo durante el deslizamiento sobre el grafito [8, 14]. Se encuentra que el movimiento de rotación acoplado al movimiento lateral de las escamas para los sólidos laminares conduce a un aumento de la fricción debido a la reorientación de las escamas en una configuración acorde [15]. Al mismo tiempo, algunos estudiosos también se han dedicado a estudiar la fricción del grafeno y / o el oro utilizando otras técnicas. Se empleó la técnica de microbalanza de cristal de cuarzo (QCM) para estudiar la lubricidad del oro sobre el grafeno [16] y la fricción deslizante de la película de xenón sólida sobre el sustrato de grafeno / Ni (111) [17]. Tanto los experimentos de QCM como las simulaciones de dinámica molecular (MD) muestran que la fricción de una monocapa de Kr inconmensurable sobre Au sigue una ley de fricción viscosa [18, 19]. Se realizan simulaciones MD para explorar la fricción estática de islas de oro bidimensionales y grupos de oro tridimensionales sobre sustrato de grafito [20]. Se encuentra que el grosor del deslizador puede promover la lubricidad debido a la mayor rigidez efectiva de los racimos gruesos. La conmensurabilidad interfacial dependiente del tamaño también fue descubierta por simulaciones MD de átomos de xenón en grafeno y sustrato de Au [21], consistente con las simulaciones de clústeres de criptón y silicio en sustrato de Cu [22], lo que puede explicar la dependencia del tamaño de la fricción estática. Recientemente, se observa la superlubricidad de las nanocintas de grafeno sobre un sustrato de Au (111) a baja temperatura [23]. Kitt y col. midió directamente la fricción del grafeno deslizándose sobre un SiO ₂ sustrato y encontró que los comportamientos de fricción para el grafeno monocapa y bicapa violan la ley de Amontons [24]. En general, como material bidimensional puro, es razonable esperar que el grafeno muestre comportamientos de fricción atípicos para el sistema grafeno-sustrato. Desafortunadamente, todavía falta una investigación detallada de la fricción deslizante del grafeno sobre un sustrato de oro, aunque las propiedades interfaciales entre el grafeno y los metales se han explorado sistemáticamente [25,26,27,28].

Para llenar este vacío, en este artículo, los comportamientos de fricción deslizante de las escamas de grafeno móviles sobre un sustrato de oro monocristalino se estudian a fondo utilizando simulaciones de dinámica molecular (MD). Investigamos los efectos del tamaño de las escamas, la forma de las escamas, el ángulo de rotación relativo entre las escamas y el sustrato y la orientación del cristal del sustrato para aclarar las propiedades de fricción.

Métodos

Método de simulación

Para simular un experimento de AFM en el que un copo de grafeno unido a través de un resorte a una punta se desliza sobre un sustrato de oro [29], establecemos un modelo MD que consiste en un copo de grafeno hecho de N átomos y un sustrato de oro cristalino simple, ver Fig. 1. Las tres capas de átomos en la parte inferior del sustrato se mantienen fijas en el espacio para servir como átomos de límite. Para controlar la temperatura del sistema, se eligen cuatro capas de átomos adyacentes a los átomos del límite en el sustrato como átomos del termostato. Los átomos del termostato se mantienen a una temperatura constante de 300 K mediante el método de escala de velocidad [30]. En este artículo, primero, no consideramos la rotación del grafeno durante el deslizamiento; los átomos en el grafeno solo pueden moverse en el x y z direcciones, pero están restringidas en el y dirección, lo que simplifica las simulaciones. Este es el principal objetivo de este trabajo. Luego, realizamos algunas simulaciones MD sin la restricción de movimiento del grafeno en el y dirección para adaptarse mejor a las condiciones experimentales reales. Los átomos en escamas son arrastrados por un átomo virtual con una velocidad constante a través de un resorte armónico. El resorte paralelo a la superficie del sustrato tiene una rigidez lateral de 10 N / my se utiliza para representar la deformación de la viga en voladizo y el vértice de la punta de un sistema AFM [31]. Se aplica una carga normal constante directamente a los átomos de las escamas en las simulaciones [29, 31]. La escama de grafeno es empujada lateralmente por un átomo virtual a una velocidad constante de 10 m / s. Las ecuaciones de movimiento están integradas con un algoritmo de velocidad-Verlet. El intervalo de tiempo es 1 fs. Los límites son periódicos en x y y direcciones, gratis en la z dirección.

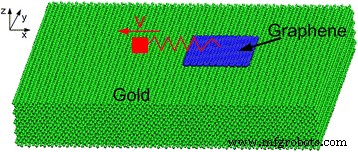
Modelo de simulación del proceso de fricción

Para investigar el efecto de la orientación del cristal del sustrato, realizamos simulaciones MD de fricción por deslizamiento en tres superficies diferentes de los planos Au (111), (001) y (110), respectivamente. Para la superficie Au (111), los sistemas de coordenadas se toman como \ (x- \ left [11 \ overline {2} \ right] \), \ (y- \ left [1 \ overline {1} 0 \ right] \ ) _, y z - [111] y el tamaño es 19,98 × 15,0 × 3,06 nm ³ . Para la superficie Au (001), los sistemas de coordenadas se toman como x - [100], años - [010] y z- [001] y el tamaño del sustrato es 19,99 × 15,1 × 3,06 nm ³ . Para la superficie Au (110), los sistemas de coordenadas se toman como x - [001], \ (y- \ left [1 \ overline {1} 0 \ right] \) _, y z - [110] y el tamaño es 19,99 × 15,0 × 3,03 nm ³ . Los espacios de celosía a lo largo de la dirección de deslizamiento para las superficies de Au (111), Au (110) y Au (001) son 9,99 Å, 4,08 Å y 4,08 Å, respectivamente. Si no se indica, se adopta el Au (111) como sustrato. En las simulaciones, se modelan varios tamaños y formas de escamas diferentes. La forma de laminilla predeterminada es un cuadrado con un tamaño de 5,8 nm (el número de átomos N =1344). La x -El eje está a lo largo de la dirección del sillón del grafeno y el y -eje está a lo largo de la dirección en zigzag, con la z -eje normal al grafeno.

Las fuerzas interatómicas dentro de Au se derivan de un potencial del método del átomo incrustado (EAM) [32]. El potencial EAM ha tenido mucho éxito en el modelado de las propiedades elásticas, las energías de formación de defectos y los mecanismos de fractura de varios metales [32, 33]. También se ha aplicado con éxito para describir las propiedades superficiales de los metales, como las energías superficiales y las reconstrucciones superficiales [32,33,34]. El potencial AIREBO ampliamente utilizado se aplica para describir la interacción de los átomos dentro del grafeno [35]. La interacción entre el grafeno y el sustrato de Au está modelada por el potencial estándar de Lennard-Jones (LJ) que se ha empleado para estudiar muchos fenómenos de desequilibrio como la fricción y la difusión de grupos de oro en el grafito [36, 37]. Los parámetros LJ [28, 29] son: ε =22,0 meV y σ =2,74 Å. Las simulaciones MD se llevan a cabo utilizando el simulador masivamente paralelo atómico / molecular a gran escala (LAMMPS) [38]. En las simulaciones, la escama de grafeno se coloca inicialmente sobre la superficie del sustrato de Au. Una vez que el sistema de fricción está completamente relajado, el átomo virtual comienza a deslizarse a lo largo de la x negativa dirección con una velocidad constante.

Resultados y discusiones

La figura 2 muestra la fuerza de fricción en función de la distancia de deslizamiento a varias cargas normales. En este artículo, la distancia de deslizamiento es la del átomo virtual. La fuerza de fricción se mide por la deformación del resorte como en un experimento AFM. La escama de grafeno tiene una forma cuadrada con un tamaño de 5,8 nm y consta de 1344 átomos. Está claro que las fuerzas de fricción experimentan un aumento continuo seguido de caídas bruscas, que es típico del movimiento de pegado-deslizamiento. Las caídas abruptas en la fuerza de fricción conducen a la disipación de energía e implican la ocurrencia de transiciones entre múltiples estados metaestables con mínimos de energía potencial local [39]. Es razonable que la fuerza de fricción aumente con la carga L. Para explorar el efecto de tamaño, otros dos copos cuadrados con tamaños de 2.0 nm ( N =160 átomos) y 10,0 nm ( N =3936 átomos) se adoptan. La variación de la fuerza de fricción y la fuerza de fricción promedio para diferentes tamaños de escamas durante el proceso de deslizamiento se muestran en la Fig. 3. En cuanto a la escama de 5.8 nm, también se puede observar una fricción obvia de pegado-deslizamiento tanto para 2.0 como para 10. escamas nm. Además, existe claramente un efecto de tamaño en la fuerza de fricción promedio por átomo F _fric / N, consulte la Fig. 3c. Bajo la misma carga, las fuerzas de fricción promedio por átomo F _fric / N son más grandes para un copo más pequeño. Este efecto de tamaño resulta del papel progresivamente decreciente de los bordes en la fricción con el aumento del tamaño de las escamas [40, 41]. Cabe señalar que tanto los experimentos QCM como las simulaciones MD encontraron que la fricción de los grupos de adsorbato disminuye con el aumento de su tamaño [18,19,20,21,22], de acuerdo con nuestras simulaciones. Sin embargo, la dependencia del tamaño de la fricción en los experimentos de QCM y las simulaciones de MD se explica por la conmensurabilidad interfacial dependiente del tamaño [18,19,20,21,22].

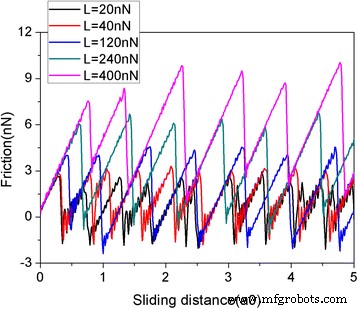
Fuerza de fricción en función de la distancia de deslizamiento a diversas cargas normales (L). La escama tiene una forma cuadrada con un tamaño de 5,8 nm. Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

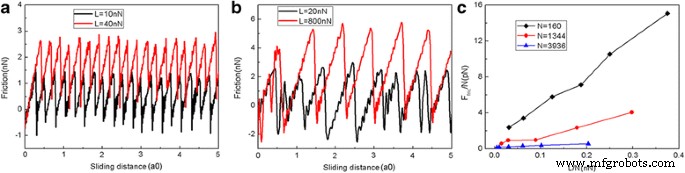
La variación de la fuerza de fricción y la fuerza de fricción promedio para diferentes tamaños de escamas. La fuerza de fricción típica en función de la distancia de deslizamiento para 2,0 nm ( N =160 átomos) escamas ( a ) y 10 nm ( N =3936 átomos) escamas ( b ). c La fuerza de fricción promedio por átomo ( F _fric / N) en función de la carga por átomo (L / N). Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

Dado que la forma del deslizador juega un papel importante en la determinación de la fricción [42, 43], para explorar más el efecto de la forma de las escamas en el proceso de fricción, también modelamos el proceso de fricción deslizante utilizando una escama de grafeno redonda ( N =1080 átomos) y una escama triangular de grafeno ( N =654 átomos). La Figura 4 muestra la variación de las fuerzas de fricción típicas y las fuerzas de fricción promedio para diferentes formas de escamas durante el proceso de deslizamiento. Como se muestra en la Fig. 4a, b, con cargas pequeñas ( L =20 nN para copos redondos y L =10 nN para escamas triangulares), la fuerza de fricción fluctúa alrededor de cero continuamente y se puede observar una fricción súper baja (superlubricidad). Sin embargo, con grandes cargas normales ( L =400 nN para hojuelas redondas y L =200 nN para escamas triangulares), las escamas exhiben un movimiento obvio de pegado-deslizamiento y una gran fuerza de fricción [39]. Bajo la misma carga, las fuerzas de fricción promedio por átomo F _fric / N son los más grandes para el copo cuadrado y los más pequeños para el copo triangular, mientras que F _fric / N para las escamas redondas están en el medio. Además, la diferencia de las fuerzas de fricción promedio por átomo F _fric / N entre la hojuela redonda y triangular es bastante pequeña. Pero F _fric / N para la hojuela cuadrada es mucho más grande. Por lo tanto, está claro que la forma de las escamas juega un papel vital en el proceso de deslizamiento.

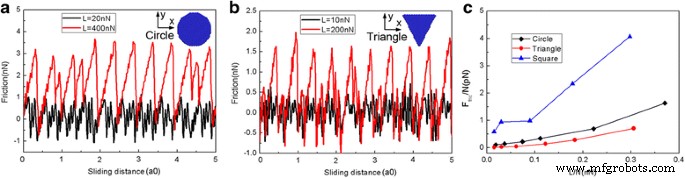
La variación de la fuerza de fricción y la fuerza de fricción promedio para diferentes formas de escamas. La fuerza de fricción típica en función de la distancia de deslizamiento de la ronda ( N =1080 átomos) escamas ( a ) y triangular ( N =654 átomos) escamas ( b ). c La fuerza de fricción promedio por átomo ( F _fric / N) en función de la carga por átomo (L / N). Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

Es bien sabido que la orientación de las escamas con respecto al sustrato también es crítica para determinar la fricción [42]. Para explorar el efecto de orientación sobre la fricción, la escama de grafeno se gira en sentido antihorario en diferentes ángulos alrededor de la z -Eje perpendicular al contacto. El ángulo de rotación de 0 ° (sin rotación) corresponde a la situación en la que x -el eje está a lo largo de la dirección del sillón del grafeno, mientras que el ángulo de rotación de 90 ° corresponde a la situación en la que x -Eje está a lo largo de la dirección en zigzag. La variación de la fuerza de fricción en función de la distancia de deslizamiento para la laca cuadrada de 5.8 nm con diferentes ángulos de rotación en L =240 nN se muestra en la Fig. 5. Las fuerzas de fricción promedio correspondientes F _fric para diferentes ángulos de rotación a diferentes cargas normales se calculan como se muestra en la Fig.6. Es obvio que para las escamas con θ =15 ° y θ =45 °, las fuerzas de fricción fluctúan alrededor de cero continuamente y se puede observar superlubricidad, ver Fig. 5b, d. Además, se puede observar una pequeña diferencia en las fuerzas de fricción promedio para escamas con θ =15 ° y θ =45 °, ver Fig. 6. Sin embargo, para las escamas con θ =30 °, 60 ° y θ =90 °, el las escamas exhiben un obvio movimiento de pegado-deslizamiento y una fuerza de fricción relativamente grande. Además, la fuerza de fricción promedio es mayor para un ángulo de rotación mayor para las escamas con θ =30 °, 60 ° y θ =90 °. Las fuerzas de fricción de las escamas con rotación son mucho menores que las de las escamas sin rotación (θ =0 °).

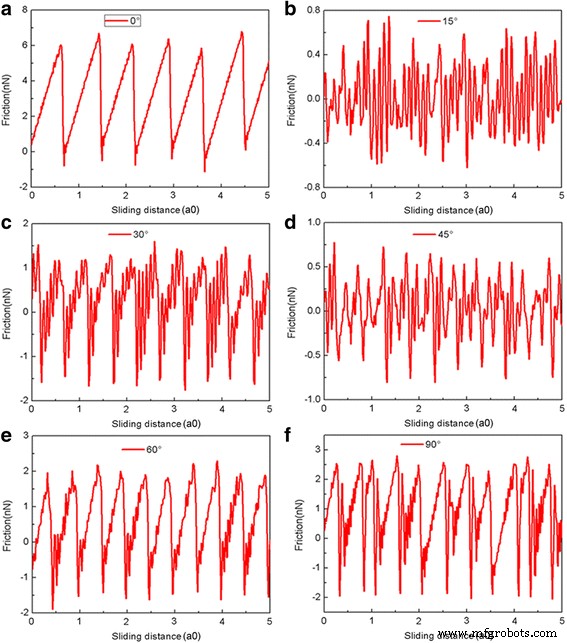
La fuerza de fricción frente a la distancia de deslizamiento de la escama cuadrada de 5.8 nm en L =240 nN para diferentes ángulos de rotación (θ =0 °, 15 °, 30 °, 45 °, 60 °, 90 °). un - f corresponden al ángulo de rotación 0 ° ~ 90 °, respectivamente. Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

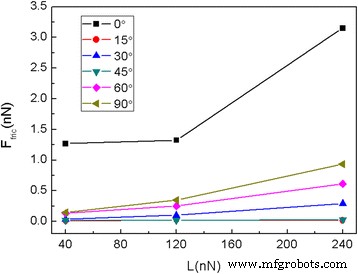
La fuerza de fricción promedio Ffric de la laminilla cuadrada de 5.8 nm para diferentes ángulos de rotación a diferentes cargas normales

El hecho de que el oro monocristalino exhiba importantes efectos anisotrópicos nos anima a estudiar más a fondo el efecto de la orientación cristalina del sustrato en el proceso de fricción. Llevamos a cabo simulaciones MD para dos combinaciones más de orientación de cristal y dirección de deslizamiento, es decir, (001) [100] y (110) [001]. La fuerza de fricción y la fuerza de fricción promedio F _fric de la escama cuadrada de 5,8 nm que se desliza sobre los sustratos de Au con diferente orientación de cristal se muestran en las Figs. 7 y 8, respectivamente. Como era de esperar, la fuerza de fricción aumenta con la carga normal. Se puede ver que bajo la misma carga, las fuerzas de fricción para las superficies de Au (001) y Au (110) son mayores que las de la superficie de Au (111), y las fuerzas de fricción para la superficie de Au (110) son las más grande.

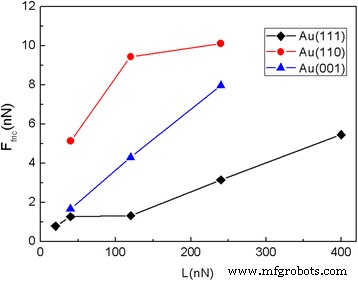
La fuerza de fricción de la laminilla cuadrada de 5,8 nm que se desliza sobre el ( a ) Au (001) y ( b ) Au (110) superficies en función de la distancia de deslizamiento a diferentes cargas normales. Aquí, a1 (=4.08 Å) es el espaciado de celosía de Au (001) a lo largo de la dirección de deslizamiento y a2 (=4.08 Å) es el espaciado de celosía de Au (110) a lo largo de la dirección de deslizamiento

La fuerza de fricción promedio F _fric de la escama cuadrada de 5.8 nm que se desliza sobre los sustratos de Au con diferente orientación de cristal a diferentes cargas normales

Según el conocido modelo de Prandtl-Tomlinson [44], la fuerza de fricción está estrechamente relacionada con la ondulación de energía interfacial [45,46,47]. Para explorar los mecanismos subyacentes detrás del efecto anisotrópico significativo de la fricción, calculamos la energía potencial de interacción entre las escamas y el sustrato de Au a medida que cambiamos la posición de las escamas [46]. La energía potencial se calcula para una lama rígida a una altura fija que corresponde a la altura media para la carga dada [29]. Tres gráficos de contorno típicos que representan la variación espacial de la energía potencial para las superficies de Au (111), Au (110) y Au (001) en L =120 nN se muestran en la Fig. 9a – c, respectivamente. Para obtener los mapas de superficie de energía potencial (PES) en la Fig. 9, usamos 21 puntos de malla a lo largo de la x y y direcciones. En la Fig. 9, las ondulaciones de energía calculadas para Au (111), Au (110) y Au (001) son 3,5 eV, 66,6 eV y 29,1 eV, respectivamente. En la Fig. 9a-c, una línea negra sólida ( y =0) en los mapas de PES se utiliza para mostrar la trayectoria de deslizamiento de la laca. La energía potencial de interacción grafeno-oro a lo largo de la trayectoria de deslizamiento de Au (111), Au (110) y Au (001) también se representa en la Fig. 9d-f, respectivamente. Las ondulaciones de energía a lo largo de la trayectoria de deslizamiento para Au (111), Au (110) y Au (001) en la Fig. 9 son 3.5 eV, 59.7 eV y 29.1 eV, respectivamente. Puede verse claramente que la amplitud de la ondulación de energía muestra el mismo efecto anisotrópico que la fricción. La ondulación de energía para las superficies de Au (001) y Au (110) es mayor que la de la superficie de Au (111), y la ondulación de energía para la superficie de Au (110) es la mayor. Por tanto, esto explica claramente el importante efecto anisotrópico de la fricción durante el proceso de deslizamiento [45,46,47]. El hallazgo de que la fuerza de fricción disminuye con la disminución de la fuerza de interacción grafeno-sustrato (corrugación de energía) es consistente con las simulaciones MD [16] y el experimento QCM [17].

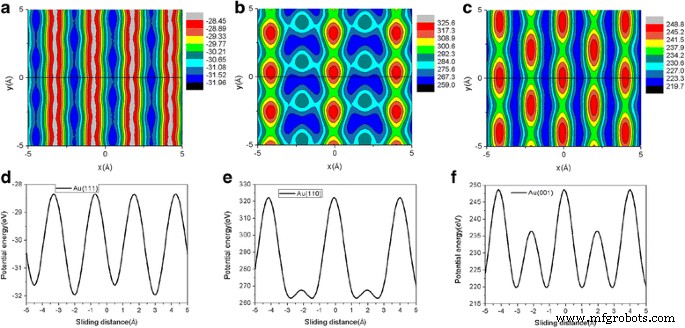
Mapas de contorno de la energía potencial para la superficie de Au (111), Au (110) y Au (001) en L =120 nN se muestran en a - c , respectivamente. Se adopta el copo de grafeno cuadrado de 5,8 nm. En a - c , una línea negra sólida ( y =0) en los mapas se utiliza para mostrar la trayectoria de deslizamiento de la laca. La energía potencial de interacción grafeno-oro a lo largo de la trayectoria de deslizamiento de la superficie de Au (111), Au (110) y Au (001) también se representa en d . - f , respectivamente. La unidad de la energía potencial es eV. La altura promedio de la escama en L =120 nN para la superficie de Au (111), Au (110) y Au (001) es 2,36 Å, 2,1 Å y 2,17 Å, respectivamente

Con el fin de igualar mejor las condiciones experimentales reales, realizamos simulaciones MD de fricción deslizante sin la restricción de movimiento del grafeno en el y dirección, en cuyo caso la laca puede girar y moverse en y dirección. La Figura 10 muestra la fuerza de fricción en función de la distancia de deslizamiento a varias cargas normales para la escama de grafeno con una forma cuadrada y un tamaño de 5,8 nm que consta de 1344 átomos. Aunque los valores de la fuerza de fricción han cambiado, se puede ver que las fuerzas de fricción experimentan un aumento continuo seguido de caídas abruptas, que es un movimiento obvio de pegado-deslizamiento similar a la figura 2. La fuerza de fricción aumenta con la carga como se esperaba. También estudiamos el proceso de fricción de otros dos copos de grafeno cuadrados con tamaños de 2,0 nm ( N =160 átomos) y 10,0 nm ( N =3936 átomos) sin la restricción de movimiento del grafeno en el y dirección. La variación de la fuerza de fricción y la fuerza de fricción promedio para diferentes tamaños de escamas durante el proceso de deslizamiento se muestran en la Fig. 11. Al igual que en la Fig. 3, también observamos una fricción obvia de pegado-deslizamiento para las escamas de 2.0 y 10 nm. Además, existe un efecto de tamaño en la fuerza de fricción promedio por átomo F _fric / N, consulte la Fig. 11c. Bajo las mismas cargas, las fuerzas de fricción promedio por átomo F _fric / N son más grandes para una escama más pequeña, que es un efecto típico de tamaño de la fricción. En general, encontramos que los principales hallazgos de las simulaciones MD del proceso de fricción con y -el movimiento de dirección de la escama restringido aún se mantiene después de relajar la restricción de movimiento de la escama de grafeno en el y dirección durante el deslizamiento.

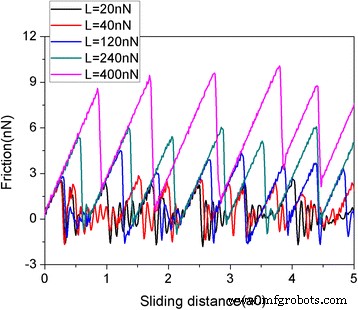
Fuerza de fricción en función de la distancia de deslizamiento a varias cargas normales ( L ) para el proceso de fricción sin la restricción de movimiento del grafeno en el y dirección. La escama tiene una forma cuadrada con un tamaño de 5,8 nm. Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

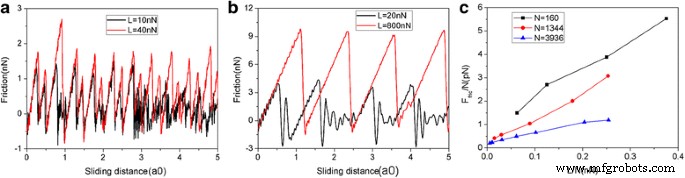
La variación de la fuerza de fricción y la fuerza de fricción promedio para diferentes tamaños de escamas para el proceso de fricción sin la restricción de movimiento del grafeno en el y dirección. La fuerza de fricción típica en función de la distancia de deslizamiento para 2,0 nm ( N =160 átomos) escamas ( a ) y 10 nm ( N =3936 átomos) escamas ( b ). c La fuerza de fricción promedio por átomo ( F _fric / N) en función de la carga por átomo (L / N). Aquí, a0 (=9,99 Å) es el espaciado de celosía de Au (111) a lo largo de la dirección de deslizamiento

Conclusiones

En este trabajo, se emplean simulaciones de dinámica molecular para investigar los comportamientos de fricción por deslizamiento de las escamas de grafeno móviles sobre un solo sustrato de oro cristalino. Se estudian a fondo los efectos del tamaño de las escamas, la forma de las escamas, el ángulo de rotación relativo y la orientación del cristal del sustrato. Se encuentra que existe un efecto de tamaño en los comportamientos de fricción. Bajo la misma carga, las fuerzas de fricción promedio por átomo F _fric / N son más grandes para una escama de grafeno más pequeña. También se encuentra que la forma de las escamas juega un papel importante en el proceso de fricción. Las fuerzas de fricción promedio por átomo F _fric / N para las escamas cuadradas son mucho más grandes que las de las escamas triangulares y redondas. Además, las fuerzas de fricción promedio por átomo F _fric / N para el copo triangular son los más pequeños. También encontramos que el efecto de la orientación de las escamas de grafeno en relación con el sustrato de Au es fundamental para determinar la fricción. Las fuerzas de fricción de las escamas de grafeno que se deslizan a lo largo de la dirección del sillón son mucho mayores que las de las escamas con rotación. Las fuerzas de fricción superbajas se pueden observar para escamas con θ =15 ° y θ =45 °. Además, la fuerza de fricción es mayor para un ángulo de rotación mayor para las escamas con θ =30 °, 60 ° y θ =90 °. Además, se encuentra que la fricción exhibe un efecto anisotrópico significativo. Las fuerzas de fricción para las superficies de Au (001) y Au (110) son mayores que las de la superficie de Au (111), y las fuerzas de fricción para la superficie de Au (110) son las mayores. Este efecto anisotrópico de la fricción se atribuye al efecto anisotrópico de la ondulación de energía potencial. Estos resultados no solo proporcionan información sobre los mecanismos subyacentes del deslizamiento de las escamas de grafeno sobre el sustrato de oro, sino que también pueden orientar el diseño y la fabricación de dispositivos basados ​​en grafeno a nanoescala.

Identificación de macromoléculas características de genotipos de Escherichia coli mediante microscopio de fuerza atómica Mapeo mecánico a nanoescala Modificación del cocatalizador de aleación de PtNi del híbrido g-C3N4 / GO sensibilizado con eosina Y para una evolución eficiente del hidrógeno fotocatalítico de luz visible