Conductividad térmica de dos tipos de alótropos de carbono 2D:un estudio de dinámica molecular

Resumen

Las propiedades térmicas de los dos nuevos alótropos de carbono 2D con anillos de cinco, cinco y ocho miembros se exploran mediante simulaciones de dinámica molecular. Nuestros resultados revelan que la conductividad térmica aumenta monótonamente al aumentar el tamaño. Las conductividades térmicas de tamaños infinitos se obtienen por relaciones lineales de la longitud inversa y la conductividad térmica inversa. La conductividad térmica convergente obtenida por extrapolación en el método de dinámica molecular de no equilibrio inverso se encuentra razonablemente de acuerdo con la del método de dinámica molecular de equilibrio. La conductividad térmica mucho más baja, en comparación con el grafeno, se atribuye a la menor velocidad del grupo de fonones y al camino libre medio de fonones. También se exploran los efectos de la temperatura y la deformación sobre la conductividad térmica. La conductividad térmica disminuye al aumentar la temperatura y también se puede ajustar mediante ingeniería de deformación en un amplio rango. El efecto de la deformación en TC se explica bien mediante el análisis de espectros de vibración de fonones. Este estudio proporciona información física sobre las propiedades térmicas de los dos alótropos de carbono en diferentes condiciones y ofrece pautas de diseño para aplicaciones de nuevos dispositivos relacionados con alótropos de carbono bidimensionales.

Introducción

Los materiales de carbono, por ejemplo, diamante [1], nanotubos de carbono [2, 3, 4, 5] y grafeno [6, 7, 8, 9, 10, 11, 12], han estimulado tremendos intereses de investigación debido a su excelente propiedades de transporte térmico. Especialmente los materiales de carbono de baja dimensión muestran propiedades sobresalientes en el transporte de calor. Como material 1D, la alta conductividad térmica (TC) de un solo nanotubo de carbono se ha observado mediante experimentos [2, 3] y estudios teóricos [4, 5]. Además, como material de carbono plano bidimensional (2D) de un solo átomo de espesor, el grafeno se considera un material revolucionario para la futura generación de compuestos reforzados termoconductores debido a su alto TC [6,7,8,9,10 , 11,12]. También se informa que el TC de graphyne puede alcanzar el 40% del grafeno y tiene aplicaciones potenciales en la gestión térmica [13,14,15].

Inspirados por las fascinantes características de estos alótropos de carbono, los investigadores han realizado intensos esfuerzos para estudiar los alótropos de carbono y sus derivados en los últimos años. Los enfoques experimentales y teóricos se han adoptado para investigar los nuevos alótropos de carbono 2D, como el sp ² -como capa de carbono con anillos de cinco, seis y siete miembros [16]; Carbono amorfo 2D con anillos de cuatro miembros [17]; pentaheptito de carbono plano [18]; Semiconductor de carbono 2D con patrones de defectos [19]; varias redes 2D de carbono plano [20]; octagrafeno [21]; T-grafeno [22]; y H-net [23]. Las identificaciones de las propiedades únicas de estos alótropos de carbono 2D son importantes para las generaciones futuras de nanomateriales en campos electrónicos, fotónicos y térmicos [16,17,18,19,20,21,22,23].

Con un creciente interés en explorar nuevas estructuras de los alótropos de carbono 2D, Su et al. [24] propuso dos nuevos alótropos de carbono 2D, energéticamente competitivos y cinéticamente estables, compuestos de octágonos y pentágonos mediante el cálculo del primer principio. La estabilidad cinética de estas dos hojas de carbono se confirmó calculando sus curvas de dispersión de fonones. Debido al hecho de que las estructuras de estos dos alótropos de carbono pueden verse como una copia de la cinta de anillos de cinco, cinco y ocho miembros (558) a lo largo de una trayectoria en línea recta y a lo largo de una trayectoria en zigzag, estos dos alótropos de carbono se denominan así octágono y pentágono grafeno-línea (OPG-L) y octágono y pentágono grafeno-zigzag (OPG-Z), respectivamente. La energía de formación de estos dos alótropos de carbono es de 0,31 eV / átomo y 0,34 eV / átomo, respectivamente. Los valores son mucho más bajos que la energía de formación del grafino sintetizado previamente, es decir, 0,76 eV / átomo [25]. Se observa que el OPG-Z posee una notable anisotropía de la estructura electrónica que tiene aplicaciones potenciales en dispositivos electrónicos [24]. En consecuencia, para cumplir con los requisitos de las aplicaciones electrónicas de OPG-L y OPG-Z, es inevitable y necesario investigar las propiedades de disipación térmica de las dos estructuras novedosas. Hasta ahora, las propiedades térmicas de estas dos estructuras aún no están claras.

En este trabajo, investigamos las propiedades térmicas de los dos nuevos alótropos de carbono 2D utilizando simulaciones de dinámica molecular. Se exploran los efectos del tamaño, la deformación y la temperatura en el TC. Los resultados se analizan calculando la densidad de vibración de estados (VDOS) de fonones. Nuestra investigación de las propiedades térmicas de estos dos alótropos de carbono indica sus posibles aplicaciones en dispositivos de gestión térmica.

Modelo y métodos

Las estructuras de OPG-L (Fig. 1a) y OPG-Z (Fig. 1b) contienen células representativas compuestas de octágonos y pentágonos [24]. Para distinguir los tipos de bordes de las estructuras, definimos la quiralidad de sillón y zigzag al igual que el grafeno (ver Fig. 1). Estas dos estructuras pueden estar formadas por la cinta representativa 558 indicada por los átomos rojos usando simetría de traslación a lo largo de las filas verdes.

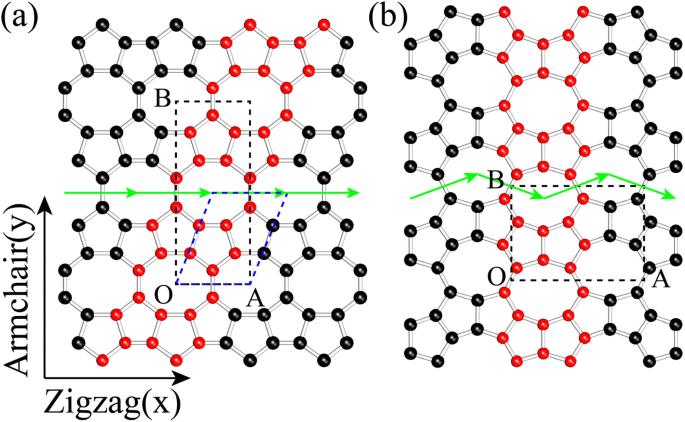
Los modelos esquemáticos de a OPG-L y b OPG-Z. Los cuadros de trazos negros son las celdas unitarias ortogonales de OPG-L y OPG-Z, donde OA y OB son vectores de celosía. La celda primitiva de OPG-L se muestra en un marco punteado azul, mientras que la celda primitiva de OPG-Z es la misma que la celda de cristal

Todas las simulaciones de MD se realizan utilizando el paquete de simulador masivamente paralelo atómico / molecular a gran escala (LAMMPS) [26]. Usamos el potencial Tersoff optimizado de Lindsay y Broido [27], con pequeñas modificaciones, es decir, potencial Tersoff optimizado modificado, para describir las interacciones entre los átomos de carbono. Lindsay y Brodio optimizaron dos parámetros en comparación con el potencial de Tersoff original [28], uno para el ángulo de enlace de equilibrio y otro para la fuerza de interacción atractiva. De acuerdo con este potencial de Tersoff optimizado [27], la longitud del enlace de equilibrio en el grafeno es 1,4388 Å, que es mayor que el valor experimental de 1,42 Å [29]. Porque los únicos parámetros relacionados con la longitud en el potencial de Tersoff son λ ₁ en la función repulsiva ( f ^R = A exp. (- λ ₁ r )) y λ ₂ en la función atractiva ( f ^A = B exp (- λ ₂ r )), podemos obtener la longitud de enlace correcta multiplicando estos dos parámetros por un factor de 1,4388 / 1,42. Es decir, cambiamos λ ₁ desde 3.4879 Å ⁻¹ a 3.5333 Å ⁻¹ y cambie λ ₂ desde 2.2119 Å ⁻¹ a 2.2407 Å ^{- 1} . Estas modificaciones solo cambian la escala de longitud del potencial de manera global. Con base en este potencial de Tersoff optimizado modificado, los parámetros de celosía de equilibrio correspondientes en la simulación de MD son los siguientes:OA =3.63 Å, OB =9.38 Å en OPG-L y OA =6.78 Å, OB =5.04 Å en OPG-Z, que son muy de acuerdo con el estudio anterior de Su et al. [24], es decir, OA =3.68 Å, OB =9.12 Å en OPG-L y OA =6.90 Å, OB =4.87 Å en OPG-Z.

Se realizan simulaciones de dinámica molecular inversa en no equilibrio (rNEMD) [30] para calcular el TC. Las condiciones de contorno periódicas se adoptan en las dimensiones xey. Las estructuras de OPG-L y OPG-Z se optimizan inicialmente mediante la versión Polak-Ribiered del algoritmo de gradiente conjugado [31], y posteriormente se emplea un baño termal Nosé-Hoover de 0,25 ns [32, 33] para garantizar que el sistema alcance el estado de equilibrio a 300 K (con un intervalo de tiempo de 0,25 fs). Después de acercarse al estado de equilibrio, el modelo se divide en 50 losas a lo largo de la dirección de transferencia de calor. Como se muestra en la Fig.2a, la 1ra losa se asigna como disipador de calor mientras que la 26a (losa del medio de la muestra) es la fuente de calor, y el flujo de calor se transfiere desde la fuente de calor (región caliente) al disipador de calor ( región fría). La dirección de transporte del flujo de calor se define como la dirección de la longitud (L) mientras que la dirección transversal es la dirección de la anchura (W). El flujo de calor J se libera / inyecta entre estas dos losas intercambiando las energías cinéticas entre el átomo más caliente, que tiene la energía cinética más alta, en la losa del disipador de calor y el átomo más frío, que tiene la energía cinética más baja, en la fuente de calor. losa. El flujo de calor J se puede obtener calculando la cantidad de intercambio de energía cinética entre el disipador de calor y la losa de la fuente de calor de acuerdo con las siguientes ecuaciones.

$$ J \ kern0.5em =\ kern0.5em \ frac {\ sum _ {\ mathrm {Nswap}} \ frac {1} {2} \ left ({mv} _h ^ 2- {mv} _c ^ 2 \ right )} {t _ {\ mathrm {swap}}}, $$ (1)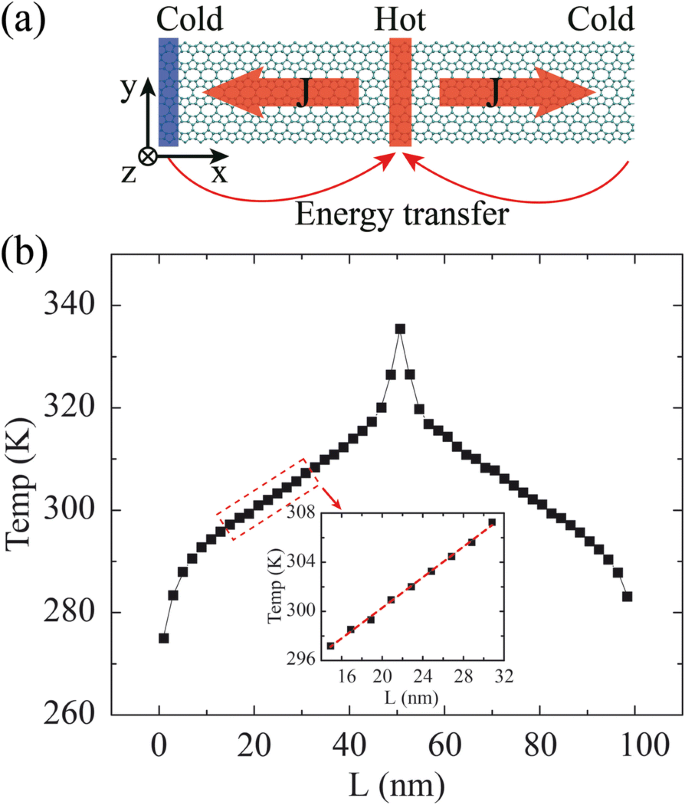

un Gráfico esquemático del método rNEMD. El flujo de calor se transfiere desde la fuente de calor (región caliente) al disipador de calor (región fría). La dirección de transporte del flujo de calor se define como la dirección de la longitud (L) mientras que la dirección transversal es la dirección de la anchura (W). b La distribución de la temperatura media en función de las losas

donde t _intercambiar es el tiempo total de intercambio de energía cinética, N _intercambiar denota la cantidad de pares de átomos en intercambio, m es la masa del átomo y v _h y v _c representan la velocidad de intercambio de átomos (el átomo más caliente con la energía cinética más alta en la losa del disipador de calor y el átomo más frío con la energía cinética más baja en la losa de la fuente de calor), respectivamente. La temperatura de cada placa se recopila y se promedia sobre 3,0 ns para obtener la distribución de temperatura cuando el sistema alcanza el estado estable de no equilibrio (después de 1,5 ns). El valor de TC ( κ ) se calcula utilizando la ley de Fourier como

$$ \ kappa =\ frac {J} {2A \ T parcial / \ L parcial}, $$ (2)

donde A es el área de la sección transversal de transferencia de calor ( A se obtiene multiplicando el ancho y el grosor del modelo), y ∂T / ∂L denota el gradiente de temperatura después de que el sistema alcanza el estado estable de no equilibrio (ver Fig. 2b). El factor 2 representa el hecho de que el flujo de calor se transporta en dos direcciones alejándose de la fuente de calor. Se supone que el grosor del modelo es el espacio de equilibrio entre capas del grafeno (0,34 nm) [8, 10, 34, 35].

Resultados y discusiones

Primero examinamos el efecto del tamaño del sistema en el TC de los dos alótropos de carbono. Las muestras de simulación se generan con el mismo ancho de 3 nm pero diferente longitud que varía de 50 a 1000 nm. Cabe señalar que todos los valores de la longitud de la muestra mencionados en este trabajo son la longitud efectiva ( L _ef ) de transferencia de calor. Es decir, la longitud efectiva de la muestra es la mitad de la longitud de la muestra ( L ), es decir, L _ef = L / 2, que se atribuye al flujo de calor que se transfiere desde el medio (la fuente de calor) a ambos extremos (el disipador de calor) de la muestra en el método rNEMD. En particular, hemos confirmado que el TC no depende del ancho de la muestra calculando las conductividades térmicas de muestras con una longitud fija de 50 nm pero con un ancho diferente de 3 nm, 6 nm, 9 nm y 12 nm, respectivamente, como se muestra en Fig. 3. El TC de OPG-L a lo largo del zigzag y las direcciones del sillón se denominan κ _OPG-LZ y κ _OPG-LA , respectivamente. Del mismo modo, κ _OPG-ZZ y κ _OPG-ZA se utilizan para representar el TC de OPG-Z a lo largo del zigzag y las direcciones del sillón. Los resultados de la simulación muestran que el TC de OPG-L y OPG-Z en las dos direcciones quirales aumenta monótonamente con una longitud de muestra que varía de 50 a 1000 nm. Se atribuye a que en la muestra larga, los fonones acústicos con mayor longitud de onda están implicados en la transferencia de calor [9, 36]. Respectivamente, el TC de OPG-L y OPG-Z de 50 nm y 1000 nm de longitud a lo largo de la dirección en zigzag son κ _OPG-LZ50 =125 W / mK, κ _OPG-LZ1000 =296 W / mK, κ _OPG-ZZ50 =94 W / mK y κ _OPG-ZZ1000 =236 W / mK. A lo largo de la dirección del sillón, el TC de OPG-L y OPG-Z son κ _OPG-LA50 =105 W / mK, κ _OPG-LA1000 =316 W / mK, κ _OPG-ZA50 =93 W / mK y κ _OPG-ZA1000 =214 W / mK.

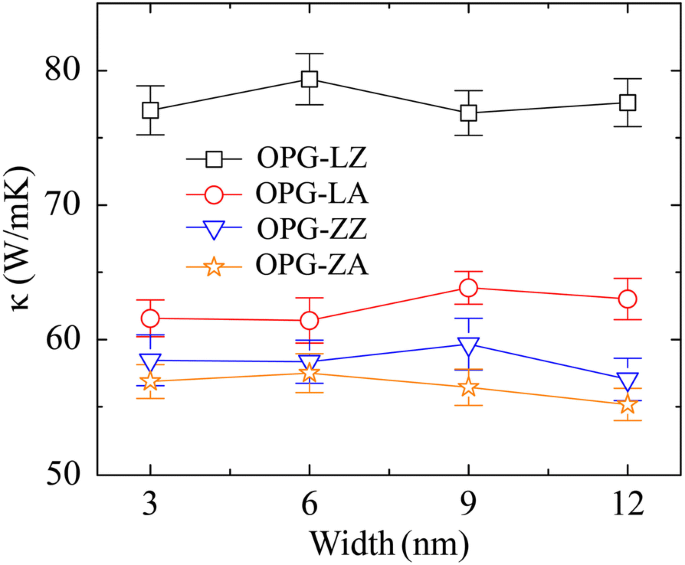
TC de OPG-L y OPG-Z en función del ancho

Para extraer el TC de muestras infinitamente largas, se emplea un procedimiento de ajuste inverso. La relación entre la longitud inversa y el TC inverso se expresa como [37,38,39]:

$$ {\ kappa} ^ {- 1} =\ kappa {} _ {\ infty} {} ^ {- 1} \ left (\ frac {2l} {L_ {eff}} + 1 \ right), $$ (3)

donde κ _∞ es el TC extrapolado de una muestra infinita, l es el phonon mean free path, y L _ef es la duración efectiva de la transferencia de calor. La ecuación (3) sugiere que la relación entre la longitud inversa y el TC inverso debería ser lineal. Como se muestra en la Fig. 4, se observa una relación lineal entre la longitud inversa y el TC inverso. Extrapolando a L ⁻¹ =0, el TC de muestras infinitas, es decir, κ _OPG-LZ =310 W / mK, κ _OPG-LA =332 W / mK, κ _OPG-ZZ =247 W / mK y κ _OPG-ZA =228 W / mK, se obtienen.

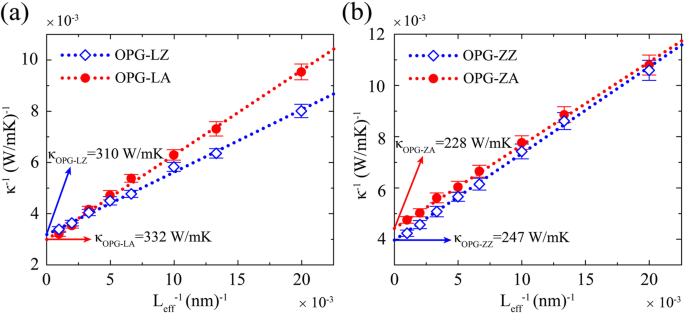
TC inverso de a OPG-L y b OPG-Z en función de la longitud inversa de la muestra a 300 K. El diamante azul abierto y los puntos rojos representan TC a lo largo del zigzag y las direcciones del sillón, respectivamente

Además, también expresamos el TC en ejecución en el método de dinámica molecular de equilibrio (EMD) estableciendo la muestra con la misma longitud y ancho de 20 nm (este tamaño de muestra de simulación ha sido probado para ser lo suficientemente grande como para eliminar efectos de tamaño finito) . Según el trabajo de Fan et al. [39, 40], los cálculos de TC en el método EMD se basan en la fórmula Green-Kubo [41, 42], en la que la TC en ejecución a lo largo de la dirección x se puede expresar de la siguiente manera:

$$ {\ kappa} _ {xx} (t) =\ frac {1} {\ kappa_B {T} ^ 2V} {\ int} _0 ^ t \ left \ langle {J} _x (0) {J} _x \ left ({t} ^ {\ hbox {'}} \ right) \ right \ rangle {dt} ^ {\ hbox {'}}, $$ (4)

donde κ _B es la constante de Boltzmann, V es el volumen del sistema, T es la temperatura absoluta del sistema, 〈 J _x (0) J _x ( t ^' )〉 Es la función de autocorrelación del flujo de calor, t es el tiempo de correlación y J _x es el flujo de calor en la dirección x. El símbolo 〈〉 representa el tiempo promedio en las simulaciones de EMD. El tiempo máximo de correlación es 2 ns, que se ha probado que es lo suficientemente grande. Como se muestra en la Fig. 5, el TC en ejecución para OPG-L y OPG-Z en dos direcciones quirales a 300 K se expresan promediando los resultados de 100 simulaciones independientes con diferente velocidad inicial. Además, podemos obtener el TC de una muestra infinita promediando el TC en ejecución en el tiempo de correlación de 1.0 a 2.0 ns. Es decir, el TC convergente de OPG-LZ, OPG-LA, OPG-ZZ y OPG-ZA son 313 W / mK, 344 W / mK, 261 W / mK y 233 W / mK, respectivamente, que están en acuerdo razonable con los resultados por extrapolación en el método rNEMD.

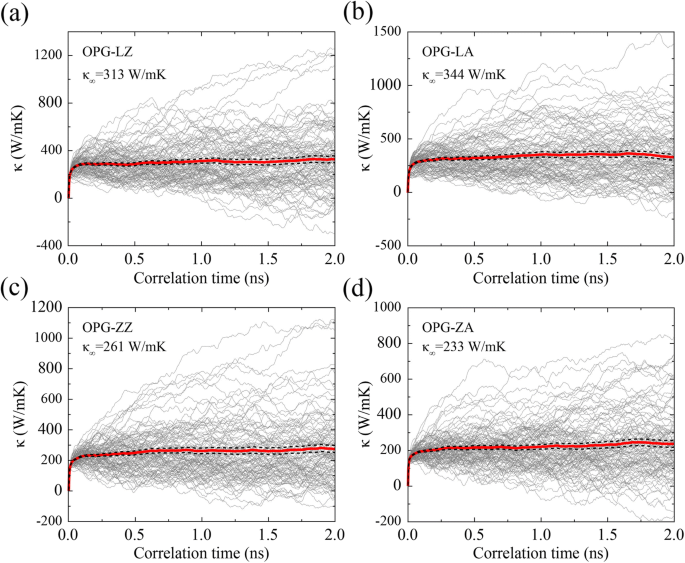
Evolución del CT de a OPG-LZ, b OPG-LA, c OPG-ZZ y d OPG-ZA a 300 K en función del tiempo de correlación. Las líneas finas representan los resultados de 100 simulaciones independientes y las líneas sólidas y discontinuas gruesas representan sus límites promedio y de error. κ _∞ es el TC de una muestra infinita, que se obtiene promediando el TC en ejecución en el tiempo de correlación de 1.0 a 2.0 ns

Se encuentra que el CT de estos dos alótropos de carbono es mucho más bajo que el del grafeno (3000-5000 W / mK) [7, 43] . Para explicar este fenómeno y explorar la percepción física, calculamos tres parámetros importantes, es decir, C _v , v _g y l , basado en la ecuación clásica de transporte térmico de celosía:

$$ \ kappa =\ frac {1} {3} {C} _v {v} _gl, $$ (5)

donde C _v es la capacidad calorífica, v _g es la velocidad efectiva del grupo de fonones y l es el camino libre medio de fonones.

La muestra con una longitud y un ancho de 20 nm se adopta para investigar la capacidad calorífica a 300 K. La capacidad calorífica se calcula siguiendo el enfoque de McGaughey y Kaviany [44], que se ha utilizado en el enfoque de la dinámica molecular del equilibrio. simulaciones [45]. Calculamos la energía total E a una temperatura de T =290 K, 295 K, 300 K, 305 K, 310 K en el conjunto canónico, y los resultados se promedian sobre 60 ps de diez simulaciones independientes con diferente velocidad inicial. Como se muestra en la Fig. 6, la pendiente en el ajuste lineal de la curva de energía-temperatura es la capacidad calorífica.

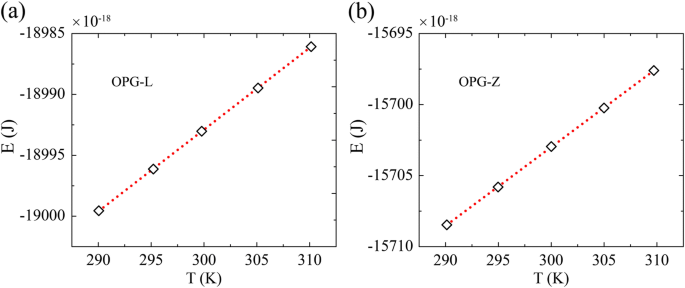
La variación de energía en función de la temperatura para a OPG-L y b OPG-Z. La pendiente de la curva de energía-temperatura denota la capacidad calorífica. Las capacidades caloríficas correspondientes son 4.163 E-23 J / K y 4.126 E-23 J / K, respectivamente, por átomo

Cabe señalar que la velocidad del grupo de fonones que calculamos aquí es la velocidad efectiva del grupo de fonones v _g en lugar de la velocidad promedio del grupo de fonones v . Como se muestra en la Fig. 7, la velocidad efectiva del grupo de fonones se puede obtener comparando los resultados de las simulaciones de rNEMD y EMD. Es decir, una longitud efectiva del sistema L _ef se puede definir en el método EMD multiplicando el límite superior del tiempo de correlación t en la fórmula Green-Kubo Eq. (4) por una velocidad de grupo de fonones efectiva v _g , L _ef ≈ v _g t . El TC κ en ejecución ( t ) del método EMD también se puede considerar en función de la longitud del sistema κ ( L _ef ). En comparación con la velocidad promedio del grupo de fonones, la velocidad efectiva del grupo de fonones es una estimación aproximada, pero se ha utilizado ampliamente en el estudio del transporte térmico en modelos de celosía de baja dimensión [46] y también se ha utilizado para grafeno [40] y alótropos de Si [39].

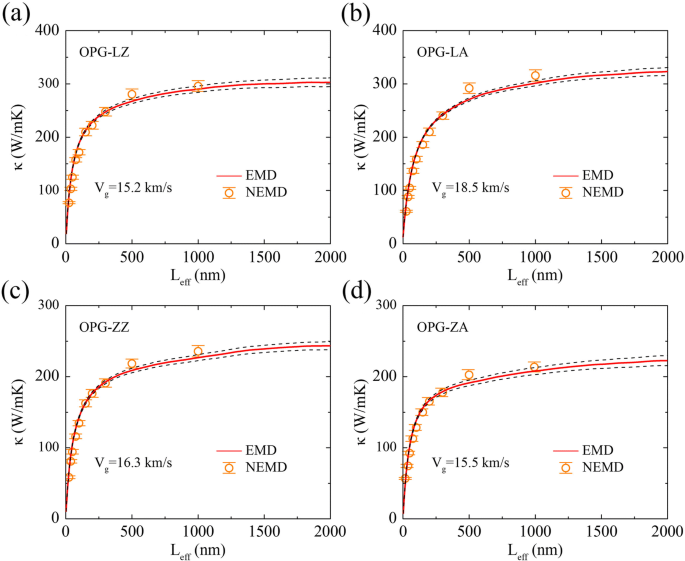
TC de a OPG-LZ, b OPG-LA, c OPG-ZZ y ( d ) OPG-ZA en función de la longitud de muestra efectiva de simulaciones EMD y rNEMD. La velocidad efectiva del grupo de fonones V _g se obtiene combinando simulaciones EMD y rNEMD

Basado en Eq. (3), el camino libre medio de fonones se puede obtener mediante extrapolación en el método rNEMD. Para comparar el TC de estos dos alótropos de carbono con el del grafeno, también presentamos estos tres parámetros del grafeno. La capacidad calorífica del grafeno se calcula mediante el método anterior, mientras que la velocidad efectiva del grupo de fonones y la trayectoria libre media de fonones se obtienen en otros trabajos [7, 40]. Se puede encontrar que las capacidades caloríficas de estos dos alótropos de carbono son cercanas a las del grafeno; sin embargo, la velocidad efectiva del grupo de fonones y el camino libre medio de fonones son mucho más bajos que los del grafeno, lo que conduce a un TC más bajo de los dos materiales (ver Tabla 1).

Además, exploramos la dependencia de TC de la temperatura, como se muestra en la Fig. 8. La región de temperatura de 200 K a 300 K es el rango principal en el que nos enfocamos. Las muestras de simulación se generan con el mismo ancho de 3 nm pero diferente longitud de 50 nm, 75 nm, 100 nm, 150 nm y 200 nm, respectivamente. Como se muestra en la Fig. 8a, b, damos el TC inverso de OPG-LZ y OPG-LA a varias temperaturas como una función de la longitud de la muestra inversa. Similar al efecto de extrapolación en tamaño a 300 K, las conductividades térmicas de una muestra infinita a varias temperaturas se extraen mediante un procedimiento de extrapolación. Como se muestra en la Fig. 8c, d, todas las conductividades térmicas convergentes están normalizadas por el TC a 300 K ( κ ₀ ).

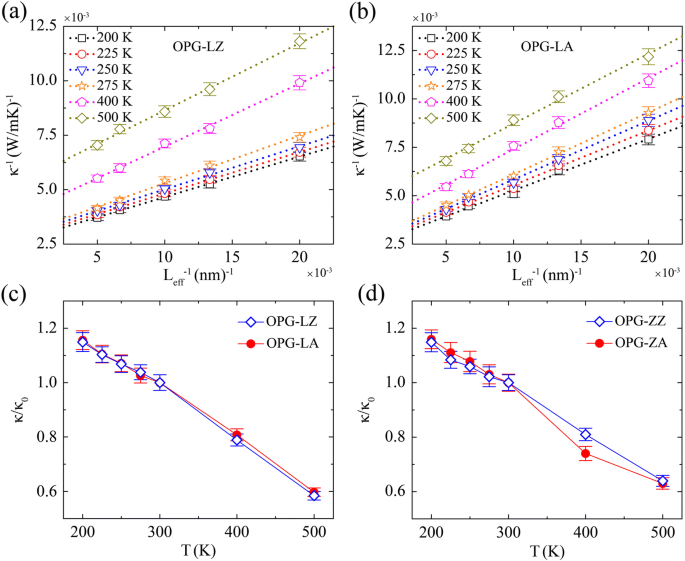
TC inverso de a OPG-LZ, b OPG-LA a varias temperaturas en función de la longitud inversa de la muestra y el TC relativo ( κ / κ ₀ ) de c OPG-L y d OPG-Z en función de la temperatura. κ ₀ es el TC a 300 K, que es 310 W / mK, 332 W / mK, 247 W / mK y 227 W / mK para κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ y κ _OPG-ZA , respectivamente

La Figura 8 indica que a lo largo de las direcciones en zigzag y del sillón, el TC disminuye al aumentar la temperatura tanto para OPG-L como para OPG-Z. La tendencia de TC varía con la temperatura (de 200 a 500 K) concuerda bien con las de estudios previos de TC del grafeno [8, 36, 47]. Este fenómeno se deriva de la mejora de los procesos de dispersión de Umklapp que desempeñan un papel fundamental en el transporte de calor [8, 36, 47]. Además, cuando la temperatura varía de 300 a 500 K, el κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ y κ _OPG-ZA cae en un 42%, 40%, 36% y 37%, respectivamente. La dependencia de TC de estos dos alótropos de carbono de la temperatura muestra que es necesario considerar los efectos de la temperatura para sus aplicaciones prácticas.

Las propiedades térmicas de los materiales bidimensionales, por ejemplo, grafeno [48, 49], siliceno [34, 50, 51] y fosforeno [37], son sensibles a la ingeniería de deformaciones. Se ha informado que el CT del grafeno con un tamaño pequeño disminuye con el aumento de la deformación por tracción [48], y el CT también puede mejorarse aumentando la deformación cuando la muestra es mayor de 500 μm [49]. Las inusuales dependencias de TC en el tamaño de la muestra y la tensión se atribuyen a la competencia entre la dispersión de límites y la dispersión de fonón-fonón. Además, se encuentra que el TC del siliceno aumenta con una pequeña deformación por tracción, pero disminuye con una gran deformación debido a la competencia entre el ablandamiento del fonón en los modos en el plano y la rigidez del fonón en los modos fuera del plano [34, 50, 51]. Por lo tanto, es importante y necesario investigar las relaciones entre el comportamiento del TC y la deformación por tracción para las estructuras OPG-L y OPG-Z.

Primero investigamos las propiedades mecánicas de estos dos alótropos de carbono. El tamaño de la muestra es de aproximadamente 5 nm de largo y 5 nm de ancho. Para evitar altas fuerzas de unión falsas y endurecimiento por deformación no física [52, 53], la distancia de corte se fija en ( R = S =1,95 Å). Esta distancia de corte en el potencial de Tersoff optimizado modificado también es coherente con la de los potenciales de Tersoff anteriores (1.8–2.1 Å) [28, 53,54,55] que se utilizan para simular el enlace C-C. Todas las simulaciones se inician relajando la configuración atomística de la estructura a un estado de energía potencial mínimo. La deformación por tracción uniaxial se aplica con una tasa de deformación de 0,0002 ps ⁻¹ . Cabe señalar que el espacio de equilibrio entre capas del grafeno (3,4 Å) se utiliza para representar la distancia de equilibrio entre capas de las dos estructuras. Las propiedades mecánicas de estos dos alótropos de carbono se enumeran en la Tabla 2, con la comparación del grafino y el grafeno [56]. Las características del superíndice de z y a representan hojas en zigzag y sillón, respectivamente.

Se ve en la Tabla 2 que a lo largo de la dirección en zigzag, los módulos de Young de OPG-L y OPG-Z son 538 GPa y 492 GPa, y a lo largo de la dirección del sillón, los módulos de Young son 648 GPa y 550 GPa, respectivamente. Indica que el módulo de Young de OPG-L y OPG-Z es cercano al de graphyne (503.1 ^z y 525.0 ^a ) pero más bajo que el del grafeno (856,4 ^z y 964.0 ^a ). Las relaciones tensión-deformación de los dos alótropos de carbono a lo largo del zigzag y las direcciones del sillón se muestran en la Fig. 9. De acuerdo con los comportamientos de fractura de estos dos alótropos de carbono, obtenemos además la deformación máxima (tensión) de estos dos alótropos de carbono. Respectivamente, a lo largo de la dirección en zigzag, la deformación máxima (tensión) del OPG-L y la OPG-Z son 17.2% y 10.9%, y a lo largo de la dirección del sillón, la deformación máxima (tensión) es 8.7% y 7.9%. Descubrimos que la estructura de OPG-L tiene una mayor resistencia bajo tensión de tracción en la dirección de zigzag. Sin embargo, en comparación con el grafino y el grafeno, las tensiones finales de los dos alótropos de carbono son menores.

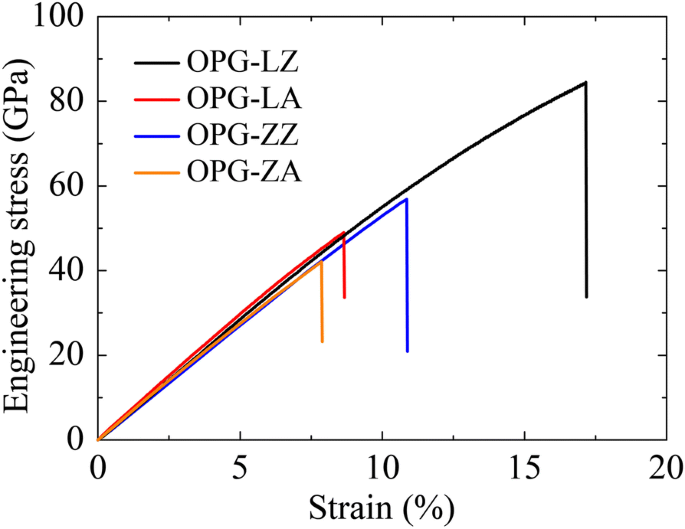
Relaciones tensión-deformación de los dos alótropos de carbono a lo largo del zigzag y las direcciones del sillón

Luego estudiamos el efecto de deformación en TC de estos dos alótropos de carbono mediante la aplicación de deformación por tracción uniaxial a lo largo de la dirección de transferencia de calor. Las muestras de simulación tienen el mismo ancho de 3 nm pero diferente longitud de 50 nm, 75 nm, 100 nm, 150 nm y 200 nm, respectivamente. Las conductividades térmicas de una muestra infinita a varias deformaciones se extraen mediante un procedimiento de extrapolación (ver Fig. 10a, b). Como se ilustra en la Fig. 10c, d, todas las conductividades térmicas convergentes están normalizadas por el TC de tensión libre a 300 K ( κ ₀ ), además damos el TC relativo ( κ / κ ₀ ) de los dos alótropos de carbono en función de varias cepas uniaxiales. La Figura 10 muestra claramente que el TC de OPG-L y OPG-Z disminuye monótonamente con el aumento de la tensión de tracción, lo cual es consistente con estudios previos en grafeno [34, 48] pero en marcado contraste con el silicene [34, 50, 51] y fosforeno [37]. Como se muestra en la Fig.10, la reducción máxima de κ _OPG-LZ , κ _OPG-LA y κ _OPG-ZZ , κ _OPG-ZA son 49%, 44%, 37% y 31%, respectivamente. En particular, el TC de OPG-L a lo largo de la dirección del zigzag se puede sintonizar a través de la tensión en un amplio rango.

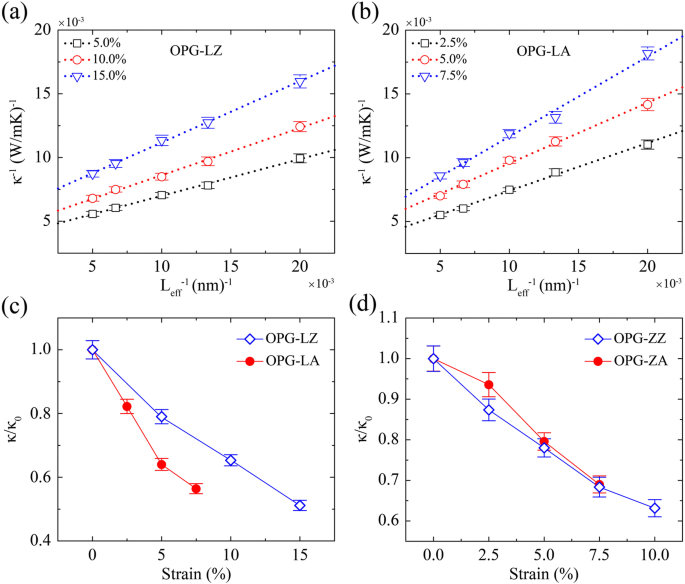
TC inverso de a OPG-LZ, b OPG-LA en varias cepas uniaxiales en función de la longitud de la muestra inversa y el TC relativo ( κ / κ ₀ ) de c OPG-L y d OPG-Z en función de la deformación. κ ₀ es el TC libre de estrés a 300 K, que es 310 W / mK, 332 W / mK, 247 W / mK y 227 W / mK para κ _OPG-LZ , κ _OPG-LA , κ _OPG-ZZ y κ _OPG-ZA , respectivamente

Con el fin de dilucidar aún más el efecto de deformación sobre las propiedades de transporte térmico de OPG-L y OPG-Z, calculamos el VDOS de fonones de OPG-LZ en la deformación típica. Los VDOS se calculan mediante una transformada de Fourier de la función de autocorrelación de la velocidad atómica. La función se define de la siguiente manera:

$$ P \ left (\ omega \ right) =\ frac {1} {\ sqrt {2 \ pi}} \ underset {0} {\ overset {\ infty} {\ int}} {e} ^ {i \ omega t} \ left \ langle \ sum \ limits_ {j =1} ^ N {v} _j (t) {v} _j (0) \ right \ rangle dt, $$ (6)

Como se ilustra en la Fig. 11, se observa el ablandamiento del fonón (desplazamiento al rojo) en direcciones dentro y fuera del plano. Este fenómeno está de acuerdo con estudios previos en grafeno bajo tensión de tracción [34, 48]. En particular, en comparación con el VDOS en dirección fuera del plano, el ablandamiento del fonón en la dirección en el plano es obvio. Indica que la disminución de TC de OPG-L y OPG-Z se debe principalmente al ablandamiento del fonón inducido por la tensión en la dirección del plano.

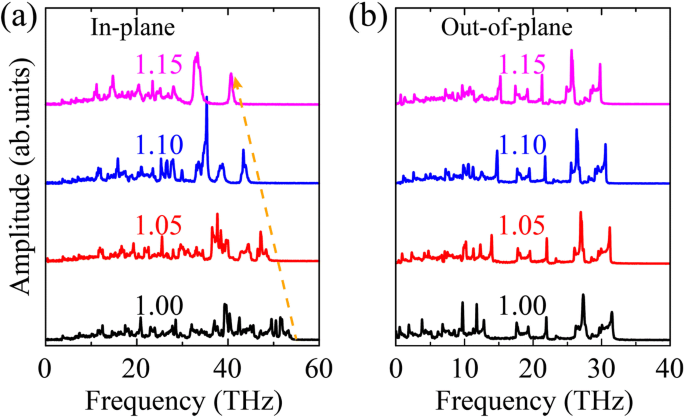
En el avión a y fuera del plano b VDOS de OPG-L versus deformación por tracción uniaxial a lo largo de la dirección de zigzag

Conclusiones

En resumen, se han realizado simulaciones de EMD y rNEMD para investigar las propiedades térmicas de los dos nuevos alótropos de carbono 2D compuestos por octágonos y pentágonos. Se obtienen los efectos de tamaño, temperatura y deformación sobre TC. Nuestros resultados revelan que el TC aumenta monótonamente con el aumento de tamaño. Las conductividades térmicas de tamaños infinitos se obtienen mediante relaciones lineales de longitud inversa y TC inversa. La TC convergente obtenida por extrapolación en el método de dinámica molecular de no equilibrio inverso se encuentra razonablemente de acuerdo con la del método de dinámica molecular de equilibrio. El TC mucho más bajo, en comparación con el grafeno, se atribuye a la menor velocidad del grupo de fonones y al camino libre medio de fonones. Nuestros hallazgos brindan información importante sobre los efectos del tamaño, la temperatura y la tensión en las propiedades de transporte térmico de OPG-L y OPG-Z, e indican aplicaciones potenciales en dispositivos de gestión térmica en campos de micro / nanoelectrónica.

Abreviaturas

558:: Anillos de cinco, cinco, ocho miembros
OPG-L:: Octagon and pentagon graphene-line
OPG-Z:: Octagon and pentagon graphene-zigzag
rNEMD:: Reverse non-equilibrium molecular dynamics
TC:: Thermal conductivity
VDOS:: Vibrational density of states

Diodo Schottky β-Ga2O3 de alto voltaje con terminación de borde implantado con argón Síntesis de NiCo2O4 similar al erizo de mar mediante una estrategia de autoensamblaje impulsada por carga para baterías de iones de litio de alto rendimiento

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias