Estrategia de superenfoque de campo cuasi lejano dependiente de la polarización de las lentes plasmónicas basadas en nanorrestación

Antecedentes

Junto con el desarrollo de imágenes de superresolución [1], la aceleración de partículas [2], el procesamiento de información óptica cuántica [3] y el almacenamiento de datos ópticos dependientes de la polarización [4], los dispositivos plasmónicos de superficie se aplican ampliamente en estas regiones mediante la modulación de la resonancia de plasmón en una magnitud de sublongitud de onda. La lente plasmónica (PL), como un dispositivo típico, posee la capacidad de imagen perfecta que fue propuesta por primera vez por J. B. Pendry en 2000 [5], y la imagen óptica de límite de sub-difracción fue demostrada experimentalmente por X. Zhang et al. 5 años después [6]. Sin embargo, el plano de imagen se limitó al campo extremadamente cercano a medida que las ondas evanescentes disminuyen exponencialmente, lo que indica un campo óptico divergente. Esta limitación lo hace impracticable para microscopios ópticos estándar [7].

En los últimos años, se han investigado varios PL basados ​​en nanoestructuras [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Estos PL no solo pueden realizar el enfoque plasmónico en el plano [8] o en el campo cercano [9], sino que también pueden poseer la capacidad de enfoque en el campo lejano [10, 11, 12, 13] que generalmente se obtienen mediante la exploración óptica. microscopio [14]. Sin embargo, estos PL mostraron una gran dificultad para realizar el enfoque más allá del límite de difracción, hasta que se empleó la relación de dispersión de la guía de ondas metal-aislante-metal (MIM) para los PL basados ​​en nano-iluminación para modular la fase en la escala de sublongitud de onda [11 , 15, 16, 17]. La modulación de fase precisa contribuye a la línea focal del límite de sub-difracción, y la luz polarizada linealmente se aplica generalmente como luz incidente para estas lentes. Pero, simplemente extendiendo el método de diseño similar de lentes nanoslit unidimensionales en dos dimensiones, el enfoque de forma circular no se puede realizar cuando el PL rotacionalmente simétrico fue iluminado por la luz polarizada linealmente [18, 19], lo que indica la fuerte dependencia de la polarización del rendimiento de enfoque. Además, la distancia focal se desvió seriamente del cálculo numérico de acuerdo con la teoría de reconstrucción del frente de onda, especialmente para los PL basados ​​en nanorretenimiento [18].

Las PL basadas en nanorrección con simetría rotacional, que se denominan lentes plasmónicas basadas en nanorrección (NRPL) para simplificar en la siguiente discusión, se reconocen como la sustitución de las lentes refractivas conversivas en los sistemas de enfoque de sublongitud de onda. Pero desde la perspectiva de la excitación de los polaritones de plasmón de superficie (SPP), la luz polarizada linealmente no es adecuada para los NRPL ya que la eficiencia de excitación es proporcional al componente del campo eléctrico radial de la luz incidente. Comparativamente, la luz radialmente polarizada con simetría cilíndrica en polarización se adapta a la propiedad estructural de los NRPL [25]. Además, utilizando un tope de apertura en forma de rosquilla [26, 27] o una placa de zona de Fresnel [28], esta luz polarizada se ha aplicado para realizar el enfoque de forma circular de sublongitud de onda. Por lo tanto, la luz polarizada radialmente se aplicó generalmente como la luz incidente de los NRPL [20, 21, 22, 23]. En comparación con el enfoque de sublongitud de onda con el filtro espacial, estos PL poseen la capacidad de modular la fase de la luz incidente en la guía de onda de sublongitud de onda. La excitación de ondas plasmónicas superficiales (SP) puede mejorar la transmisión de ondas electromagnéticas. Sin embargo, no se ha demostrado la capacidad de superenfoque de la lente plasmónica en el campo lejano. Además, aunque se ha propuesto que el NRPL compuesto modula la distancia focal [24], la distancia focal no pudo controlarse eficazmente y la energía del campo eléctrico todavía se concentra en el centro de la superficie del extremo de la lente.

En este artículo, presentamos el diseño teórico y el estudio numérico de un NRPL, con énfasis en la realización del superenfoque utilizando la propiedad de polarización de la luz incidente. Describimos el diseño teórico de los NRPL en nuestra investigación y proporcionamos el rendimiento de enfoque en la región de salida con base en la simulación numérica de dominio de tiempo de diferencia finita (FDTD). Para investigar la dependencia de la polarización del rendimiento de enfoque, las luces polarizadas lineal, circular, azimutal y radialmente se consideran todas para la iluminación. Discutimos las características de distribución del campo eléctrico en la región de salida, incluido el enfoque del límite de sub-difracción, las formas de los focos y la modulación de la distancia focal, y señalamos la importancia de la condición coaxial en el rendimiento de superenfoque.

Métodos

Los NRPL investigados en este trabajo se diseñaron utilizando la teoría de la reconstrucción del frente de onda que se aplicó ampliamente a los PL basados ​​en nanoslit [11, 15]. Para lograr el enfoque en la posición deseada, el retardo de fase relativo causado cuando la luz pasa a través del i -th nanoring individual necesita satisfacer la siguiente condición basada en la óptica geométrica:

$$ - \ varDelta \ phi \ left ({r} _i \ right) =\ frac {2 \ pi \ sqrt {f_0 ^ 2 + {r} _i ^ 2}} {\ lambda_0} - \ frac {2 \ pi \ sqrt {f_0 ^ 2 + {r} _1 ^ 2}} {\ lambda_0} +2 n \ pi $$ (1)

donde −Δ ϕ ( r _i ) es la diferencia de fase relativa entre el primer nanoring en el centro interior y el i -th nanoring, r es el radio, λ ₀ es la longitud de onda en el espacio libre de la luz incidente, n es un número entero arbitrario y f ₀ es la distancia focal diseñada.

El elemento básico de los NRPL encuestados son los nanorings modelados en la película metálica. Según Ref. [29], cuando el diámetro es mayor que la longitud de onda de la luz incidente, el nanorrenado de aire rodeado por paredes metálicas se puede aproximar al modelo de guía de ondas MIM como se ilustra en el recuadro de la Fig. 1. El retardo de fase se define principalmente por la parte real de la constante de propagación β , expresado como Re ( β ) • t , donde t es el grosor del nanoring. Según la relación de dispersión, la constante de propagación compleja β se puede calcular como:

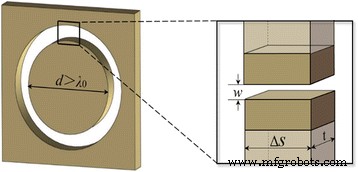
El modelo de guía de ondas MIM de una nanorrección individual incrustada en la película de oro. El recuadro da una vista ampliada de una pequeña porción arbitraria del nanoring

$$ \ tanh \ left (\ frac {w \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _d}} {2} \ right) =- \ frac {\ varepsilon_d \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _m}} {\ varepsilon_m \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _d}} $$ (2)

donde k ₀ representa el vector de onda en el vacío y ε _d y ε _m son la permitividad del dieléctrico y del metal, respectivamente. Basado en la ecuación. (2), podemos ver que la constante de propagación β depende del ancho de un nanoring. Por lo tanto, para la lente plana con un grosor dado t , el retraso de fase causado se determina simplemente por el ancho w del nanoring individual cuando la luz pasa a través de él. En nuestra investigación, el dieléctrico está configurado para ser aire con la permitividad ε _d =1, y la película de oro con un espesor t de 400 nm, cuya permitividad a la longitud de onda incidente de 650 nm es ε _m =−12,8915 + 1,2044i [15]. Además, como informamos anteriormente [16], el efecto de acoplamiento de las luces de propagación en las dos guías de ondas MIM adyacentes también juega un papel importante en el retardo de fase, especialmente cuando la pared metálica espaciada es menor que el doble de la profundidad de la piel δ _m , que puede estimarse por [30]:

$$ {\ delta} _m =\ frac {1} {k_0} {\ left | \ frac {\ mathrm {Re} \ left ({\ varepsilon} _m \ right) + {\ varepsilon} _d} {\ mathrm { Re} {\ left ({\ varepsilon} _m \ right)} ^ 2} \ right |} ^ {\ frac {1} {2}} $$ (3)

En consecuencia, la profundidad de piel calculada δ _m es de aproximadamente 28 nm. Al considerar el efecto de acoplamiento, un PL basado en nanolit con la capacidad de superenfoque de 0,38 λ ₀ en resolución se informó en nuestra investigación anterior [16]. Aquí, para analizar de manera destacada la influencia del estado de polarización (SOP) en el rendimiento de enfoque, las paredes de separación entre dos nanorings adyacentes están diseñadas para ser de 100 nm, mucho más grandes que 2 δ _m para eliminar el efecto de acoplamiento.

El esquema del NRPL diseñado se muestra en la Fig. 2, y se incluye un número total de 32 nanorings concéntricos para reconstruir el frente de onda. El ancho del nanorreado para la modulación de fase deseada varía de 10 a 100 nm. La distancia focal deseada f ₀ es 1300 nm (2 λ ₀ ). Para utilizar de manera eficiente el modelo de guía de ondas MIM, el diámetro mínimo del nanorrenamiento más interno se establece en 800 nm. Además, para evitar el desplazamiento focal como se discutió en nuestro trabajo anterior [15], la diferencia de fase total es tan grande como 10π, con una apertura numérica predicha (NA) de 0.96. Como resultado, el límite de difracción de Rayleigh teórico, calculado por 0,61 λ ₀ / NA [31], es 413 nm (~ 0,64 λ ₀ ).

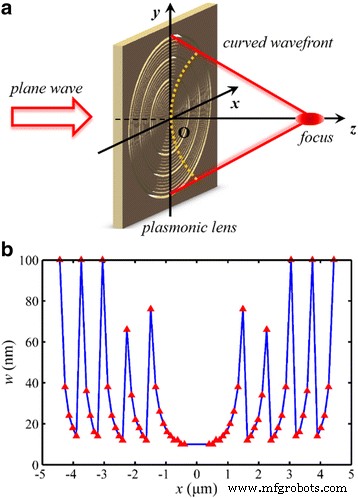
Esquema del NRPL. un La luz incidente normalmente ilumina la lente. b Parámetros estructurales de la lente. Los valores de las coordenadas de los triángulos rojos representar el radio r y ancho w de la nanoring correspondiente

Para investigar las influencias SOP de la luz incidente en las distribuciones de intensidad espacial, especialmente el rendimiento de enfoque, el NRPL diseñado se iluminó con luz polarizada lineal, circular, azimutal y radial, respectivamente. Todos los casos fueron calculados por las simulaciones numéricas FDTD. Según la óptica matricial, las diferentes luces polarizadas pueden describirse mediante los formalismos matriciales de Jones, y se aplicó la expresión matricial correspondiente para definir la luz incidente. El límite del modelo fue una capa perfectamente emparejada (PML) con un número de capa de 12. Para equilibrar la precisión computacional y el consumo de memoria en las simulaciones, el tamaño de malla se estableció en 10 nm en la región de salida y 5 nm alrededor de la región focal.

Resultados

I Polarización lineal

Para la luz polarizada linealmente, el SOP es espacialmente homogéneo y, en este caso, la dirección del vector eléctrico es paralela a la x eje. Cuando la luz ilumina el NRPL, existen dos focos, que se distribuyen a 400 nm entre sí en el campo eléctrico total | E | ² como se presenta en la Fig. 3. Aunque los anchos completos a la mitad del máximo (FWHM) de ambos son 210 nm (~ 0.32 λ ₀ ) en el plano focal, el resultado de la simulación indica que la distribución de intensidad es aparentemente diferente del diseño basado en la teoría de reconstrucción del frente de onda donde debería haber un foco de tipo circular exactamente en el z eje (también llamado eje óptico).

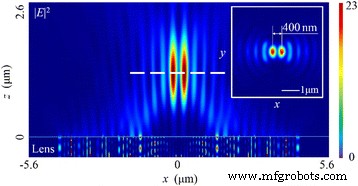
Patrón de distribución de intensidad del campo eléctrico total | E | ² en el caso de luz incidente polarizada linealmente. El recuadro muestra el patrón de intensidad en el plano focal. La distancia focal es de 1215 nm (una desviación del 6,54%). Los FWHM de ambos focos son ~ 0.32 λ ₀ , con 400 nm de distancia entre sí, y la profundidad de enfoque (DOF) es ~ 1,68 λ ₀

Para analizar las diferencias entre la simulación y el diseño teórico, se investigan las distribuciones de intensidad de los componentes del campo eléctrico. Como se presenta en la Fig.4, aparece un foco de forma elíptica y el FWHM en x- y y- la dirección es 220 nm (~ 0.34 λ ₀ ) y 457 nm (~ 0,70 λ ₀ ), respectivamente. Este patrón concuerda bien con los resultados experimentales de la Ref. [18] donde se aplicó la misma luz polarizada. Sin embargo, la simulación muestra que el patrón de distribución de | E | ² es similar al patrón del componente longitudinal | E _z | ² que ocupa el 79,8% del total de energía eléctrica. Por tanto, la diferencia se atribuye principalmente a la extraordinaria distribución de | E _z | ² .

Distribución de intensidad del componente transversal | E _r | ² en el plano focal. El recuadro muestra el enfoque de forma elíptica. La distancia focal es de 1425 nm (una desviación del 9,62%). | E _r | ² ocupa el 20,2% de la energía eléctrica total. El DOF es ~ 1,41 λ ₀

Este fenómeno puede explicarse en última instancia por la propiedad de transmisión del NRPL. Por un lado, la excitación de los SPP en las interfaces de metal y dieléctrico generalmente depende de la dirección de polarización local de la luz incidente. Las ondas eléctricas transversales (TE) no pueden contribuir a la excitación. Por otro lado, debido a la estructura de sublongitud de onda de la guía de ondas MIM, solo las ondas SP pueden propagarse a través de esta lente [32]. Con la simetría rotacional de la lente, el componente magnético transversal local (TM) cambia con el ángulo azimutal θ en la forma cosinoidea. Por lo tanto, como se muestra en la Fig. 5a, la distribución de intensidad de | E | ² , que está justo por encima de la superficie del extremo de la lente, se concentra cerca de y =0 región (−π / 4 < θ <Π / 4). En consecuencia, los vectores de Poynting se propagan a lo largo de la dirección radial en la superficie del extremo, como se presenta en la Fig. 5b. Por lo tanto, la dirección del vector de E es básicamente paralelo al eje óptico, que forma el contenido principal de E _z . Debido a la interferencia simétricamente constructiva, aparecen dos focos en el plano focal en lugar de un foco de tipo circular.

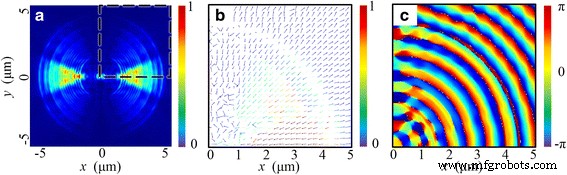
Las propiedades de distribución del campo eléctrico en la sección transversal están a solo 50 nm por encima de la superficie del extremo de la lente. un Distribución de intensidad normalizada de | E | ² . b La distribución del vector de Poynting dentro de la línea discontinua región en a. c La distribución de fase correspondiente de E _z

II Polarización circular

Como el estado de la luz polarizada circularmente cambia periódicamente con el tiempo, los resultados simulados son la distribución de campo promediada en el tiempo. Cuando la lente se ilumina con esta luz polarizada, se forma un foco en forma de rosquilla en | E _z | ² . Como se muestra en la Fig. 6a, la distancia focal en este campo es 1185 nm, mostrando una desviación del 8.85% del valor diseñado. El ancho de la rosquilla es 210 nm (~ 0.32 λ ₀ ) y el radio es de 400 nm. La profundidad de enfoque (DOF) es ~ 1,65 λ ₀ . El peso de | E _z | ² es el 80,6% de la energía eléctrica total. Además, en | E _r | ² , la superposición en el dominio espacial genera un foco circular con la distancia focal de 1405 nm (una desviación del 8.08%). El FWHM es 295 nm (~ 0.45 λ ₀ ) en este campo, y el DOF es ~ 1,68 λ ₀ . Además, ambos patrones de distribución en r-z avión se parecen a los del x - z plano en el caso de la luz incidente polarizada linealmente. Teniendo en cuenta el componente del campo eléctrico radial, el FWHM se puede reducir a 222 nm (~ 0.34 λ ₀ ).

Patrones de distribución de intensidad de | E _z | ² y | E _r | ² en r-z plano en el caso de luz polarizada circularmente. un En | E _z | ² , el FWHM, DOF y la distancia focal es ~ 0.32 λ ₀ , ~ 1,65 λ ₀ y 1185 nm, respectivamente. b En | E _r | ² , el FWHM, DOF y la distancia focal es ~ 0.45 λ ₀ , ~ 1,68 λ ₀ y 1405 nm, respectivamente

III Polarización azimutal

Para la luz incidente polarizada azimutalmente, los vectores eléctricos son perpendiculares a la dirección radial, que son paralelos a la interfaz oro / vacío del NRPL. A medida que la luz polarizada azimutalmente ilumina la lente, las ondas TE locales no logran excitar los SPP en la interfaz. Así, la distancia de transmisión en nanorings es proporcional a sus anchos como se presenta en la Fig. 7. Dado que tanto la estructura como la iluminación son de simetría rotacional, solo se muestran la mitad del patrón de distribución de intensidad y la estructura del NRPL. La luz transmitida puede despreciarse y no hay un foco distinto en la región de salida.

Patrón de distribución de intensidad en la región de la lente y su vista en sección transversal. La distancia de transmisión de las ondas no SP en nanorings es proporcional al ancho de la rendija

Polarización radial IV

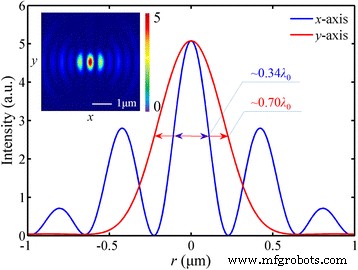
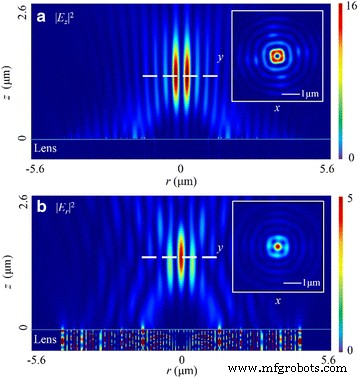
Correspondiente a la luz polarizada azimutalmente, la luz polarizada radialmente puede considerarse como la onda TM local, y esta propiedad de polarización coincide con la condición de excitación de los SPP, lo que contribuye a una mayor intensidad máxima en el foco. En campo eléctrico total E , la intensidad máxima es cinco veces mayor que la de la luz incidente polarizada linealmente. Además, hay un foco de forma circular con 276 nm (~ 0.42 λ ₀ ) FWHM en | E | ² , como se muestra en la Fig. 8. La distribución de intensidad simulada es muy similar a la capacidad de enfoque de la lente refractiva de alta NA [33]. Además, este rendimiento de enfoque aún depende de | E _z | ² , que ocupa el 82,0% del total de energía eléctrica.

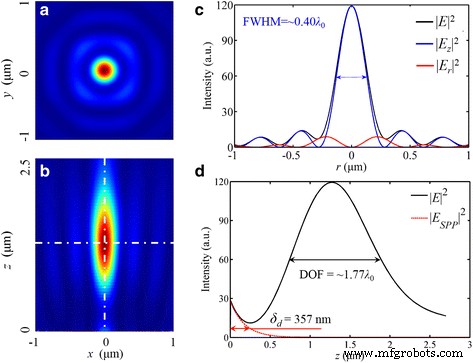
Distribución de intensidad de | E | ² en el caso de luz incidente polarizada radialmente. un , b La distribución en el plano focal y en x - z sección transversal. c El perfil de intensidad en la dirección radial. d El perfil de intensidad a lo largo del eje óptico donde la línea sólida negra es la distribución total de la intensidad del campo eléctrico en la simulación y la línea discontinua roja es la curva calculada de SPP. La distancia focal es de 1275 nm (una desviación del 1,92%). El FWHM de | E | ² y | E _z | ² es 272 nm (~ 0.42 λ ₀ ) y 260 nm (~ 0,40 λ ₀ ), respectivamente. El DOF es ~ 1,77 λ ₀

A diferencia de los casos anteriores, hay un foco de forma circular en | E _z | ² . Además, este componente también determina el patrón de distribución en | E | ² . Como se presenta en la Fig. 9a, el FWHM en | E _z | ² es de 260 nm (~ 0.40 λ ₀ ) que está cerca de la de la línea focal en el caso de PL basado en nanoslit [16]. En particular, la distancia focal es de 1275 nm. Comparado con el valor diseñado, el error relativo se reduce al 1,9%. Sin embargo, la distancia focal es 1455 nm (una desviación del 11,2%) en | E _r | ² . Como se presenta en la Fig. 9b, hay un foco en forma de rosquilla con un ancho de 227 nm (~ 0.35 λ ₀ ) en este campo. El DOF es ~ 1,60 λ ₀ .

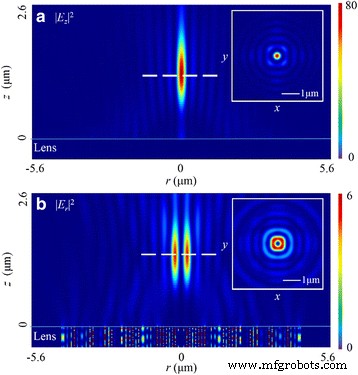
Patrones de distribución de intensidad de | E _z | ² y | E _r | ² en r-z plano en el caso de luz radialmente polarizada. un | E _z | ² patrón en el r-z avión. El recuadro muestra un foco de forma circular en el plano focal. b La transversal | E _r | ² patrón en el r-z avión. El recuadro muestra un enfoque en forma de rosquilla en el plano focal

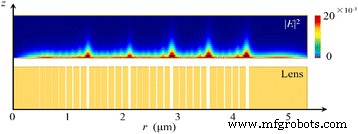
Se investiga el retardo de fase de las ondas SP en nanorings, como se presenta en la Fig. 10. La simulación indica que la modulación de fase está dramáticamente influenciada por los parámetros estructurales del NRPL y los retardos de fase simulados entre la superficie incidente y la superficie de salida son básicamente idéntico a los valores calculados basados ​​en la Ec. (2). En la superficie del extremo de la lente, las ondas SP aún se propagan a lo largo de la dirección radial y hay un punto caliente en el centro de la superficie, cuya intensidad es una quinta parte de la intensidad del enfoque. La interferencia constructiva de las ondas SP, con la distribución simétrica rotacional, construye las ondas que se propagan y realiza el foco de forma circular en el campo cuasi-lejano.

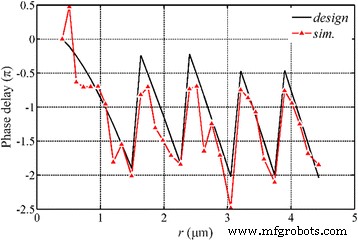
Análisis de fase del NRPL bajo la luz incidente polarizada radialmente

Discusiones

I Capacidad de superenfoque de los NRPL

A medida que se aplican las luces incidentes con diferentes SOP, incluidas las polarizaciones lineal, circular y radial, se pueden realizar los focos de límite de sub-difracción. Aunque la forma del foco está influenciada por el SOP, los tamaños característicos de estos focos superan el límite de difracción de Rayleigh (413 nm). Los resultados de la simulación demuestran con éxito la capacidad de superenfoque del NRPL, y la distribución de intensidad en el plano focal es similar a la función de Bessel que se utiliza para describir el haz sin difracción.

Para el caso de la luz incidente polarizada radialmente, como un ejemplo que se muestra en la Fig.11, la distribución de intensidad en | E _z | ² es idéntica a la función de Bessel de orden cero J ₀ ( K _spp ⋅ n ⋅ r ), donde n y r es el índice de refracción del medio ambiental y la distancia radial al eje óptico, respectivamente. El FWHM del foco es ligeramente mayor que el tamaño del lóbulo principal calculado con J ₀ . En particular, las simulaciones indican que el haz sin difracción se puede realizar en el campo cuasi lejano. Las ondas SP, como una especie de onda evanescente, disminuyen exponencialmente cuando se propagan lejos de la superficie de salida, y la distancia de propagación en el vacío se puede calcular mediante [30]:

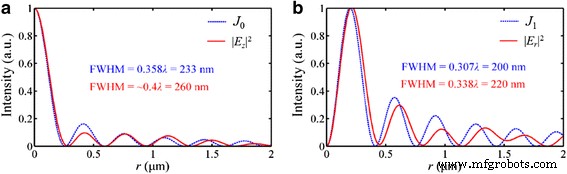
Perfiles de intensidad del NRPL en el plano focal bajo la luz incidente polarizada radialmente. un La distribución de | E _z | ² se asemeja a la función de Bessel de orden cero J ₀ . b La distribución de | E _r | ² se asemeja a la función de Bessel de primer orden J ₁

$$ {\ delta} _d =\ frac {1} {k_0} {\ left | \ frac {\ mathrm {Re} \ left ({\ varepsilon} _m \ right) + {\ varepsilon} _d} {{\ varepsilon_d } ^ 2} \ right |} ^ {\ frac {1} {2}} $$ (4)

donde ε _d y ε _m son la permitividad del dieléctrico y del metal, respectivamente. Por lo tanto, δ _d es 357 nm, lo cual es consistente con la simulación que se muestra en la Fig. 8d. Por lo tanto, la intensidad de las ondas SP en el foco puede despreciarse en la región de casi campo lejano.

II Forma de enfoque

Modulando el SOP, los focos de forma elíptica, circular y de rosquilla se pueden realizar en el plano focal, como se presenta en la Fig. 12. El fenómeno se atribuye al tamaño focal de sublongitud de onda, y no podemos realizar el tipo circular enfoque en campos eléctricos y magnéticos al mismo tiempo. Por lo tanto, se realiza un enfoque de tipo rosquilla en los campos magnéticos (o eléctricos), mientras que se logra un enfoque de tipo circular en el campo correspondientemente eléctrico (o magnético). Particularmente, debido a que no hay un campo magnético longitudinal, la distribución de intensidad de | H | ² es el mismo que el patrón de | E _r | ² . Además, | E _z | ² ocupa alrededor del 80.0% de la energía eléctrica total y la escala no se ve afectada por los SOP de la luz incidente.

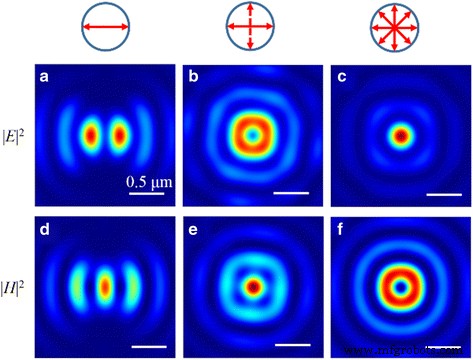
Los patrones de intensidad normalizados del campo eléctrico | E | ² y campo magnético | H | ² en el plano focal cuando el NRPL está iluminado por la luz polarizada. un | E | ² y d | H | ² Distribución con luz incidente polarizada linealmente. b | E | ² y e | H | ² Distribución con luz incidente polarizada circularmente. c | E | ² y f | H | ² distribución con luz incidente polarizada radialmente

III Modulación de la distancia focal

La distancia focal simulada en diferentes casos es básicamente cercana a la posición deseada f ₀ (1300 nm), como se muestra en la Tabla 1. Pero nos damos cuenta de que la distancia focal en el campo transversal | E _r | ² es aproximadamente 200 nm más largo que el del campo longitudinal | E _z | ² , independientemente del SOP de la luz incidente y la desviación comúnmente existe.

En teoría, la teoría de la reconstrucción del frente de onda es adecuada para diseñar el NRPL con una distancia focal arbitraria desde el campo cercano a la región del campo lejano. Sin embargo, si la distancia focal real de una lente plasmónica diseñada concuerda bien con la distancia focal diseñada depende de la diferencia de fase total de la lente. La desviación puede atribuirse a la distinción entre el enfoque de tipo amplitud y el enfoque de tipo fase [34]. Debido a que la modulación de fase en la guía de ondas MIM apunta al componente radial, la distancia focal en | E _r | ² puede ser modulado por la teoría de la reconstrucción del frente de onda, cuando se satisface la diferencia de fase total de al menos 2π [15]. Para el componente longitudinal, una diferencia de fase total mayor (> 10π) es ventajosa para la consistencia. Como se muestra en la Fig.13, cuando la diferencia de fase aumenta de 2π a 16π, correspondientemente el NA de 0,75 a 0,96, el foco de tipo amplitud en | E _z | ² moves from the output surface of the lens to the desired position. As the intensity distribution of |E | ² is decided by |E _z | ² , the NA can dramatically influence the focal length in the total electric field. However, the change of the focal length in |E _z | ² decreases gradually, along with the increase of the total phase difference. On the other hand, the position of the phase-type focus in |E _r | ² is relatively stable. When the NRPL with a high NA is applied, there is still a deviation in focal length derived based on the intensity distribution of |E _x | ² and |E _z | ² , and the deviation almost keeps invariable. Therefore, the focal length of the NRPLs can be effectively controlled by the phase modulation and structural optimization, though the same focal length cannot be achieved in the transverse and longitudinal component fields.

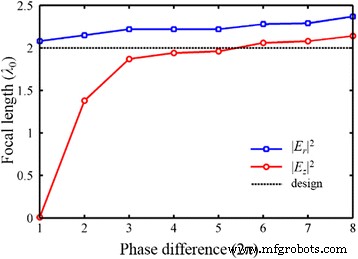
The focal length of the NRPL with the increase of total phase difference from 2π to 16π

IV Focusing Performace in the Non-Coaxial Situation

The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x eje. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ ₀ , respectively. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.

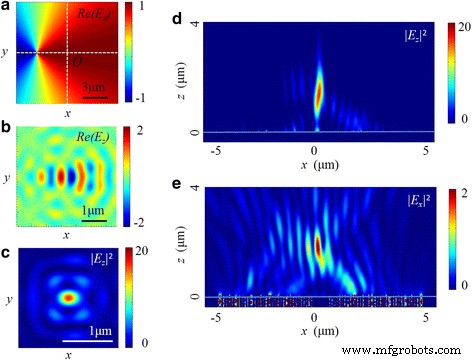
The intensity distribution of the NRPL in the non-coaxial situation. un The real part of E _x of radially polarized incident light. b , c The distribution of Re(E _z ) and |E _z | ² in the focal plane. d , e The distribution of |E _z | ² and |E _x | ² in the x-z plane

The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.

Conclusions

In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.

Abbreviations

DOF:

Depth of focus

FDTD:

Finite-difference time-domain

FWHM:

Full-width at half maximum

MIM:

Metal-insulator-metal

NRPL:

Nanoring-based plasmonic lenses

PML:

Perfectly matched layer

SOP:

State of polarization

SPPs:

Surface plasmon polaritons

TE:

Transverse electric

TM:

Transverse magnetic

Compuestos de grafeno y polímeros para aplicaciones de supercapacitores:una revisión Desentrañar la evolución morfológica y la cinética de grabado de nanocables de silicio poroso durante el grabado químico asistido por metales