Nanohélice de doble puerta como una nueva superrejilla binaria ajustable
Resumen
En teoría, investigamos el problema de un electrón confinado a una nanohélice entre dos puertas paralelas modeladas como cables cargados. El sistema de nanohélice de doble puerta es una superrejilla binaria con propiedades altamente sensibles a los voltajes de la puerta. En particular, la estructura de bandas exhibe cruces de bandas de energía para ciertas combinaciones de voltajes de puerta, lo que podría conducir a fenómenos cuasi relativistas similares a los de Dirac. Nuestro análisis de las transiciones ópticas inducidas por luz polarizada lineal y circularmente sugiere que una nanohélice de doble puerta se puede utilizar para aplicaciones optoelectrónicas versátiles.
Introducción
Desde los gasterópodos en espiral fosilizados que el primer autor recopiló con entusiasmo en su infancia, hasta la estructura entrelazada del ADN que sin duda alguna vez definió a esas criaturas prehistóricas, la geometría de la hélice prevalece en toda la naturaleza [1]. Inspirándose en las complejas funcionalidades atribuidas a las formas de biomoléculas naturales [2-6], se espera que otros sistemas que posean geometrías helicoidales adecuadas para la nanotecnología produzcan una física rica y contribuyan a nuevas aplicaciones. Durante las últimas tres décadas, el progreso notable en las técnicas de nanofabricación ha llevado a la realización de nanohelices en una serie de sistemas diferentes, incluidos InGaAs / GaAs [7], Si / SiGe [8], ZnO [9-11], CdS [ 12], SiO 2 / SiC [13, 14] y carbono puro [15-20], así como semiconductores II-VI y III-V [21] (para conocer el estado actual de la técnica, véanse las Refs. [21-26]). En consecuencia, se espera una plétora de fenómenos en tales estructuras que van desde propiedades de transporte exóticas como bombeo de carga cuantificado topológico [27, 28], superconductividad [29] y filtrado de espín [30-32], hasta electrónica extensible molecular y nanomecánica [33, 34] debido a efectos piezoeléctricos [35], aplicaciones de detección [36, 37], almacenamiento de energía [38] e hidrógeno [39] y transistores de efecto de campo [40, 41].
La fascinación por los dispositivos basados en nanohélice proviene en última instancia de la periodicidad inherente codificada en la topología de la estructura de la hélice. En particular, someter una nanohélice a un campo eléctrico transversal (normal al eje de la hélice) da lugar a un comportamiento de superrejilla, como la dispersión de electrones de Bragg en un potencial superperiódico, lo que lleva a una división de energía en el borde de la zona de Brillouin de la superrejilla entre los estados más bajos sintonizables linealmente por el campo eléctrico [42, 43]. Este comportamiento puede resultar en oscilaciones de Bloch y conductancia diferencial negativa [44, 45], y puede enfatizar el transporte de espín polarizado a través de hélices [31, 46], así como producir una mejora del dicroísmo circular útil en aplicaciones quiropticas nanofotónicas [47]. Este sistema constituye una superrejilla unaria y abre aún más la posibilidad de utilizar nanohelices como diodos de túnel o diodos de Gunn para multiplicación de frecuencia, amplificación y generación o absorción de radiación en el rango de terahercios elogiado [48-51]. Mientras que la superrejilla prototípica generalmente se realiza en heteroestructuras de capas semiconductoras alternas con diferentes intervalos de banda intrínsecos, los parámetros de la superrejilla de nanohélice están completamente controlados por el campo externo. Por el contrario, las formas de los antiguos potenciales de superrejilla convencionales son específicas de la heteroestructura y, aunque robustas, ofrecen una capacidad limitada de manipulación en el curso de su explotación sin el uso de grandes campos externos. Por lo tanto, el atractivo de utilizar nanohelices como superredes en lugar de esto radica en su mayor capacidad de sintonización.
Por otro lado, con superredes semiconductoras de heteroestructura (o de hecho estructuras de superrejilla fotónica [52-55] y átomos fríos en redes ópticas [56, 57]) se pueden crear celdas unitarias de superrejilla más complicadas más allá del pozo cuántico simple que es inducido por el campo eléctrico a lo largo de la hélice. Incluso la extensión a una superrejilla binaria [58-60] (en la que la celda unitaria se distingue por dos pozos y / o barreras cuánticas diferentes) promete una rica gama de física como las oscilaciones de Bloch-Zener [61], que a su vez pueden contribuir a aplicaciones de interferómetro y divisor de haz sintonizable [62]. Por lo tanto, sería muy deseable combinar la capacidad de sintonización del campo externo de una superrejilla basada en nanohélice con la funcionalidad superior de una superrejilla binaria.
A continuación, describimos un sistema de este tipo, con una nanohélice colocada entre dos cables cargados con compuertas paralelas alineados con el eje de la hélice. Prevemos la aplicación de un campo eléctrico transversal adicional y teóricamente mostramos que el potencial controlable por puerta y campo constituye una superrejilla binaria a lo largo de la hélice unidimensional.
Métodos
Modelo teórico
Comencemos por estudiar el caso de una nanohélice circular semiconductora de un solo electrón con N giros de radio R , tono p y longitud total L = Np . La nanoestructura se coloca entre dos puertas paralelas modeladas como cables cargados con su eje helicoidal alineado a lo largo de la z eje y con eje y puertas que residen en el mismo plano como se muestra en la Fig. 1. Además, consideramos un campo eléctrico transversal externo normal al plano del eje de la puerta \ (\ mathbf {E} =E _ {\ bot} \ hat {\ mathbf {y}} \) que se puede usar para romper la simetría de reflexión del potencial sobre el plano con respecto al potencial debajo del plano. Trabajamos en coordenadas helicoidales descritas paramétricamente mediante r =( x, y , z ) =( R cos ( s φ ), R pecado ( s φ ), ρ φ ), donde la coordenada angular dinámica φ = z / ρ depende solo de la distancia a lo largo del eje de la hélice con ρ = p / 2 π y s =± 1 indica una hélice de mano izquierda o derecha, respectivamente. En este trabajo, consideramos una hélice zurda s =1. En el marco del modelo de masa efectiva, el espectro de energía ε ν del ν el eigenstado de un electrón en una hélice bajo la influencia de tales potenciales externos se encuentra a partir de la ecuación de Schrödinger:
$$ - \ thinspace \ frac {\ hbar ^ {2}} {2M ^ {*} \ rho ^ {2}} \ frac {d ^ {2}} {d \ varphi ^ {2}} \ psi _ {\ nu} + \ left [V_ {g} (\ varphi) + V _ {\ bot} (\ varphi) \ right] \ psi _ {\ nu} =\ varepsilon _ {\ nu} \ psi _ {\ nu} $$ (1 )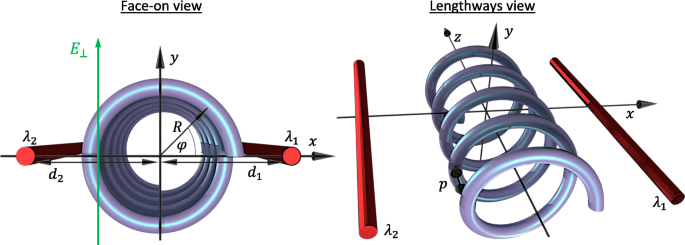
Diagrama de la geometría y los parámetros del sistema tanto desde la perspectiva frontal como longitudinal. R es el radio de la hélice y d 1 y d 2 son las distancias de los cables cargados desde el eje de la hélice con densidades de carga λ 1 y λ 2 , respectivamente. La coordenada espacial φ describe la posición angular en la hélice de frente y está relacionada con la z -coordinar a través de φ =2 π z / p con p el tono de la hélice. Un campo eléctrico transversal E ⊥ se aplica en paralelo a la y -eje
donde hemos renormalizado geométricamente la masa efectiva del electrón M e a M ∗ = M e (1+ R 2 / ρ 2 ) para expresar todo en términos de la coordenada a lo largo del eje de la hélice (recuerde que φ = z / ρ ) que es más conveniente para potenciales externos. Aquí, V ⊥ ( φ ) =- eE ⊥ R pecado ( φ ) es la contribución del campo eléctrico transversal dirigido a lo largo de y -eje tal que V ⊥ ( π / 2) <0. El potencial de las puertas es V g ( φ ) =- e [ Φ 1 ( φ ) + Φ 2 ( φ )] con el potencial electrostático sentido por un electrón a lo largo de la hélice debido a un cable individual cargado dado por Φ i ( φ ) =- λ i k ln ( r i / d i ). Aquí, yo =1,2 etiqueta los cables, λ i es la densidad de carga lineal en un cable y \ (k =1/2 \ pi \ tilde {\ epsilon} \) con \ (\ tilde {\ epsilon} \) la permitividad absoluta. La distancia perpendicular de una carga de prueba a un cable en particular está dada por \ (r_ {i} =[d ^ {2} _ {i} + R ^ {2} + 2 (-1) ^ {i} d_ {i } R \ cos (\ varphi)] ^ {1/2} \), con d i que denota la distancia correspondiente del alambre al eje de la hélice. Hemos definido el potencial inducido por puerta cero a lo largo del eje de la hélice. El potencial unidimensional total V T ( φ ) = V g ( φ ) + V ⊥ ( φ ) es claramente periódica V T ( φ ) = V T ( φ +2 π n ) con período 2 π en general (que corresponde al período de p con respecto a la coordenada z ). Este período es significativamente mayor que la distancia interatómica y da lugar a efectos típicos de superrejilla. Esta letra se diferencia de una nanohélice en un campo eléctrico transversal (que se puede reproducir con V T ( φ ) = V ⊥ ( φ ) aquí) principalmente manipulando la celda unitaria repetida de la superrejilla a través del potencial de doble puerta V g ( φ ). Tomando el límite p → 0, volvemos a la partícula en una imagen de anillo sujeta a dos puertas electrostáticas [63, 64]. Haciendo la aproximación R / d i ≪1, podemos expandir V g ( φ ) hasta segundo orden en cos ( φ ), y al transformar la Ec. 1 en forma adimensional llegamos a
$$ {\ begin {alineado} \ frac {d ^ {2} \ psi _ {\ nu}} {d \ varphi ^ {2}} + \ left [\ epsilon _ {\ nu} + 2A_ {g} \ cos ( \ varphi) + 2B_ {g} \ cos (2 \ varphi) + 2C _ {\ bot} \ sin (\ varphi) \ right] \ psi _ {\ nu} =0, \ end {alineado}} $$ (2)con las cantidades en unidades de la escala de energía \ (\ varepsilon _ {0} (\ rho) =\ hbar ^ {2} / 2 M ^ {*} \ rho ^ {2} \) definida como
$$ \ begin {array} {@ {} rcl @ {}} A_ {g} &=&\ beta \ frac {\ left (d_ {1} ^ {2} + R ^ {2} \ right)} { d_ {1} R} (1- \ gamma), \ qquad B_ {g} =\ frac {\ beta} {2} \ left (1+ \ frac {\ lambda_ {1}} {\ lambda_ {2}} \ gamma ^ {2} \ right), \\ C _ {\ bot} &=&e E _ {\ bot} R / 2 \ varepsilon_ {0} (\ rho), \ qquad \ qquad \ qquad \; \ epsilon _ {\ nu} =\ frac {\ varepsilon _ {\ nu}} {\ varepsilon_ {0} (\ rho)}. \ end {matriz} $$ (3)Aquí, \ (\ beta =ek d_ {1} ^ {2} R ^ {2} \ lambda _ {1} / 2 \ left (d_ {1} ^ {2} + R ^ {2} \ right) ^ {2} \ varepsilon _ {0} (\ rho) \) caracteriza la contribución de la puerta 1 mientras que el parámetro de asimetría \ (\ gamma =\ lambda _ {2} d_ {2} \ left (d_ {1} ^ {2 } + R ^ {2} \ right) / \ lambda _ {1} d_ {1} \ left (d_ {2} ^ {2} + R ^ {2} \ right) \) caracteriza la contribución relativa de la puerta 2 , con γ =1 correspondiente a contribuciones de puerta iguales al potencial (resultando en A g =0). Cabe señalar que la inevitable asimetría provocada por la dificultad para mantener d 1 = d 2 se puede compensar manipulando λ 1 y λ 2 . En esta carta, nos limitamos a considerar γ ≤1 (que es | Φ 1 |> | Φ 2 |) ya que el parámetro de asimetría que es mayor que la unidad se puede asignar a un sistema equivalente por debajo de la unidad mediante un simple intercambio de los índices que etiquetan las puertas y el correspondiente cambio de perspectiva φ → φ ± π . También consideraremos solo C ⊥ ≥0 debido a la simetría de C negativa ⊥ con respecto a dicha traslación de coordenadas en φ y A g ≥0, B g > 0 (es decir, solo densidades de carga positivas en los cables β > 0) ya que cualquier paisaje potencial con puertas cargadas negativamente se puede reproducir con la combinación correcta de parámetros de puertas cargadas positivamente. En la Fig. 2, graficamos el potencial adimensional V T ( φ ) / ε 0 ( ρ ), con la fuerza del π -componente de potencial periódico fijado en B g =0.2, para varias combinaciones de los parámetros de perturbación del período duplicado A g y C ⊥ . Vemos que el potencial externo total induce una superrejilla binaria a lo largo de φ , con un pozo cuántico doble (DQW) como celda unitaria resaltada en azul. Esto puede tomar formas cualitativamente diferentes manipulando las contribuciones de puerta relativas γ y campo eléctrico transversal E ⊥ . La celda unitaria es esencialmente un pozo único bajo contribuciones de puerta equivalentes ( γ =1) y sin campo eléctrico transversal E ⊥ =0 (como en la Fig. 2a para A g = C ⊥ =0). Arreglando E ⊥ =0, con una contribución de puerta 1 más fuerte ( γ <1), la celda unitaria se convierte en un DQW con mínimos de pozo diferentes y máximos de barrera degenerados (Fig. 2b donde A g =0.1 y C ⊥ =0). Por el contrario, mantener los mínimos DQW degenerados y manipular las dos barreras potenciales entre sí requiere contribuciones de puerta simétricas ( γ =1) en un campo eléctrico distinto de cero E ⊥ ≠ 0 (Fig. 2c con A g =0 y C ⊥ =0,1). Combinando contribuciones de puerta asimétricas ( γ <1) con E ⊥ ≠ 0 produce un DQW con diferentes mínimos de pozo de potencial y diferentes barreras (como se ve en la Fig. 2d donde ambos A g = C ⊥ =0,1). Esto conduce a un comportamiento rico y cualitativamente diferente, como veremos en las siguientes secciones.
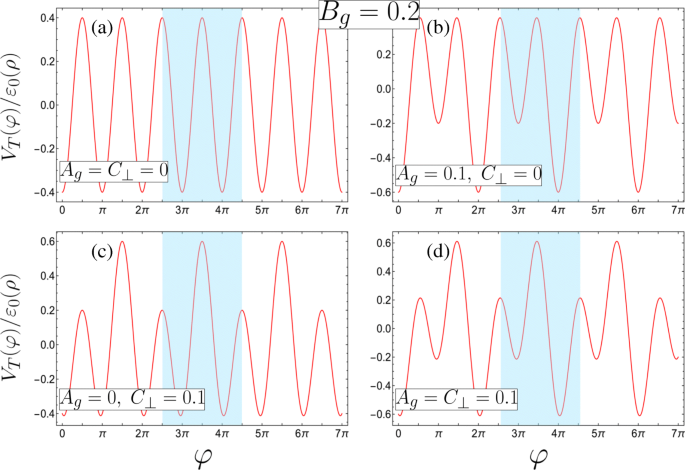
Las cuatro posibles configuraciones de potencial de superrejilla con las celdas unitarias resaltadas en azul (definidas en términos de los parámetros adimensionales, consulte la Ec. 3 para conocer los requisitos correspondientes de los parámetros físicos, y todas con B g =0,2). un Una superrejilla unaria con mínimos y máximos degenerados en la celda unitaria ( A g = C ⊥ =0). b - d Superredes binarias formadas a partir de b un DQW asimétrico con mínimos diferentes y simetría de reflexión interna sobre cualquiera de los mínimos debido a máximos degenerados ( A g =0.1, C ⊥ =0), c un DQW simétrico con mínimos degenerados solamente ( A g =0, C ⊥ =0.1) o d un DQW asimétrico con diferentes mínimos y máximos ( A g = C ⊥ =0.1)
Soluciones como una matriz infinita
Soluciones a Eq. 2 se puede encontrar en términos de las funciones de Bloch
$$ \ psi_ {n, q} (\ varphi) =(2 \ pi N \ rho) ^ {- \ frac {1} {2}} e ^ {iq \ varphi} \ sum_ {m} c ^ {( n)} _ {m, q} e ^ {im \ varphi}, $$ (4)donde el q = k z ρ es la forma adimensional del cuasimomento k del electrón z a lo largo del eje de la hélice, n indica la subbanda, y el prefactor surge de la normalización en términos de φ :\ (\ rho \ int _ {0} ^ {2 \ pi N} | \ psi _ {n, q} (\ varphi) | ^ {2} d \ varphi =1 \). Hacemos uso de la ortogonalidad de las funciones exponenciales multiplicando la expresión resultante por \ (e ^ {im ^ {\ prime} \ varphi} / 2 \ pi \) e integrando con respecto a φ , donde m ′ es un número entero, de modo que llegamos a un conjunto infinito de ecuaciones simultáneas para los coeficientes \ (c ^ {(n)} _ {m, q} \),
$$ {\ begin {alineado} &\ left [(q + m) ^ {2} - \ epsilon_ {n} \ right] c ^ {(n)} _ {m} - \ left (A_ {g} - i C _ {\ bot} \ right) c ^ {(n)} _ {m-1} - \ left (A_ {g} + i C _ {\ bot} \ right) c ^ {(n)} _ {m +1} \\ &\ quad- B_ {g} \ left (c ^ {(n)} _ {m + 2} + c ^ {(n)} _ {m-2} \ right) =0, \ fin {alineado}} $$ (5)donde para mayor claridad el q -se eliminó la notación de subíndice, ε n, q ≡ ε n y \ (c_ {m} ^ {(n)} \ equiv c_ {m, q} ^ {(n)} \). La ecuación 5 representa una matriz penta-diagonal infinita en la que es evidente que el sistema es periódico en q , y podemos restringir nuestras consideraciones a la primera zona de Brillouin definida por - 1 / 2≤ q ≤1 / 2. En ausencia del potencial de superrejilla A g = B g = C ⊥ =0, los valores propios se enumeran mediante m dado por ε m =( m + q ) 2 y reconocemos a m ser el número cuántico de momento angular asociado con un electrón libre en una hélice. Vemos en la Ec. 5 que cuando A g = C ⊥ =0 solo estados con Δ m =± 2 se mezclan, mientras que la formación de una celda unitaria DQW con diferentes mínimos de pozo o barreras, se logra a través de A g ≠ 0 y / o C ⊥ ≠ 0, también mezcla estados con Δ m =± 1. Curiosamente, el sistema de un electrón en una hélice bajo un potencial transversal externo (que varía en una revolución de la hélice) es matemáticamente equivalente a un electrón en un anillo cuántico atravesado por un campo magnético y sujeto a un potencial con la misma forma funcional variando a lo largo de la coordenada angular; p.ej. ver Ref. [65–67] o compare, por ejemplo, las Refs. [42-45] con [68-70]. Para un anillo, el papel que juega q aquí es absorbido por el flujo magnético. Por lo tanto, exactamente el mismo análisis en este trabajo es aplicable al problema de un anillo cuántico de doble compuerta [63-66], si el anillo fuera perforado por un flujo magnético.
Truncar y diagonalizar numéricamente la matriz correspondiente a la Ec. 5 proporciona la n th subbanda autoenergías ε n y coeficientes \ (c_ {m} ^ {(n)} \) para cada valor de q . Aplicamos un truncamiento en | m | =10, con la certeza de que cualquier aumento en el tamaño de la matriz no produce cambios apreciables en las subbandas más bajas.
Resultados y discusión
Estructura de banda de nanohélice de doble puerta
Trazamos en la Fig. 3 la dispersión de energía de las bandas más bajas para varias combinaciones de parámetros. Dependiendo de la forma de la superrejilla, encontramos una variedad notable en el comportamiento de dispersión, y para algunas combinaciones específicas de parámetros, descubrimos cruces de bandas de energía para subbandas particulares en el borde de la zona de Brillouin (Fig. 3a yc) o en la centro de la zona de Brillouin (Fig. 3b yd).
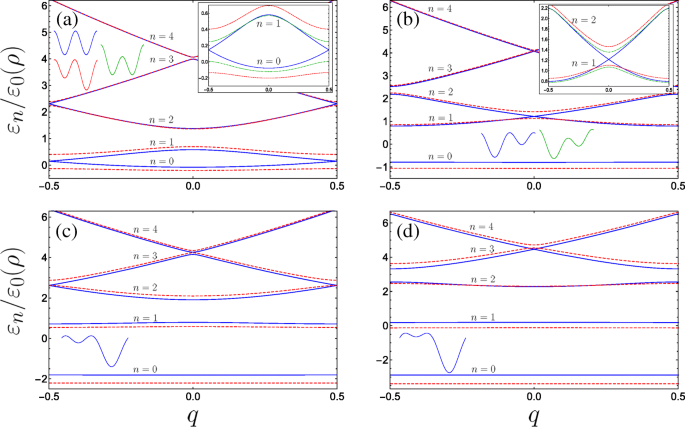
Estructura de banda para el sistema nanohélice de doble puerta para varias combinaciones de parámetros adimensionales (con B g =0.4 fijo en todo): a Gráficos A en azul sólido (rojo discontinuo) g =0 y C ⊥ =0 ( A g =0,2 y C ⊥ =0), el recuadro también traza el comportamiento de las dos subbandas inferiores sujetas al campo eléctrico transversal con A g =0 y C ⊥ =0,2 como la curva verde punteada con puntos. b Gráficos A en azul sólido (rojo discontinuo) g =0,63 y C ⊥ =0 ( A g =0,8 y C ⊥ =0) donde la curva azul representa el primer incidente de resonancia (ver texto) con bandas de energía cruzando en el centro de la zona de Brillouin, el recuadro compara el comportamiento de las dos subbandas excitadas inferiores con el caso donde A g =0,63 y C ⊥ =0,2 como la curva verde punteada con puntos. c Gráficos A en azul sólido (rojo discontinuo) g =1,26 y C ⊥ =0 ( A g =1,5 & C ⊥ =0) donde la curva azul representa el segundo incidente de resonancia con brechas de energía cerrándose en el borde del Brillouin para bandas más altas. d La tercera resonancia y los minigaps de subbanda superior se cierran en el centro, y el azul sólido (rojo discontinuo) es A g =1.9 & C ⊥ =0 ( A g =2.2 & C ⊥ =0). Las formas de las celdas unitarias están esbozadas, n enumera las bandas, y el eje de las inserciones es el mismo que el de los gráficos principales
Perturbación de período doble de campo bajo
Cuando A g = C ⊥ =0, la celda unitaria constituye dos pozos cuánticos equivalentes y, en consecuencia, la aparición de pares de bandas que se tocan en los bordes de la zona de Brillouin surge de forma natural. De hecho, tomar solo un pozo como celda unitaria reduce a la mitad el período de superrejilla y da como resultado una duplicación de la zona de Brillouin:1≤ q ≤1. Luego observaríamos el diagrama de bandas de superrejilla unaria habitual, en el que la banda prohibida entre el suelo y las primeras bandas en q =1 se da aquí a través de la banda prohibida entre n =1 y n =2 en q =0 y sería lineal en B g de la teoría de la perturbación. Aún así, presentamos una descripción de la estructura de la banda en | q | =1/2 en la imagen de celda unitaria DQW usando álgebra matricial en el Apéndice. Como se ve en el recuadro de la Fig. 3a, la introducción de cualquiera de los términos de potencial de período doble abre una brecha de banda en el borde de la zona de Brillouin. La celda unitaria de las contribuciones de puerta simétrica ( A g =0) conserva la forma de un DQW simétrico bajo la aplicación de un campo transversal C ⊥ perpendicular al eje hélice-puerta, con una barrera de potencial modificada con respecto a la otra (indicada por el boceto verde DQW en la Fig. 3a). Mientras C ⊥ abre una banda prohibida, la modificación de la dispersión es notablemente menos sensible que la de una magnitud similar de A aplicada g . Esto se ve en la banda prohibida más pequeña en | q | =1/2 para la línea verde punteada en el recuadro de la Fig. 3a (con A g =0 y C ⊥ =0,2) en comparación con el espacio más grande de la curva roja discontinua (que es para A g =0.2 y C ⊥ =0). Para enfatizar este comportamiento, la Fig. 4a traza el tamaño de la brecha de energía en | q | =1/2 entre las dos subbandas más bajas \ (\ Delta \ varepsilon _ {01} ^ {(q =1/2)} / \ varepsilon _ {0} (\ rho) \) para B g =0,25 en función de ambos C ⊥ (con A g =0) y A g (con C ⊥ =0), como curvas de puntos en verde y rojo, respectivamente. En campo eléctrico transversal cero y potenciales de puerta asimétricos ( C ⊥ =0 y A g ≠ 0), la celda unitaria es entonces un DQW asimétrico, aunque con simetría de reflexión interna sobre los mínimos de los pozos debido a las barreras equivalentes. Entonces podemos comprender la mayor sensibilidad de la banda prohibida para cambiar A g considerando las propiedades de la celda unitaria DQW aislada a partir de la cual se construye la superrejilla. Con A g = C ⊥ =0, en | q | =1/2 (los bordes de la zona de Brillouin), los estados de Bloch formados a partir del suelo y el primer estado excitado de la celda unitaria DQW aislada (ver el esquema azul y las funciones de onda que lo acompañan en la Fig. 4a) diferirán solo por un fase arbitraria. Esta situación corresponde a la curva de dispersión azul sin espacios de la Fig. 3a. Como se muestra esquemáticamente en la Fig. 4a a través del boceto DQW verde, C ⊥ reduce los máximos relativos de una de las barreras con respecto a la otra, mientras que los mínimos DQW permanecen degenerados. Como tal, el estado fundamental del DQW aislado solo se modifica por un ligero aumento en su distribución de probabilidad bajo la barrera de potencial más pequeña (produciendo solo una pequeña disminución de energía en comparación con el estado fundamental no perturbado), y el primer estado excitado permanece esencialmente sin cambios ya que su nodo se coloca debajo de la barrera y no es sensible a su variación. Los estados de Bloch en el borde de la zona de Brillouin que se construyen a partir de estos estados de tierra y primeros excitados difieren del caso no perturbado solo en la disminución reducida de la función de onda del estado de base debajo de la barrera más pequeña (compare el DQW verde con el DQW azul en Figura 4a). Cambiar A g manipula las posiciones relativas de los mínimos DQW mientras mantiene las barreras degeneradas. Las funciones de onda de los dos estados DQW aislados más bajos difieren considerablemente, el estado fundamental tiende hacia el estado fundamental localizado del pozo singular más profundo y el primer estado excitado tiende hacia el estado fundamental localizado del pozo menos profundo [71]. Mientras que la perturbación reduce la energía del estado fundamental, la energía del primer estado excitado aumenta comparativamente a medida que los mínimos del pozo menos profundo se desplazan hacia arriba con el aumento de A g , lo que da como resultado una mayor sensibilidad del tamaño de la banda prohibida con respecto a A g . En particular, una partícula en la subbanda terrestre se encuentra rápidamente confinada cerca del fondo del pozo de potencial más profundo al aumentar A g . Por lo tanto, la banda más baja se acerca a una banda plana sin dispersión más rápida que en el caso del campo transversal, lo que puede conducir a inestabilidades electrónicas y fuertes efectos de interacción que acompañan a la alta densidad de estados [72].
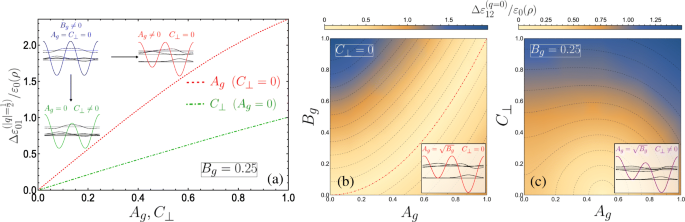
un Tamaño de la brecha de banda entre el suelo y las primeras subbandas en función de A g ( C ⊥ ) trazado como rojo punteado (verde punteado con puntos), aquí B g =0,25. Los diagramas indican la influencia de las diferentes perturbaciones en la celda unitaria aislada DQW y los estados propios. b - c El tamaño de la banda prohibida entre la primera y la segunda subbandas se indica mediante un gráfico de densidad 2D en función de; b A g y B g para C ⊥ =0 y c A g y C ⊥ con B fijo g =0,25. b Las curvas de nivel de isoenergía adyacentes indican una diferencia de 0.17, con un espacio cero dado por la línea roja discontinua para \ (A_ {g} =\ sqrt {B_ {g}} \), mientras que c la diferencia es 0,13 con espacio cero en el centro del contorno de semicírculo más pequeño (0,5,0). Los diagramas bosquejan el DQW aislado y los estados propios. La hibridación no ocurre entre las s -like y p -como estados de pozo individuales localizados resonantes en b , pero lo hace en c debido a que el campo eléctrico cambia una barrera con respecto a la otra
Cruces de bandas de energía
Es bastante notable ver que si mantenemos C ⊥ =0 y aumentar A g , mientras que inicialmente se eliminan todas las degeneraciones, las bandas posteriores de mayor energía se cruzan entre sí alternando entre el centro y el borde de la zona de Brillouin (observe el comportamiento de las curvas alternas de azul y rojo discontinuo que progresan desde la Fig.3a hasta la d). Físicamente, podemos entender la desaparición de la banda prohibida en términos de interacciones de las funciones de onda localizadas en la celda unitaria. Cuando el potencial DQW asimétrico es tal que el estado fundamental en el pozo menos profundo ( s -como orbital) resonante con el primer estado excitado en el pozo más profundo ( p -como orbital), en q =0 debido a la simetría de reflexión sobre el centro de cada pozo, las paridades opuestas de estos estados impiden el acoplamiento túnel habitual entre ellos y, en consecuencia, los estados excitados construidos a partir de estos orbitales coinciden (curvas azules en la Fig. 3b). Esto recuerda a los llamados s - p resonancias en redes ópticas [73, 74]. De la misma manera, si los parámetros son tales que el estado fundamental localizado en el pozo poco profundo resuena con un estado excitado en el pozo más profundo que tiene la misma paridad, entonces en | q | =1/2, la presencia de la fase de Bloch suprime por completo la hibridación habitual entre estos dos estados de pozos localizados adyacentes y la banda prohibida se cierra (como se muestra en la Fig. 3c para la resonancia del suelo con el segundo estado excitado). En el lenguaje de la dispersión del potencial periódico; la banda prohibida se cierra debido a la interferencia destructiva completa de las amplitudes de dispersión de Bragg de segundo orden del cos ( φ ) amplitudes de dispersión potenciales y de primer orden del cos (2 φ ) potencial [75–77].
Podemos mostrar cuantitativamente la existencia de cruces de bandas de energía (para campo eléctrico transversal cero) tanto en el centro como en el borde de la zona de Brillouin volviendo a la Ec. 2, que se reconoce como la ecuación de Whittaker-Hill cuando C ⊥ =0 [78]. Las funciones de Bloch Eq. 4 obedece las condiciones de contorno periódicas retorcidas ψ n, q ( φ +2 π ) =exp (2 π iq ) ψ n, q ( φ ). En particular, cuando q =0 soluciones formales de la ecuación. 2 son 2 π -periódico, mientras que cuando | q | =1/2 soluciones son 2 π -antiperiodic (y por lo tanto buscaremos 4 π -soluciones periódicas). Específicamente, Eq. 2 con C ⊥ =0 se puede asignar a la ecuación de Ince [79, 80], que se puede resolver casi exactamente, expresando la función de onda como el producto de la solución asintótica a la ecuación. 2 y una función desconocida \ (\ psi _ {n, q} (\ varphi) =\ exp \ left [-2 \ sqrt {B_ {g}} \ cos (\ varphi) \ right] \ Phi _ {n, q} (\ varphi) \), tal que
$$ \ frac {d ^ {2} \ Phi_ {n, q}} {d \ varphi ^ {2}} + \ frac {\ xi} {2} \ sin (\ varphi) \ frac {d \ Phi_ { n, q}} {d \ varphi} + \ frac {1} {4} \ left [\ eta_ {n, q} - p \ xi \ cos (\ varphi) \ right] \ Phi_ {n, q} =0, $$ (6)donde hemos definido los parámetros auxiliares \ (\ xi =8 \ sqrt {B_ {g}} \), η n, q =4 ε n, q +8 B g , \ (- p \ xi =8A_ {g} +8 \ sqrt {B_ {g}} \) y Φ n, q ( φ ) mantiene la periodicidad retorcida necesaria de cada solución (tenga en cuenta que aquí p es no el paso de la hélice). Además, como el potencial de superrejilla aquí es invariante bajo la transformación φ → - φ , las soluciones para q =0 y q =1/2 se puede separar en paridad par e impar, de modo que la siguiente serie trigonométrica
$$ \ Phi_ {n, 0} ^ {(e)} (\ varphi) =\ sum_ {l =0} a ^ {(n)} _ {l} \ cos (l \ varphi), $$ (7a ) $$ \ Phi_ {n, 0} ^ {(o)} (\ varphi) =\ sum_ {l =0} b ^ {(n)} _ {l + 1} \ sin [(l + 1) \ varphi], $$ (7b) $$ \ Phi_ {n, \ frac {1} {2}} ^ {(e)} (\ varphi) =\ sum_ {l =0} \ widetilde {a} ^ {( n)} _ {l} \ cos \ left [\ left (l + \ frac {1} {2} \ right) \ varphi \ right], $$ (7c) $$ \ Phi_ {n, \ frac {1} {2}} ^ {(o)} (\ varphi) =\ sum_ {l =0} \ widetilde {b} ^ {(n)} _ {l + 1} \ sin \ left [\ left (l + \ frac {1} {2} \ right) \ varphi \ right], $$ (7d)cubren las soluciones formales, y observamos que las soluciones para q =−1 / 2 son iguales que para q =1/2. Aquí, los superíndices e y o etiquetar las funciones como pares e impares, respectivamente, y n todavía se refiere a la n th subbanda, que también es la n el eigenstate para estos q especificados valores. Sustituyendo estos en Eq. 6 da como resultado relaciones de recursividad de tres términos para los coeficientes de Fourier. El q =0 rendimiento uniforme de la solución
$$ - \ eta_ {n, 0} ^ {(e)} a ^ {(n)} _ {0} + \ xi \ left (\ frac {p} {2} +1 \ right) a ^ {( n)} _ {2} =0, $$ (8a) $$ \ xi pa ^ {(n)} _ {0} + \ left (4 - \ eta_ {n, 0} ^ {(e)} \ derecha) a ^ {(n)} _ {2} + \ xi \ left (\ frac {p} {2} +2 \ right) a ^ {(n)} _ {4} =0, $$ (8b ) $$ {\ begin {alineado} &\ xi \ left (\ frac {p} {2} - l +1 \ right) a ^ {(n)} _ {2l-2} + \ left (4l ^ { 2} - \ eta_ {n, 0} ^ {(e)} \ right) a ^ {(n)} _ {2l} \\ &\ quad + \ xi \ left (\ frac {p} {2} + l +1 \ right) a ^ {(n)} _ {2l + 2} =0, \ qquad (l \ ge 2) \ end {alineado}} $$ (8c)y las relaciones de recursividad correspondientes para la solución impar de q =0 es
$$ (4 - \ eta_ {n, 0} ^ {(o)}) b ^ {(n)} _ {2} + \ xi \ left (\ frac {p} {2} +2 \ right) b ^ {(n)} _ {4} =0, $$ (9a) $$ {\ begin {alineado} &\ xi \ left (\ frac {p} {2} - l +1 \ right) b ^ { (n)} _ {2l-2} + \ left (4l ^ {2} - \ eta_ {n, 0} ^ {(o)} \ right) b ^ {(n)} _ {2l} + \ xi \ left (\ frac {p} {2} + l +1 \ right) b ^ {(n)} _ {2l + 2} \\ &=0. \ qquad (l \ ge 2) \ end {alineado} } $$ (9b)El q =1/2 solución uniforme da
$$ \ left [1 - \ eta_ {n, \ frac {1} {2}} ^ {(e)} + \ frac {\ xi} {2} (p + 1) \ right] \ widetilde {a} ^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{a}^{(n)}_{3}=0, $$ (10a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l +1)\widetilde{a}^{(n)}_{2l-1}+\left[(2l+1 )^{2} - \eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{a}^{(n)}_{2l+1}\\ &\ quad+ \frac{\xi}{2}(p+2l+3)\widetilde{a}^{(n)}_{2l+3}=0, \qquad (l \ge 1) \end{aligned} } $$ (10b)and the q =1/2 odd solution gives
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} -\frac{\xi}{2}(p+1) \right]\widetilde{b}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{b}^{(n)}_{3}=0 $$ (11a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l+1)\widetilde{b}^{(n)}_{2l-1}+\left[(2l+1)^{2} -\eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{b}^{(n)}_{2l+1}\\&\quad + \frac{\xi}{2}(p+2l+3)\widetilde{b}^{(n)}_{2l+3}=0. \qquad (l \ge 1) \end{aligned}} $$ (11b)Consider then Eqs. (8c) and (9b) for the q =0 solutions. The series solutions (7a) and (7b) can clearly be made to terminate if p is 0 or an even positive integer. The resulting polynomials are referred to as Ince polynomials. The remaining solutions for higher eigenvalues are simultaneously double degenerate and correspond to the energy crossings observed at q =0 for certain parameters. The existence of these degeneracies can be seen by looking at the diagonalizable matrices describing the recursion relations for a l y b l :
$$ \boldsymbol{\mathcal{A}} =\left[ \begin{array}{ccccc} 0 &\xi\left(\frac{p}{2} +1 \right) &0 &0 &\hdots \\ \xi p &4 &\xi\left(\frac{p}{2} +2 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \end{array} \right]\!, $$ (12)and
$$ \boldsymbol{\mathcal{B}} =\left[ \begin{array}{ccccc} 4 &\xi\left(\frac{p}{2} +2 \right) &0 &0 &\hdots \\ \xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} -2 \right) &36 &\xi\left(\frac{p}{2} +4 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \\ \end{array} \right]\! $$ (13)respectivamente. Either of the above tridiagonal matrices can be broken into tridiagonal sub-matrices if a leading off-diagonal matrix element is equal to zero, i.e. if p is an even number. The matrices will decompose into two tridiagonal blocks, one smaller finite matrix \(\boldsymbol {\mathcal {A}_{1}}\) (\(\boldsymbol {\mathcal {B}_{1}}\)) and a remaining infinite matrix \(\boldsymbol {\mathcal {A}_{2}}\) (\(\boldsymbol {\mathcal {B}_{2}}\)). From the theory of tridiagonal matrices the corresponding eigenvalue spectra for each matrix is then \(\eta (\boldsymbol {\mathcal {A}}) =\eta (\boldsymbol {\mathcal {A}_{1}}) \cup \eta (\boldsymbol {\mathcal {A}_{2}})\) and \(\eta (\boldsymbol {\mathcal {B}}) =\eta (\boldsymbol {\mathcal {B}_{1}}) \cup \eta (\boldsymbol {\mathcal {B}_{2}})\). The smaller finite matrices are analytically diagonalizable in principle, giving exact eigenvalues, and their corresponding finite length eigenvectors define the fourier coefficients yielding Ince polynomials via Eq. 7. We can see that for a given even integer p , the remaining infinite tridiagonal matrices are the same \(\boldsymbol {\mathcal {A}_{2}}=\boldsymbol {\mathcal {B}_{2}}\equiv \boldsymbol {\mathcal {D}}\) which results in the double degenerate eigenvalues. To be clear, we provide an example of when p =2 in the Appendix.
In the same way, when p is a positive odd integer the series solutions (7c) and (7d) can be made to terminate, and the matrices corresponding to \(\widetilde {a}_{l}\) and \(\widetilde {b}_{l}\) share eigenvalues resulting in the closing of higher subbands at the edge of the Brillouin zone q =± 1/2. From the definitions of the auxiliary parameters in Eq. 6, we have
$$ A_{g} =(p+1)\sqrt{B_{g}}, $$ (14)which defines the condition for exactly-solvable solutions for the lower lying solutions and simultaneously the existence of higher double degenerate eigenvalues above the p th subband, with p =0 or an even positive integer corresponding to crossings at the centre of the Brillouin zone, while crossings at the edge require p to be an odd positive integer. Figure 4b plots the size of the band gap between the first and second subbands \(\Delta \varepsilon _{12}^{(q=0)}/\varepsilon _{0}(\rho)\) as a function of A g y B g , with the dot-dashed red contour line corresponding to Eq. 14 for p =0. The schematic indicates the appropriate eigenstates of the isolated DQW at the p =0 resonance.
The application of a small transverse field C ⊥ breaks the reflection symmetry of the system, permitting hybridization of the localized well states of the isolated DQW which results in a significant change at points of degeneracy, as can be seen by comparing the schematic depicted in Fig. 4b with that in c (see also inset of Fig. 3b). We plot in Fig. 4c the behaviour of the band gap between the first and second subbands as a function of A g y C ⊥ . Here we see that the band gap is more sensitive to C ⊥ due to the significant change in the isolated DQW eigenstates by lowering one barrier with respect to the other. This behaviour is notably the converse of the parameter sensitivity for the band gap between the ground and first subbands. By degenerate perturbation theory, it can be shown that this induced band gap is linear in C ⊥ for the lowest crossing bands when p =0, and to higher order with increasing p . Finally, within the vicinity of the crossings, e.g. for small q about q =0 in Fig. 3a, the dispersions could be approximated as a quasi-relativistic linear dispersion yielding Dirac-like physics, which could permit superfluiditiy [81] for example. The advantage in using nanohelices lies in introducing such phenomena to portable nanostructure based devices, while also exhibiting unusual responses of the charge carriers to circularly polarized radiation [44, 45, 82–85] (or indeed magnetic fields [86, 87]) due to the helical spatial confinement.
Optical transitions
In order to understand how our double-gated nanohelix system interacts with electromagnetic radiation, we study the inter-subband momentum operator matrix element \(T^{g\rightarrow f}_{j} =\langle {f}|\boldsymbol {\hat {j}} \cdot \boldsymbol {\hat {P}}_{j} |{g}\), which is proportional to the corresponding transition dipole moment, and dictates the transition rate between subbands ψ f and ψ g . Here, \(\boldsymbol {\hat {j}}\) is the projection of the radiation polarization vector onto the coordinate axes (j =x,y , z ) and the respective self-adjoint momentum operators are [44, 45, 82–84]
$$ \boldsymbol{\hat{P}}_{x} =\boldsymbol{\hat{x}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\sin(\varphi)\frac{d}{d\varphi} + \frac{1}{2}\cos(\varphi) \right], $$ (15a) $$ \boldsymbol{\hat{P}}_{y}=-\boldsymbol{\hat{y}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\cos(\varphi)\frac{d}{d\varphi} - \frac{1}{2}\sin(\varphi) \right], $$ (15b) $$ \boldsymbol{\hat{P}}_{z}=-\boldsymbol{\hat{z}}\frac{i \hbar \rho}{\rho^{2} +R^{2}}\frac{d}{d\varphi}. $$ (15c)In terms of the dimensionless position variable φ , we are required to evaluate \(T^{g\rightarrow f}_{j} =\rho \int _{0}^{2\pi N}\psi _{f}^{\ast } P_{j} \psi _{g} d\varphi \), and upon substituting in from Eq. 4 we find
$$ {\begin{aligned} T^{g\rightarrow f}_{x} &=\frac{i \hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\ &\quad\left.-c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16a) $$ {\begin{aligned} T^{g\rightarrow f}_{y} &=\frac{\hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\&\left.\quad+c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16b) $$ T^{g\rightarrow f}_{z} =\frac{\hbar \rho}{\left(\rho^{2} + R^{2} \right)} \sum_{m} c_{m}^{\ast (f)} c_{m}^{(g)} (q+m). $$ (16c)We see from Eqs. 16a and 16b that light linearly polarized transverse to the helix axis couples coefficients with angular momentum differing by unity Δ m =± 1, whereas from Eq. 16c, linear polarization parallel to the helix axis couples only Δ m =0. In Fig. 5, we plot the absolute square of the momentum operator matrix element between the lowest three bands for linearly polarized light propagating perpendicular to the helix axis (i.e. with z -polarización). Initially, for A g =C ⊥ =0, transitions between the ground and first bands are forbidden (as is to be expected for a unit cell with two equivalent wells resulting in a doubling of the first Brillouin zone, so it is in fact the same band). As the strength of the doubled period potential A g is increased with respect to B g , transitions become allowed away from q =0 as can be seen from Fig. 5a (following behaviour from the dotted red curve through to the solid blue curve). The parameters are swept through a resonance as we go from the solid to the dashed blue curve, wherein the situation changes drastically. To understand this behaviour, we must consider the special case of q =0. As we traverse this resonance, the energy of the Bloch function with q =0 constructed from the first excited state of the deeper well in the DQW unit cell (p -like) passes below the Bloch function constructed from the ground state in the shallower well (s -like). Consequently, the parity with respect to φ (which is a good quantum number only for q =0 or |q |=1/2) of the two excited states is exchanged resulting in the rapid switch from forbidden to allowed at q =0, wherein the z -polarized inter-subband matrix element becomes non-zero due to the operator \(\boldsymbol {\hat {P}}_{z}\) (see Eq. 15c) now coupling the even ground state with the odd first excited state. We therefore see the opposite behaviour for transitions between the ground and second band in Fig. 5b about q =0. While initially increasing A g allows transitions at q =0 between the ground state and the second excited state when it is p -like, beyond resonance (when the order of the s -like and p -like excited states are swapped) transitions are suppressed. See for example Ref. [88] for a clear picture of this interchange between the ordering of the even and the odd parity excited states. For transitions between the first and second band (Fig. 5c), we observe a large transition centred about q =0 due to the lifting of the m =± 1 degenerate states of the field-free helix by the superlattice potential. The presence of symmetry-breaking C ⊥ ruins the pristine parities of the states at the centre of the Brillouin zone and all transitions are allowed, as shown in the insets of Fig. 5.
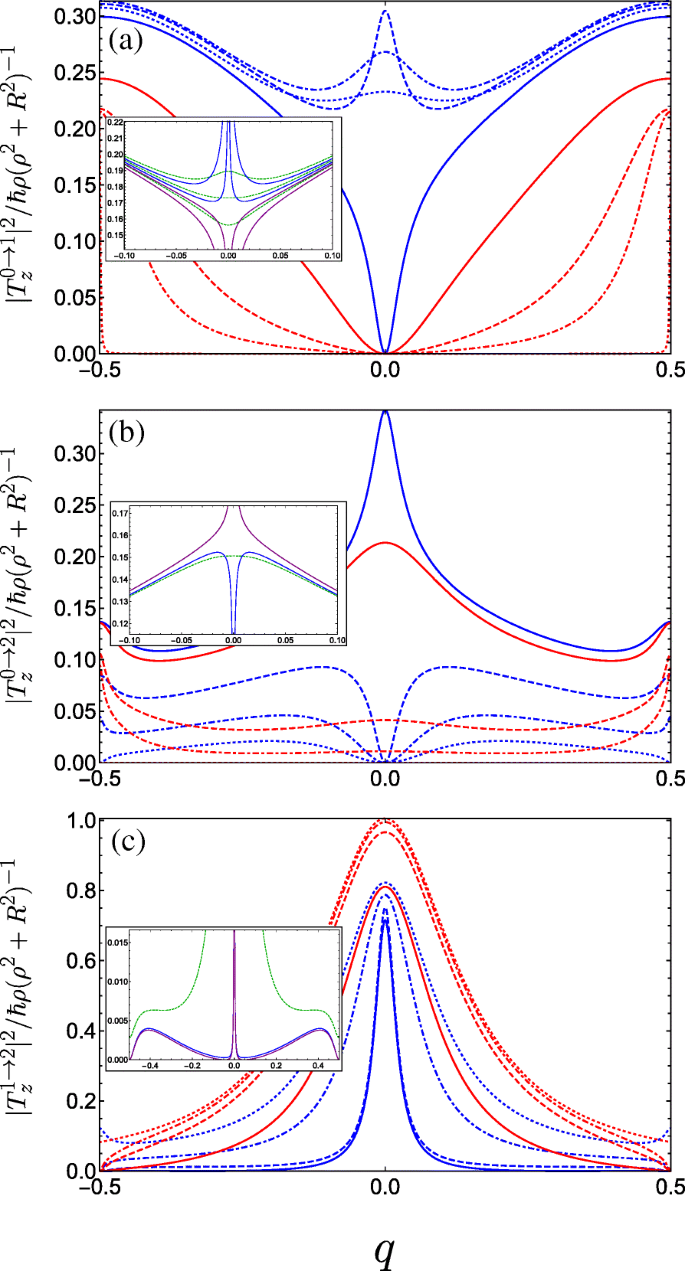
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by linearly z -polarized radiation and for a variety of parameter combinations spanning the first incident of resonance. The different blue curves keep A g =0.5 and C ⊥ =0 fixed and vary B g =0.1, 0.2, and 0.3 corresponding to dot-dashed, dashed, and solid. The different red curves keep B g =0.3 and C ⊥ =0 fixed while varying A g =0.05, 0.1 and 0.3 as dot-dashed, dashed, and solid, while the dotted blue (dotted red) plots the limiting case A g =0.5 &B g →0 (A g →0 &B g =0.3). un Transitions between the ground and first bands. The inset plots the behaviour for fixed A g =0.5 and changing B g crossing the resonant condition at B g =0.25 (see text) in a reduced q -range, ranging from upper blue B g =0.245, lower blue B g =0.249, upper purple B g =0.251, to lower purple B g =0.255. The dashed green curves are for small non-zero transverse field C ⊥ =0.05 ranging from B g =0.245 (upper curve) to B g =0.255 (lower curve) in increments of 0.05. b Plots transitions between the ground and second bands, the inset plots the behaviour close to resonance when A g =0.5; blue is B g =0.249, purple is B g =0.251, and dark green is at resonance with C ⊥ =0.05. c Plots transitions between the first and second bands, the parameters for the inset are the same as those in (b )
In Fig. 6, we plot the absolute square of the momentum operator matrix element for right-handed circularly polarized light which propagates along the helix axis, given by |T x +iT y | 2 . Notably, we observe a large anisotropy between the two halves of the first Brillouin zone, while the result for left-handed polarization is a mirror image to what we see in Fig. 6. Physically, this can be attributed to the conversion of the photon angular momenta to the translational motion of the free charge carriers projected onto the direction of the helix axis, with an unequal population of the excited subband in a preferential momentum direction controlled by the relative handedness of both the helix and the circular polarization of light. An intuitive mechanical analogue would be the rotary motion of Archimedes’ screw being converted into the linear motion of water along the direction of the screw axis dictated by the handedness of the thread. As such, our system of a double-gated nanohelix irradiated by circularly polarized light exhibits a photogalvanic effect, whereby one can choose the net direction of current by irradiating with either right- or left-handed circularly polarized light [44, 45, 89]. This differs from conventional one-dimensional superlattices, wherein the circular photogalvanic effect stems from the spin-orbit term appearing in the effective electron Hamiltonian and is consequently a weaker and hard-to-control phenomenon [90, 91]. The electric current induced by promoting electrons from the ground subband to an excited subband f via the absorption of circularly polarized light can be understood from the equation for the electric current contribution from the f th subband
$$ j_{f} =\frac{e}{2 \pi \rho} \int dq \left[ v_{f}(q) \tau_{f}(q) - v_{g}(q) \tau_{g} (q) \right] \Gamma_{CP}^{g \rightarrow f}(q), $$ (17)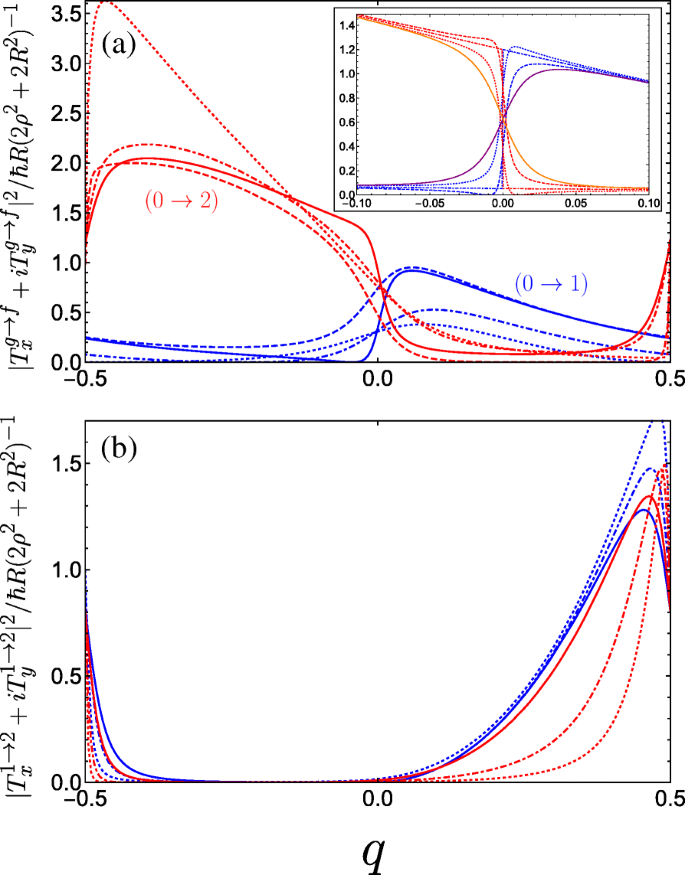
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by right-handed circularly polarized radiation |T x +iT y | 2 and for a variety of parameter combinations spanning the first incident of resonance. un The blue curves denote transitions between the ground and first band while the red curves denote transitions between the ground and second band, both with the following parameters:A g =0.5 and B g =0.3 for solid curves, A g =0.5 and B g =0.1 for dashed curves, A g =0.3 and B g =0.3 for dot-dashed curves, and A g =0.01 and B g =0.3 for dotted curves (as A g →0 the maximum of the 0→2 increases rapidly as it approaches q =− 1/2). The inset plots the behaviour as B g is tuned through resonance for A g =0.5; dotted is B g =0.24, dot-dashed is B g =0.25, and dashed is B g =0.26. The solid purple (orange) curve denotes transitions between the ground and first (second) band at resonance with C ⊥ =0.05 applied. b Plots transitions between the first and second bands. The different blue curves keep A g =0.5 fixed and vary B g =0, 0.2, and 0.3 corresponding to dotted, dot-dashed, and solid. The different red curves keep B g =0.3 fixed while varying A g =0.05, 0.1, and 0.3 as dotted, dot-dashed, and solid. We have omitted plots for C ⊥ ≠0 here as it yields no great qualitative change to the matrix elements
where \(v_{g,f}(q)=(\rho /\hbar)\partial \varepsilon _{g,f}/\partial q \) is the antisymmetric electron velocity v ( q )=− v (− q ) (which we can deduce from the symmetric dispersion curves), τ g,f ( q ) is a phenomenological relaxation time, and \(\Gamma _{CP}^{g \rightarrow f}(q)\) is the transition rate resulting from the optical perturbation of the electron system. Given that \(\Gamma _{CP}^{g \rightarrow f}(q) \propto |T_{x}^{g \rightarrow f} + i T_{y}^{g \rightarrow f}|^{2}\) for right-handed circularly polarized light where T x y T y are given by Eqs. 16a and 16b, respectively. The anisotropy present in Fig. 6a enters Eq. 17 to yield a non-zero photocurrent. This current flows in the opposite direction for left-handed polarization. Such a circular photogalvanic effect is also exhibited in chiral carbon nanotubes under circularly polarized irradiation [92, 93], although tunability predominantly stems from manipulating the nanotube physical parameters, which are hard to control. The double-gated nanohelix system offers superior versatility by fully controlling the landscape of the superlattice potential, which can be used to tailor the non-equilibrium asymmetric distribution function of photoexcited carriers (as shown in Fig. 6 for inter-subband transitions between the three lowest subbands).
On a side note, we expect that (as with chiral carbon nanotubes [93–95]) the application of a magnetic field along the nanohelix axis can take up the role played by circularly polarized radiation, whereby the current is induced by a magnetic-field-induced asymmetric energy dispersion—which in turn produces an anisotropic electron velocity distribution across the two halves of the Brillouin zone.
Conclusiones
In summary, we have shown that the system of a nanohelix between two aligned gates modelled as charged wires is a tunable binary superlattice. The band structure for this system exhibits a diverse behaviour, in particular revealing energy band crossings accessible via tuning the voltages on the gates. The application of an electric field normal to the plane defined by the gates and the helix axis introduces an additional parameter with which to open a band gap at these crossings. Engineering the band structure in situ with the externally induced superlattice potential along a nanohelix provides a clear advantage over conventional heterostructure superlattices with a DQW basis [96, 97]. Both systems can be used as high-responsivity photodetectors, wherein tailoring the band structure (to the so-called band-aligned basis [98–100]) can lead to a reduction in the accompanying dark current. Here control over the global depth of the quantum wells also permits versatility over the detection regime, which can lie within the THz range. We have also investigated the corresponding behaviour of electric dipole transitions between the lowest three subbands induced by both linearly and circularly polarized light, which additionally allows this system to be used for polarization sensitive detection. Finally, the ability to tune the system such that a degenerate excited state is optically accessible from the ground state, along with the inherent chirality present in the light-matter interactions, may make this a promising system for future quantum information processing applications [101]. It is hoped that with the advent of sophisticated nano-fabrication capabilities [102], fully controllable binary superlattice properties will be realized in a nanohelix and will undoubtedly contribute to novel optoelectronic applications.
Appendix
Touching energy bands at Brillouin zone boundary when A g =C ⊥ =0
Here, we show using matrix algebra that in the picture of a binary superlattice pairs of subbands touch at the Brillouin zone edges if A g =C ⊥ =0 and B g ≠0, as seen from the solid blue curves in Fig. 3a. Equation 5 is equivalent to the following N -by-N pentadiagonal matrix Hamiltonian with zeros on the leading sub- and superdiagonals:
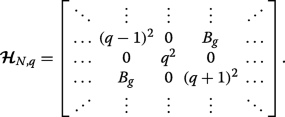 (18)
(18) Let us consider q =1/2 (we could alternatively take q =− 1/2) which makes the leading diagonal symmetric. We can then express this matrix Hamiltonian \(\widetilde {\mathcal {\boldsymbol {H}}}_{N} \equiv \boldsymbol {\mathcal {H}}_{N,q=1/2} \) in block form as
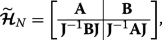 (19)
(19) donde
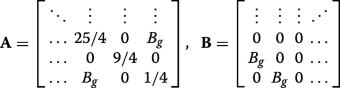 (20)
(20) are both of dimension N /2-by- N /2, and J is the exchange matrix. We may construct a matrix via permuting \(\boldsymbol {\mathcal {H}}_{N}\) with the N -by-N permutation matrix \(\boldsymbol {\mathcal {P}}_{N}\),
$$ \boldsymbol{\mathcal{P}}_{N} =\left[ \begin{array}{cccccc} 1 &0 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &\hdots &1 \\ 0 &1 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &1 &0 \\ \vdots &&&&&\vdots \\ 0 &\hdots &\hdots &1 &\hdots &0 \\ \end{array} \right], $$ (21)such that the permutation-similar matrix is
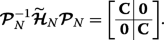 (22)
(22) Hence, the eigenvalues of \(\boldsymbol {\mathcal {P}}_{N}^{-1}\widetilde {\boldsymbol {\mathcal {H}}}_{N} \boldsymbol {\mathcal {P}}_{N}\), which are the same as the eigenvalues \(\widetilde {\boldsymbol {\mathcal {H}}}_{N}\), are double degenerate with the values given by the eigenvalue spectrum of the tridiagonal matrix C
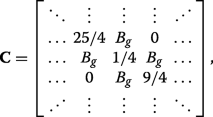 (23)
(23) which can also be expressed succinctly in terms of the previously defined matrices via \(\mathbf {C}=\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {A}\boldsymbol {\mathcal {P}}_{N/2}+\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {B}\mathbf {J}\boldsymbol {\mathcal {P}}_{N/2}^{4}\). We can see that applying C ⊥ ≠0 (inset of Fig. 3a) or both C ⊥ y A g ≠0 (inset of Fig. 3b) ruins the symmetry in the matrix Hamiltonian and prevents the existence of eigenvalues with multiplicity beyond unity, resulting in the appearance of band gaps.
Energy crossing at centre of Brillouin zone between third and forth subbands
As an example, let us specifically consider the case where p =2, wherein the matrices (12) and (13) become:
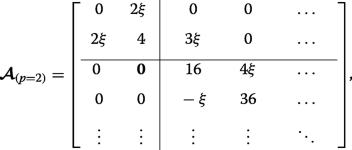 (24)
(24) and
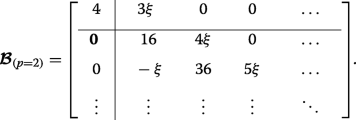 (25)
(25) This case corresponds to the crossings of the blue curves at the edge of the Brillouin zone in Fig. 3d (whereas p =0 results in crossings at q =0 in Fig. 3b). The lower eigenvalues are found exactly by diagonalizing each of the two finite matrices and they interlace, yielding \(\eta _{0,1,2} =2-\sqrt {4+4\xi ^{2}}, 4, 2+\sqrt {4+4\xi ^{2}}\). The infinite lower-right-hand block tridiagonal matrices coincide, thus the remaining double degenerate eigenvalues are found by approximately or numerically solving Det[D - η I ]=0.
Disponibilidad de datos y materiales
The data for the figures all stem from numerically diagonalizing the matrix described by Eq. 5 and can readily be achieved in any numerical software package. With this in mind, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Nanomateriales
- Contador binario de 3 bits
- Numeración decimal versus binaria
- Numeración octal y hexadecimal
- Suma binaria
- Números binarios negativos
- Resta binaria
- Desbordamiento binario
- Secuencia de recuento binario
- Un sumador binario
- Oxinitruro de boro y carbono como nuevo fotocatalizador sin metales
- Primeros pasos con Go on PLCnext



