Predicción y análisis eficientes del atrapamiento óptico a nanoescala mediante el método de interconexión y desgarro de elementos finitos

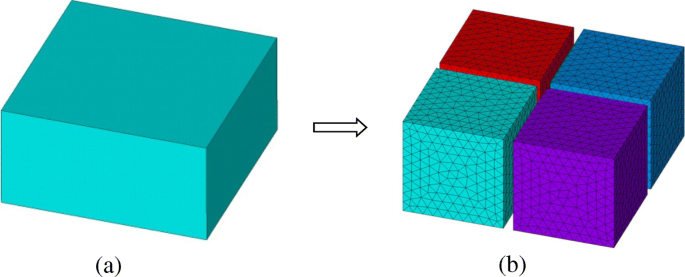
Un esquema de división de dominio con subdominios no superpuestos en el método FETI-DP. un Dominio original. b Subdominios divididos y mallas discretizadas

donde E ⁱ denota el campo eléctrico desconocido que se resolverá en \ ({\ Omega} ^ i \), k ₀ y η ₀ son el número de onda de espacio libre y la impedancia intrínseca, respectivamente, y \ ({\ mathbf {J}} _ i ^ {\ mathrm {imp}} \) es la corriente impresa. \ ({\ Gamma} _ {\ mathrm {ABC}} ^ i \) significa la condición de límite absorbente (ABC) para truncar la región abierta infinita. Cabe señalar que k ₀ debe reemplazarse por la impedancia de onda en el medio si el medio circundante no es de espacio libre, que es común para el atrapamiento óptico. En la interfaz del subdominio Γ ⁱ , se requiere una condición de límite asumida para generar un problema de valor de límite completo en Ω ⁱ . Aquí, una condición de transmisión tipo Robin con una variable auxiliar desconocida Λ _i se impone como

donde \ ({\ hat {n}} ^ i \) denota un vector exterior normal unitario en la interfaz del subdominio Γ ⁱ y α ⁱ es un parámetro complejo que a menudo se puede elegir como jk ₀ . A continuación, todos los subdominios se discretizan mediante elementos tetraédricos. En cada elemento, expandimos E con funciones de base vectorial N y coeficiente de campo eléctrico desconocido E como

donde s denota el número de funciones de base de vector en cada elemento tetraédrico. s se elige 6 para la función de base tradicional de orden inferior basada en el borde, mientras que es más grande para la función de base vectorial de orden superior, ya que se introducen funciones de base adicionales basadas en la cara o el volumen.

Aplicando el método de Galerkin, la ecuación de la matriz FEM en Ω ⁱ sobre el coeficiente de campo eléctrico desconocido E ⁱ se puede obtener como

donde las notaciones de subíndice c y r distinguir los grados de libertad de las esquinas (DOF) y los DOF ​​restantes, lo que extrae los DOF ​​de las esquinas como una variable primaria para construir el esquema dual-primal (DP). Aquí, K es la matriz del sistema FEM y f es el vector de excitación. B es una matriz booleana que extrae los DOF ​​de interfaz de un subdominio. λ es una variable dual generada al expandir Λ _i , que también se denomina multiplicador de Lagrange.

Luego, los subdominios adyacentes pueden interconectarse imponiendo el campo eléctrico tangencial y la continuidad del campo magnético en las interfaces. Ensamblamos todas las interfaces del subdominio y eliminamos todas las incógnitas internas del subdominio E ⁱ . Una ecuación de interfaz global reducida sobre la variable dual λ se puede obtener como

La ecuación (6) se puede resolver mediante métodos iterativos, como el método de residuo mínimo generalizado (GMRES). \ ({\ tilde {\ mathbf {K}}} _ {cc} \) es el sistema de esquina global, que puede acelerar la convergencia iterativa en el espacio primario. Se puede emplear un preacondicionador adecuado para mejorar la tasa de convergencia iterativa, como la descomposición LU aproximada inversa e incompleta. Una vez que la variable dual λ se resuelve, el campo eléctrico dentro de cada subdominio se puede evaluar de forma independiente mediante (5). Para la construcción de la matriz global \ ({\ tilde {\ mathbf {K}}} _ {rr} \), se necesita construir la función numérica de Green del subdominio \ ({\ mathbf {Z}} _ {rr} ^ i \) con una forma de

donde se incluye la inversa de la matriz FEM del subdominio \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \). Además, para matrices \ ({\ tilde {\ mathbf {K}}} _ {rc} \), \ ({\ tilde {\ mathbf {K}}} _ {cr} \) y \ ({\ tilde {\ mathbf {K}}} _ {cc} \) y los vectores \ ({\ tilde {f}} _ r \) y \ ({\ tilde {f}} _ c \), el \ ({\ left ({ \ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) debe calcularse. Las construcciones de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) en la etapa de preprocesamiento, así como sus productos de matriz-vector (MVP) en La etapa de solución iterativa es computacionalmente costosa. Aunque \ ({\ mathbf {K}} _ {rr} ^ i \) es escaso, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \ ) son densos, lo que significa altos costos computacionales. A continuación, se introduce un método de dispersión de rango bajo para acelerar el cálculo de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \). Dado que algunas submatrices en el sistema de interfaz global se pueden representar en forma de matriz de rango bajo, su cálculo se puede realizar con un algoritmo de rango bajo, lo que mejora el rendimiento del FETI-DP. Puede verse que el FETI-DP proporciona operaciones de subdominio independientes, de modo que puede aprovechar la computación en paralelo para mejorar la eficiencia. Para un esquema paralelo eficiente, un principio de división de dominio es hacer que el número de DOF en cada subdominio sea lo más equilibrado posible. Por lo tanto, el tamaño de los subdominios debe relacionarse con la densidad de discretización de la malla. Por lo general, los subdominios pequeños se adoptan en áreas de malla fina, mientras que los subdominios grandes se adoptan en áreas de malla gruesa.

Separación de rango bajo

Se propone un enfoque de dispersión de bajo rango para proporcionar una forma de escasez de datos para mejorar la eficiencia de FETI-DP. Aquí, data-sparse significa que estas matrices en realidad no son escasas, pero son escasas en el sentido de que ciertos subbloques de ellas se pueden representar mediante formas de matriz de descomposición de bajo rango como

donde X y Y están en formas de matriz completa, y el rango k es mucho más pequeño que m y n . La matriz \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) se puede representar mediante formas matriciales con datos dispersos, ya que posee la propiedad matricial de una integral operador. Por lo tanto, siempre que \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) posea una propiedad de rango bajo en un subdominio dado, se puede calcular y almacenar de manera eficiente en formularios con escasez de datos con el enfoque de dispersión de rango bajo, que acelera los MVP en la solución iterativa.

Los procesos del enfoque de dispersión de bajo rango se pueden dividir en los siguientes pasos:(1) construir un árbol de conglomerados subdividiendo el conjunto de funciones base en cada subdominio, (2) construir un árbol de conglomerados de bloques mediante la interacción de dos árboles de conglomerados, ( 3) genere una forma de datos dispersos de \ ({\ mathbf {K}} _ {rr} ^ i \) mediante una condición de admisibilidad, (4) realice algoritmos formateados de rango bajo para obtener la representación de datos dispersos de \ ( {\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \), y (5) ingrese la solución de los sistemas FETI-DP por algoritmo de datos dispersos. Puede emplearse un preacondicionador adecuado para acelerar la solución. Cabe señalar que la factorización LU con datos dispersos \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS} } \) se adopta para reemplazar la inversión de matriz \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \). Se emplea una técnica de disección anidada para mejorar aún más la eficacia de la esparsificación de bajo rango. La disección anidada usa separadores para producir grandes subbloques de cero fuera de la diagonal, que se mantendrán en cero durante la factorización LU para que pueda reducir significativamente los rellenos.

Para generar \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), primero construimos un árbol de clúster T _yo por subdivisión recursiva del conjunto de funciones de base basada en el borde del subdominio I ={1,2, …… N } usando un cuadro delimitador. Con la disección anidada, un grupo t dentro del cuadro delimitador correspondiente se divide en tres sucesores { s ₁ , s _sep , s ₂ }, donde s ₁ y s ₂ son los conjuntos de índices de los dos cuadros delimitadores desconectados y s _sep es el conjunto de índices del separador. La figura 2 a muestra un ejemplo sencillo de este proceso. Luego, un árbol de clúster de bloques T _{yo × Yo} se puede construir interactuando con dos árboles de clúster T _yo , como se muestra en la Fig. 2b, que se puede elegir como el árbol de clúster del conjunto de funciones de base basado en el borde original y el del conjunto de funciones de base de prueba en el método de Galerkin. A continuación, necesitamos introducir una condición de admisibilidad basada en la disección anidada para distinguir bloques completos, bloques de descomposición de bajo rango y bloques cero fuera de la diagonal en T _{yo × Yo} [23]. Por lo tanto, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) se puede producir llenando los bloques correspondientes con las entradas distintas de cero de \ ({\ mathbf {K}} _ {rr} ^ i \). Finalmente, la factorización LU con datos dispersos de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L }} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \ ) se puede calcular de forma recursiva desde

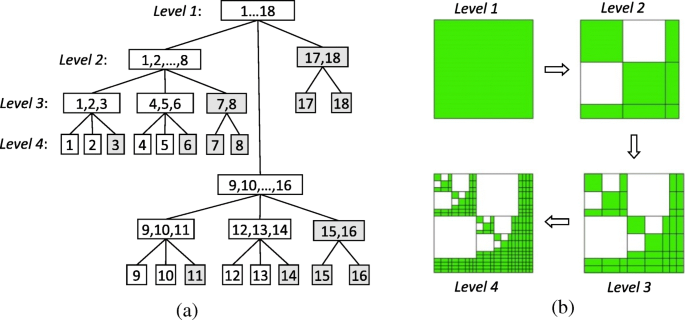
Construcciones de un árbol de conglomerados y un árbol de conglomerados de bloques de 4 niveles basados ​​en disección anidada. un Construcción de un árbol de conglomerados mediante la subdivisión recursiva del conjunto de funciones de base basada en el borde I ={1,2,… 18}. b Construcción de un árbol de racimo de bloques donde blanco los bloques son matrices cero y verdes los bloques pueden ser matrices completas o matrices de descomposición de bajo rango

donde la aritmética de matriz completa convencional se reemplaza por sus contrapartes de datos escasos [28]. Un error de truncamiento adaptativo ε _t se emplea para controlar la precisión de las aproximaciones de rango bajo. Los factores LU obtenidos \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) y \ ({\ left ({\ mathbf {U} } _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) se almacenan y se utilizan para construir \ ({\ mathbf {Z}} _ {rr} ^ i \) por

donde \ ({\ mathbf {B}} _ r ^ i {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \) y \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} {\ mathbf {B}} _ r ^ i \) puede ser calculado por un solucionador triangular superior e inferior con escasez de datos. El \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), \ ({\ left ({\ mathbf {U}} _ { rr} ^ i \ right)} _ {\ mathrm {DS}} \), y \ ({\ mathbf {Z}} _ {rr} ^ i \) ingresan el cálculo FETI-DP con datos dispersos hacia adelante y hacia atrás sustituciones (FBS) y MVP con pocos datos.

Fuerza óptica y potencial

Según la teoría de la electrodinámica, la fuerza óptica puede evaluarse mediante el tensor de tensión de Maxwell (MST) que revela la relación entre el campo electromagnético y el momento mecánico [29]. Una vez que se obtiene la distribución del campo electromagnético alrededor del objeto, la fuerza óptica se puede calcular integrando MST sobre una superficie cerrada que rodea al objeto. Basado en la distribución del campo eléctrico obtenida, el MST en cualquier coordenada puede ser construido por

donde el asterisco en superíndice denota el conjugado de campo eléctrico o campo magnético, ε son μ son la permitividad y la permeabilidad, y \ (\ overleftrightarrow {\ mathbf {I}} \) es una matriz identidad de 3 × 3. Por el producto externo de los vectores, la forma tensorial de \ (\ overleftrightarrow {\ mathbf {T}} \) se puede escribir como

donde el subíndice x , años , z denota los componentes en tres direcciones. Según la ampliación de E descrito en (4), las entradas de MST T _mn ( m , n = x , años , z ) se puede convertir en formas expandidas en el cálculo FETI-DP como

donde ω es la frecuencia angular; N y s han sido descritos en Eq. (4).

Finalmente, la fuerza óptica ejercida sobre el objeto se puede calcular integrando el MST sobre cualquier superficie cerrada que lo rodee por

Tenga en cuenta que el cálculo de la fuerza óptica también se puede implementar en paralelo, ya que la integral del MST se asigna a los subdominios correspondientes. Para un atrapamiento óptico estable, una de las condiciones principales es que la fuerza del gradiente sea mayor que la fuerza de dispersión. En otras palabras, la dirección de la fuerza total debe ser idéntica a la de la fuerza del gradiente, que siempre apunta a la posición donde la intensidad del campo eléctrico es más fuerte.

El potencial óptico es otro parámetro atractivo que revela la estabilidad del atrapamiento óptico. Según la fuerza óptica obtenida, la profundidad de potencial óptico U en la posición r ₀ puede ser calculado por

donde el subíndice ∞ denota infinito definido como el punto de referencia con potencial cero. El valor de U puede ser representado por k _B T, donde k _B denota la constante de Boltzmann de 1.3806488 × 10 ⁻²³ J / K y T es la temperatura ambiente. Generalmente, la partícula puede superar el movimiento browniano en solución y quedar atrapada de manera estable cuando U > 1 k _B T está satisfecho. De lo contrario, la partícula no puede quedar atrapada de forma estable. Dado que la fuerza óptica total incluye la componente de fuerza de gradiente conservadora y la componente de fuerza de dispersión no conservadora, la fuerza óptica total F de (15) no es conservador [30, 31]. Sin embargo, siempre que el movimiento de la nanopartícula esté restringido a una dimensión, esto arroja una definición inequívoca de un potencial óptico de (16), aunque la fuerza óptica total no es conservadora.

Resultados y discusión

Se presentan tres ejemplos para demostrar la eficacia del método propuesto. Dado que los metales nobles se utilizan comúnmente para excitar el plasmón superficial, seleccionamos materiales representativos de oro y plata para los análisis. El primer ejemplo calcula la fuerza óptica de una nanopartícula de plata para verificar la precisión del método propuesto. Los ejemplos segundo y tercero simulan y discuten el atrapamiento óptico de nanopartículas de oro. Para todos los ejemplos, el dominio infinito se trunca con ABC, y las distancias entre ABC y los objetos se establecen en una longitud de onda, lo que es suficiente para lograr una precisión aceptable. Todos los cálculos se realizan en una estación de trabajo Dell equipada con procesadores Intel Xeon de 3,6 GHz.

Nanocápsula plateada

Primero se considera un objeto de nanocápsula de plata para probar la precisión y eficiencia del método FETI-DP propuesto para predecir la fuerza óptica. La figura 3 ayb presenta su configuración y dimensiones. Los parámetros constitutivos de la plata son todos valores medidos tomados de [32]. Para implementar el esquema FETI-DP, primero se divide todo el dominio de análisis en 24 subdominios. Se requieren mallas más densas cerca de la superficie del metal para modelar el efecto de mejora del campo local plasmónico. Se adoptan elementos tetraédricos para la discretización, lo que conduce a un total de 6,9 ​​× 10 ⁵ incógnitas, incluidas 4,1 × 10 ⁴ incógnitas duales y 313 incógnitas de esquina. La luz incidente se ilumina en la dirección de + z , mientras que la dirección de polarización del campo eléctrico es - x .

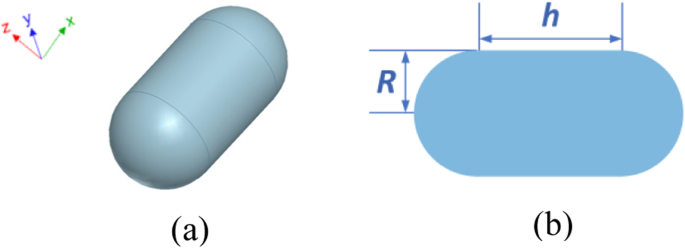
Configuración de una estructura de nanocápsulas de plata. un Vista 3D. b Vista frontal y dimensiones, donde R =30 nm y h =60 millas náuticas

Primero, cambiamos la longitud de onda de la luz incidente λ de 200 nm a 400 nm para simular las fuerzas ópticas ejercidas sobre la nanocápsula. Dado que el FETI-DP trabaja en el dominio de la frecuencia, las fuerzas ópticas se calculan en 15 puntos de frecuencia de muestreo. La Figura 4 muestra la curva calculada de fuerzas ópticas ejercidas sobre la nanocápsula de plata. Para indicar la precisión del FETI-DP, los resultados de la fuerza óptica del FETI-DP se comparan con los del software comercial Lumerical FDTD Solutions [33], y se puede observar una buena concordancia.

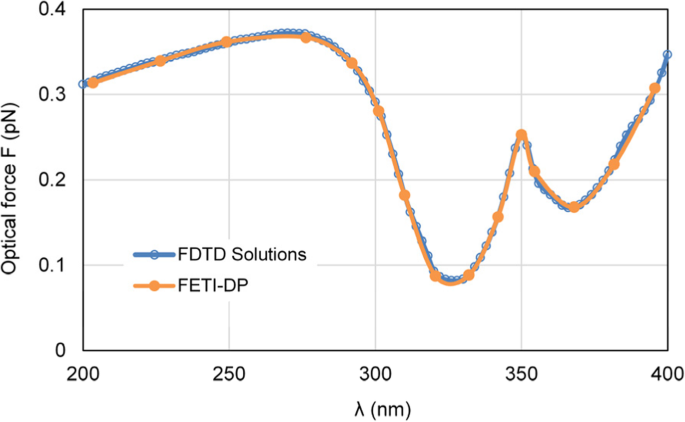
Resultados de las fuerzas ópticas ejercidas sobre la nanocápsula de plata, que varían con la longitud de onda λ of incident light, including the results of the FETI-DP and the commercial software FDTD solutions

Then, the performance of FETI-DP is tested for different numbers of subdomains. We increase the number of subdomains from 4 to 24 by keeping the discretization density. We assign each processor to deal with one subdomain. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF  = ‖OF _i  − OF _ref ‖/‖OF _ref ‖, where OF _i is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is a plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10 ⁶ unknowns, including 1.6 × 10 ⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. un 3D view. b Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by

$$ \mathrm{Speed}\ \mathrm{up}=\raisebox{1ex}{${T}_1$}\!\left/ \!\raisebox{-1ex}{${T}_{N_p}$}\right. $$ (17)

where \( {T}_{N_p} \) denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ  = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

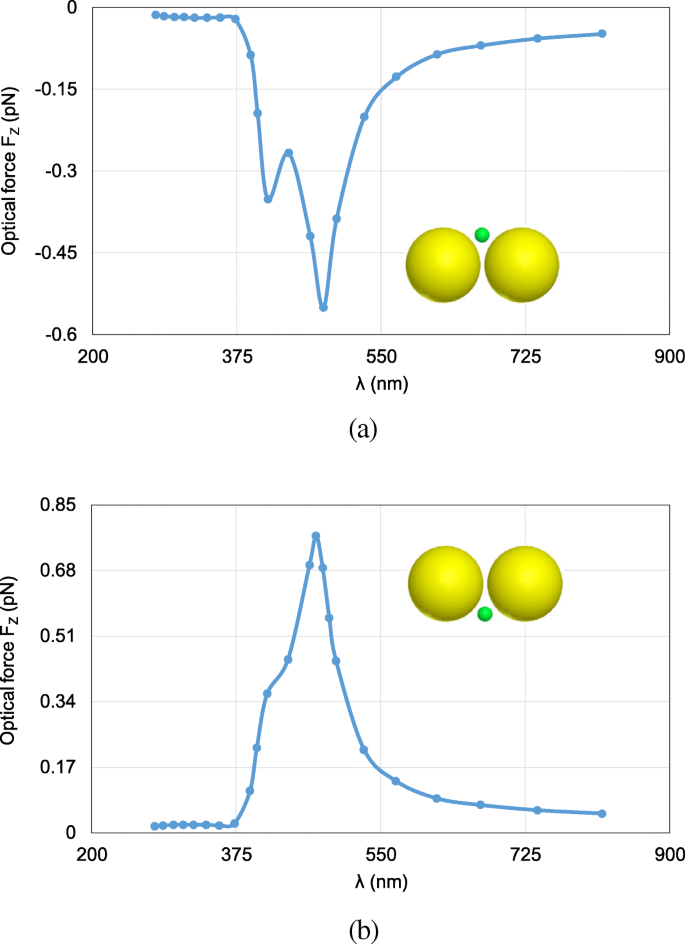
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. un The object nanosphere is located at (0, 0, 20 nm). b The object nanosphere is located at (0, 0, − 20 nm)

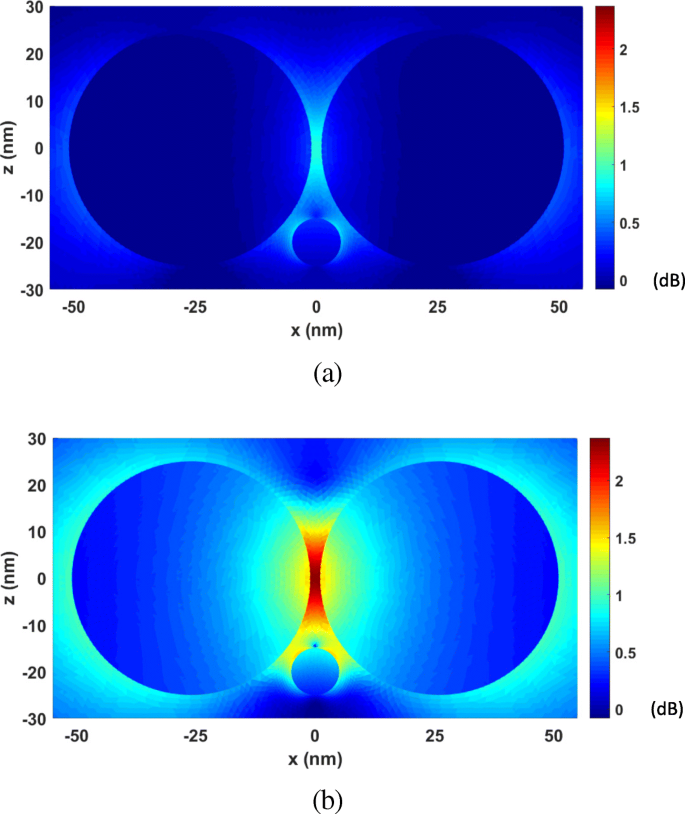
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. un λ = 300 nm (non-resonance wavelength). b λ  = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -eje. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -eje. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

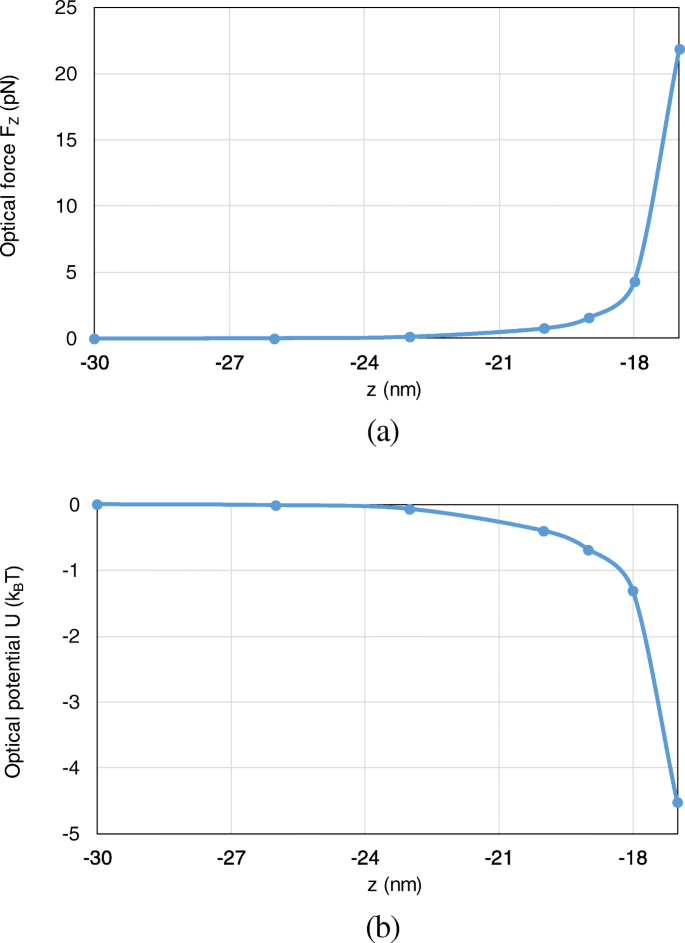
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). un The optical forces. b The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10 ⁻² , which is defined as |F ₁  − F ₀ |/|F ₀ |.

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r  = 2.25. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10 ⁶ unknowns, including 1.3 × 10 ⁵ dual unknowns and 1227 corner unknowns.

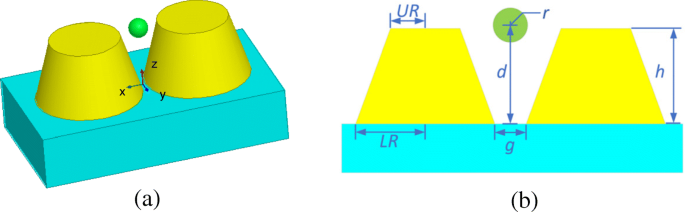
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. un 3D view. b Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ  = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

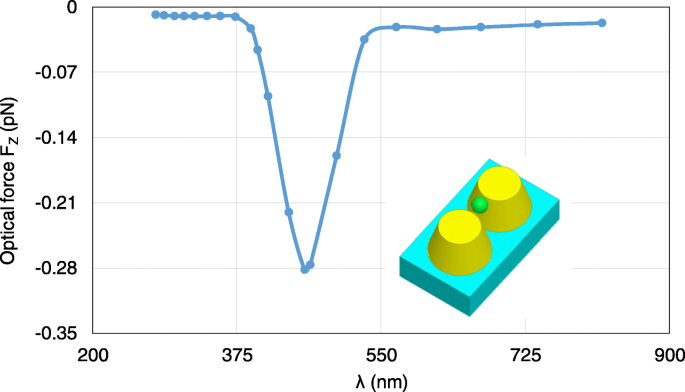
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

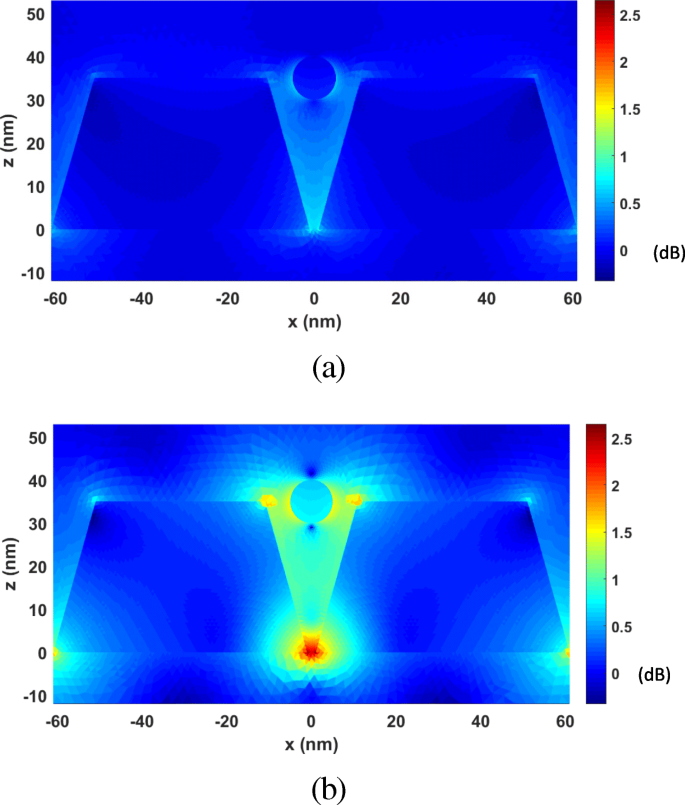
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. un λ =300 nm (non-resonance wavelength). b λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

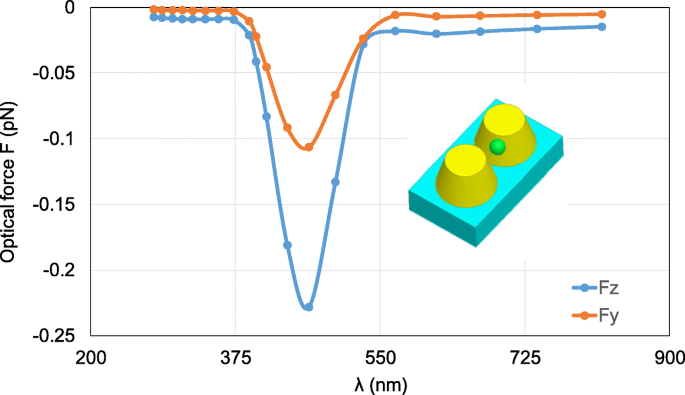
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -eje. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

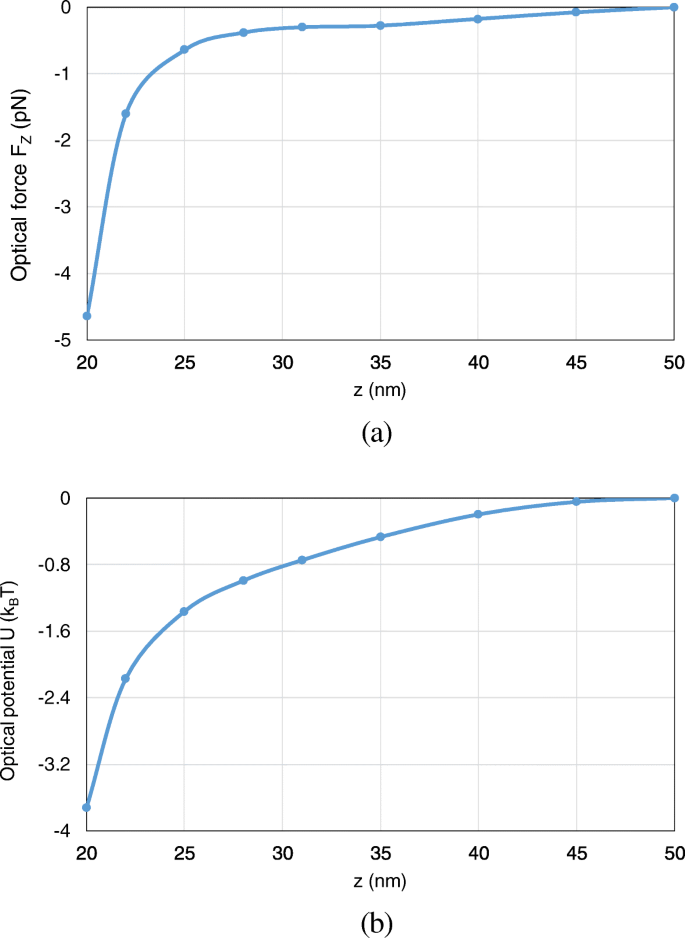
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). un The optical forces. b The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Conclusión

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Disponibilidad de datos y materiales

Todos los datos generados o analizados durante este estudio se incluyen en este artículo.

Abreviaturas

ABC:

Absorbing boundary condition

DOF:

Degrees of freedom

FDTD:

Dominio del tiempo de diferencia finita

FEM:

Método de elementos finitos

FETI-DP:

Dual-primal finite element tearing and interconnecting

MST:

Maxwell stress tensor

MVP:

Matrix-vector product

Relaciones matemáticas mágicas para nanoagrupaciones:erratas y apéndice Nanohélice de doble puerta como una nueva superrejilla binaria ajustable