Numeración decimal versus binaria

Vamos a contar de cero a veinte utilizando cuatro tipos diferentes de sistemas de numeración:marcas de almohadilla, números romanos, decimales y binarios:

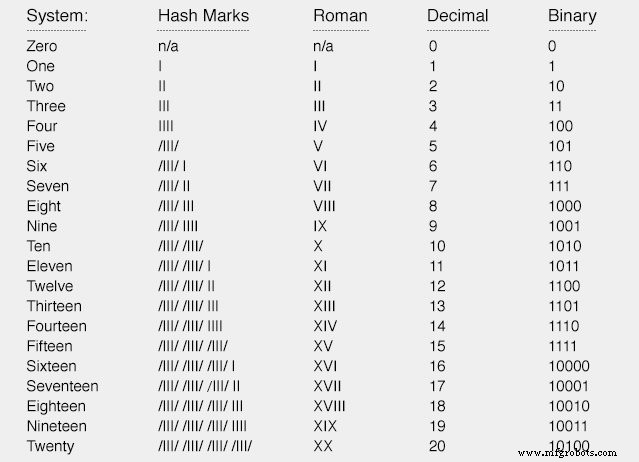
Ni las almohadillas ni el sistema romano son muy prácticos para simbolizar grandes números. Obviamente, los sistemas ponderados por lugar, como el decimal y el binario, son más eficientes para la tarea.

Sin embargo, observe cuánto más corta la notación decimal es la notación binaria, para el mismo número de cantidades. Lo que toma cinco bits en notación binaria solo toma dos dígitos en notación decimal.

Esto plantea una pregunta interesante con respecto a los diferentes sistemas de numeración:¿qué tan grande de un número se puede representar con un número limitado de posiciones o lugares de cifrado? Con el crudo sistema de marca de almohadilla, el número de lugares ES el número más grande que se puede representar, ya que se requiere un “lugar” de marca de almohadilla para cada paso entero.

Sin embargo, para los sistemas de numeración ponderados por lugar, la respuesta se encuentra tomando la base del sistema de numeración (10 para decimal, 2 para binario) y elevándolo a la potencia del número de lugares.

Por ejemplo, 5 dígitos en un sistema de numeración decimal pueden representar 100.000 valores de números enteros diferentes, de 0 a 99.999 (10 a la quinta potencia =100.000). 8 bits en un sistema de numeración binario pueden representar 256 valores de números enteros diferentes, de 0 a 11111111 (binario) o de 0 a 255 (decimal), porque 2 elevado a la octava potencia es igual a 256.

Con cada posición de lugar adicional al campo numérico, la capacidad para representar números aumenta en un factor de la base (10 para decimal, 2 para binario).

Una nota a pie de página interesante para este tema es una de las primeras computadoras digitales electrónicas, la Eniac.

Los diseñadores de Eniac optaron por representar números en forma decimal, digitalmente, utilizando una serie de circuitos llamados "contadores de anillo" en lugar de simplemente ir con el sistema de numeración binaria, en un esfuerzo por minimizar el número de circuitos necesarios para representar y calcular muy números grandes.

Este enfoque resultó ser contraproducente, y prácticamente todas las computadoras digitales desde entonces han tenido un diseño puramente binario.

Conversión de binario a decimal

Para convertir un número en numeración binaria a su equivalente en forma decimal, todo lo que tiene que hacer es calcular la suma de todos los productos de bits con sus respectivas constantes de peso posicional. Para ilustrar:

El bit en el extremo derecho se llama el bit menos significativo (LSB), porque se encuentra en el lugar del peso más bajo (el lugar del uno).

El bit en el extremo izquierdo se llama el bit más significativo (MSB), porque se encuentra en el lugar de mayor peso (el lugar de los ciento veintiocho).

Recuerde, un valor de bit de "1" significa que el peso de lugar respectivo se agrega al valor total, y un valor de bit de "0" significa que el peso de lugar respectivo no se suman al valor total. Con el ejemplo anterior, tenemos:

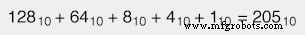
Si encontramos un número binario con un punto (.), Llamado "punto binario" en lugar de un punto decimal, seguimos el mismo procedimiento, dándonos cuenta de que cada lugar de ponderación a la derecha del punto es la mitad del valor del uno a la izquierda (del mismo modo que cada peso de lugar a la derecha de un decimal punto es una décima parte del peso del que está a su izquierda). Por ejemplo:

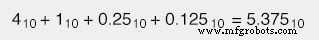
HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de matemáticas binarias