Un estudio de nanofibras de carbono y carbón activo como supercondensador simétrico en un electrolito acuoso:un estudio comparativo

Resumen

Los supercondensadores simétricos se fabrican con nanofibras de carbono (CNF) y carbón activado (AC) utilizando proporciones similares de aglutinante polimérico de fluoruro de polivinilideno (PVDF) al 7% en peso en un electrolito acuoso. En este estudio, se llevó a cabo una comparación de textura porosa y rendimiento electroquímico entre CNF y supercondensadores basados en CA. Los electrodos se ensamblaron en la celda sin un colector de corriente. Los electrodos preparados de CNFs y AC presentan una superficie Brunauer-Emmett-Teller (BET) de 83 y 1042 m ² / g, respectivamente. La estructura de poros dominante de los CNF es mesoporosa, mientras que la de AC es de microporos. Los resultados mostraron que la CA proporcionó una mayor retención de capacitancia específica hasta una velocidad de escaneo muy rápida de 500 mV / s. El carbono de CA tenía una capacitancia específica de 334 F / gy los CNF tenían 52 F / ga una velocidad de barrido de 5 mV / s en solución acuosa. Además, los resultados indican la conductividad superior de los CNF en contraste con sus contrapartes de CA. La resistencia en serie equivalente medida (ESR) mostró un valor muy pequeño para CNF (0.28 Ω) en comparación con CA que tiene una resistencia ESR de (3.72 Ω). Además, CNF entregó una potencia específica más alta (1860 W / kg) que la de CA (450 W / kg). Por otro lado, la CA proporcionó una energía específica más alta (18,1 Wh / kg) que la de los CNF (2 Wh / kg). Esto indica que la CA es buena para aplicaciones energéticas. Considerando que, CNF es bueno para aplicaciones de energía. De hecho, el área de superficie más alta conducirá a una mayor capacitancia específica y, por lo tanto, a una mayor densidad de energía para CA. Para CNF, una ESR más baja es responsable de tener una mayor densidad de potencia.

Tanto el supercondensador CNF como el AC exhiben una excelente estabilidad de carga y descarga de hasta 2500 ciclos.

Antecedentes

Los supercondensadores o condensadores electroquímicos han atraído mucho interés debido a su alta densidad de potencia y sus capacidades de ciclo largo. Han encontrado aplicaciones potenciales en vehículos eléctricos, dispositivos portátiles y herramientas eléctricas [1]. Los vehículos eléctricos necesitan alta potencia a una alta tasa de consumo de corriente, mientras que los sistemas de respaldo de memoria requieren una alta densidad de energía a una baja tasa de consumo de corriente. En consecuencia, el material debe elegirse de acuerdo con las aplicaciones deseadas [2]. Los componentes principales de un supercondensador son los electrodos y el electrolito. Dado que el almacenamiento de carga tiene lugar en la interfaz electrodo / electrolito, el área de la superficie del electrodo y el electrolito utilizado influirán en gran medida en el rendimiento del dispositivo. Las propiedades de los electrodos similares, la naturaleza del material, el grosor del electrodo, el área de la superficie, la distribución del tamaño de los poros y los grupos de superficies influyen en gran medida en el rendimiento del supercondensador [3]. Los materiales de carbono se utilizan ampliamente como electrodos debido a su bajo costo, la diversidad disponible de morfologías y la estabilidad química y térmica [4, 5, 6, 7]. La morfología tubular a nanoescala de CNF puede ofrecer una combinación única de baja resistividad eléctrica y alta porosidad en una estructura fácilmente accesible [8]. Un material de CA es un material muy atractivo para los supercondensadores debido a su alta porosidad, bajo costo, abundancia, alta estabilidad y ciclos de carga-descarga [9]. La fabricación de electrodos (AC o CNF) para supercondensadores requiere la adición de aglutinantes, por ejemplo, poli (tetrafluoroetileno) (PTFE), cloruro de polivinilideno (PVDC) y fluoruro de polivinilideno (PVDF), en proporciones que generalmente varían de 5 a 10% en peso. . % para mantener la integridad de los electrodos [10, 11]. Sin embargo, el aglutinante bloquea la parte de la porosidad del carbono y, además, provoca un aumento de la resistividad eléctrica [11,12,13].

La capacitancia del supercondensador está altamente relacionada con el material del electrodo y el electrolito. La compatibilidad del electrolito con el material del electrodo también juega un papel crucial en el desarrollo del supercondensador porque la doble capa eléctrica se construye en la interfaz electrodo / electrolito. El voltaje de un supercondensador depende de la ventana de potencial de estabilidad del electrolito. Los electrolitos acuosos suelen proporcionar potencial hasta 1,0 V y electrolito orgánico hasta 2,7 V [14]. Los electrolitos acuosos son ecológicos, mientras que los electrolitos orgánicos no son buenos para el medio ambiente. Los electrolitos acuosos se componen principalmente de pequeños aniones y catión hidratado simple (nivel de angstrom). Estos iones pueden penetrar fácilmente a los microporos, mesoporos y macroporos del material bajo el campo eléctrico aplicado. La doble capa eléctrica (EDL) construida en la región interfacial del electrodo / electrolito se puede tratar como un condensador con un condensador eléctrico de doble capa (EDLC), que se puede expresar como C = ϵA / d . Donde ϵ es la constante dieléctrica del electrolito, A es el área de la superficie accesible a los iones, y d es la distancia de los iones a la superficie de los poros del electrodo de carbono del orden de un angstrom. De acuerdo con la ecuación anterior, se pueden tomar dos enfoques para mejorar el almacenamiento de carga de EDLC de manera efectiva:aumentar el SSA y reducir la distancia entre los iones y la superficie del carbono mediante el desarrollo [15].

En este trabajo, el objetivo es proporcionar un análisis comparativo del supercondensador simétrico basado en AC y CNF utilizando una cantidad similar de aglutinante PVDF 7% en peso para ambos materiales.

Métodos / Experimental

Preparación de electrodos de CA y CNF

Se preparó un supercondensador simétrico basado en AC y CNF para su comparación. La referencia AC Carbopal CCP80 de Donau Carbon es suministrada por QuimicsDalmau. Los CNF tienen una estructura de copa apilada de grafito helicoidal, hay presencia de Ni (6%), el diámetro es de 20 a 80 nm, la longitud (MEB)> 30um y la resistividad eléctrica de 10 ⁻² Ω cm.

Se utilizó PVDF como aglutinante. Con el fin de comparar la preparación de electrodos para el análisis de supercondensadores para ambos materiales (AC, CNF) se logró de una manera similar siguiendo los pasos a continuación.

Paso 1:Molienda de (AC o CNF) en un molino planetario de bolas de circonio (Pulverisette 7 de Fritch) empleando una frecuencia de 500 rpm durante 30 min. Paso 2:Mezcla de AC o CNFs 93% en peso con 7% en peso de polímero PVDF usando 15 ml de acetona en un mortero de ágata. Etapa 3:La suspensión se mezcló luego usando un agitador mecánico durante 60 minutos seguido de un ultrasonido durante 30 minutos. Etapa 4:La suspensión de la mezcla se secó en un horno durante 60 min a 70 ° C. Paso 5:En el último paso, la suspensión seca se utilizó para preparar los electrodos, de una manera, utilizando una prensa hidráulica con un juego de matrices (10 mm) a 10 toneladas de fuerza. La masa calculada de los discos de electrodos preparados basada en CNF y AC fue 0.018 y 0.02 g, respectivamente.

Caracterización de superficies

La textura porosa y el área de superficie específica y la distribución del tamaño de los poros de los electrodos CNF y AC se obtuvieron por adsorción física de gases N ₂ a 77 K usando Micromeritics TriStar 3000 V6.04 A. Todas las muestras se desgasificaron a 100 ° C durante 4 h antes de las mediciones de adsorción. La superficie específica ( S _APUESTA , m ² / g) se determinó mediante el método multipunto de Brunauer-Emmett-Teller (BET) en la región de la isoterma, que está limitada por el rango de presión relativa P / P ₀ =0,02-0,2. El volumen total de poros ( V _total , cm ³ / g) se calculó por el número de nitrógeno adsorbido en P / P ₀ ≈ 0,9932. El volumen de microporos y los valores de las áreas superficiales de micro ( S _micro , m ² / g) se investigaron utilizando el método t-plot (Harkins y Jura); la distribución del tamaño de los poros para la muestra de CNF se calcula a partir de las isotermas de adsorción mediante el método de Barrett-Joyner-Halenda (BJH); y el método MP se utiliza para calcular la distribución del tamaño de los poros para AC.

Caracterización morfológica

Las muestras de AC y CNF se examinaron mediante microscopía electrónica de barrido (SEM). Los análisis de TEM se realizaron en un sistema Philips Tecnai G2 F20 operado a 300 kV. Las muestras se suspendieron en etanol y se dispersaron ultrasónicamente durante 15 min. Se depositó una gota de la suspensión sobre una rejilla de cobre recubierta de carbono.

Caracterización electroquímica

La comparación del rendimiento electroquímico de CA y CNF como condensadores simétricos se estudió en celdas Swagelok de dos electrodos y utilizando un potenciostato Gamry 600 utilizando una solución de KOH 6-M como electrolito. La capacitancia específica de los materiales de los electrodos se investigó mediante voltamperometría cíclica (CV), carga / descarga galvanostática (GCD) y espectroscopia de impedancia electroquímica (EIS).

Resultados y discusión

Caracterización morfológica

La morfología de la superficie de los electrodos preparados se investigó mediante SEM Fig. 1 y TEM Fig. 1 (recuadro). Puede verse claramente que el aglutinante de PVDF une eficazmente los CNF de la figura 1a y la figura AC 1b. Las diferentes estructuras para ambos electrodos de CNF y AC son visibles. La estructura típica de CNF, la forma cilíndrica y la estructura de los cristales se insertan en la Fig. 1a. La imagen TEM de AC muestra esferas interconectadas con un tamaño homogéneo y una superficie más suave insertada en la Fig. 1b.

Imágenes SEM e imágenes TEM (recuadro) para a CNF y b AC

Textura de poros de CNF y AC

El N ₂ La isoterma de adsorción / desorción de CNF y AC se muestra en la Fig. 2. Las distribuciones de volumen y tamaño de poro se calcularon mediante el método BJH, el método del gráfico t y el método MP. Sólo el análisis del método MP puede revelar la fina diferencia de distribución del tamaño de los microporos de la muestra [16]. La distribución del tamaño de los poros de los materiales se clasifica en tres grupos:microporos (<2 nm), mesoporos (2-50 nm) y macroporos (> 50 nm) [17]. La isoterma de los CNF presenta un pequeño bucle de histéresis desde el rango de presión superior al medio, lo que indica que los CNF contienen una estructura mesoporosa. Debido a eso, solo se usa el método BJH para la detección del tamaño de poro, ya que el método MP no puede detectar meso y macroporosidad. Según la clasificación de la IUPAC, la isoterma de los CNF se puede clasificar como isoterma de tipo II. La distribución de poros de los CNF es la siguiente:59% de mesoporos (2 a 50 nm), 17,9% de microporos (0,5 a 2 nm) y 23% de macroporos (> 50 nm). Los detalles se presentan en la Tabla 1.

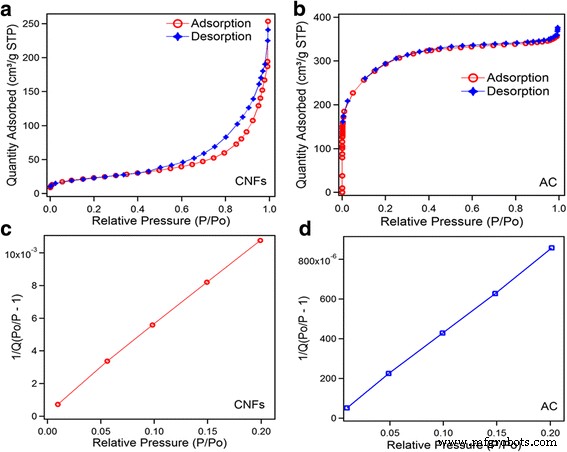
Isotermas de adsorción / desorción de nitrógeno, a CNF y b C.A. APUESTA superficie c CNFS y d AC

La isoterma de adsorción / desorción de CA presenta que la mayor parte de la cantidad de adsorción tiene lugar a una presión relativa muy baja ( P / P ₀ ≤ 0,02) y una meseta de presión relativa baja a alta (0,6-0,8). El volumen total de poros es de 0,582 cm ³ / ga presión relativa ( P / P ₀ =0,9932). La Figura 2b presenta que la curvatura de la isoterma de 0 a 0,4 de presión relativa presenta un volumen de poro para poros de menos de 50 nm (micro + meso), y este volumen de poro es igual a 0,534 cm ³ / g, que es la indicación de una estructura muy microporosa. El sistema de isoterma de muestra de CA se clasifica como isoterma de tipo I. La distribución de poros de AC es la siguiente:supermicroporos (0,5 a 2 nm) ocuparon el 33%, ultramicro (0,2 a 0,5 nm) ocuparon el 55% y los mesoporos ocuparon el 12%. El método MP se utilizó para la detección del tamaño de poro de CA porque el método BJH no puede detectar la microporosidad de CA. Los detalles se presentan en la Tabla 1.

El área de superficie específica (BET) se determinó mediante el método de Brunauer-Emmett-Teller (BET) de múltiples puntos en la región de la isoterma, que está limitada por el rango de presión relativa P / P ₀ =0.02-0.2 como se ve en la figura 2c, d. El volumen total de poros (V _total , cm ² / g) se calculó por el número de nitrógeno adsorbido en P / P ₀ ≈ 0,9932. El volumen de adsorción muestra que las áreas de superficie BET para CNF y AC son 83 y 1042 m ² / g, respectivamente.

Los análisis de distribución del tamaño de los poros se presentan en la Fig. 3a, b obtenidos mediante el método MP para AC y utilizando el método Barrett-Joiner-Halenda (BJH) para CNF. Los CNF contienen dos tipos de poros dominantes centrados en los rangos de 3,36 y 7,1 nm, mientras que los AC se componen principalmente de poros de 0,47 nm. Las microesporas son beneficiosas para la acumulación de carga en los electrolitos acuosos [18, 19]. Se puede ver que para los CNF, la mayoría de los poros dominantes son mesoporos, mientras que para los ultramicroporos AC.

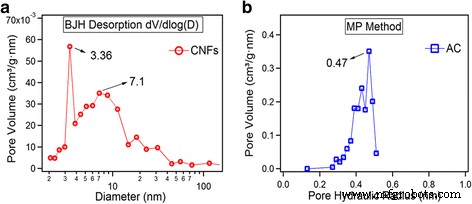
Distribución del tamaño de los poros. un CNF por método BJH. b AC por método MP

Comportamiento electroquímico de CNF y AC

Los principales enfoques aceptados para evaluar la capacitancia del supercondensador son la voltamperometría cíclica, la carga / descarga galvanostática y la espectroscopia de impedancia. El principio de funcionamiento de cada técnica varía de una a otra. El comportamiento electroquímico de CA y CNF se caracterizó por primera vez mediante voltamperometría cíclica en el rango de 0 a 1 V. CV es el método más conveniente para caracterizar el comportamiento capacitivo de los materiales de los electrodos. La capacitancia específica por unidad de masa para un electrodo se calculó usando las Ecs. (1, 2).

$$ {C} _ {\ mathrm {s}} =4 \ veces C / m $$ (1) $$ C =\ frac {q _ {\ mathrm {a}} + \ left | {q} _ {\ mathrm {c}} \ right |} {\ Delta V} $$ (2)

Donde C _s es la capacitancia específica en F / g, C es la capacitancia medida para la celda de dos electrodos por Eq. 2 y m es la masa total del material activo en ambos electrodos [20].

La Figura 4a, b muestra los CV de CNF y AC, respectivamente, con velocidades de exploración de 5 a 500 mV / s. Los CV de los CNF en una amplia gama de velocidades de escaneo tienen una forma cercana a la de una caja sin ninguna joroba, o la desviación indica características claras de doble capa y alta reversibilidad. Los CV para CA muestran una corriente mucho más alta que los CNF. A velocidades de escaneo bajas, la forma de CV es rectangular, lo que presenta que la respuesta del electrodo en la carga y descarga es altamente reversible. Sin embargo, a velocidades de escaneo más altas, CV se desvía de una forma rectangular. Podría haber varias razones posibles relacionadas con esta desviación, (1) debido a la baja conductividad eléctrica de la estructura porosa de CA de los poros internos que no son accesibles a los iones y (2) constante de tiempo distinta de cero y corriente transitoria elevada, lo que da como resultado un capacitor más largo tiempo de carga y colapso de la forma rectangular [21, 22].

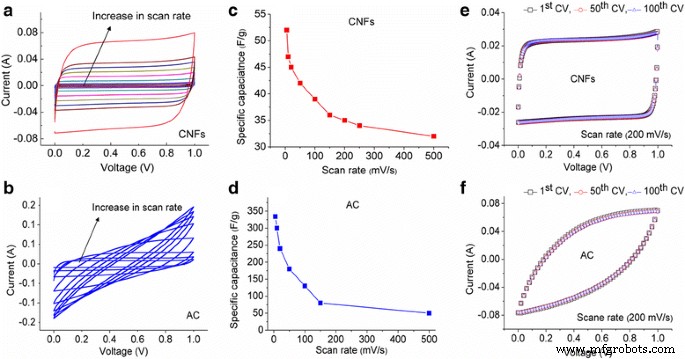
un , b CV de CNF y AC, respectivamente, a velocidades de exploración de 5, 10, 20, 50, 100, 150 y 500 mV / s; c , d comparación de capacitancia específica a diferentes velocidades de exploración; e , f CV de CNF y AC, respectivamente, del 1 ° al 100 ° ciclo

La Figura 4c, d presenta la comparación de capacitancia específica de CNF y CA de velocidades de exploración de 5 a 500 mV / s. Como se puede ver en la Fig. 4c, los CNF muestran la capacitancia específica más alta de 52 F / ga una tasa de exploración de 5 mV / s. La capacitancia específica disminuyó a 32 F / ga una velocidad de escaneo de 500 mV / s. Estos resultados indican una disminución moderada en la capacitancia específica y, a velocidades de exploración aún más altas, la mayor parte del área de superficie y los poros de los CNF son accesibles a los iones. La capacitancia de CA disminuye de 334 a 50 F / g durante 5 a 500 mV / s Fig. 4d. La capacitancia específica muy alta a una velocidad de exploración baja se debe a que los iones tienen tiempo suficiente para penetrar profundamente en la estructura microporosa (menos de 2 nm) de CA. Se puede suponer que a velocidades de barrido más altas, la mayor parte de los mesoporos de poros más grandes (2–50 nm) contribuyen a la capacitancia. Esto se debe principalmente a la diferencia en la velocidad de difusión del electrolito en los poros de diferente tamaño y también a la conexión de red entre los poros grandes y pequeños [23]. Como discutieron A.G. Pandolofo et al., El área de la superficie medida es aportada por todos los poros abiertos, pero no todos los poros son accesibles electroquímicamente [8].

La mayor capacitancia específica de CA en comparación con los CNF podría deberse a la mayor área de superficie, lo que da como resultado el aumento de las áreas accesibles para los iones de electrolito para el almacenamiento de carga dentro de poros relativamente pequeños.

Las curvas CV de los CNF y AC (Fig. 4e, f) indican un comportamiento de capacitancia estable medido hasta el ciclo 100 a una velocidad de barrido de 200 mV / s. El ciclo 100 de CV para ambas muestras conserva la forma que tenía para el primer ciclo, lo que sugiere una excelente estabilidad y procesos de electrodos reversibles.

El rendimiento supercapacitivo de CNF y AC fue comparado adicionalmente por GCD como se muestra en la Fig. 5a, b. La capacidad de descarga ( C ) se estima a partir de la pendiente ( dV / dt ) de la porción lineal de la curva de descarga usando la Ec. 3.

$$ {C} _ {\ mathrm {s}} =\ left (\ frac {2I} {\ left (dV / dt \ right) .m} \ right) $$ (3)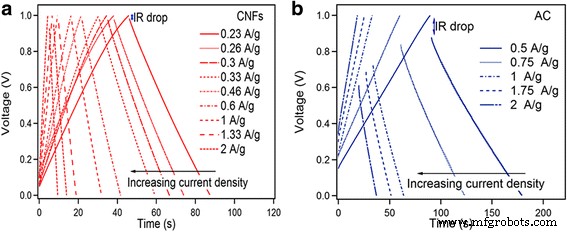

un Curvas de GCD a diferentes densidades de corriente de CNF. b Curvas GCD a diferentes densidades de corriente de CA

Donde C _s es la capacitancia específica en F / g, ∆V es la diferencia de voltaje durante la curva de descarga en V , yo es la corriente en A y ∆t es el tiempo de descarga en s .

Puede verse que los procesos de carga y descarga son casi simétricos, lo que indica una excelente reversibilidad electroquímica de los electrodos. Las curvas de descarga de CNF muestran un pequeño IR caída que implica una pequeña resistencia en serie equivalente, que es esencial para la característica de potencia de los supercondensadores. El IR inferior La caída de CNF al AC se debe a la alta conductividad de los CNF. El gran IR caída para CA significa mayor resistencia en serie equivalente (ESR). La capacitancia específica calculada para CNFs 23.8 F / ga 0.23 A / g disminuye a 19 F / ga 2 A / g. La capacitancia específica de CA disminuye de 159 F / ga una densidad de corriente de 0.5 A / ga 139 F / ga 2.5 A / g Fig. 6a. La capacitancia específica de ambos capacitores simétricos de CNF y CA disminuye con el aumento de la densidad de corriente, que es muy común para los supercondensadores y se debe principalmente a la limitación de difusión de los iones electrolíticos en las microesporas del electrodo.

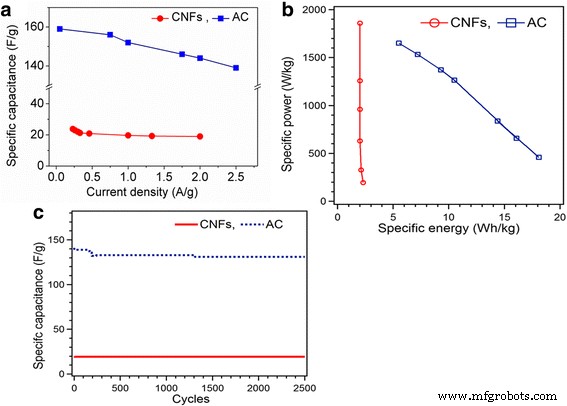
un Comparación de capacitancia específica de la curva de descarga de GCD. b Gráfico de Ragone de potencia específica contra energía específica para CNF y AC. c Estabilidad cíclica de CNF y AC

El poder específico, P , y la energía específica, E, entregada en el momento de la descarga se estimaron mediante las Ecs. (4) y (5).

$$ P =\ raisebox {1ex} {$ Vi $} \! \ Left / \! \ Raisebox {-1ex} {$ m $} \ right. $$ (4) $$ E =\ raisebox {1ex} {$ Vit $} \! \ Left / \! \ Raisebox {-1ex} {$ m $} \ right. $$ (5)

Donde V es el voltaje excluyendo IR soltar, i es la corriente de descarga y t es el momento [24].

Como se puede ver en la gráfica de Ragone Fig.6b, el electrodo CNF muestra una energía específica máxima de 2.3 Wh / kg a una potencia específica de 197 W / kg y una densidad de potencia máxima de 1860 W / kg a una energía específica de 2 Wh / kg indicando sus buenas características de potencia. Estos resultados muestran un aumento de potencia específica; la energía específica solo disminuye un poco, lo que es una firma de excelentes propiedades electroquímicas de alta densidad de energía y salida de potencia, por lo que es muy prometedora para su aplicación en escenarios donde se requiere una alta potencia de salida y una gran capacidad energética [25]. Para CA con el aumento en la potencia específica de 459 a 1650 W / kg, la energía específica disminuyó de 18,1 a 5,5 Wh / kg.

La estabilidad del ciclo también es un factor vital para aplicaciones prácticas. La medición del ciclo de carga-descarga galvanostática se realizó a una densidad de corriente constante de 2 A / g para CA y para CNF hasta 2500 ciclos. Fig. 6c. El comportamiento de CA durante el ciclo de estabilidad muestra una pequeña disminución en la capacitancia de 141 a 131 F / g en 2500 ciclos. Este resultado expresa que el desvanecimiento de la capacitancia se debe a las reacciones irreversibles al comienzo del ciclo [10]. Las mediciones de ciclos de CNF revelan una excelente retención de capacitancia de 19 F / g en 2500 ciclos.

El supercondensador se analizó adicionalmente mediante espectroscopia de impedancia electroquímica (EIS). Representa el gráfico de Nyquist en el rango de frecuencia de 10 kHz a 0,1 Hz para CNF y CA (Fig. 7a). Los gráficos de Nyquist consisten en (1) una intersección de alta frecuencia en el eje Z 'real, (2) un semicírculo en la región de frecuencia alta a media y (3) una línea recta en la frecuencia muy baja región [26]. En la región de alta frecuencia, las intersecciones con Z 'de CNF y AC son 0,11 y 0,16 Ω, respectivamente. Este valor se considera como la resistencia eléctrica total del material del electrodo, el electrolito y los contactos eléctricos [27]. El semicírculo de frecuencia alta a media corresponde a una combinación paralela de resistencia de transferencia de carga ( R _ct ) y capacitancia de doble capa [28]. Se puede ver que el semicírculo ( R _ct ) es mayor para CA (3,56 Ω) que para CNF (0,17 Ω). Las ESR calculadas fueron 0,28 y 3,72 Ω para CNF y AC, respectivamente. El valor muy pequeño de ESR para CNF, en relación con AC, indica el transporte / difusión fácil de electrones e iones en los electrodos de CNF. Esto indica que el electrodo CNF tiene una conductividad mucho mayor que el electrodo AC. Como también se observa en la Fig. 7a, las CNF mostraron una pendiente más alta de la línea recta, en el rango de baja frecuencia, que la CA. Esto significa que los CNF exhiben un comportamiento capacitivo más alto que los AC.

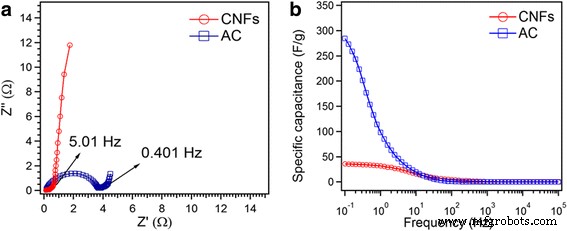
un Gráfico de Nyquist de CNF y AC. b Comparación de Csp calculada a partir de EIS.

La capacitancia específica, C _s , del supercondensador CNF y AC también se calculó a partir del análisis de impedancia empleando el componente imaginario de la impedancia mediante la siguiente ecuación [29].

$$ {C} _ {\ mathrm {s}} =4 \ left (- \ left (1/2 \ pi f {z} ^ {\ prime \ prime} m \ right) \ right) $$ (6)

Donde f es la frecuencia en Hz, z ”Es el componente imaginario de la impedancia, y m es la masa de CNF o AC calculada para un electrodo. La Figura 7b muestra el cambio más alto en la capacitancia específica de CNF y CA por debajo de la frecuencia de 10 Hz. La capacitancia específica obtenida para CNF (36 F / g) y CA (284 F / g) a la frecuencia de 0.1 Hz es bastante comparable a la capacitancia calculada por CV. De hecho, una mayor capacitancia específica para CA se debe a una mayor superficie disponible para la acumulación de carga en la interfaz sólido-líquido.

Constante de tiempo τ es la propiedad del supercondensador que refleja la respuesta del dispositivo. Un pequeño valor de τ da indicios de una mejor respuesta. La constante de tiempo τ se calculó utilizando la siguiente ecuación:

$$ 2 \ tau =\ frac {E _ {\ mathrm {D}}} {P _ {\ mathrm {D}}} $$ (7)

Donde E _D es la densidad de energía y P _D es la densidad de potencia. E _D y P _D se calcularon utilizando las siguientes ecuaciones:

$$ {E} _ {\ mathrm {D}} =0.5C {V} ^ 2 / m $$ (8) $$ {P} _ {\ mathrm {D}} ={V} ^ 2/4 \ izquierda (\ mathrm {ESR} \ derecha) m $$ (9)

Donde V es la ventana de voltaje durante la curva de descarga de carga, C es la capacitancia de la carga-descarga y la ESR calculada a partir de la espectroscopia de impedancia, y m es la masa del electrodo. La constante de tiempo calculada τ para CA fue de 3,1 sy para CNF fue de 0,08 sa una densidad de corriente de 2 A / g, lo que indica una mejor respuesta capacitiva para los CNF.

La relación entre Z _real y la frecuencia nos da información sobre el electrolito y la resistencia de transferencia de carga en el electrolito Fig. 8a. El comportamiento de resistencia del electrodo está muy influenciado por la naturaleza del electrodo de carbono. Tanto para CNF como para CA a alta frecuencia de 100 KHz, la ESR se encuentra en sus valores más bajos en el orden de aproximadamente 0,1 Ω, que presenta la resistencia del electrolito R s. Al bajar la frecuencia, hasta 506 Hz, hay un fuerte aumento en la resistencia de CA en relación con los CNF. A la frecuencia más baja observada (0,1 Hz), se observó que la ESR tenía un valor de 1,87 y 4,5 Ω para CA y CNF, respectivamente. El aumento de la VSG con la frecuencia decreciente podría deberse a la dificultad de penetración de la señal eléctrica en los poros más profundos (llenos de electrolito) y / o en las partículas más pequeñas [30]. Esta variación puede justificarse por el hecho de que a medida que disminuye la frecuencia, los iones pueden alcanzar fácilmente las zonas más profundas de los poros del carbón activado y, en consecuencia, su desplazamiento más prolongado dentro del electrolito da como resultado una mayor resistencia del electrolito [31].

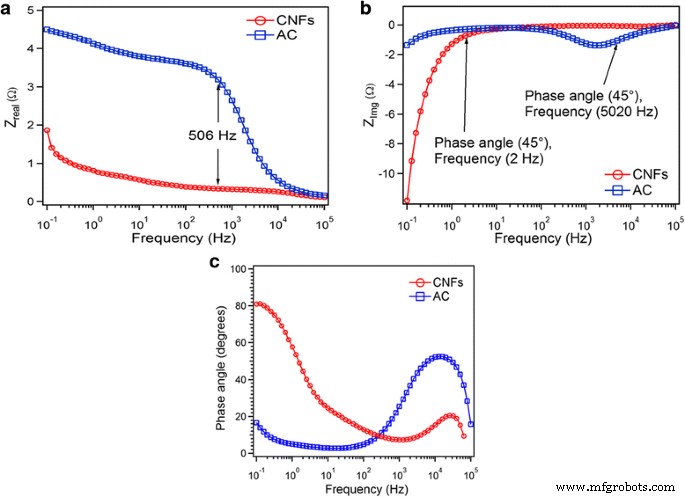
un Lo real y b las partes imaginarias se trazan en función del logaritmo de la frecuencia y c cambio de fase en función de la frecuencia para CA y CNF

La relación entre Z _Img y la frecuencia nos da información sobre el tiempo de relajación ( τ ₀ ) en la región límite, donde el supercondensador se transfiere del resistor al condensador Fig. 8b. La constante de tiempo τ ₀ que corresponde al ángulo de fase de 45 ° representa la transición del condensador electroquímico de un comportamiento puramente resistivo a puramente capacitivo. Es bien sabido que una mayor entrega de energía corresponde a una menor τ ₀ valores. Para frecuencia, f> 1 / τ ₀ , actúa como una resistencia pura, y para f <1 / τ ₀ , se comporta como un condensador puro. El ángulo de fase de 45 ° se encontró para CA a una frecuencia de 5020 Hz y para CNF a 1,99 Hz. Esto muestra que el tiempo de relajación para la CA es mucho menor que el de los CNF. Por lo tanto, la traducción del comportamiento resistivo al comportamiento capacitivo para CA es mucho más rápida que los CNF.

La Figura 8c representa la variación del ángulo de fase en función de la frecuencia, lo que se conoce como diagrama de Bode. Se encuentra que los ángulos de fase son - 20 ° y - 88 ° a baja frecuencia de 0.1 Hz en los sistemas AC y CNF, respectivamente (Fig. 8c). En general, la aproximación del ángulo de fase a - 90 ° confirma un mejor rendimiento capacitivo y un rápido proceso de carga y descarga. La constante de tiempo de relajación, τ 0, define el tiempo requerido para entregar la carga almacenada de manera efectiva como se ve en la Fig. 8b [32].

Efecto de la estructura de carbono y la textura porosa en el rendimiento de EDLC

A partir de la caracterización electroquímica, es evidente que el supercondensador basado en electrodos de CA proporciona una capacitancia específica más alta que los CNF en el electrolito KOH 6-M. Según la ecuación, ∁ =∈ A / d , distancia ( d ) es muy pequeño cuando el electrodo contiene microporos. La mayor capacitancia de la CA se debe a algunas propiedades importantes, tales como un área de superficie BET más alta y la existencia de un 88% más alto de ultramicroporos y microporos. Considerando que, las muestras de CNF tienen una superficie BET baja y un 17,9% de microporos. Otro factor importante que influye en la capacitancia está relacionado con la siguiente ecuación, τ = L ² / D . Donde L se refiere a la longitud de transporte de iones y D se refiere al coeficiente de transporte de iones. Según esta ecuación, los iones entran rápidamente dentro de los microporos, pero a medida que aumenta el tamaño de los poros, también aumenta el área externa. Debido a este hecho, los iones se acumulan fuera de los poros, lo que da como resultado una disminución de la capacitancia. Según E. Raymundo-Pinero et al., En solución acuosa, la formación de doble capa es mucho más favorable cuando el tamaño de los poros es de alrededor de 0,7 nm [19]. Nuestros resultados revelan que el tamaño de los poros de CA (0,47 nm) está en el rango óptimo para construir la doble capa, por lo que presenta una mayor capacitancia específica que los CNF.

Conclusiones

Los electrodos CNF y AC se prepararon con una técnica similar y se compararon como supercondensadores simétricos utilizando una solución acuosa. Se encontró que la distribución del tamaño de los poros, el área de la superficie del electrodo y la resistencia total del electrodo juegan un papel crucial en la determinación del rendimiento del supercondensador. Los resultados de BET revelan que AC tiene una gran cantidad de microporos y una estructura de ultramicroporos que da una superficie de 1042 m ² / g, mientras que el electrodo CNF contiene una estructura mesosporosa dominante y una superficie de 83 m ² /gramo. Debido a eso, el material de CA ofrece una capacitancia específica (334 F / g) mucho más alta que los CNF (52 F / g). De hecho, una capacitancia específica más alta para CA dio una energía específica más alta (18,1 Wh / kg) que la de los CNF (2 Wh / kg). Por otro lado, los CNF revelan una ESR más baja (0,28 Ω) que la CA (3,72 Ω). Las potencias específicas obtenidas en función del valor de ESR fueron 1860 y 450 W / kg para CNF y AC, respectivamente. Por lo tanto, la CA se considera adecuada para aplicaciones energéticas. Considerando que, CNF es un mejor candidato para aplicaciones de energía.

El precursor de titanio óptimo para la fabricación de una capa compacta de TiO2 para células solares de perovskita Aptitud ecológica en la síntesis y estabilización de nanopartículas de cobre:actividades catalíticas, antibacterianas, citotóxicas y antioxidantes

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias