Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB

Teorema de Tellegen:guía paso a paso con ejemplos resueltos

¿Qué es el Teorema de Tellegen?

Teorema de Tellegen fue publicado por un ingeniero eléctrico e inventor holandés Bernard D.H. Tellegen en 1952. Este teorema es el más importante y fundamental entre otros teoremas en el análisis de redes. La mayoría de los demás teoremas se derivan de este teorema.

El teorema de Tellegen depende de la ley de Kirchhoff. Por lo tanto, este teorema se puede aplicar a la red que obedece la ley de Kirchhoff. Este teorema se puede aplicar a la amplia gama de redes que tienen elementos lineales o no lineales, variables en el tiempo o no variables, pasivos o activos.

El teorema de Tellegen establece que;

El teorema de Tellegen funciona según el principio de la ley de conservación de la energía. Este teorema se usa en aplicaciones químicas y biológicas para encontrar el comportamiento dinámico de la red física. En el procesamiento de señales, este teorema se usa para diseñar filtros.

• Publicación relacionada:Teorema de Thevenin. Guía paso a paso con ejemplo resuelto

Ecuación matemática

Para un análisis general del teorema, consideramos el número 'n' de elementos que se dan en la red. La corriente instantánea que pasa a través del elemento es i₁ , yo₂ , yo₃ , …., i_n . Y el voltaje instantáneo de esta rama es v₁ , v₂ , v₃ , …., v_n .

Por lo tanto, la corriente y el voltaje instantáneos del elemento-1 son i₁ y v₁ . La potencia instantánea (p₁ ) consumida por este elemento es v₁ yo₁ .

p ₁ =v ₁ yo ₁

El poder instantáneo del elemento-2 es (p ₂ );

p ₂ =v ₂ yo ₂

Del mismo modo, el poder instantáneo de n ^th elemento es (p _n );

p_n =v_n i_n

Según el teorema de Tellegen, la suma de todas las potencias instantáneas es cero. Significa que necesitamos sumar todas las potencias instantáneas p₁ , p₂ , p₃ , …., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ yo ₁ +v ₂ yo ₂ + v ₃ yo ₃ + … + v_n i_n  = 0

En forma general, podemos escribir la ecuación anterior para el k ^ésimo rama;

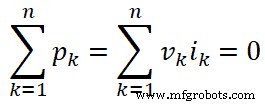
Dónde,

• n =número total de sucursales en la red
• v_k =voltaje instantáneo de k ^th rama
• i_k =corriente instantánea de k ^th rama
• p_k =potencia instantánea de k ^th rama

Ahora, considere la siguiente figura como la rama AB es igual a la rama k.

Por lo tanto, el voltaje instantáneo v_k ;

v_k =v_a – v_b

Y la corriente instantánea que pasa por la rama (a a b) es i_k ;

i_k =i_ab

Entonces, la potencia instantánea p_k es;

p_k =v_k i_k =(v_a –v_b ) i_ab ..... (1)

Ahora, consideramos la dirección opuesta de la corriente instantánea (b a a);

i_ab =– i_ab

Voltaje instantáneo;

v_k =v_b – v_a

La potencia instantánea p_k es;

p_k =v_k i_k =(v_b –v_a ) yo_ba ..... (2)

La suma de las ecuaciones 1 y 2;

2v_k i_k =(v_a –v _b ) yo _ab + (v_b – v_a ) i_ba

v_k i_k =1/2 [(v_a –v _b ) yo _ab + (v_b – v_a ) yo_ba ] ….. (3)

Esta ecuación se puede escribir como se muestra a continuación para n ramas;

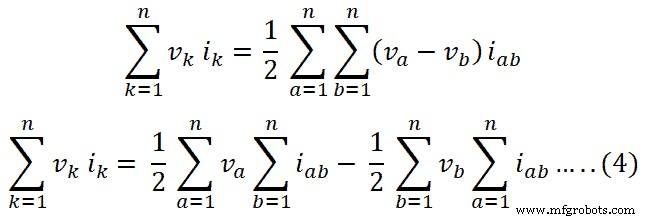
Según la ley de corriente de Kirchhoff, la suma algebraica de la corriente es cero en un nodo del circuito.

Por lo tanto,

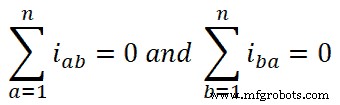
Si ponemos este valor en la ecuación-4, obtenemos;

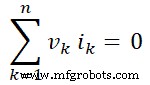
Por lo tanto, se demuestra que la suma de la potencia entregada a la red es cero. Por tanto, queda probado el teorema de Tellegen. También se describe que la suma de potencia absorbida por los elementos de la red es igual a la suma de potencia entregada por las fuentes.

• Publicación relacionada: Teorema de Norton. Guía paso a paso con ejemplo resuelto

Pasos a Seguir para el Teorema de Tellegen

Necesitamos seguir los pasos a continuación para resolver cualquier red eléctrica por el teorema de Tellegen.

Paso 1: Necesitamos encontrar un número de ramas en la red eléctrica dada. Luego encuentre la disipación de energía a través de cada rama. Para encontrar la potencia, necesitamos encontrar el voltaje o la corriente de esa rama utilizando cualquier método de análisis convencional.

Paso 2: Encuentra la potencia instantánea de cada rama.

Paso 3: El ramal que tiene una fuente de energía que se considera como ramal suministrador de energía. Y la rama que tiene otros elementos se considera como una rama que absorbe energía. Ahora identifique la rama de suministro de energía y la rama de absorción de energía.

Paso 4: Suponga un signo positivo en la rama que entrega energía y una caída de voltaje negativa en la rama que absorbe energía. También puede asumir signos inversos. Pero no puede cambiar a lo largo del ejemplo.

Paso 5: Para justificar el teorema de Tellegen, debemos sumar todas las potencias calculadas a partir de todas las ramas. Y esta suma siempre es cero.

• Publicación relacionada: Análisis del circuito SUPERMESH:paso a paso con ejemplo resuelto

Entendamos con un ejemplo.

Ejemplo resuelto del teorema de Tellegen

Ejemplo #1

Justifica el teorema de Tellegen para la siguiente red.

Solución:

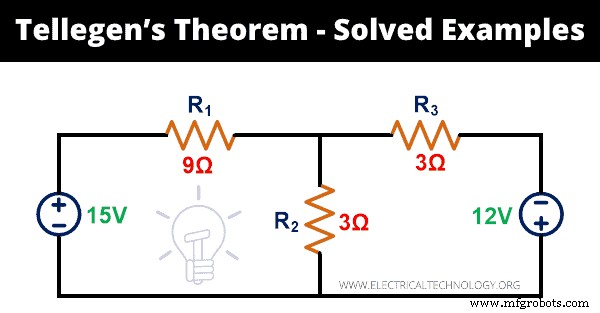
Paso 1: La red de circuito dada tiene 5 ramas. Para calcular la potencia instantánea, necesitamos encontrar la corriente que pasa por cada rama. Para eso, aplicaremos KVL a la red.

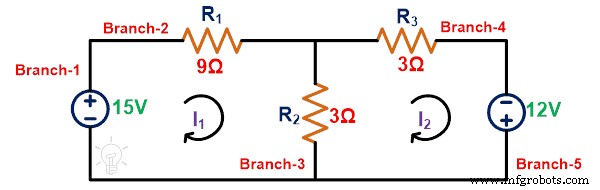
Aplicar KVL al loop-1;

15 =12yo ₁ – 3yo ₂

Aplicar KVL al loop-2;

12 =– 3yo ₂ + 6yo ₂

Resolviendo las ecuaciones anteriores, podemos encontrar los valores de la corriente de bucle I₁ y yo₂ . Y estos valores son;

Yo ₁ =2A

Yo ₂ =3A

Paso 2: La corriente que pasa por la rama-3 es;

Yo _{1 2} =yo ₂ – Yo ₁ =3 – 2 =1A

Tenemos corriente fluyendo a través de todas las ramas. Ahora, encuentra el poder de cada rama.

P ₁ =VI ₁ =15x2 =30W

P ₂ =R ₁ yo ₁ ² =9x4 =36W

P ₃ =R ₁ yo ₁₂ ² =3x1 =3W

P ₄ =R ₃ yo ₂ ² =3x9 =27W

P ₅ =VI ₂ =12x3 =36W

Paso 3: Hay dos ramas que tienen fuentes. Estas ramas son ramas que entregan energía y las otras tres ramas son ramas que absorben energía.

Aquí, para este ejemplo, asumimos que el signo de la rama que entrega energía es positivo y el signo de la rama que absorbe energía es negativo. Por lo tanto, las ramas 1 y 5 son ramas que entregan energía y otras ramas son ramas que absorben energía.

Paso 4: El signo del poder P₁ y P₅ es positivo (ramas que entregan energía) y el signo de P₂ , P₃ , y P₄ es negativo (ramas que absorben energía).

Paso 5: Ahora, necesitamos encontrar una suma del poder disipado por todas las ramas.

P ₁ – P ₂ – P ₃ – P ₄ + P ₅ =30W – 36W – 3W – 27W + 36W =0W

Entonces, la suma de la potencia instantánea es cero. Y por lo tanto, este teorema está probado.

• Publicación relacionada:Análisis del circuito SUPERNODO:paso a paso con ejemplo resuelto

Ejemplo #2

Encuentre el voltaje a través de la fuente de corriente de 6A usando el teorema de Tellegen.

Solución:

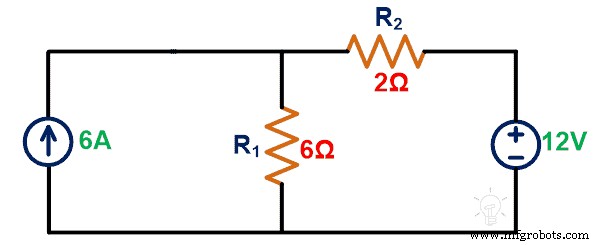
Paso 1: Necesitamos calcular los pasos de voltaje o corriente a través del elemento. Para eso, aplicamos KCL o KVL a la red dada.

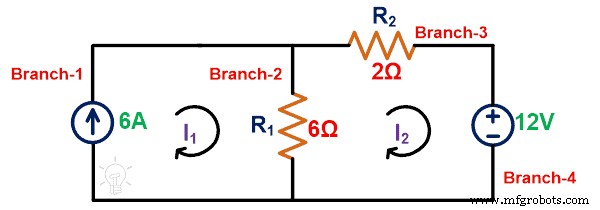
Aplicar KVL al loop-2;

-12 =8I ₂ – 6yo ₁

Los pasos actuales a través de la rama que tiene la fuente actual son I ₁;

Yo ₁ =6A

Coloca este valor en la ecuación anterior;

-12 =8I ₂ – 6(6)

-12 =8I ₂ – 36

36 – 12 =8I ₂

24 =8I ₂

Yo ₂ =3A

Paso 2: La corriente pasa por la rama-2 es;

Yo ₁₂ =yo ₁ – Yo ₂ =6 – 3 =3A

Ahora, encuentre el poder de cada rama;

P ₁ =VI ₁ =V x6 =6xV

P ₂ =R ₁ yo ₁₂ ² =6x9 =54W

P ₄ =R ₂ yo ₂ ² =2x9 =18W

P ₄ =VI ₂ =-12x3 =-36W

Paso 3: Aquí, dos ramas que tienen fuentes de energía. Por lo tanto, tenemos que considerar estas ramas como ramas que entregan energía. Y pon el signo positivo a la potencia instantánea.

Las otras dos ramas solo tienen resistencias. Por lo tanto, estas ramas son ramas que absorben energía y le dan el signo negativo a la potencia instantánea.

Paso 4: Potencia P₁ y P₄ tienen signo positivo y potencia P₂ y P3 tienen signo negativo.

Paso 5: Ahora, necesitamos sumar toda la potencia instantánea.

P ₁ – P ₂ – P ₃ + P ₄ =0W

P ₁ – 54 – 18 + 36 =108W

La potencia entregada por la fuente de corriente de 6A es de 108W. Por lo tanto, el voltaje a través de la fuente de corriente se calcula mediante;

P ₁ =VI

108W =V x 6A

V =18V

Por lo tanto, el voltaje en la fuente de corriente es de 18 V.

• Publicación relacionada: Teorema de transferencia de potencia máxima para circuitos de CA y CC

Análisis y simulación del teorema de Tellegen usando MATLAB  

Objetivo:

Pruebe el teorema de Tellegen para el diagrama de circuito dado en el ejemplo anterior.

Requisito: MATLAB

Teoría:

Según el teorema de Tellegen, la potencia instantánea sumatoria de todas las ramas es igual a cero. Para probar este teorema, necesitamos calcular la potencia instantánea de todas las ramas.

Para encontrar la potencia instantánea, necesitamos calcular el voltaje o la corriente de todas las ramas. Para eso, podemos usar los teoremas KCL o KVL. Pero aquí usaremos el modelo MATLAB Simulink para encontrar la corriente y el voltaje.

Podemos usar otro software también como multisim, psim, etc. Construiremos un diagrama de circuito en el modelo de Simulink. Por el modelo de Simulink, puede encontrar el voltaje y la corriente de cada rama.

Después de eso, puedes encontrar la potencia instantánea a partir del voltaje y la corriente. Puede encontrar directamente la potencia instantánea de algún software.

Modelo MATLAB Simulink

La siguiente figura muestra el diagrama de circuito del ejemplo anterior.

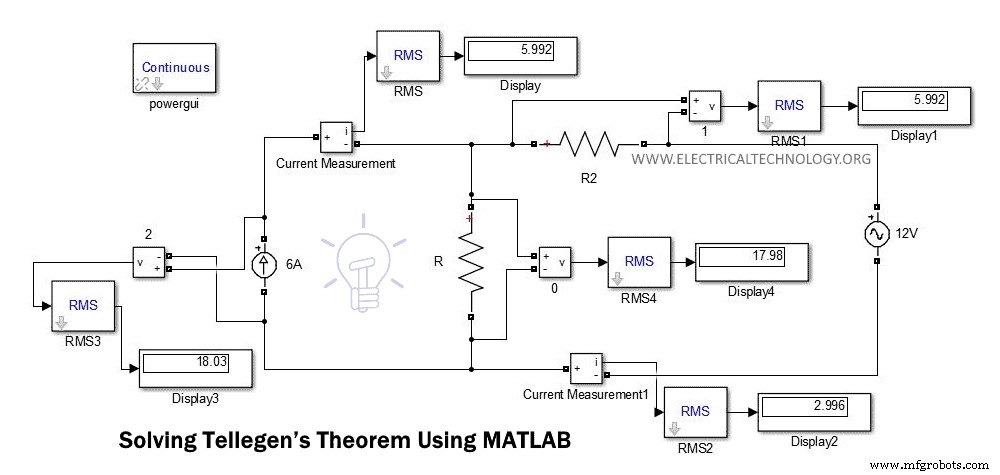
En esta figura, podemos encontrar directamente el voltaje y la corriente de la pantalla. Puede comparar estos valores calculando el voltaje y la corriente con la ayuda de KCL o KVL.

Cálculo

Después de calcular el voltaje o la corriente, puedes encontrar la potencia instantánea. O puede encontrar directamente la potencia instantánea del software. Todo lo que necesitamos es energía instantánea. Y después de eso, necesitamos agregar todos los poderes.

La suma de las potencias siempre es cero. Para este ejemplo, comparamos el valor del voltaje y la corriente encontrados en Simulink y los mismos valores calculados en el ejemplo anterior usando KVL y KCL. Estos valores son los mismos.

Estos valores también se calculan conectando resistencias y fuentes en la placa de prueba. Y podemos medir los pasos de voltaje y corriente a través de todas las ramas con la ayuda de un voltímetro y un amperímetro.

Por lo tanto, queda demostrado el teorema de Tellegen.

• Publicación relacionada:Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto

Aplicación del Teorema de Tellegen

Este teorema es muy fundamental y se usa ampliamente en el análisis de circuitos. Hay muchas aplicaciones de este teorema. Algunas aplicaciones se enumeran a continuación.

• Para diseñar los filtros, este teorema es muy útil en las aplicaciones de procesamiento de señales digitales.
• Para determinar la estabilidad de las plantas químicas, este teorema se usa en ingeniería química.
• Este teorema se aplica al sistema agrupado que tiene elementos lineales-no lineales, activo-pasivo, variables en el tiempo/invariantes en el tiempo.
• Este teorema se usa en el proceso biológico.
• Se utiliza en topología y análisis de reacciones estructurales.
• También se utiliza para encontrar el comportamiento dinámico de la red física.

Tutoriales de análisis de circuitos eléctricos relacionados:

• Teorema de superposición:análisis de circuito con ejemplo resuelto
• Calculadora de la regla de Cramer:sistema de 2 y 3 ecuaciones para circuitos eléctricos
• Puente de Wheatstone:circuito, trabajo, derivación y aplicaciones
• Calculadoras de ingeniería eléctrica y electrónica
• Más de 5000 fórmulas y ecuaciones de ingeniería eléctrica y electrónica