Teorema de Superposición – Análisis de Circuito con Ejemplo Resuelto

Teorema de superposición:guía paso a paso con ejemplo resuelto

¿Qué es el teorema de superposición?

El Teorema de superposición se utiliza para resolver redes complejas con varias fuentes de energía. Es un concepto importante determinar el voltaje y la corriente a través de los elementos calculando el efecto de cada fuente individualmente. Y combine el efecto de todas las fuentes para obtener el voltaje y la corriente reales del elemento del circuito.

El teorema de la superposición establece que;

En otras palabras, consideraremos solo una fuente independiente actuando a la vez. Por lo tanto, debemos eliminar otras fuentes. Las fuentes de voltaje están en cortocircuito y las fuentes de corriente están en circuito abierto para fuentes ideales. Si se proporciona la resistencia interna de las fuentes, debe considerar el circuito.

El teorema de superposición solo se aplica al circuito que sigue la ley de Ohm.

• Publicación relacionada: Teorema de Thevenin. Guía paso a paso con ejemplo resuelto

¿Cuándo usar el teorema de superposición?

La red debe seguir los siguientes requisitos para aplicar el teorema de superposición.

• Los componentes utilizados en el circuito deben ser lineales. Significa que, para las resistencias, el flujo de corriente es proporcional al voltaje; para los inductores, el enlace de flujo es proporcional a la corriente. Por lo tanto, la resistencia, el inductor y el capacitor son elementos lineales. Pero el diodo, el transistor no es un elemento lineal.
• Los componentes del circuito deben ser elementos bilaterales. Significa que la magnitud de la corriente es independiente de la polaridad de las fuentes de energía.
• Con la ayuda del teorema de superposición, podemos encontrar la corriente que pasa a través de un elemento, la caída de tensión de la resistencia y la tensión de nodo. Pero no podemos encontrar el poder disipado del elemento.

• Publicación relacionada: Teorema de Norton. Guía paso a paso con ejemplo resuelto

Pasos a Seguir para el Teorema de Superposición

Paso-1 Descubra una serie de fuentes independientes disponibles en la red.

Paso 2 Elija cualquier fuente y elimine todas las demás fuentes. Si la red consta de alguna fuente dependiente, no puede eliminarla. Permanece como está durante todo el cálculo.

Si ha considerado que todas las fuentes de energía son fuentes ideales, no necesita considerar la resistencia interna. Y fuente de voltaje de cortocircuito directo y fuente de corriente de circuito abierto. Pero en caso de que se dé la resistencia interna de las fuentes, debe reemplazar la resistencia interna.

Paso 3 Ahora, en un circuito, solo está presente una fuente de energía independiente. Necesita encontrar una respuesta con una sola fuente de energía en el circuito.

Paso 4 Repita los pasos 2 y 3 para todas las fuentes de energía disponibles en la red. Si hay tres fuentes independientes, debe repetir estos pasos tres veces. Y cada vez obtienes algún valor de la respuesta.

Paso 5 Ahora, combine todas las respuestas por suma algebraica obtenida por fuentes individuales. Y obtendrá un valor final de respuesta para un elemento particular de una red. Si necesita encontrar una respuesta para otros elementos, debe seguir estos pasos nuevamente para ese elemento.

• Publicación relacionada: Análisis del circuito SUPERMESH:paso a paso con ejemplo resuelto

Ejemplo resuelto del teorema de la superposición

Ejemplo:

Comprendamos el funcionamiento del teorema de superposición con un ejemplo. Encuentre la corriente (I_L ) pasa a través de la resistencia de 8 Ω en la red dada usando el teorema de superposición.

Solución:

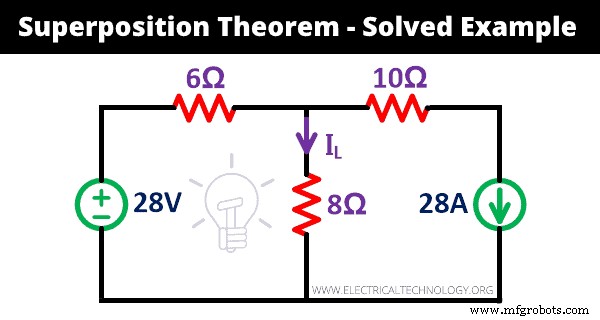
Paso-1 Como se muestra en la red anterior, se proporciona una fuente de voltaje y una fuente de corriente. Por lo tanto, necesitamos repetir el procedimiento dos veces.

Paso 2 Primero, consideramos que la fuente de voltaje de 28 V está presente en la red. Por lo tanto, debe eliminar la fuente de corriente mediante terminales de circuito abierto. Como aquí, consideramos la fuente de corriente como una fuente de corriente ideal. Por lo tanto, no necesitamos conectar la resistencia interna.

El circuito restante es como se muestra en la siguiente figura.

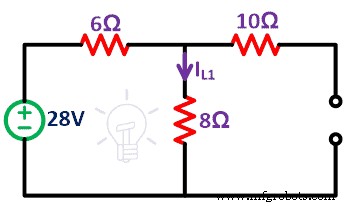
Paso 3 Encuentre la corriente (I_L1 ) pasa a través de una resistencia de 8Ω. Solo da el efecto de una fuente de voltaje.

Debido al circuito abierto de una fuente de corriente, no pasa corriente a través de la resistencia de 10 Ω. Entonces, la red consta de un solo bucle.

Aplicar KVL al bucle;

28 =6yo _{L 1} + 8yo _{L 1}

28 =14I _{L 1}

Yo _{L 1} =28/14

Yo _{L 1} =2A

Paso 4 Ahora, repetimos el mismo procedimiento para la fuente actual. En esta condición, eliminamos la fuente de tensión mediante un cortocircuito. Un circuito restante es como se muestra en la siguiente figura.

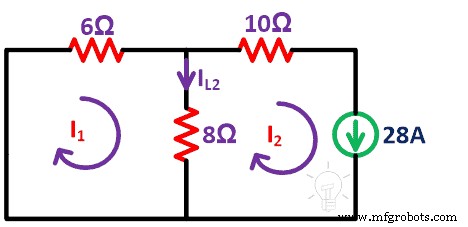
Aquí, tenemos que considerar dos bucles. Yo₁ y yo₂ son corrientes de bucle. Y encuentre el I_L2 actual .

Aplicar KVL al loop-1;

0 =6I ₁ + 8yo ₁ – 8yo ₂

14Yo ₁ – 8yo ₂ =0

La corriente que pasa por el loop-2 se calcula a partir de la fuente de corriente. Y será;

Yo ₂ =28A

Coloca este valor en la ecuación anterior;

14Yo ₁ – 8 (28) =0

Yo ₁ =16A

Ahora, la rama de resistencia de 8Ω es común en ambos bucles. Entonces, necesitamos encontrar la corriente resultante (I_L2 ) pasa a través de la resistencia de 8Ω.

Yo _{L 2} =yo ₁ – Yo ₂

Yo _{L 2} =16 – 28

Yo _{L 2} =-12A

Paso 5 Ahora, combinamos el efecto de ambas fuentes por suma algebraica de corriente. Entonces, la corriente total que pasa a través de la resistencia de 8Ω es I_L . Aquí, la dirección de la corriente es lo más importante. Actual I_L2 tiene un signo menos. Significa que durante la fuente de 28A, la corriente fluye en dirección opuesta. Y no podemos cambiar la dirección. Esa es la razón por la que al combinar todas las fuentes, estamos haciendo una suma algebraica.

Yo _L =Yo_{L 1} – Yo_{L 2}

Yo _L =2 + (-12)

Yo _L =-10A

Aquí, hemos asumido que la corriente pasa a través de la resistencia de 8Ω en la dirección de la flecha que se muestra en la figura. El signo menos muestra la dirección opuesta. Y la cantidad de corriente es 8A.

• Publicación relacionada:Análisis del circuito SUPERNODO:paso a paso con ejemplo resuelto

Experimento del teorema de superposición

El experimento del teorema de superposición se puede realizar siguiendo los pasos a continuación.

Apuntar

Determina la corriente que fluye a través de las resistencias y verifica el teorema de superposición.

Componentes necesarios

Fuente de CC, resistencias, multímetros de CC, cables de conexión, placa de pruebas, etc.

Teoría

El teorema de superposición se usa en el análisis de circuitos para encontrar la corriente y el voltaje a través de los elementos en un circuito dado. Este teorema es útil cuando el número de fuentes es mayor.

Según el teorema de superposición, la respuesta de los elementos es una suma algebraica de la respuesta de las fuentes de energía individuales.

Primero, calcularemos los pasos de corriente a través de las resistencias en una red determinada. Cuando todas las fuentes están conectadas. Después de eso, eliminamos fuentes y encontramos corrientes para fuentes individuales. Por fin, la suma de la corriente medida de las fuentes individuales es similar a las medidas de corriente con todas las fuentes conectadas.

Procedimiento

Consideramos el circuito bilateral lineal que se muestra en la siguiente figura.

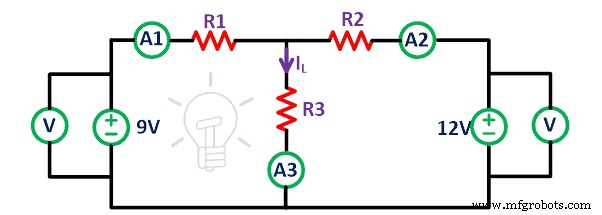
Conecte todos los elementos en la placa de prueba como se indica en el circuito anterior usando cables de conexión. Conecte el amperímetro con todas las resistencias para encontrar la corriente que pasa a través de las resistencias. Aquí, tenemos dos fuentes de voltaje.

En el primer caso, mida la corriente que pasa a través de todas las resistencias cuando ambas fuentes de voltaje están presentes en el circuito. La corriente que fluye a través de la resistencia R₁ , R₂ y R₃ soy yo ₁ , yo ₂ y yo ₃ respectivamente.

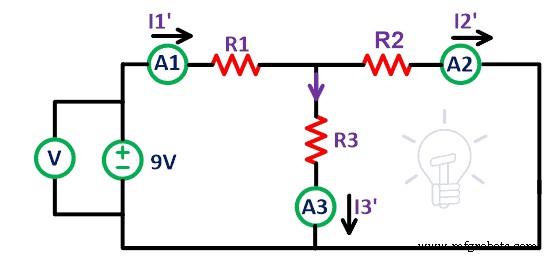
Ahora retire la fuente de voltaje de 12V del circuito. Cortocircuite los terminales A' y B' como se muestra en la figura anterior. Aquí hemos supuesto que las fuentes de voltaje son ideales. Por lo tanto, no es necesario conectar una resistencia interna. Ahora, mida la corriente I _1′ , yo _2′ y yo _3′ que es la corriente que pasa a través de la resistencia R1, R2 y R3 respectivamente.

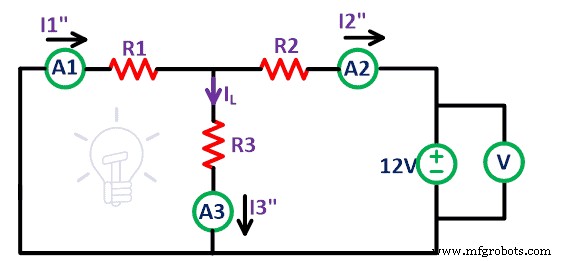
Del mismo modo, retire la fuente de voltaje de 9 V y el circuito restante es como se muestra en la figura anterior. Nuevamente, mida la corriente que fluye a través de todas las resistencias y asígnele el nombre I _{1 “} , yo _{2 “} y yo _{3 “} .

• Publicación relacionada: Teorema de transferencia de potencia máxima para circuitos de CA y CC

Coloque todos los valores en la siguiente tabla de observación.

Tabla de observación

Conexión de origen	R1	R2	R3
Ambas fuentes están conectadas	Yo 1	Yo 2	Yo 3
Solo 12V está conectado	Yo 1′	Yo 2′	Yo 3′
Solo 9V está conectado	Yo 1″	Yo 2″	Yo 3″

Cálculo :

Yo ₁ =yo _1′ + yo _1″

Yo ₂ =yo _2′ + yo _2″

Yo ₃ =yo _3′ + yo _3″

Para verificar el teorema de superposición, comparamos la suma algebraica de los pasos de corriente a través de las resistencias cuando una fuente individual está conectada con la corriente medida cuando ambas fuentes están conectadas en un circuito.

Si el cálculo anterior satisface, podemos probar el teorema de superposición.

Conclusión

En este experimento, podemos demostrar que la corriente que pasa a través de la resistencia es una suma algebraica de la corriente cuando se conecta una fuente de energía individual. Y prueba el teorema de superposición.

• Publicación relacionada:Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto

Aplicación del teorema de superposición

• El teorema de superposición se puede usar para redes de CA y CC.
• Cuando el número de fuentes independientes es mayor, es fácil encontrar una respuesta de la red.
• Ayuda a calcular los pasos de corriente y el voltaje a través del elemento al calcular el efecto de cada fuente de energía individualmente. Y después podemos determinar el efecto combinado en elementos de todas las fuentes.

Inconveniente del teorema de superposición

• El teorema de superposición no se puede aplicar al circuito que tiene solo una fuente dependiente. Necesitaba al menos dos fuentes independientes.
• Este teorema solo es aplicable a la red que consta de elementos lineales. No se puede aplicar a los elementos no lineales como un diodo, un transistor, etc.
• No podemos calcular la potencia con este teorema. Como la potencia es proporcional al cuadrado del voltaje y la corriente, ya que se vuelve no lineal.
• Este teorema no es aplicable en una condición en la que la resistencia varía con el voltaje y la corriente. Para todas las fuentes de energía, el valor de la resistencia debe permanecer constante.
• Este teorema solo es aplicable a los elementos bilaterales. Si la respuesta de la red depende de la dirección de la corriente, este teorema no es aplicable.

Tutoriales de análisis de circuitos eléctricos relacionados:

• Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB
• Calculadora de la regla de Cramer:sistema de 2 y 3 ecuaciones para circuitos eléctricos
• Puente de Wheatstone:circuito, trabajo, derivación y aplicaciones
• Calculadoras de ingeniería eléctrica y electrónica
• Más de 5000 fórmulas y ecuaciones de ingeniería eléctrica y electrónica