Regla del divisor de corriente (CDR):ejemplos resueltos para circuitos de CA y CC

División de corriente “CDR” para circuitos resistivos, inductivos y capacitivos

Qué ¿Cuál es la regla del divisor de corriente (CDR)?

Cuando varios elementos se conectan en paralelo, la corriente se divide en varios caminos paralelos. Y el voltaje es el mismo para todos los elementos que son iguales al voltaje de la fuente.

En otras palabras, cuando la corriente pasa por más de un camino paralelo (la regla del divisor de voltaje “VDR” o división de voltaje se usa para calcular el voltaje en los circuitos en serie), la división actual en cada camino. El valor de la corriente que pasa a través de una rama en particular depende de la impedancia de esa rama.

La regla del divisor de corriente o la regla de división de corriente es la fórmula más importante que se usa ampliamente para resolver circuitos. Podemos encontrar la corriente que pasa por cada rama si conocemos la impedancia de cada rama y la corriente total.

La corriente siempre fluye a través de la menor impedancia. Entonces, la corriente tiene una relación inversa con la impedancia. De acuerdo con la ley de ohm, la corriente que ingresa al nodo se dividirá entre ellos en proporción inversa a la impedancia.

Significa que la impedancia de menor valor tiene una corriente mayor ya que la corriente eligió la ruta de menor resistencia. Y la resistencia de mayor valor tiene la menor corriente.

Según los elementos del circuito, la regla del divisor de corriente puede describir resistencias, inductores y capacitores.

Regla del divisor de corriente para circuitos resistivos

Para comprender la regla del divisor de corriente resistiva, tomemos un circuito en el que las resistencias están conectadas en paralelo. El diagrama del circuito se muestra en la siguiente figura.

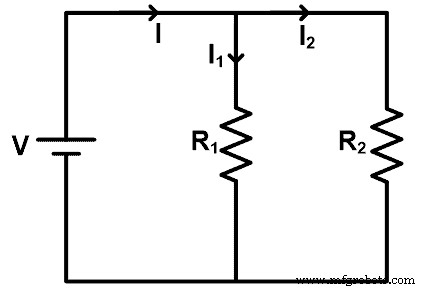
En este ejemplo, una fuente de CC alimenta todas las resistencias. El voltaje de las resistencias es el mismo que el voltaje de la fuente. Pero debido a la conexión en paralelo, la corriente se divide en diferentes caminos. La corriente se divide en cada nodo y el valor de la corriente depende de la resistencia.

Podemos encontrar directamente el valor de la corriente que pasa a través de cada resistencia con la ayuda de la regla del divisor de corriente.

En este ejemplo, la corriente principal suministrada por la fuente es I. Y se divide en dos resistencias R₁ y R₂ . La corriente pasa a través de la resistencia R₁ soy yo₁ y la corriente pasa por la resistencia R₂ es yo₂ .

Como las resistencias están conectadas en paralelo. Entonces, la resistencia equivalente es R_eq .

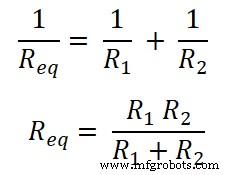
Ahora, según la ley de Ohm;

V =I R_eq

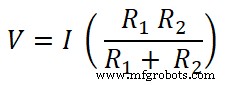
Ambas resistencias están conectadas en paralelo con una fuente de CC. Por lo tanto, el voltaje a través de la resistencia es el mismo que el voltaje de la fuente. Y la corriente que pasa por la resistencia R₁ soy yo₁ .

Entonces, para la resistencia R₁;

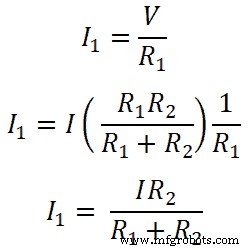
Del mismo modo, para la resistencia R₂;

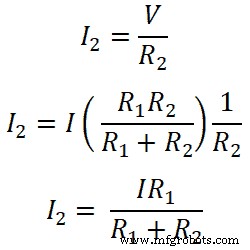
Entonces, esta ecuación muestra una regla divisoria de corriente para la resistencia conectada en paralelo. A partir de estas ecuaciones, podemos decir que la corriente que pasa a través de la resistencia es igual a la relación de multiplicación de la corriente total y la resistencia opuesta con la resistencia total.

Publicaciones relacionadas:

• Teorema de Thevenin. Guía paso a paso con ejemplo resuelto
• Teorema de Norton. Guía paso a paso con ejemplo resuelto

Regla del divisor de corriente para circuitos inductivos

Cuando los inductores están conectados en paralelo, podemos aplicar la regla del divisor de corriente para encontrar la corriente que pasa a través de cada inductor. Para comprender la regla del divisor de corriente, tomamos un circuito en el que los inductores están conectados en paralelo como se muestra en la figura a continuación.

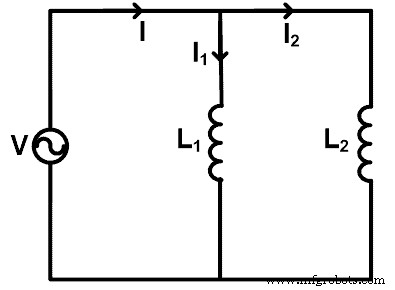
Aquí, dos inductores (L₁ y L₂ ) están conectados en paralelo con una fuente de voltaje V. La corriente total que pasa a través de la fuente es I amperio. La corriente pasa por el inductor L₁ soy yo₁ y la corriente pasa por el inductor L₂ es yo₂ .

Ahora, necesitamos encontrar las ecuaciones para la corriente I₁ y yo₂ . Para eso, encontraremos la inductancia equivalente L_eq;

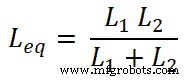
Sabemos que la corriente total que pasa por el circuito es I y es igual a;

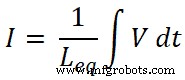
Entonces,

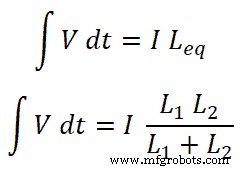
Ahora, para el inductor L₁ , la corriente que pasa a través de este inductor es I₁;

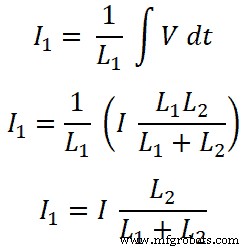
Para inductor L₂;

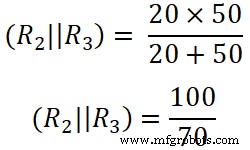
La regla de división de corriente para el inductor es la misma que la regla de división de corriente para las resistencias.

Regla del divisor de corriente para circuitos capacitivos

Cuando los capacitores están conectados en paralelo, podemos encontrar la corriente que pasa a través de cada capacitor usando la regla del divisor de corriente. Para entender la regla del divisor de corriente para el capacitor, tomamos un ejemplo en el que los capacitores están conectados en paralelo como se muestra en la siguiente figura.

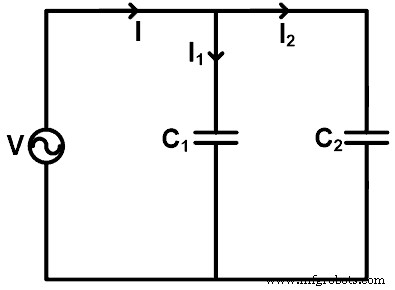
Aquí, dos condensadores (C₁ y C₂ ) están conectados en paralelo con una fuente de voltaje V. La corriente pasa a través del capacitor C₁ es yo_1, y la corriente pasa por el capacitor C₂ es yo₂ . La corriente total suministrada a través de la fuente es I.

Ahora, necesitamos encontrar las ecuaciones para la corriente I₁ y yo₂ . Para eso, encontraremos la capacitancia equivalente C_eq;

C_eq =C ₁ + C ₂

Conocemos la ecuación de la corriente que pasa a través del capacitor. Y la ecuación para la corriente total suministrada por la fuente es;

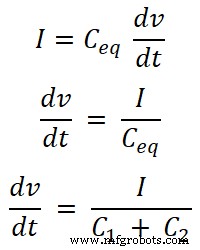
Para condensador C₁ , la corriente que pasa por este capacitor es I₁;

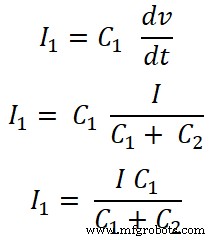
Para condensador C₂;

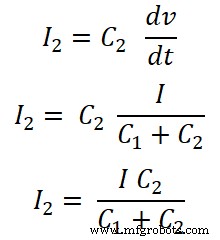
La regla del divisor de corriente para el capacitor es ligeramente diferente de la regla del divisor de corriente para el inductor y la resistencia.

En la regla del divisor de corriente del capacitor, la corriente que pasa a través de un capacitor es una relación de la corriente total multiplicada por ese capacitor a la capacitancia total.

Ejemplos resueltos para circuitos de CA y CC usando CDR

Regla de buzo actual para circuito DC

Ejemplo:1

Encuentre los pasos de corriente a través de cada resistencia por la regla divisoria de corriente para la red dada.

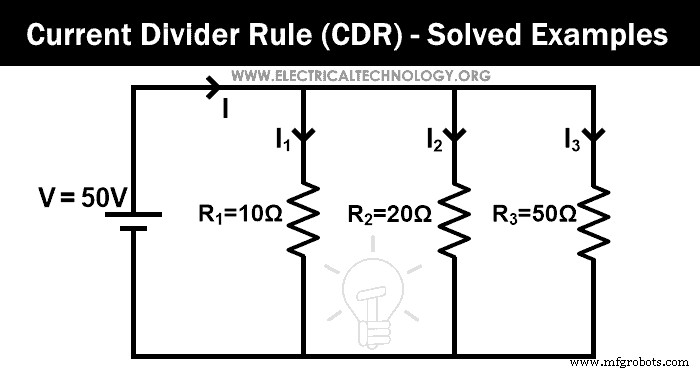
En este ejemplo, tres resistencias están conectadas en paralelo. Primero, encontramos la resistencia equivalente.

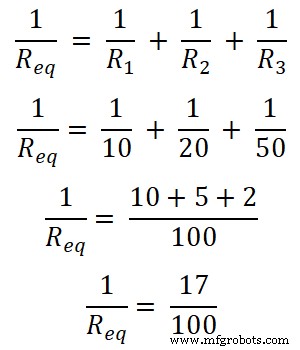
R_eq = 100/17

R_eq = 5,882 Ω

La corriente total suministrada por la fuente es I. Entonces, de acuerdo con la ley de ohm;

V =I R_eq

50V =yo (5.882Ω)

I = 50 V/5,882 Ω

I = 8.5A

Ahora, aplicamos la regla del divisor de corriente a la primera resistencia (10 Ω), y la corriente que pasa a través de esta resistencia es I₁;

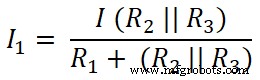
Aquí R₂ y R₃ están conectados en paralelo. Entonces, necesitamos encontrar la resistencia equivalente entre R₂ y R₃ .

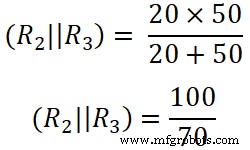
(R ₂ || R ₃ ) =14,285 Ω

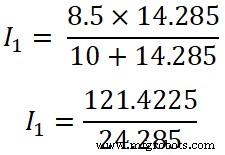
Yo ₁ =4,9999 ≈ 5 A

Del mismo modo, aplicamos la regla del divisor de corriente a la segunda resistencia (20 Ω), y la corriente que pasa a través de esta resistencia es I₂;

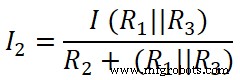
Aquí,

(R ₁ || R ₃ ) =8,33 Ω

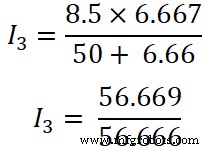
Yo ₂ =2,499 ≈ 2,5 A

Ahora, aplicamos la regla del divisor de corriente a la tercera resistencia (50 Ω), y la corriente que pasa a través de esta resistencia es I₃ .

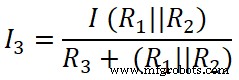
Aquí,

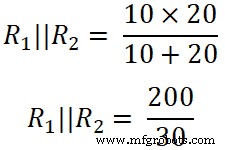
(R ₁ || R ₂ ) =6,66 Ω

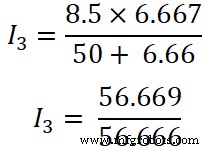
Yo ₃ =1,00 A

Entonces, la suma de las tres corrientes será;

Yo ₁ + yo ₂ + yo ₃ =5 + 2,5 + 1 =8,5 A

Y esta corriente es la misma que la corriente total suministrada por la fuente.

Regla de buzo actual para circuito de CA

Ejemplo-2

Considere un circuito de CA que tenga una resistencia y un capacitor conectados en paralelo como se muestra en la siguiente figura. Encuentre la corriente que pasa a través de la resistencia y el capacitor usando la regla del divisor de corriente. Considere la frecuencia de 60 Hz.

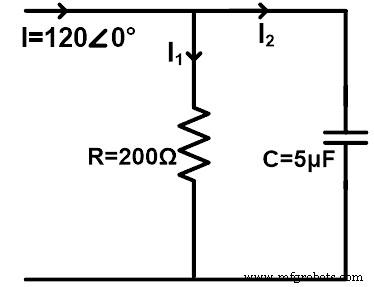
Z_R =200 Ω =200∠0°Ω

Z_C =1/(2 πf C) =1/(2 π 60(5×10 ⁶ ) )

Z_C =10 ⁶ / (600 π)

Z_C =530,78 ∠-90° Ω

Ahora, de acuerdo con la regla del divisor de corriente, la ecuación de la corriente que pasa a través de la resistencia es;

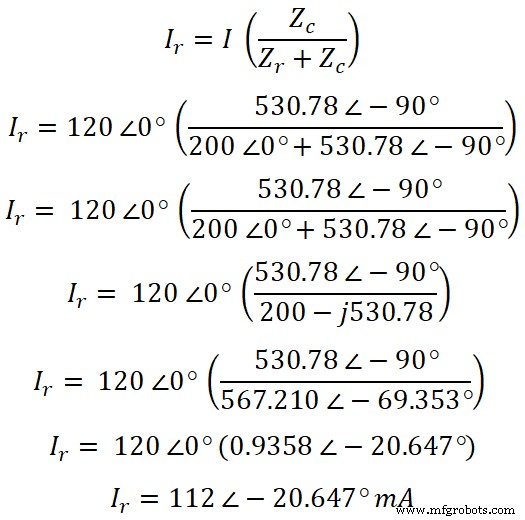
Ahora, de manera similar, podemos encontrar la corriente que pasa a través del capacitor. De acuerdo con la regla del divisor de corriente, la ecuación de la corriente que pasa a través del capacitor es;

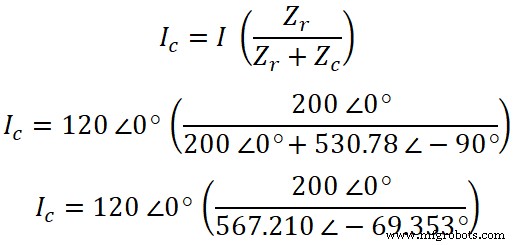
Yo_C =120 ∠0° (0,3526 ∠ 69,353°)

Yo_C =42,31 ∠ 69,353°

Si desea probar esta respuesta, puede agregar ambas corrientes. Y el valor de esta corriente es el mismo que el de la fuente de corriente.

Tutoriales de análisis de circuitos eléctricos relacionados:

• Teorema de compensación:prueba, explicación y ejemplos resueltos
• Teorema de sustitución:guía paso a paso con ejemplo resuelto
• Análisis del circuito del SUPERNODO:paso a paso con un ejemplo resuelto
• Análisis del circuito SUPERMESH:paso a paso con un ejemplo resuelto
• Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto
• Calculadora de la regla de Cramer:sistema de 2 y 3 ecuaciones para circuitos eléctricos
• Puente de Wheatstone:circuito, trabajo, derivación y aplicaciones
• Calculadoras de ingeniería eléctrica y electrónica
• Más de 5000 fórmulas y ecuaciones de ingeniería eléctrica y electrónica