Qué es el análisis de malla:procedimiento y sus ejemplos

En el campo de la electrónica, es más crucial analizar incluso los circuitos simples. Para el análisis de circuitos simples, se utilizan principios como el voltaje de Kirchhoff y la ley de corriente de Kirchhoff. Mientras que en la situación de circuitos complicados que tienen múltiples fuentes controladas de voltaje y corriente, debe haber herramientas adicionales junto con las leyes KVL y KCL. Solo con los principios KVL y KCL, el análisis resulta ser inexacto y tampoco confiable. Entonces, para ir con un análisis exacto y conocer las variables en esos circuitos, se deben implementar enfoques como mesh y nodal. Con estos métodos, se pueden conocer fácilmente variables como la corriente y los voltajes. Háganos saber claramente sobre el análisis de malla, análisis de súper malla en este artículo.

¿Qué es el análisis de malla?

La malla se considera un bucle que no tiene otros bucles dentro del circuito. Aquí, las corrientes de malla se utilizan como variables en lugar de las corrientes para conocer el análisis completo del circuito. Debido a esto, la técnica necesita un número mínimo de ecuaciones para resolver. El análisis de malla se implementa en los circuitos utilizando la ley de voltaje de Kirchhoff para conocer los valores de corriente desconocidos.

Esto también se denomina técnica de bucle de corriente de malla. Después de esto, los valores de voltaje también se pueden conocer mediante la implementación de la ley de Ohm. Una rama se considera como la ruta donde conecta dos nodos y se incluye con un elemento de circuito. Cuando una malla consta de una sola rama, la corriente de la rama se denomina corriente de malla. Mientras que cuando una malla consta de dos ramas, la corriente de la malla se considera como la suma o la diferencia de los dos bucles de la malla cuando están en caminos similares o opuestos.

Pasos

• Al conocer las variables de un circuito, existe un procedimiento a seguir para la implementación del análisis de malla y los pasos se pueden explicar de la siguiente manera:
• En la primera fase, busque las mallas y marque las corrientes de las mallas en sentido antihorario o en el sentido de las agujas del reloj.
• Observe la cantidad de flujo de corriente que fluye a través de cada elemento correspondiente a las corrientes de malla.
• Escriba todas las ecuaciones de malla para las mallas observadas. Las ecuaciones de malla se escriben aplicando la ley de Kirchhoff y luego aplicando la ley de Ohm
• Para averiguar las corrientes de malla, resuelva las ecuaciones de malla observadas según el paso 3.
• Con esto, el flujo de valores de corriente y voltaje a través de cada elemento del circuito se puede conocer mediante la aplicación de corrientes de malla.

Formulario general para configurar ecuaciones en análisis de malla

Tras la identificación de las mallas en el circuito, cada una consta de una ecuación. Las ecuaciones son el total de la caída de voltaje en todo el bucle de la corriente de malla. En los casos de circuitos, que tienen más de voltaje y corriente, la caída de voltaje se considera como la impedancia del circuito que se multiplica por la corriente de malla del bucle específico.

Cuando la fuente de voltaje existe interna al bucle, entonces el voltaje presente en la fuente se puede sumar o restar según la condición, ya sea la pérdida de voltaje o el aumento de voltaje para esa malla. Pero en la condición en la que la fuente actual no se encuentra entre las mallas, entonces la corriente de la malla considerará un valor negativo o positivo de la fuente según la dirección de la fuente de la corriente de la malla.

Método de corriente de malla

Con el circuito a continuación, el análisis del método de corriente de malla se puede conocer fácilmente. En el circuito, las corrientes de lazo I1 e I2 se aplican en el sentido de las agujas del reloj

Dependiendo de la dirección de la corriente de bucle, las polaridades de las caídas de voltaje tienen lugar en las resistencias R1, R2 y R3. Aquí, las corrientes I1 e I2 tendrán rutas de flujo de corriente opuestas debido a que la resistencia R2 comparte ambos bucles.

Entonces, se pueden conocer las dos polaridades de los voltajes. Mientras que en los escenarios prácticos, R2 se puede categorizar en dos fases, pero las corrientes de lazo son especialmente aplicables para aplicaciones de análisis. No hay impacto en las polaridades de las fuentes de voltaje porque son constantes.

Tras la aplicación de la ley de voltaje de Kirchhoff, se pueden escribir las dos ecuaciones siguientes

R2 (I1 - I2) + R1I1 =V1 - Derivado del bucle 1

R2 (I2 - I1) + R1I2 =-V2 - Derivado del bucle 2

Los términos similares en las ecuaciones anteriores se combinan y, una vez dispuestos, los mismos términos aparecen en una posición similar en cada ecuación. Cuando se conocen las corrientes de bucle, se pueden evaluar las corrientes de derivación. Las ecuaciones reorganizadas son:

I1 (R1 + R2) - I2R2 =V1 - Para el bucle 1

-I1R2 + (R2 - R3) I3 =-V2 - Para el bucle 2

Problemas resueltos del análisis de malla

Esta sección muestra los ejemplos resueltos de encontrar corriente en un circuito usando el método de corriente de malla .

En el circuito a continuación, averigüe la cantidad de voltaje que pasa por la fuente de corriente de 15 amperios mediante el método de análisis de malla. Siempre que todas sean fuentes actuales

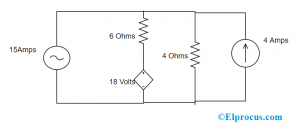
Según el circuito, existe la posibilidad de cambiar la fuente de voltaje a corriente usando una resistencia en paralelo. Para hacer esto, se coloca una resistencia en conexión en serie con la fuente de voltaje y la resistencia debe poseer el mismo valor que la fuente de voltaje y el voltaje es

Vs =IsRs =4 * 4 =16V

Averigüe las corrientes de rama (I1 e I2) para los bucles e indique las direcciones del flujo de corriente en ambos bucles.

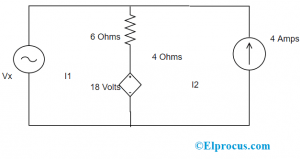
Luego, para cada malla (bucle), aplique la ley KVL

Malla - 1

Vx - (I1 - I2) - 18 =0

Aquí, I1 =15

Entonces, Vx + (6 * I2) =90

Malla - 2

18 - 6 (I2 - I1) - 4 * I2 - 16 =0

I2 =78/10

=7,8 amperios

Según la ecuación Mesh-1

Vx =90 - 44,4

Vx =45,6 V

Este es el ejemplo resuelto de resolución de dos mallas mediante análisis de corriente de malla

Aquí, necesitamos averiguar el voltaje y las corrientes de derivación. Considere el circuito a continuación.

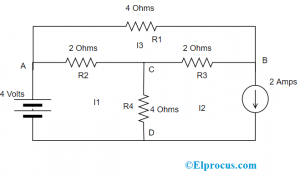
Mediante la aplicación de la ley KVL al primer bucle, obtenemos

V1 - R2 (I1 - I3) - R4 (I1 - I2) =0

4 - 2 (I1) - 2 (I3) - 4 (I1) - 4 (I2) =0

-2 (I3) - 6 (I1) =4

Al aplicar la ley KVL a la segunda malla, obtenemos

-Vc - R4 (I2 - I1) - R3 (I2 - I3) =0

-Vc =-4 (I1) + 6 (I2) - 2 (I3) =0

Como I2 =-2A, obtenemos

-Vc =-4 (I1) -12-2 (I3) =0

Al aplicar la ley KVL a la tercera malla, obtenemos

-R1 (I3) - R3 (I3 - I2) - R2 (I3 - I1) =0

Sustituyendo I2 =-2A

2 (I1) - 8 (I3) =0

Al resolver las ecuaciones de malla primera y tercera, obtenemos

I1 =4.46 y I3 =-0.615

Entonces, Vc =28.61V

Y la corriente de la rama es

Iac =I1 - I3

Iac =5.075 amperios

Este es el ejemplo resuelto de resolver tres mallas usando el análisis de corriente de malla

Estos son los ejemplos de muestra resueltos mediante análisis de malla. Un análisis exhaustivo de este concepto nos permite resolver también circuitos complejos.

Análisis de supermallas

Para el análisis de circuitos enormes y complejos, el análisis de supermallas sirve como el mejor enfoque que el análisis de mallas, porque en la supermallas habrá dos mallas que comparten un componente común como fuente de corriente.

Se sigue la misma técnica para el análisis de circuitos de supernodo como alternativa para el análisis de circuitos nodales porque este método simplifica esos circuitos complejos al cerrar el elemento de voltaje y minimizar el número de nodos de referencia para cada fuente de voltaje. En el análisis de supermallas, la fuente de corriente se encuentra dentro de la sección de supermallas, de modo que se pueden minimizar las mallas en una por cada fuente de corriente que estén presentes.

Cuando la fuente de corriente está presente en el permiso del circuito, es posible que no se considere una sola malla. Por otro lado, KVL se implementa solo para aquellas mallas en el circuito eléctrico modificado.

Consideremos un ejemplo de análisis de supermallas para una mejor comprensión.

Usando el análisis de supermallas, averigüe los valores de V3, i1, i2 e i3 para el circuito siguiente.

En la aplicación de KVL al Mesh-1, obtenemos

10i1 + 80 (i1 - i2) + 30 (i1 - i3) =80

Obtenemos 60i1 - 20i2 - 30i3 =80

Mediante la aplicación de la técnica de supermalla a Malla 2 y Malla 3, obtenemos

30 =40i3 + 30 (i3 - i1) + 20 (i2 - i1)

70i3 - 50i1 + 20i2 =30

La fuente de corriente individual que está en la supermalla corresponde a las corrientes de malla esperadas que son

15ix =i3 - i2

I3 =15ix + i2

Al resolver las tres ecuaciones anteriores, obtenemos

i1 =0,58 amperios, i2 =-6,16 amperios e i3 =2,6 amperios

Para encontrar V3, tenemos v3 =i3 * R3, entonces

V3 =2.6 * 40 =104V

Usos del análisis de malla

El uso principal del análisis de malla es para resolver circuitos planos para conocer los valores actuales en cualquier posición tanto en los circuitos eléctricos simples como en los complicados

El otro uso es que los cálculos normales para resolver ecuaciones son difíciles y se necesitan más fórmulas matemáticas, mientras que a través del análisis de malla, menos cálculos son suficientes.

El otro uso del análisis de corriente de malla es un puente de piedra de trigo desequilibrado. Para saber esto, considere el siguiente ejemplo

Como las proporciones de las resistencias, R1 / R4 y R2 / R5 no son iguales, podemos entender que habrá cierta cantidad de voltaje y flujo de corriente en R3. Como somos conscientes de que resolver este tipo de circuitos es complicado por el enfoque de la técnica general serie-paralelo, necesitamos otro enfoque para resolver esto.

Entonces, con respecto a eso, podemos aplicar el método de la corriente de rama, pero este método necesita seis corrientes de Ia a If, lo que lleva a trabajar en cualquier número de ecuaciones. Por lo tanto, esta complejidad se puede reducir fácilmente a través del método actual de Mesh, donde esto requiere solo unas pocas variables.