Teorema de Compensación – Prueba, Explicación y Ejemplos Resueltos

Prueba, Explicación, Experimento y Ejemplos Resueltos del Teorema de Compensación para el Análisis de Circuitos

Teorema de compensación

Al igual que en la teoría de redes, es importante conocer o estudiar el efecto del cambio de impedancia en una de sus ramas. Afectará el voltaje y las corrientes correspondientes de la red o circuito. El teorema de compensación da información sobre el cambio en la red.

El teorema de compensación funciona sobre el concepto básico de la ley de Ohm. De acuerdo con la ley de Ohm, cuando una corriente pasa a través de la resistencia, se produce una cierta caída de tensión en la resistencia. Esta caída de voltaje se opondrá al voltaje de la fuente.

Por lo tanto, conectamos una fuente de voltaje adicional en polaridad opuesta en comparación con el voltaje de la fuente y la magnitud es igual a la caída de voltaje. El teorema de compensación funciona sobre este concepto.

El teorema de compensación establece que,

• Publicación relacionada: Teorema de Thevenin. Guía paso a paso con ejemplo resuelto

Explicación del Teorema de Compensación

Para entender el teorema de compensación, considere la siguiente figura.

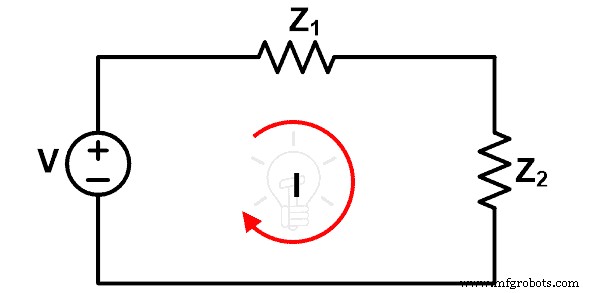
En esta figura, la fuente de voltaje V es un voltaje y una fuente independientes y dos impedancias Z₁ y Z₂ son elementos lineales o bilaterales. Por lo tanto, podemos aplicar el teorema de compensación a esta red. La corriente que pasa por el bucle es I.

Ahora, suponga que la impedancia Z₂ incrementado por ∆Z. Debido a este cambio, la corriente que pasa por el bucle cambia y es I’. El nuevo diagrama de circuito se muestra en la siguiente figura.

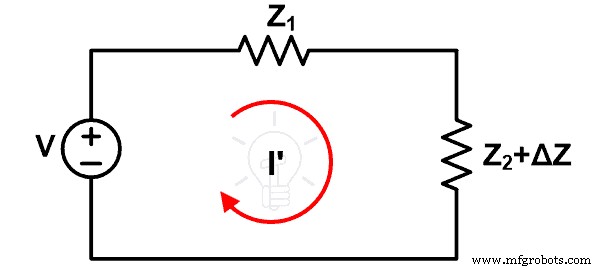
Debido al cambio de impedancia, el cambio de corriente dado por ∆I.

ΔYo =yo – Yo’

De acuerdo con el enunciado del teorema de compensación, podemos calcular directamente el cambio en el ∆I actual. Para eso, necesitamos modificar el circuito.

La primera modificación es que, conectar una fuente de voltaje de valor I∆Z en la rama de la cual se cambia la impedancia. Y la polaridad de esta fuente de voltaje es opuesta a la fuente principal. La fuente de voltaje recién agregada V_C se conoce como la fuente de compensación.

V_C =yo ΔZ

La segunda modificación es que necesitamos eliminar la fuente de voltaje anterior por su impedancia interna. Si consideramos una fuente de voltaje ideal, en esta condición, podemos eliminar esta fuente de voltaje cortocircuitando su terminal. Después de estas modificaciones, el circuito restante es como se muestra en la figura a continuación.

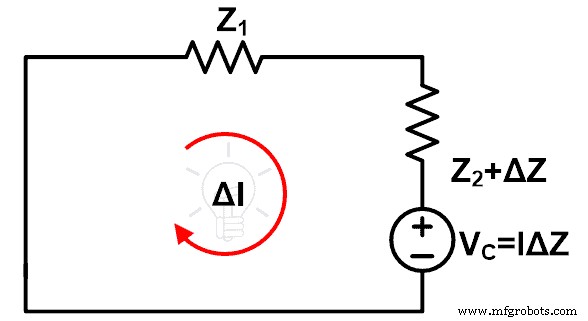
Al resolver el circuito anterior, podemos encontrar fácilmente el cambio en la corriente después del cambio en la impedancia.

• Publicación relacionada: Teorema de Norton. Guía paso a paso con ejemplo resuelto

Prueba del Teorema de Compensación

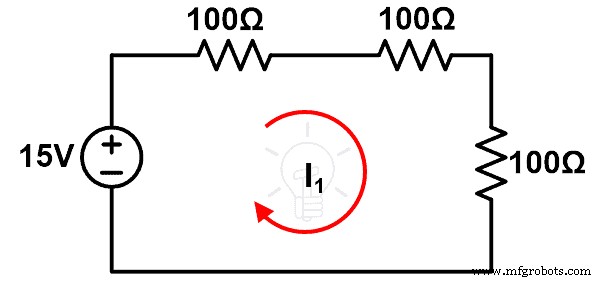
Considere el circuito dado en la figura-1. Calcular la corriente (I) que pasa por el bucle.

Aplicar KVL a la figura-1;

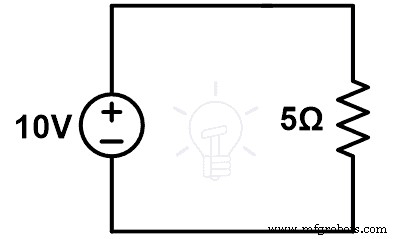
Ahora, hemos supuesto que la impedancia Z₂ se cambia por ∆Z. Y el circuito modificado es como se muestra en la figura 2. Necesitamos calcular (I’) la corriente que pasa a través del circuito en la figura 2.

Aplicar KVL a la figura 2;

Debido al cambio en la impedancia, el cambio en la corriente del lazo se denota como ∆I. Y el ∆I es igual a la diferencia entre la corriente I antigua y la corriente I nueva.

ΔYo =yo – Yo’

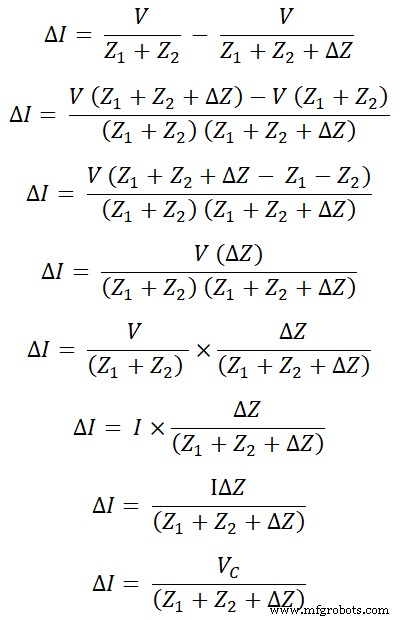
Ahora, considere la siguiente figura.

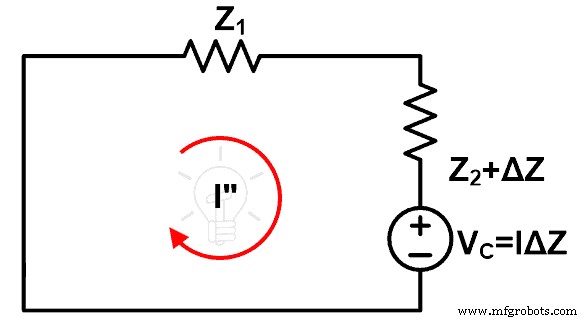
Esta figura representa el circuito después de la implementación del teorema de compensación. Aquí, la fuente de voltaje original se elimina mediante un cortocircuito (suponga que la fuente de voltaje es ideal).

Encontraremos la corriente que pasa por este bucle que es yo”. Y compare esta corriente con la corriente calculada arriba.

Para calcular la corriente que pasa por el bucle, aplique KVL a la figura anterior.

V_C =Z ₁ Yo” +(Z ₂ +ΔZ ) Yo”

V_C =Yo” (Z ₁ + Z ₂ + ΔZ )

Yo” =V_C / (Z ₁ + Z ₂ + ΔZ )

Yo” =Δyo

Por lo tanto, se demuestra que el cambio en la corriente (∆I) después de la modificación es igual a la corriente calculada por el teorema de compensación.

Y hemos probado el enunciado del teorema de compensación.

• Publicación relacionada: Teorema de superposición:análisis de circuito con ejemplo resuelto

Un experimento del teorema de compensación

Objetivo: Demuestre el teorema de compensación y encuentre el cambio en la corriente.

Aparato: Voltímetro, amperímetro, resistencias, cables de conexión, protoboard,

Diagrama de circuito:

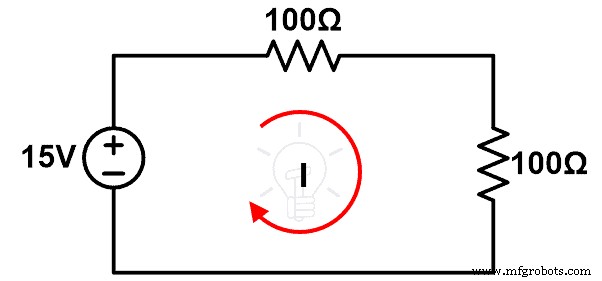
Procedimiento:

Paso 1 Conecte los componentes como se muestra en la figura 5 usando un cable de conexión en una placa de prueba.

Paso-2 Medir la corriente I.

Paso 3 Conecte los componentes como se muestra en la figura 6. Aquí, hemos conectado una resistencia extra.

Paso-4 Mida la corriente I1.

Paso-5 Calcular el cambio en la corriente (∆I) a partir del valor de I e I1.

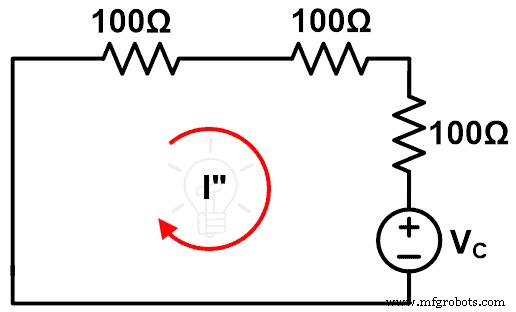
Paso 6 Conecte los componentes como se muestra en la figura 7. Este circuito es un circuito de compensación.

Paso-7 Medir la corriente I”.

Paso 8 Compare el cambio en la corriente (∆I) con la I”.

Tabla de Experimento:

Sr. No.	Yo	Yo 1	∆Yo	Yo”
1

Resultado:

Al comparar el valor de la corriente I’’ con ∆I, podemos probar el teorema de compensación.

• Publicación relacionada: Teorema de Millman:análisis de circuitos de CA y CC:ejemplos

Ejemplo de Teorema de Compensación

Ejemplo-1

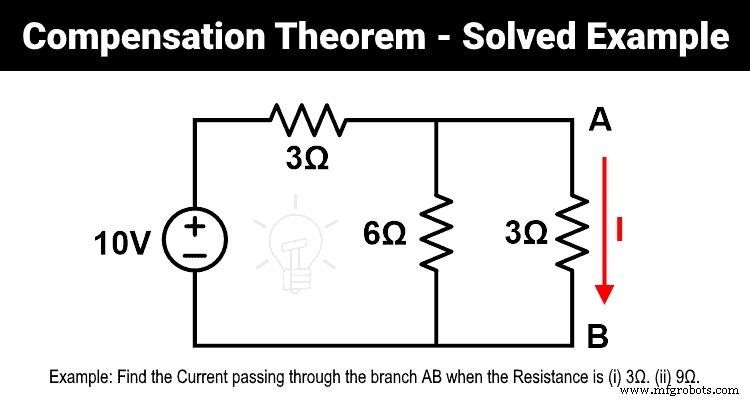
• 1) Encuentra la corriente que pasa por la rama AB cuando la resistencia es 3Ω.
• 2) Encuentra la corriente que pasa a través de la rama AB usando el teorema de compensación cuando la resistencia de 3Ω se cambia a 9Ω.
• 3) Demostrar el teorema de compensación.

Respuesta-1

Como se muestra en la figura, las resistencias de 6Ω y 3Ω están en paralelo. Y esta combinación paralela está conectada en serie con una resistencia de 3Ω. Por lo tanto, la resistencia equivalente será;

R _Ecuación =6 | | 3+3

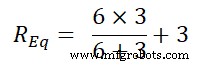
R _Ecuación =2 + 3

R _Ecuación =5 Ω

Según la ley de Ohm;

10 =yo (5)

Yo =10 ÷ 5

Yo =2 A

Ahora, necesitamos encontrar los pasos actuales a través de la rama AB. Entonces, de acuerdo con la regla del divisor actual;

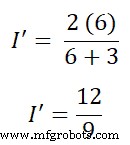
Yo’ =1,333 A (o 3/4 A)

• Publicación relacionada: Teorema de sustitución:guía paso a paso con ejemplo resuelto

Respuesta-2

Necesitamos reemplazar la resistencia de 3Ω con una resistencia de 9Ω. De acuerdo con el teorema de compensación, necesitamos agregar una nueva fuente de voltaje en serie con la resistencia de 9Ω. Y el valor de esta fuente de voltaje es;

V_C =Yo' ΔZ

Dónde,

ΔZ =9 – 3 =6 Ω y I’ =4/3 A (o 1,333 A)

V_C =(4/3A) x 6 Ω

V_C =8 V

Un diagrama de circuito modificado o un diagrama de circuito compensado es como se muestra en la siguiente figura.

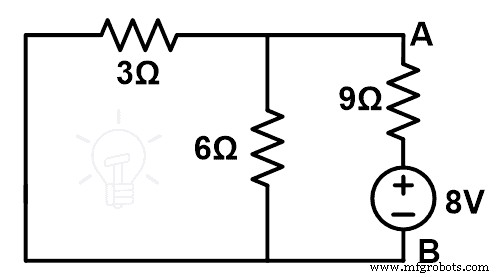
Ahora, encontraremos la resistencia equivalente. Aquí, las resistencias de 3Ω y 6Ω están conectadas en paralelo. Y esta combinación en paralelo está conectada en serie con una resistencia de 9Ω.

R_Eq =3 | | 6 + 9

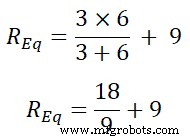
R_Eq =2 + 9

R_Eq =11 Ω

Ahora, según la ley de Ohm;

V =ΔI R

8 =Δyo (11 Ω)

ΔYo =8 ÷ 11

ΔYo =0,7272 A

Entonces, de acuerdo con el teorema de compensación; el cambio en la corriente es 0.7272A.

• Publicación relacionada: Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB

Respuesta-3

Queremos probar el teorema de compensación. Entonces, calculamos la corriente en el ejemplo dado con una resistencia de 9Ω.

El diagrama de circuito modificado se muestra en la siguiente figura.

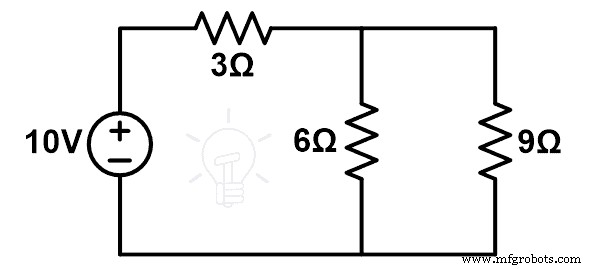
Aquí, las resistencias de 9Ω y 6Ω están conectadas en paralelo y esta combinación en paralelo está conectada en serie con la resistencia de 3Ω.

La resistencia equivalente es igual a;

R_Eq =9 | | 6 + 3

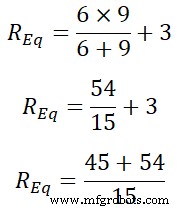
R_Eq =99 ÷ 15

R_Eq =6,66 Ω

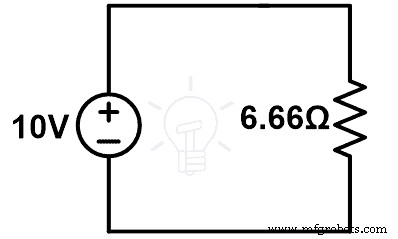
De la figura anterior;

10 =yo (6.66)

Yo =10 ÷ 6,66

Yo =1,5151 A

Según la regla del divisor actual;

Yo” =0,6060A

ΔYo =Yo' – Yo”

ΔYo =(4/3A) – 0,6060

ΔYo =1,333A – 0,6060

ΔYo =0,7273 A

Por lo tanto, se demuestra que el cambio en la corriente calculado a partir del teorema de compensación es el mismo que el cambio en la corriente calculado a partir del circuito original.

• Publicación relacionada:  Teorema de transferencia de potencia máxima para circuitos de CA y CC
  

Ejemplo-2

En el siguiente circuito, encuentre el cambio de corriente si la resistencia de 3Ω se reemplaza por una resistencia de 7Ω usando el teorema de compensación. Y prueba el teorema de compensación.

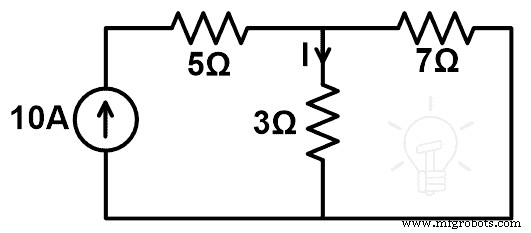
La red anterior se compone únicamente de resistencias y fuentes de corriente independientes. Entonces, podemos aplicar el teorema de compensación a esta red.

En esta figura, la red está alimentada por una fuente de corriente. Ahora, necesitamos encontrar la corriente que pasa a través de la rama de resistencia de 3Ω. Esta corriente se puede encontrar usando KCL o KVL. Pero aquí, esta corriente se puede encontrar fácilmente con la regla del divisor de corriente.

Por lo tanto, de acuerdo con la regla divisoria actual;

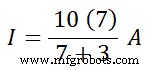
Yo =70 ÷ 10 A

Yo =7 A

En la red original con resistencia de 3Ω, la corriente que pasa por esa rama es de 3A. Ahora, necesitamos cambiar esta resistencia de 3Ω a 7Ω. Debido a esta modificación, se cambiará el paso de corriente por ese ramal. Y encontraremos este cambio de corriente por el teorema de compensación.

Para eso, necesitamos hacer una red de compensación. Para crear una red de compensación, debemos eliminar todas las fuentes independientes disponibles en la red cortocircuitando la fuente de voltaje y abriendo el circuito de la fuente de corriente.

En esta red, solo hay disponible una fuente actual. Suponemos que la fuente de corriente es una fuente de corriente ideal. Por lo tanto, no necesitamos agregar la resistencia interna.

La segunda modificación que debemos hacer en el circuito de compensación es agregar una fuente de voltaje adicional. Y el valor de este voltaje es;

V_C =yo ΔZ

V_C =7 × (7 – 3)

V_C =7 × 4

V_C =28 V

La red de compensación es como se muestra en la figura a continuación.

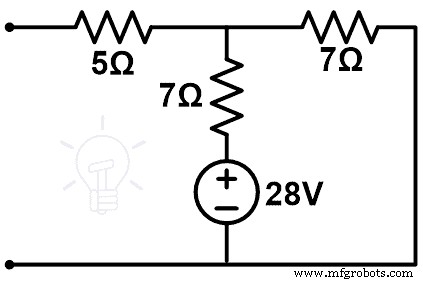
Esta figura tiene un solo bucle. Y la corriente que pasa por la rama de 7Ω nos dará el cambio de corriente (∆I).

ΔYo =V_C ÷ (7+7)

ΔYo =28 ÷ 14

ΔYo =2 A

Para probar el teorema de compensación, encontraremos la corriente en el circuito con una resistencia de 7Ω conectada. El diagrama de circuito modificado se muestra en la siguiente figura.

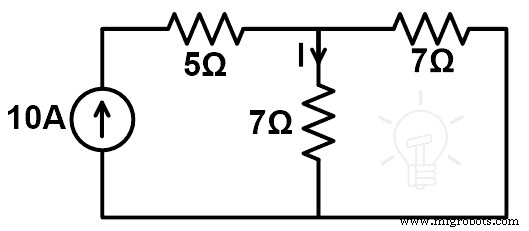
Yo” =(10 (7)) ÷ (7 + 7)

Yo” =70 ÷ 14

Yo” =5 A

Aplicando la regla divisoria actual;

Para encontrar el cambio de corriente, necesitamos restar esta corriente de la corriente que pasa a través de la red original.

ΔYo =yo – Yo”

ΔYo =7 – 5

ΔYo =2 A

Por lo tanto, hemos probado el teorema de compensación.

Tutoriales de análisis de circuitos eléctricos relacionados:

• Análisis del circuito del SUPERNODO:paso a paso con un ejemplo resuelto
• Análisis del circuito SUPERMESH:paso a paso con un ejemplo resuelto
• Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto
• Calculadora de la regla de Cramer:sistema de 2 y 3 ecuaciones para circuitos eléctricos
• Puente de Wheatstone:circuito, trabajo, derivación y aplicaciones
• Calculadoras de ingeniería eléctrica y electrónica
• Más de 5000 fórmulas y ecuaciones de ingeniería eléctrica y electrónica