Mapas de Karnaugh de 4 variables más grandes

Saber cómo generar código Gray debería permitirnos construir mapas más grandes. En realidad, todo lo que tenemos que hacer es mirar la secuencia de izquierda a derecha en la parte superior del mapa de 3 variables y copiarla en el lado izquierdo del mapa de 4 variables. Vea a continuación.

Reducciones de 4 mapas de K variable

Los siguientes mapas de Karnaugh de cuatro variables ilustran la reducción de expresiones booleanas demasiado tediosa para el álgebra booleana. Las reducciones se pueden hacer con álgebra booleana.

Sin embargo, el mapa de Karnaugh es más rápido y más fácil, especialmente si hay muchas reducciones lógicas por hacer.

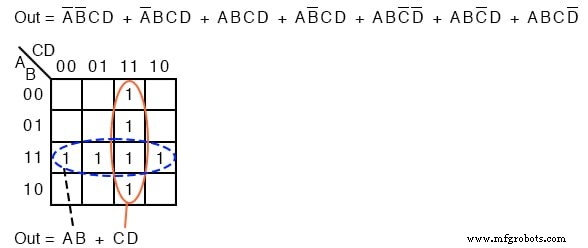
La expresión booleana anterior tiene siete términos de producto. Están mapeados de arriba a abajo y de izquierda a derecha en el mapa K de arriba. Por ejemplo, el primer término P A’B’CD es la primera fila, tercera celda, correspondiente a la ubicación del mapa A =0, B =0, C =1, D =1 .

Los otros términos del producto se colocan de manera similar. Rodeando los grupos más grandes posibles, arriba se muestran dos grupos de cuatro.

El grupo horizontal punteado corresponde al término de producto simplificado AB . El grupo vertical corresponde al CD booleano. Dado que hay dos grupos, habrá dos términos de producto en el resultado de la suma de productos de Fuera =AB + CD .

Dobla las esquinas del mapa de abajo como si fuera una servilleta para que las cuatro celdas estén físicamente adyacentes.

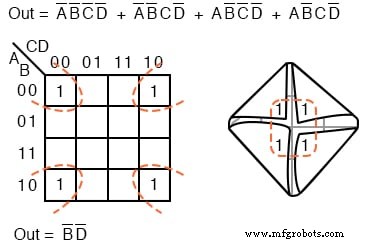
Las cuatro celdas de arriba son un grupo de cuatro porque todas tienen las variables booleanas B ’ y D ’ en común. En otras palabras, B =0 para las cuatro celdas y D =0 para las cuatro celdas.

Las otras variables (A, C) son 0 en algunos casos, 1 en otros casos con respecto a las cuatro celdas de las esquinas.

Por tanto, estas variables (A, C) no están involucrados con este grupo de cuatro. Este único grupo sale del mapa como un término de producto para el resultado simplificado: Out =B’D ’

Para el mapa K a continuación, enrolle los bordes superior e inferior en un cilindro formando ocho celdas adyacentes.

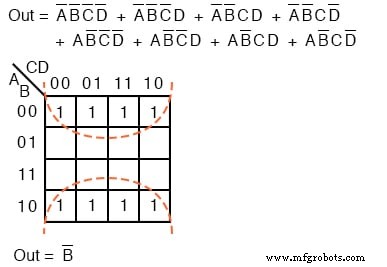
El grupo de ocho anterior tiene una variable booleana en común: B =0 . Por lo tanto, el grupo de ocho está cubierto por un término p: B ’ . La expresión booleana original de ocho términos se simplifica a Out =B ’

Términos P en 4 mapas de variable K

La siguiente expresión booleana tiene nueve términos p, tres de los cuales tienen tres booleanos en lugar de cuatro. La diferencia es que mientras que cuatro términos de producto variable booleanos cubren una celda, los tres términos p booleanos cubren un par de celdas cada uno.

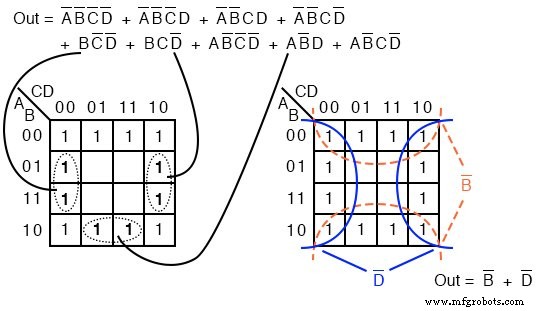
Los seis términos de producto de cuatro variables booleanas se asignan de la manera habitual anteriormente como celdas individuales. Los tres términos de variables booleanas (tres cada uno) se asignan como pares de celdas, como se muestra arriba.

Tenga en cuenta que estamos mapeando términos p en el mapa K, no extrayéndolos en este punto.

Para simplificar, formamos dos grupos de ocho. Las celdas de las esquinas se comparten con ambos grupos. Esto esta bien. De hecho, esto conduce a una mejor solución que formar un grupo de ocho y un grupo de cuatro sin compartir ninguna celda. La solución final es Fuera =B ’+ D’

A continuación, asignamos la expresión booleana no simplificada al mapa de Karnaugh.

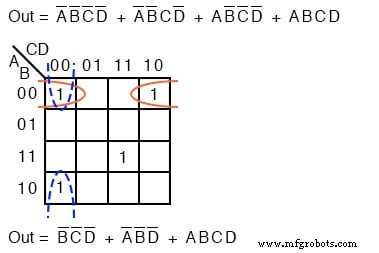
Arriba, tres de las células se forman en grupos de dos células. Una cuarta celda no se puede combinar con nada, lo que ocurre a menudo en los problemas del “mundo real”. En este caso, el término p booleano ABCD no se modifica en el proceso de simplificación. Resultado: Fuera =B’C’D ’+ A ’B ’D’ + ABCD

A menudo, existe más de una solución de costo mínimo para un problema de simplificación. Tal es el caso que se ilustra a continuación.

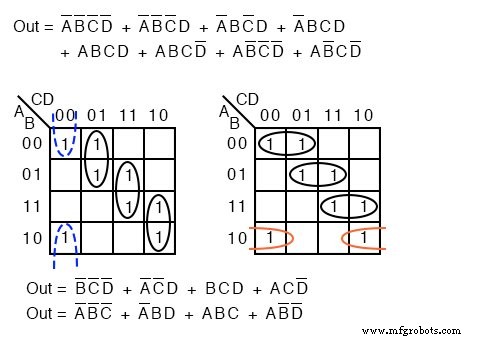
Ambos resultados anteriores tienen cuatro términos de producto de tres variables booleanas cada uno. Ambos son igualmente válidos costo mínimo soluciones. La diferencia en la solución final se debe a cómo se agrupan las celdas como se muestra arriba.

Una solución de costo mínimo es un diseño lógico válido con el número mínimo de puertas con el número mínimo de entradas.

A continuación, mapeamos la ecuación booleana no simplificada como de costumbre y formamos un grupo de cuatro como primer paso de simplificación. Puede que no sea obvio cómo recoger las celdas restantes.

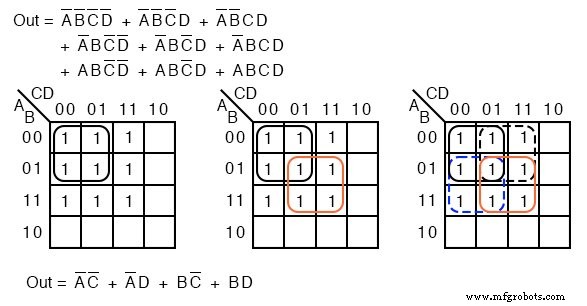
Recoge tres celdas más en un grupo de cuatro, centro arriba. Aún quedan dos celdas. el método de costo mínimo para recogerlos es agruparlos con las celdas vecinas como grupos de cuatro como se muestra arriba a la derecha.

En una nota de advertencia, no intente formar grupos de tres. Las agrupaciones deben ser potencias de 2, es decir, 1, 2, 4, 8 ...

A continuación, tenemos otro ejemplo de dos posibles soluciones de costo mínimo. Comience formando un par de grupos de cuatro después de mapear las celdas.

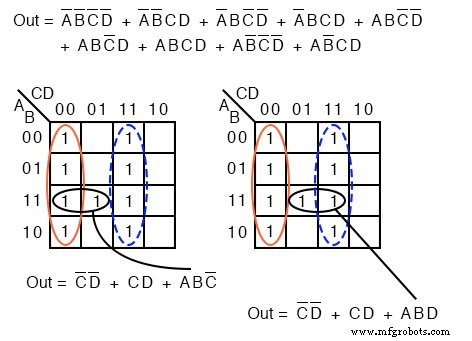
Las dos soluciones dependen de si la única celda restante se agrupa con el primero o el segundo grupo de cuatro como un grupo de dos celdas. Esa celda aparece como ABC ’ o ABD , tu elección.

De cualquier manera, esta celda está cubierta por cualquier término de producto booleano. Los resultados finales se muestran arriba.

A continuación tenemos un ejemplo de una simplificación usando el mapa de Karnaugh a la izquierda o el álgebra booleana a la derecha. Trazar C ’ en el mapa como el área de todas las celdas cubiertas por la dirección C =0 , las 8 celdas a la izquierda del mapa. Luego, grafica el único ABCD celda.

Esa única celda forma un grupo de 2 celdas como se muestra, lo que se simplifica al término P ABD , para un resultado final de Out =C ’+ ABD .

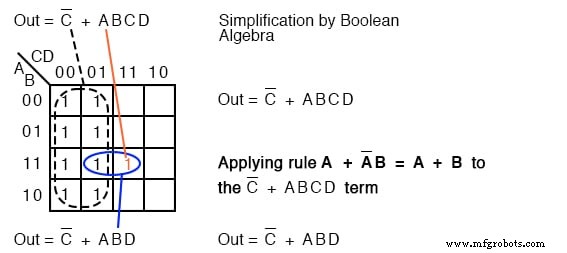
Este (arriba) es un ejemplo poco común de un problema de cuatro variables que se puede reducir con álgebra de Boole sin mucho trabajo, asumiendo que recuerdas los teoremas.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de mapeo de Karnaugh