Mapeo nanomecánico cuantitativo de elastómero de poliolefina a nanoescala con microscopía de fuerza atómica

Materiales y métodos

Materiales

Se adquirió un kit de muestra PeakForce QNM de Bruker Co. (Santa Barbara, CA). En el kit se incluyeron una muestra de mezcla de polímeros, una muestra de zafiro y una muestra de comprobación de la punta. La muestra de mezcla de polímeros está compuesta por una película delgada de poliestireno (PS) mezclado con poliolefina de baja densidad (LDPE). Las muestras se montaron en discos de metal usando cinta de doble cara y se usaron tal como se recibieron. De acuerdo con la fabricación, se fundió por centrifugación una mezcla de PS y LDPE (copolímero de etileno-octeno) sobre un sustrato de silicio, creando una película con diferentes propiedades del material. Las sondas RTESPA-150 se adquirieron de Bruker Co. (Santa Barbara, CA) con una constante de resorte nominal de 5 N / m. La parte trasera de los voladizos de la sonda se recubrió con una fina capa de aluminio para mejorar la deflexión del láser.

Calibraciones

Se utilizó un modo ScanAsyst equipado con Dimension ICON AFM (Bruker Co., Santa Barbara, CA) para realizar calibraciones y mediciones mecánicas. Se realizaron calibraciones sobre la sensibilidad de la deflexión del voladizo, la constante del resorte del voladizo y el radio de la punta para la rampa de fuerza y ​​el volumen de fuerza. En este estudio se utilizaron tres sondas del mismo lote. Los protocolos de calibración fueron los siguientes. La sensibilidad de deflexión en voladizo se calibró realizando una rampa de fuerza a través del llamado enfoque de calibración táctil, en el que se llevó una sonda RTESPA-150 a una superficie muy dura, en este caso la muestra de zafiro. La salida de la rampa se seleccionó para Z. El tamaño de la rampa se mantuvo a 200 nm y el umbral de activación relativo se fijó en 0,3 V por encima del fondo de la línea de base. Después de recopilar una curva de desplazamiento piezoeléctrico de fuerza versus Z, se utilizaron un par de líneas para definir la parte más lineal de la región de contacto. La sensibilidad de deflexión se calibrará y guardará automáticamente una vez que haga clic en Actualizar sensibilidad de deflexión. La sensibilidad de deflexión medida fue 44,7 ± 4,2 nm / V ( n =3). A continuación, se realizó un ajuste térmico para adquirir el espectro de vibración del voladizo en aire libre debido a la energía térmica. El pico de frecuencia de resonancia fue resaltado y ajustado por el software NanoScope en tiempo real proporcionado por el fabricante de AFM (Bruker Co. Santa Barbara, CA). Basado en la teoría del teorema de equipartición,

donde \ (k _ {{\ text {B}}} \) es la constante de Boltzmann, \ (T \) es la temperatura absoluta en Kelvin y \ (d \) es el valor cuadrático medio de la amplitud de vibración en voladizo. La constante de resorte \ (k \) se calculó en consecuencia teniendo en cuenta un factor de corrección de 1.09. El radio de la punta se estimó escaneando con cuidado la sonda a través de la muestra de comprobación de la punta. La muestra está compuesta de titanio que tiene extremos puntiagudos en algunas regiones. Cada extremo afilado capturaría una parte de la forma de la punta. Al final, la imagen de la topografía de muestra podría usarse para reconstruir la forma de la punta, que se presume que es una esfera. Para estimar con precisión el radio de la punta, también se necesitaba una profundidad de sangría. La profundidad de la sangría (18,3 ± 2,6 nm, n =3) se obtuvo midiendo la distancia entre la separación cero y el punto más bajo en el salto en contacto. Por lo tanto, el radio efectivo de la punta se calibró sustituyendo el valor de sangría en la Altura 1 desde el ápice en la imagen de verificación de la punta.

La distancia de sincronización y la sensibilidad de amplitud PFT son exclusivas de la técnica PFQNM. También necesitan ser calibrados. La distancia de sincronización se define como una constante de tiempo en la que el piezo Z alcanza la posición más baja. La sensibilidad de amplitud de PFT se conoce como un factor de escala que transfiere la señal de control de entrada digital al desplazamiento piezoeléctrico Z físico. Su precisión asegura que el piezo Z se mueva como se desee. Tanto la distancia de sincronización como la sensibilidad de amplitud de PFT se calibraron en la muestra de zafiro utilizando un enfoque de calibración táctil. En particular, la distancia de sincronización y la sensibilidad de amplitud de PFT dependen de la frecuencia. Ambos fueron calibrados a frecuencias discretas. En este trabajo, se seleccionó una amplia gama de frecuencias que van desde 0.125k a 2k Hz.

Mapeo nanomecánico cuantitativo PFQNM

Se cargaron sondas RTESPA-150 para el mapeo nanomecánico cuantitativo de la muestra de LDPE. Las constantes de resorte calibradas fueron 3.9 ± 1.4 N / m (n =3). Al escanear, el usuario establece el punto de ajuste de fuerza en 5 nN mientras deja que el control automático de ScanAsyst optimice la tasa de adquisición de imágenes (tasa de escaneo), la ganancia de retroalimentación y el rango Z. El píxel digital se mantuvo en 256 × 256 por imagen. La frecuencia de PFT se varió de 2k a 0.125k Hz entre experimentos para producir carga y descarga de fuerza dependiente del tiempo. Para una amplitud de PFT de 100 nm a una frecuencia de PFT de 2 kHz, la tasa de carga de fuerza correspondiente fue de 0,8 mm s ⁻¹ . Se supuso que la relación de Poisson para el LDPE viscoelástico era de 0,35 [13]. Se escaneó una región de prospección de 5 µm × 5 µm simultáneamente con mediciones topográficas y mecánicas. El controlador NanoScope tenía suficiente ancho de banda para calcular datos mecánicos y mostrarlos en canales de software en tiempo real. Esos datos se guardaron en imágenes sin procesar para su posterior análisis fuera de línea. Por lo tanto, se capturaron varios canales de imagen, incluido el sensor de altura, el módulo DMT, el mapa de adherencia, los canales de indentación y disipación de energía. Una vez identificados los componentes LDPE y poliestireno. Se realizaron mediciones de PFQNM de alta resolución espacial en LDPE en un escaneo de 0,5 µm × 0,5 µm.

Rampa de fuerza AFM y volumen de fuerza rápida

La rampa de fuerza y ​​el volumen de fuerza rápido se lograron aumentando el desplazamiento piezoeléctrico Z mientras se monitoreaba la deflexión vertical del voladizo. El tamaño de la rampa fue de 200 nm. El punto de ajuste de fuerza de disparo bajo a 5 nN se logró mediante un mecanismo de sustracción de fondo constante que excluye la desviación de la desviación durante el proceso de rampa. Se definió una matriz de muestreo de rampa de fuerza sobre una región de 0,5 µm × 0,5 µm. Las velocidades de rampa fueron 0,1 Hz, 1 Hz, 10 Hz, 20 Hz, 61 Hz y 122 Hz. Para una tasa de rampa de 1 Hz y un tamaño de rampa de 200 nm, la tasa de carga de fuerza correspondiente fue de 400 nm s ⁻¹ . Se recopilaron curvas de rampa de 16 × 16 para 0,1 Hz y 1 Hz, mientras que curvas de rampa de 128 × 128 para 10 Hz, 20 Hz, 61 Hz y 122 Hz.

Experimento de fluencia

El escáner Stargate fue calibrado a la deriva para el experimento de fluencia. Las sondas RTESPA-150 se pusieron en contacto con una región de LDPE limpia de la muestra de PS / LDPE hasta que alcanzaron una carga de fuerza preestablecida de 2 nN. La función de controles de superficie del software NanoScope permitió mantener la sonda en la muestra durante cierto período de tiempo, en este caso 5 s. Este período se denominó segmento de espera. La fuerza aplicada se mantuvo constante manteniendo la fuerza del gatillo. Se recopilaron mil veinticuatro puntos de datos para el segmento de espera. Se adquirieron tanto el sensor de altura en función del tiempo como el error de deflexión (fuerza) en función del tiempo. Se capturaron al menos 50 curvas de fluencia en ubicaciones seleccionadas al azar. Se realizaron tres experimentos independientes. Se llevó a cabo un experimento de control en blanco sobre la muestra de zafiro. Como se esperaba, no se observó ningún cambio apreciable en Z.

Configuración experimental

Para trazar cuantitativamente las propiedades mecánicas de la muestra de LDPE (Fig.1), el experimento se diseñó de tal manera que una punta en voladizo afilada se hundió en la muestra de LDPE y se retiró de la superficie de la muestra cuando se logró una carga de fuerza preestablecida ( Figura 1a). La fuerza se registró detectando la señal de deflexión vertical en el fotodiodo sensible a la posición (PSPD). El movimiento en voladizo fue impulsado por el movimiento piezoeléctrico Z. Dependiendo de la elección de la técnica, la señal de excitación podría ser una onda triangular (FV), una onda triangular redondeada en las esquinas (FFV) o una señal de onda sinusoidal (PFQNM). El PFQNM se dibujó esquemáticamente en la Fig. 1b, la curva de fuerza versus tiempo demostró claramente que la punta experimentó un contacto instantáneo cuando se acercó a la superficie de la muestra y un desprendimiento repentino del contacto cuando se alejó de la superficie de la muestra. La Distancia de sincronización definió el punto de inflexión que separaba la curva de aproximación de la curva de retracción. En una superficie dura, este punto era una constante de tiempo cuando el piezo Z alcanzaba la posición más baja. También significaba cuándo la fuerza alcanzó la fuerza máxima. Por el contrario, en una muestra blanda compatible, este punto podría cambiar un poco debido a la deformación de la muestra dependiente del tiempo. Independientemente de las técnicas adoptadas, AFM registró la fuerza frente a la curva de desplazamiento Z y luego se convirtió en la fuerza frente a la curva de separación punta-muestra (Fig. 1c). La parte de contacto de la curva de retracción se ajustó con un modelo DMT linealizado que se describe a continuación y se extrajo el módulo DMT. La disipación de energía se calculó integrando el bucle de histéresis. Se eligió prudentemente un voladizo con una constante de resorte adecuada para que la punta del voladizo pueda sangrar en la muestra pero tenga suficiente sensibilidad a la fuerza. Por otro lado, también se debe considerar el radio de la punta porque la tensión aplicada también depende del área de contacto. A la luz de estos, se seleccionaron las sondas RTESPA-150 porque producen la cantidad correcta de fuerza para sangrar en la muestra pero preservan una alta sensibilidad a la fuerza al mismo tiempo.

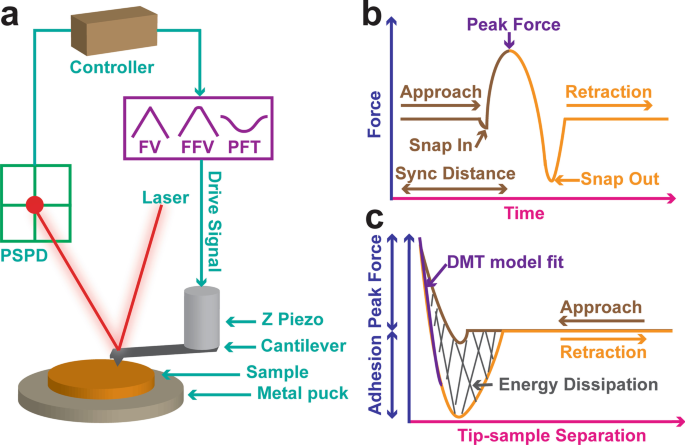
Mecanismo de rampa de fuerza AFM, diseño experimental, adquisición e interpretación de datos. La muestra de LDPE se montó en un disco de metal. Una punta en voladizo afilada se hundió en la muestra de LDPE y se retrajo cuando se alcanzó una fuerza aplicada preestablecida ( a ). Un láser brilló desde la parte superior, golpeó y se desvió desde la parte trasera del voladizo. La señal de desviación fue recibida por un fotodiodo sensible a la posición (PSPD). El movimiento en voladizo fue impulsado por el piezo Z adjunto. Dependiendo de la elección de la técnica, la señal de excitación podría ser una onda triangular (FV), una onda triangular redondeada en las esquinas (FFV) o una onda sinusoidal (PFQNM). La medición de fuerza PFQNM se representó esquemáticamente en b La gráfica de fuerza versus tiempo ilustraba claramente que la punta experimentó un contacto instantáneo cuando se acercó a la superficie de la muestra y un desprendimiento repentino del contacto cuando se alejó de la superficie de la muestra. La distancia de sincronización era una constante de tiempo en la que el sensor de altura alcanzaba la posición más baja. La fuerza frente a la curva de desplazamiento Z (F-Z) fue registrada por el AFM y luego se convirtió en la fuerza frente a la curva de separación punta-muestra (F-D) ( c ). El módulo DMT se extrajo ajustando la parte de contacto de la curva de retracción con el modelo DMT. La integración sobre el bucle de histéresis se denominó disipación de energía

Análisis de datos

El análisis de datos fuera de línea se realizó con el software NanoScope Analysis (Bruker Co., Santa Barbara, CA) suministrado por la fábrica de AFM. Todas las imágenes topográficas se sometieron a un aplanamiento de primer orden que elimina la deriva Z piezoeléctrica, el ruido de fondo y corrige la inclinación de la muestra. La rugosidad de la superficie se evaluó mediante la característica de rugosidad de la superficie proporcionada por el software NanoScope Analysis.

$$ R _ {{\ text {q}}} =\ sqrt {\ frac {{\ sum \ left ({Z _ {{\ text {i}}} - Z _ {{\ text {m}}}} \ right ) ^ {2}}} {N}} $$ (2)

donde \ (N \) es el número total de puntos dentro del área de la imagen, \ (Z _ {{\ text {i}}} \) es la \ (Z \) altura de la i th punto de datos, y \ (Z _ {{\ text {m}}} \) es la altura \ (Z \) media en toda el área. Todas las imágenes de datos mecánicos se dejaron intactas sin nivelar.

Tanto la rampa de fuerza, el volumen de fuerza rápida como el PFQNM produjeron curvas de fuerza versus desplazamiento piezoeléctrico Z (F-Z). Las curvas de fuerza versus separación punta-muestra (F-D) son más significativas físicamente y más demandadas para el ajuste del modelo. El desplazamiento Z consta de tres componentes, a saber, separación punta-muestra ( D ), deflexión en voladizo ( d ) y profundidad de sangría (\ (\ delta \)). La conversión de F-Z a F-D requiere restar la deflexión del voladizo ( d ) y profundidad de sangría (\ (\ delta \)) a partir del desplazamiento Z. Puede realizarse en un software de control en tiempo real o mediante un software de análisis de datos fuera de línea, siempre que se hayan calibrado la sensibilidad de deflexión del voladizo y la constante del resorte. Además, se ejecutó la función de corrección de la línea de base para compensar la línea de base de la curva de fuerza a cero. Finalmente, se obtuvieron las curvas F-D y se sometieron al ajuste del modelo DMT. Según la teoría del contacto de Hertz,

$$ F _ {{{\ text {appl}}}} =\ frac {4} {3} E_ {r} \ sqrt R \ delta ^ {{\ frac {3} {2}}} + F _ {{{ \ text {adh}}}} $$ (3)

donde \ (F _ {{{\ text {appl}}}} \) es la fuerza que la punta aplicó sobre la muestra. Se tiene en cuenta la fuerza de adherencia (\ (F _ {{{\ text {adh}}}} \)). \ (R \) es el radio de la punta de la supuesta punta de la esfera. \ (\ delta \) es la profundidad de la sangría. \ (E _ {{\ text {r}}} \) es el módulo de Young reducido. Está relacionado con los módulos de tip y sample,

$$ \ frac {1} {{E _ {{\ text {r}}}}} =\ left ({\ frac {{1 - v _ {{\ text {s}}} ^ {2}}} {{ E _ {{\ text {s}}}}}} \ right) + \ left ({\ frac {{1 - v _ {{\ text {t}}} ^ {2}}} {{E _ {{\ text {t}}}}}} \ derecha) $$ (4)

donde \ (v _ {{\ text {s}}} \) y \ (v _ {{\ text {t}}} \) son las proporciones de Poisson de la muestra y la punta de AFM, respectivamente. \ (E _ {{\ text {s}}} \) y \ (E _ {{\ text {t}}} \) son los módulos de muestra de Young y la punta de AFM, respectivamente. El módulo de Young de la punta es varios órdenes de magnitud mayor que el de la muestra de LDPE, por lo que el término de la punta puede despreciarse. Una vez que se conocen \ (E _ {{\ text {r}}} \) y \ (v _ {{\ text {s}}} \), \ (E _ {{\ text {s}}} \) se puede calculado.

Tomando ambos lados de la Ec. (3) a la potencia \ (\ frac {2} {3} \) después de restar la \ (F _ {{{\ text {adh}}}} \) de \ (F _ {{{\ text {appl}} }} \), se ha empleado un modelo linealizado para ajustar todos los datos de fuerza [30]. Este modelo no requiere identificación del punto de contacto.

$$ \ left ({F _ {{{\ text {appl}}}} - F _ {{{\ text {adh}}}}} \ right) ^ {{\ frac {2} {3}}} =\ izquierda ({\ frac {4} {3} E _ {{\ text {r}}} \ sqrt R} \ right) ^ {{\ frac {2} {3}}} \ delta $$ (5)

Entonces \ (E _ {{\ text {r}}} \) y \ (E _ {{\ text {s}}} \) se extrajeron como resultado.

$$ E _ {{\ text {r}}} =\ frac {3} {4} \ left ({\ frac {{\ left ({F _ {{{\ text {appl}}}} - F _ {{{ \ text {adh}}}}} \ right) ^ {{\ frac {2} {3}}}}} {\ delta}} \ right) ^ {{\ frac {3} {2}}} \ frac {1} {{\ sqrt R}} =\ frac {3} {4} \; {\ text {pendiente}} ^ {{\ frac {3} {2}}} \ frac {1} {{\ sqrt R}} $$ (6)

La fuerza aplicada se calculó a partir de la ley de Hooke, ya que el voladizo actuaba como un resorte.

$$ F _ {{{\ text {appl}}}} =k \ times d $$ (7)

donde \ (k \) es la constante del resorte en voladizo y \ (d \) es la desviación del voladizo, que se calculó multiplicando la sensibilidad de la desviación del voladizo por la señal de desviación vertical.

Para el análisis de cumplimiento de fluencia, se adoptó la versión Voigt del modelo SLS [19]. En este modelo de tres elementos, un resorte ( E ₁ ) está en serie con un resorte ( E ₂ ) -dashpot Voigt elemento en paralelo. La distancia de compresión ( d ) en función del tiempo se puede describir como:

$$ d (t) =\ frac {F} {{k_ {1}}} + \ frac {F} {{k_ {2}}} \ times \ left ({1 - {\ text {e}} ^ {{- \ frac {{tk_ {2}}} {\ eta}}}} \ derecha) $$ (8)

donde F es la fuerza de carga total, k ₁ y k ₂ son la elasticidad de E ₁ y E ₂ , respectivamente. η representa la viscosidad del amortiguador. Dado que el área de interacción punta-muestra es un área finita, no un solo punto. El modelo se puede mejorar reescribiendo la ecuación en términos de tensión, deformación y módulo. En este estudio se adoptó el método desarrollado por Lam y colaboradores. Su ecuación análoga es:

$$ \ varepsilon (t) =\ frac {\ sigma} {{E_ {1}}} + \ frac {\ sigma} {{E_ {2}}} \ times \ left ({1 - {\ text {e }} ^ {{- \ frac {{tE_ {2}}} {\ eta}}}} \ derecha) $$ (9)

donde ε ( t ) denota deformación como una función del tiempo, σ es el estrés. E ₁ y E ₂ son los módulos elásticos instantáneos y retardados, respectivamente. η representa la viscosidad del amortiguador. Además, el estrés σ y colar ε están relacionados con el módulo E o cumplimiento D por la siguiente relación.

$$ E =\ frac {\ sigma} {\ varepsilon} =\ frac {1} {D} $$ (10)

Por lo tanto, la ecuación (9) se puede reescribir como:

$$ D =\ frac {1} {E} =\ frac {1} {{E_ {1}}} + \ frac {1} {{E_ {2}}} \ veces \ left ({1 - {\ texto {e}} ^ {{- \ frac {{tE_ {2}}} {\ eta}}}} \ derecha) $$ (11)

donde D y E denotan la elasticidad de fluencia y el módulo elástico combinado del sistema, respectivamente. Vuelva a escribir la ecuación. (5) como

$$ \ delta =\ left ({\ frac {{3 \ left ({F _ {{{\ text {appl}}}} - F _ {{{\ text {adh}}}}} \ right)}} { {4 \ sqrt R E _ {{\ text {r}}}}}} \ right) ^ {{\ frac {2} {3}}} $$ (12)

Sustituyendo la ecuación. (11) en la ecuación. (12) da lugar a

$$ \ delta \ left (t \ right) =\ left \ {{\ frac {{3 \ left ({F _ {{{\ text {appl}}}} - F _ {{{\ text {adh}}} }} \ right)}} {{4 \ sqrt R}} \ times \ left ({\ frac {1} {{E_ {1}}} + \ frac {1} {{E_ {2}}} \ times \ left ({1 - {\ text {e}} ^ {{- \ frac {{tE_ {2}}} {\ eta}}}} \ right)} \ right)} \ right \} ^ {{\ frac {2} {3}}} $$ (13)

Los datos de fluencia se pueden ajustar con Eq. (13) y el tiempo de retardo τ se puede derivar usando

$$ \ tau =\ frac {\ eta} {{E_ {2}}} $$ (14)

El tiempo de retardo se conoce como el momento en el que se ha producido ~ 63% de la fluencia.

Todas las mediciones de fuerza se repitieron tres veces. Los resultados se informaron en forma de media ± DE (desviación estándar), mientras que el número de experimentos independientes se denotó como n =3.

Resultados

Para evaluar la efectividad y precisión de PFQNM, se realizó una exploración de encuesta grande con 5 µm × 5 µm. En la Fig. 2 se ensamblaron imágenes PFQNM representativas de una muestra de mezcla de PS / LDPE a 2 kHz. Las Figuras 2a – d eran la imagen del sensor de altura, el canal de módulo DMT, el canal de indentación y el canal de disipación de energía. La región plana fue el componente PS mientras que la región abultada fue el LDPE (Fig. 2a). Una vez finalizada la exploración del levantamiento, se le indicó al AFM que hiciera un acercamiento físico en la región de LDPE y tomara una exploración de tamaño pequeño de alta resolución (1,3 µm × 1,3 µm). Los canales de imagen correspondientes se muestran en la Fig. 2e – h.

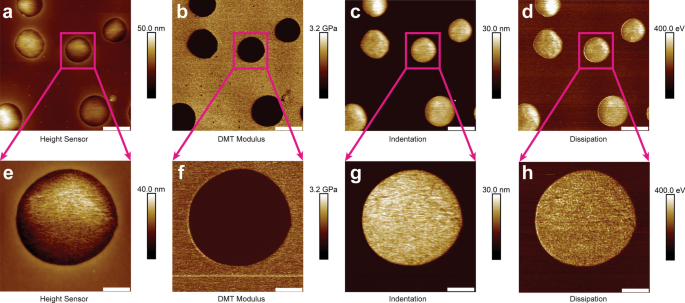
Mapeo nanomecánico PFQNM representativo (5 µm × 5 µm) de muestra de mezcla de PS / LDPE a 2 kHz. Paneles a - d son la imagen del sensor de altura, el canal de módulo DMT, el canal de indentación y el canal de disipación de energía. Para imágenes a - d , las barras de escala representan 1 µm. Una vez finalizado el escaneo del levantamiento, se guía al AFM para que haga un acercamiento físico en la región de LDPE y tome un escaneo de tamaño pequeño de alta resolución (1.3 µm × 1.3 µm). Los canales de imagen correspondientes se muestran en los paneles e – h . La barra de escala representa 260 nm para paneles e - h

A continuación, se llevaron a cabo PFQNM, FV y FFV sobre una región de LDPE pura a 0,5 µm x 0,5 µm. En la Fig. 3a-d se recogió un conjunto representativo de PFQNM a 2 kHz. Incluían sensor de altura, mapeo de módulo, disipación de energía e indentación. La rugosidad de la superficie de la imagen del sensor de altura se informó en forma de \ (R _ {{\ text {q}}} \) como 2,58 ± 0,35 nm. Otro conjunto representativo de FFV a 122 Hz se muestra en la Fig. 3e, f. Tenga en cuenta que no hubo canales de disipación de energía ni de indentación para FV y FFV. Los módulos elásticos a diferentes frecuencias se combinaron (Fig. 3g). Los datos de los módulos de Young se informaron en la Tabla 1. Los módulos de Young a 0.1 Hz, 1 Hz, 10 Hz, 20 Hz, 61 Hz, 122 Hz, 125 Hz, 250 Hz, 500 Hz, 1 k Hz y 2 k Hz fueron 11,7 ± 5,2 MPa ( n =3), 18,2 ± 5,6 MPa ( n =3), 25,4 ± 6,8 MPa ( n =3), 29,6 ± 8,4 MPa ( n =3), 33,8 ± 9,7 MPa ( n =3), 35,7 ± 10,5 MPa ( n =3), 43,8 ± 10,7 MPa ( n =3), 54,8 ± 11,9 MPa ( n =3), 66,7 ± 13,6 MPa ( n =3), 80,9 ± 14,2 MPa ( n =3), 89,6 ± 17,3 MPa ( n =3), respectivamente. El gráfico de dispersión se generó con el software Origin 8.5. Los datos se ajustaron con una función de potencia producida \ (E =15.31 \ times f ^ {{0.23}} \) (\ (R ^ {2} \) =0.96). La relación entre la disipación de energía y las diferentes frecuencias de mapeo se representó en la Fig. 3h. Los valores de disipación de energía obtenidos a 2 kHz, 1 kHz, 0,5 kHz, 0,25 kHz y 0,125 kHz fueron 173,2 ± 21,9 eV ( n =3), 213,8 ​​± 32,7 eV ( n =3), 233,9 ± 29,3 eV ( n =3), 261,1 ± 33,5 eV ( n =3), 293,2 ± 35,6 eV ( n =3), respectivamente. Los datos se ajustaron con una función de potencia que arrojó \ (E _ {{{\ text {diss}}}} =202.83 \ times f ^ {{- 0.18}} ~ \) (\ (R ^ {2} \) =0.97 ). Una curva F-D representativa mostró dos roturas distintas de la punta del AFM de la superficie de la muestra de LDPE (Fig. 3i). La ocurrencia de múltiples rupturas tuvo lugar con mayor frecuencia a frecuencias más bajas, es decir, 0,1-1 Hz.

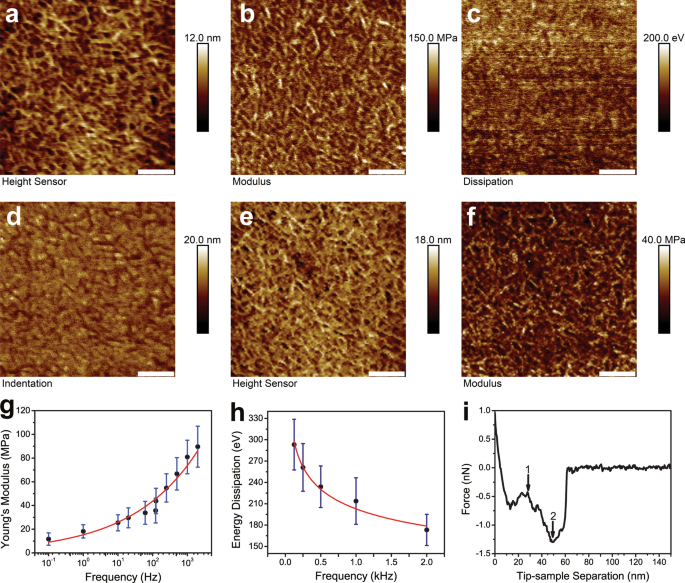
Propiedad mecánica de la muestra de LDPE mapeada a diferentes frecuencias. Paneles a - d fueron la imagen del sensor de altura, el canal de módulo DMT, la disipación de energía y el canal de indentación capturados con PFQNM a 2 kHz en una región de LDPE ordenada. La rugosidad de la superficie de la imagen del sensor de altura se informó en forma de \ (R _ {{\ text {q}}} \) como 2,58 ± 0,35 nm. Los paneles eyf fueron la imagen del sensor de altura y el canal de módulo DMT capturados con FFV a 122 Hz en la región de LDPE limpia. Para imágenes a - f , las barras de escala representaron 100 nm. Relación entre el módulo de Young medido ( E ) y la frecuencia del mapeo de fuerzas ( f ) se representó en g . Los módulos de Young medidos a diferentes frecuencias se tabularon en la Tabla 1. Los datos se ajustaron con una función de potencia producida \ (E =15.31 \ times f ^ {{0.23}} \) (\ (R ^ {2} \) =0.96 ). La relación entre la disipación de energía ( E _diss ) y diferentes frecuencias de mapeo ( f ) se mostró en el panel h . The energy dissipation values obtained at 2 kHz, 1 kHz, 0.5 kHz, 0.25 kHz and 0.125 kHz were 173.2 ± 21.9 eV, 213.8 ± 32.7 eV, 233.9 ± 29.3 eV, 261.1 ± 33.5 eV, 293.2 ± 35.6 eV, respectively. The data were fitted with a power function yielded \(E_{{{\text{diss}}}} =202.83 \times f^{{ - 0.18}} ~\) (\(R^{2}\) = 0.97). A representative F-D curve showed two distinct ruptures of AFM tip from LDPE sample surface (panel i ). The occurrence of multiple ruptures took place more frequently at lower frequencies, i.e. 0.1–1 Hz

Lastly, creep compliance measurement was carried on a neat LDPE region of the PS/LDPE sample. The working principle of AFM creep experiment was illustrated in Fig. 4a. Initially, the AFM tip was brought into contact with sample surface until the predefined force setpoint was reached. The tip was sthen held onto the sample for a certain time period, during which the force was kept constant. Following that, the tip was retracted. In the hold segment, the AFM recorded the change in Z motion. The change in indentation depth as a function of time (Fig. 4b) could be fitted with Voigt version of SLS model using Eq. (13). A representative creep curve was shown in Fig. 4c. The black curve was the data while the red solid line was the fitting curve. The inset indicated the Voigt version of SLS model, featuring a spring (E ₁ ) in series with a spring (E ₂ )-dashpot (η ) Voigt element in parallel. The experiment showed that instantaneous elastic modulus E ₁ , delayed elastic modulus E ₂ , viscosity η , retardation time τ were 22.3 ± 3.5 MPa, 43.3 ± 4.8 MPa, 38.7 ± 5.6 MPa‧s and 0.89 ± 0.22 s, respectively. The data were tabulated in Table 2.

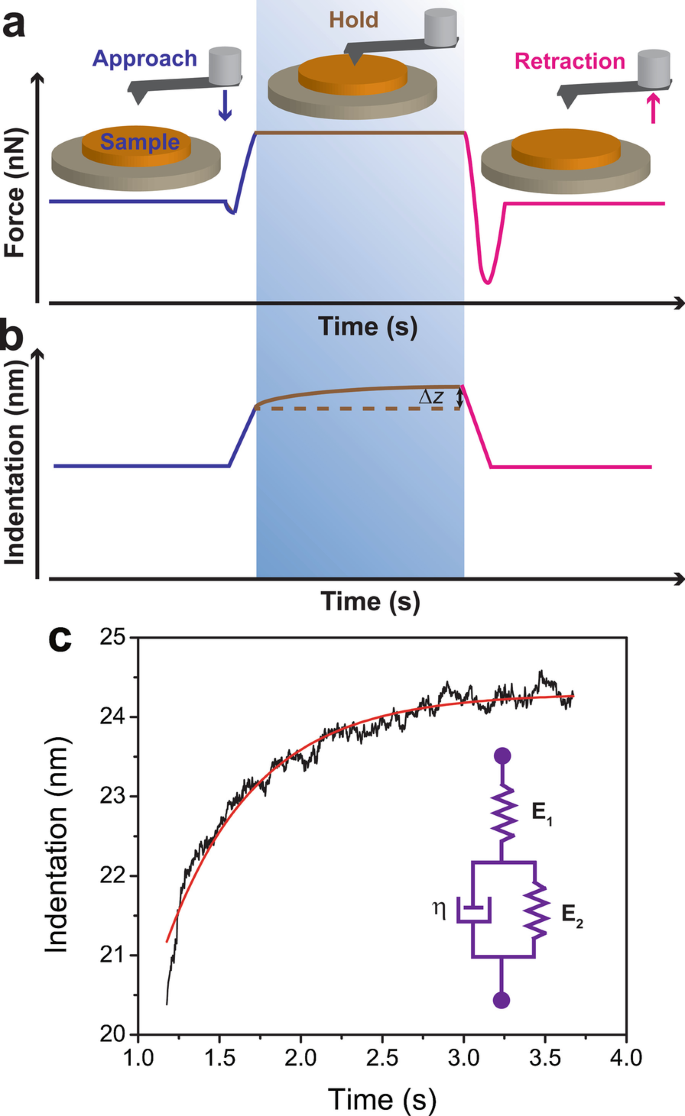
Creep compliance measurement on a neat LDPE region of the PS/LDPE sample. The working principle of AFM creep experiment was illustrated in panel a . Initially, the AFM tip was brought into contact with sample surface till it reached the predefined force setpoint. The tip was then held onto the sample for a certain time period, during which the force was kept constant. Following that, the tip was retracted. In the hold segment, the AFM recorded the change in Z motion (panel b ). The change in indentation depth as a function of time could be fitted with Voigt version of SLS model using Eq. (13). A representative creep curve was shown in panel c . The black curve was the data, while the red solid line was the fitting curve. The inset indicated the Voigt version of SLS model, featuring a spring (E ₁ ) in series with a spring (E ₂ )-dashpot (η ) Voigt element in parallel

Discussion

In the present study, a comprehensive powerful nanomechanical mapping approach for polymer samples has been developed by incorporating a number of nanoscale AFM based force measurements. The approach allows simultaneous high-resolution topography imaging and quantitative nanomechanical mapping. Local mechanical behavior can be correlated with sample topography. More importantly, the time dependent mechanical response of soft viscoelastic materials has been successfully mapped out. The Hertz model is a widely received contact mechanics model [31], in which the scenario when a rigid probe indents a semi-infinite, isotropic, homogeneous elastic surface is described. However, the Hertz model assumes no surface forces, which is not true for soft materials. To overcome this shortcoming, the Johnson–Kendall–Roberts (JKR) model and the DMT model have been developed. Given the setup in this study, the DMT model can be implemented as there are high elastic modulus, low adhesion, and small tip radius involved where long rang surface forces exist. The force setpoint at 5 nN has been empirically obtained, and justified to be the optimum value in terms of getting meaningful indentation depth while the DMT model still holds. Low force load also gives rise to sample deformation in elastic regime not plastic regime. In addition, sharp tip enables high resolution sample topography imaging in PFQNM measurements, which is an attractive advantage when correlates sample topography with mechanical properties.

Tip radius estimation is not trivial in quantitative mechanical measurements. Many researches estimate the tip radius by backward calculation using a sample with known modulus [29, 32]. This work adopts a different reconstruction strategy that does not require such a sample. It has been documented that using blunt tips tend to yield tighter modulus numbers and that sharp tips may overestimate the modulus. However, sharp tips preserve high spatial resolution, an advantage not possessed by other techniques. Polymer fibrils are clearly seen (see a 0.5 µm × 0.5 µm scan in Fig. 3). Sharp tips, even under small load, can penetrate into compliant samples due to large stress, resulting in large indentation. Therefore, it could compromise the validity of the DMT model. That is not the case in this study as the applied force is controlled in a precise and sensitive manner, evidenced by the resulted indentation depth and the effective tip radius in the same order of magnitude (22.5 ± 3.2 nm, n  = 3). Surface roughness (\(R_{{\text{q}}}\)) of the LDPE height image is 2.58 ± 0.35 nm, indicating the surface is flat and surface roughness should not be treated as a confounding factor to quantitative measurements [33]. In addition, the linearized DMT model fit does not require determination of the contact point that could otherwise lead to major errors in the final calculated modulus [34]. Taken together, the current experiment setup fulfills the DMT model.

To evaluate the effectiveness of PFQNM, the PS/LDPE sample has been scanned at large size. The survey scan shows LDPE has higher adhesion than PS (Fig. 2b), suggesting LDPE is stickier. AFM tip indents deeper in LDPE than in PS (Fig. 2c), indicating LDPE is softer than PE. The determined Young’s moduli for LDPE and PS are about 90 MPa and 2.5 GPa, respectively. The PS region is a little stiff for RTESPA-150 probe to indent, thus the measured modulus tends to be higher than the nominal value. Both PFQNM and FFV generate high resolution topography and modulus images (c.f. Fig. 3a, b, e, f). It is noteworthy that FFV requires reasonable data acquisition time, although it is not as impressive as PFQNM but much faster than traditional force ramp. Energy dissipation is an observable that explicitly demonstrates how much energy loss per tapping cycle (Fig. 3h). The more viscoelastic of the material, the more energy loss it incurs. The energy dissipation map demonstrates that AFM probe loses more energy on LDPE than on PS, implying LDPE is viscoelastic and response time plays an important role. The relaxation function for the power-law rheology model is described as \(\varphi =E_{{\text{a}}} \left( {\frac{t}{{t_{0} }}} \right)^{{ - \gamma }}\) [35], where E _a is the apparent Young’s modulus at time t ₀ , is the power-law exponent γ and t ₀ is a timescale factor which is set to 1 s. The dimensionless number γ characterizes the viscoelastic behavior of the material, with γ  = 0 for purely elastic solid and γ  = 1 for purely Newtonian fluid [36]. Current study indicates LDPE has more elastic behavior than viscous counterpart. Figure 3i exhibits an interesting finding in FV experiments that a force curve harboring two rupture events. The multiple rupture events occur more frequently in lower frequencies, i.e. 0.1–1 Hz. It is conceivable that with lower frequency, the tip dwells longer on sample surface that results in forming stronger bonds. When tip is retracted, the slower motion of tip would break the bonds at lower speed, providing the chance of being captured by AFM [37]. On the contrary, when performed at higher frequencies, weaker bonds are formed due to short dwell period and AFM is not capable of capturing transition rupture events due to poor temporal resolution. Another plausible explanation is that the combination of force exerted and longer interaction time on sample induces polymer chain conformation change, as reported previously that force induces rotation of carbon–carbon double bonds [38]. With piconewton force sensitivity and sub-nanometer distance accuracy, F-D curves not only reveal the strength of the formed bonds but also shed insights into the elastic properties and conformational changes. It was documented that at low forces (< 100 pN) and large forces (> 300 pN) the mechanical behavior of polymer chains is majorly affected by its entropic elasticity and enthalpic elasticity, respectively [39].

To further investigate the time dependent mechanical response of LDPE, creep compliance experiment has been carried out on the premise that the closed-loop scanner has been drift calibrated. Experimental data show that instantaneous elastic modulus E ₁ , delayed elastic modulus E ₂ , viscosity η , retardation time τ are 22.3 ± 3.5 MPa, 43.3 ± 4.8 MPa, 38.7 ± 5.6 MPa s and 0.89 ± 0.22 s, respectively (Table 2). This set of values for creep behavior is close to those reported for polyurethane nanocomposites [40] and syndiotactic polypropylene [41] and higher than those for bacterial biofilm [19] and live cells [36, 42]. While large AFM indenter platform measures elastic modulus of soft samples in an ensemble way, it does not enjoy high spatial resolution of elasticity. Such local mechanical properties are critical for some specimen. For instance, cell membranes are composed of various substructures like cytoskeleton, filament network and microvilli, each has varying elasticities [30]. A recent paper has studied the elastic modulus of fibroblast cells in the frequency range of 0.3–250 Hz [43]. The authors have discovered raised apparent Young’s modulus when ramp frequency increased, consistent with the observations of current study. The approaches reported here are as reliable as any other nanomechanical techniques provided the force-indentation has been prudently designed and the data analysis has been carefully executed. The PFQNM measurement is particularly helpful due to its localized correlation of sample topography with mechanical behavior. It is advantageous in terms of local non-destructive probing of mechanical properties over traditional instrumented indentation, where large probe tip is used and large destructive force is applied. Furthermore, the AFM creep experiment provides dynamic mechanical behavior at nanoscale. The methodology presented here offers multiparametric, multifunctional probing of mechanical measurement along with exceptional high spatial resolution. It has been successfully exploited for quantitative nanomechanical mapping of soft polymers such as LDPE, and can potentially be extended to complex biological systems [43,44,45].

Conclusions

Utilizing state-of-the-art PFQNM as well as with FV and FFV, the power-low rheology of a LDPE sample has been evaluated in a time-dependent fashion. Specifically, rigorous calibrations are done. Force data are fitted with a linearized DMT contact mechanics model considering surface adhesion force. Elastic Young’s modulus was measured at frequencies spanned four orders of magnitude. Increased Young’s modulus was discovered with increasing acquisition frequency. The Young’s modulus is 11.7 ± 5.2 MPa at 0.1 Hz but increases to 89.6 ± 17.3 MPa at 2 kHz. The acquisition frequency dependent modulus change could be described by a power function \(E =15.31 \times f^{{0.23}}\) (\(R^{2}\) = 0.96). Energy dissipation in the range of 0.125–2 kHz further supports this observation. Furthermore, creep compliance experiment shows that instantaneous elastic modulus E ₁ , delayed elastic modulus E ₂ , viscosity η , retardation time τ are 22.3 ± 3.5 MPa, 43.3 ± 4.8 MPa, 38.7 ± 5.6 MPa‧s and 0.89 ± 0.22 s, respectively. The multiparametric, multifunctional local probing of mechanical measurement along with exceptional high spatial resolution imaging open new opportunities for quantitative nanomechanical mapping of soft polymers, and can potentially be extended to biological systems.

Disponibilidad de datos y materiales

The datasets used or analyzed during the current study are available from the corresponding author on reasonable request.

Abreviaturas

AFM:

Microscopía de fuerza atómica

DMT:

Derjaguin–Muller–Toporov

FFV:

Fast force volume

FV:

Force volume

JKR:

Johnson–Kendall–Roberts

LDPE:

Low density polyolefin

PFQNM:

PeakForce quantitative nanomechanical mapping

PFT:

PeakForce tapping

PD:

Poliestireno

Un circuito de detección temprana para la mejora de la resistencia de la matriz de memoria de acceso aleatorio resistivo de contacto rellenado Detector de amplio rango de efecto de carga inducido por plasma para procesos CMOS BEOL avanzados