Alta absorción de fotones de fotodetectores infrarrojos de puntos cuánticos lograda por el efecto plasmón de superficie de la matriz de nanoagujeros de metal

Resumen

Con la creciente demanda de dispositivos fotodetectores a pequeña escala, los fotodetectores infrarrojos basados en puntos cuánticos han atraído cada vez más atención en las últimas décadas. En este trabajo, se introducen estructuras periódicas de matriz de nanoagujeros de metal en los fotodetectores infrarrojos de puntos cuánticos para mejorar el rendimiento de la absortividad de fotones a través del efecto de mejora del plasmón de superficie para superar el cuello de botella de la baja eficiencia de absorción óptica que existe en los fotodetectores convencionales. Los resultados demuestran que las estructuras de matriz de nanoagujeros de metal optimizadas pueden mejorar en gran medida la absortividad de fotones hasta un 86,47% en los fotodetectores específicos, que es 1,89 veces mayor que la de los fotodetectores convencionales sin las estructuras de matriz de metal. La gran mejora de la absortividad se puede atribuir al efecto de plasmón de superficie de acoplamiento local causado por las estructuras metálicas de la matriz de nanoagujeros. Se cree que el estudio puede proporcionar cierta orientación teórica para los fotodetectores infrarrojos basados en puntos cuánticos a nanoescala de alto rendimiento.

Antecedentes

Los fotodetectores infrarrojos semiconductores se pueden utilizar para detectar la luz infrarroja y tienen una gran aplicación prometedora en los campos de la investigación científica, la imagen digital, la comunicación óptica y las áreas militares. Hasta la fecha, los fotodetectores de infrarrojos de puntos cuánticos (QDIP) han atraído una atención cada vez mayor en los últimos años debido a sus excelentes propiedades de respuesta a la luz y sus tendencias hacia la miniaturización de dispositivos [1, 2, 3]. Aunque décadas de esfuerzos sostenidos, los científicos han logrado grandes avances en el desarrollo de tecnologías para obtener QDIP de alto rendimiento, aún es necesario realizar más mejoras para enfrentar los desafíos de la miniaturización de dispositivos [4] y las demandas prácticas. Se señala que el acoplamiento de rejillas metálicas en la región activa basada en puntos cuánticos podría considerarse un enfoque eficaz para mejorar el rendimiento de los QDIP [5, 6], que pueden producir un alto coeficiente de fotoabsorción mediante el fotoacoplamiento local de plasmones mejorados efecto.

Según los informes, hay dos tipos principales de estructuras de rejilla metálica que se utilizan para mejorar el rendimiento de los QDIP. Una es la estructura de matriz de orificios de metal y la otra es la estructura de matriz de metal sin orificios. Más concretamente, en la aplicación con respecto a la estructura de la matriz de agujeros metálicos, el grupo de Chang combinó la matriz periódica de agujeros metálicos con la capa de puntos cuánticos en el QDIP en 2007, lo que condujo a la transmisión de luz supernormal del fotodetector [7]. En 2009, Lee et al. propuso un método para QDIP de alta detectividad mediante la integración de cristales fotónicos metálicos con un período de 3.6 μm de matriz de orificios (espesor de 100 nm) [8]. Los resultados de la investigación demuestran que el método puede realizar la respuesta máxima del fotodetector a la longitud de onda de 11,3 μm y producir una detección hasta 30 veces mayor que sin el cristal fotónico metálico. Luego, discutieron el desempeño de la dependencia QDIP de la luz incidente y su aplicación en la matriz del plano focal [9, 10]. También se puede encontrar una mejora de rendimiento similar en los informes mediante el uso de la rejilla de acoplamiento de matriz de metal de orificios [11,12,13,14]. También se proponen estructuras de matriz de metal sin orificios. En 2011, Huang y sus compañeros de trabajo utilizaron la capa de nanopartículas de plata plasmón autoorganizada para mejorar la amplia respuesta espectral del QDIP y obtuvieron una mejora de 2,4 a 3,3 veces [15]. En 2014, el grupo de Chen informó que el rendimiento del fotodetector puede mejorarse mediante el efecto de campo cercano de las nanopartículas de Au [16]. En 2015, el grupo de Ding y el grupo de Wang propusieron las estructuras de acoplamiento de la guía de ondas y la cavidad resonante única del reflector de Praga distribuido [17, 18], respectivamente. Además de las estructuras mencionadas, también se discutieron y analizaron otras estructuras metálicas, por ejemplo, la matriz de tiras de antena y la matriz de nanodiscos [19,20,21].

Sin embargo, estos métodos de matriz sin agujeros también pueden exhibir un efecto mejorado en la foto-respuesta de los QDIP, pero su proceso de fabricación con métodos rentables y simples sigue siendo un desafío en comparación con la estructura típica de matriz de agujeros. Para las estructuras típicas de la matriz de agujeros, el tamaño de la matriz de agujeros es común en la microescala. La mejora de la foto-respuesta se produce a través del efecto plasmón en la interfaz entre el aire en los orificios de metal a microescala y el semiconductor que se encuentra debajo. El tamaño de la matriz de orificios metálicos se puede reducir aún más hasta la coincidencia a nanoescala esperada con el tamaño del punto cuántico en el QDIP a nanoescala, ya sea que los QDIP de alto rendimiento con el efecto de mejora correspondiente se puedan realizar o no. Al mismo tiempo, se necesitan más trabajos teóricos para dilucidar los mecanismos subyacentes a estos fenómenos. En este estudio, para hacer que el fenómeno sea claro, se diseñan los QDIP con las estructuras de matriz de orificios metálicos a nanoescala, y más importante en comparación con los QDIP de microescala convencionales, el efecto de mejora se explica mediante el análisis de la condición de transmisión óptica y la distribución del campo eléctrico. . Los resultados demuestran que los QDIP con las estructuras de matriz de metal a nanoescala pueden tener una absortividad de fotones de hasta el 86,47% debido a la interacción fotón-punto cuántico y el acoplamiento de luz eficiente, lo que puede abrir la puerta al diseño y la optimización del infrarrojo de tamaño nanométrico. fotodetector.

Modelo de diseño del QDIP con el Nanohole Array

En general, el QDIP consta de la región de puntos cuánticos y los electrodos, y la región de puntos cuánticos está formada por la capa de puntos cuánticos de período y las capas de barrera. En condiciones ideales (ignorando las influencias de los electrodos y el sustrato), se puede suponer que la transmisión óptica de todo el QDIP es igual a la de la región de puntos cuánticos. Por tanto, no es necesario que los electrodos y el sustrato aparezcan en el diseño del QDIP. Específicamente, la Fig.1a muestra el diseño del QDIP típico, que se compone de capas compuestas de puntos cuánticos de 5 períodos, y estas capas compuestas están constituidas por la capa de barrera A1GaAs y las capas de GaAs, incluidos los puntos cuánticos periódicos (Fig. 1b). En la configuración actual, se supone que las nanopartículas de puntos cuánticos tienen forma de cubo que está en línea con la definición de puntos cuánticos formados con muchos átomos y moléculas, y tiene 40 nm de longitud, 40 nm de ancho y 7 ~ 9 nm de altura. También se puede encontrar un modelo similar de puntos cuánticos en la literatura publicada [22]. El área del QDIP se establece en 1000 nm × 1000 nm y el grosor de las capas de barrera de AlGaAs es de 60 nm. La matriz de nanoagujeros de metal elegida como Au se coloca en las capas de nanoestructura de puntos cuánticos convencionales del QDIP convencional, que se denomina como el QDIP mejorado que se muestra en la Fig. 2. El radio de los orificios se puede ajustar en el rango de 50 ~ 70 nm . Cabe señalar que el material utilizado para formar el punto cuántico no puede considerarse simplemente como un material a granel con un cierto índice de refracción. La Figura 3 revela la característica de dispersión eléctrica del material GaAs utilizado para formar el punto cuántico utilizando el método de Edward D. Palik [23]. En la figura, la curva azul y la curva roja representan la constante dieléctrica de GaAs ε ^′ y ε ^″ , respectivamente. Las figuras 4 ayb muestran la característica de dispersión eléctrica de los GaAs, Al _0.3 Ga _0,7 Como material y material dorado, respectivamente.

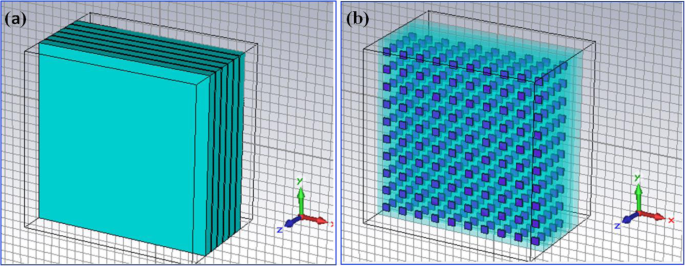
un Diagrama del modelo estructural del típico fotodetector de infrarrojos de puntos cuánticos. b Distribución de puntos cuánticos en las regiones activas con capas compuestas de puntos cuánticos de 5 períodos. Estas capas compuestas están constituidas por la capa barrera A1GaAs y las capas GaAs

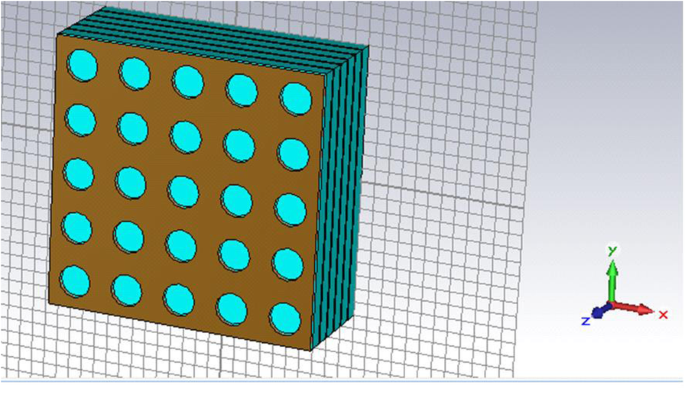
Regiones activas de puntos cuánticos con estructuras periódicas de matriz de nanoagujeros de metal para el QDIP mejorado

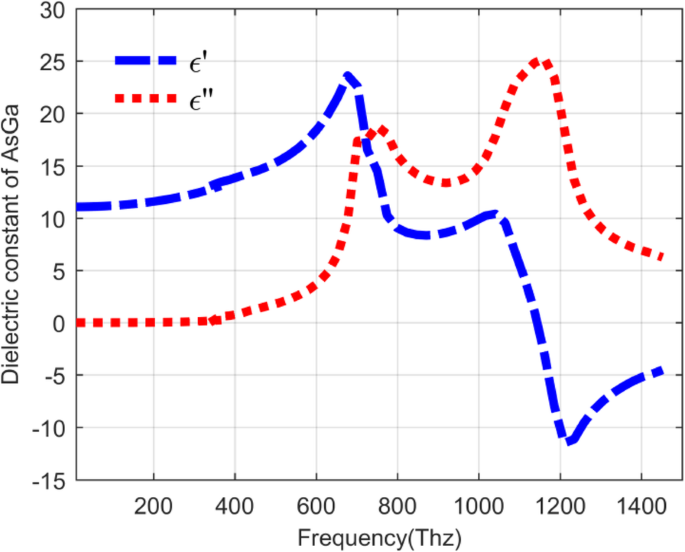
Relación de dispersión del material de GaAs

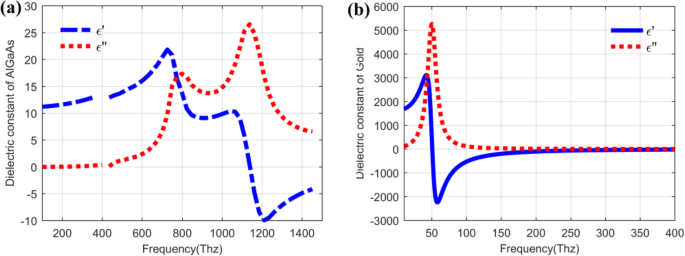
un Relación de dispersión del material AlGaAs. b Relación de dispersión del material de Au

Método de cálculo basado en la celda YEE

Basado en el modelo físico diseñado anteriormente, el método de la integración de elementos finitos se utiliza para calcular la condición de la transmisión óptica. En primer lugar, según las celdas YEE, las ecuaciones integrales de Maxwell que satisfacen el modelo anterior se escriben de la siguiente manera:

$$ {\ unción} _LE \ cdot dl =- \ frac {\ parcial} {\ parcial t} {\ int} _SB \ cdot dS $$ (1) $$ {\ unción} _LH \ cdot dl =J + \ frac {\ parcial} {\ parcial t} {\ int} _SD \ cdot dS $$ (2) $$ {\ oint} _SD \ cdot dS =q $$ (3) $$ {\ oint} _SB \ cdot dS =0 $$ (4)

En nuestro cálculo, las Ecs. 1 a 4 están discretizados. Tanto la distribución de los nodos del campo eléctrico como los nodos del campo magnético se eligen como formato de “celda Yee”. Usando la ecuación. 1 como ejemplo, el modelo electromagnético del fotodetector puede tomarse como la acumulación de “celda Yee”. Como se muestra en la Fig. 5, los cuatro lados de la celda arbitraria corresponden a la Ec. 1, que representa el vector de campo eléctrico e _i , e _j , e _k y e _l . El vector ubicado en la dirección normal es el vector de campo magnético b _n , y por lo tanto la ecuación anterior. 1 se puede reescribir como la siguiente ecuación. 5.

$$ {e} _i + {e} _j- {e} _k- {e} _l =- \ frac {db_n} {dt} $$ (5)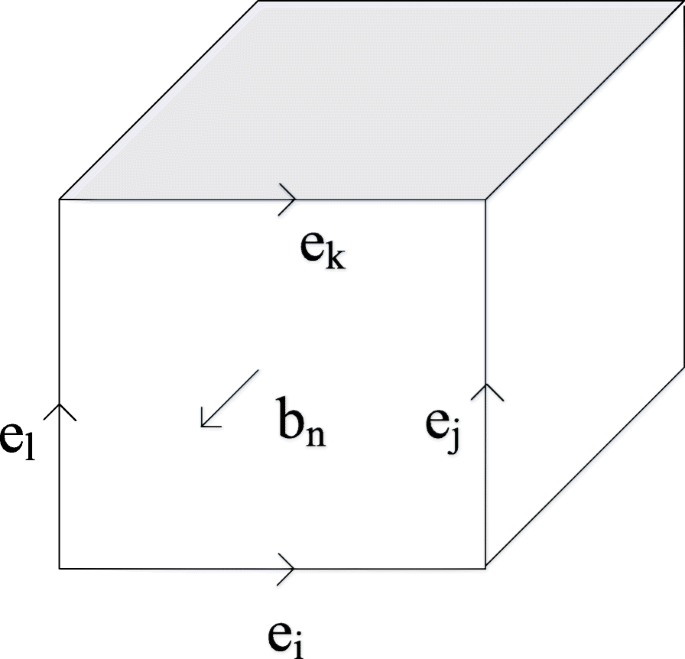

Diagrama esquemático de la "celda YEE"

Adoptando un método similar, la ecuación del modelo electromagnético de todo el fotodetector se puede escribir como:

$$ \ left [\ begin {array} {l} .. \ dots \ dots \ dots \ dots \ dots \ dots \ dots \\ {} 1 \ kern0.5em 1 \ kern0.5em -1 \ kern0.5em - 1 \\ {}. \ Puntos \ puntos \ puntos \ puntos \ puntos \ puntos \ puntos \\ {}. \ Puntos \ puntos \ puntos \ puntos \ puntos \ puntos \ puntos \ end {matriz} \ derecha] \ izquierda [ \ begin {array} {l} {e} _i \\ {} {e} _j \\ {} {e} _k \\ {} {e} _l \ end {array} \ right] =- \ frac {d } {dt} \ left [\ begin {array} {l}. \\ {} {b} _n \\ {}. \\ {}. \ end {array} \ right] $$ (6)

La ecuación 2 también se puede reescribir como:

$$ Ce =- \ overset {.} {B} $$ (7)

De acuerdo con el método similar, las otras Ecs. 2 ~ 4 se pueden discretizar como:

$$ \ overset {\ sim} {C} h =\ overset {.} {d} + j $$ (8) $$ sb =0 $$ (9) $$ \ overset {\ sim} {S} d =q $$ (10)

Combinando las ecuaciones discretizadas. 7-10 con la condición de límite, el campo eléctrico y el campo magnético pueden resolverse mediante el método iterativo. En este estudio, la estructura de matriz de orificios de metal se coloca en la parte superior del QDIP convencional y, como tal, la estructura puede facilitar el acoplamiento de luz a través de la dispersión de Bragg. Se calcula además la comunicación óptica correspondiente, que se puede discutir en la siguiente sección cuando se dan las condiciones de transmisión, reflexión y absorción. Además, basándose en la relación entre la absorción y la eficiencia cuántica, se puede dar la capacidad de respuesta del QDIP. Concretamente, es bien sabido que la responsividad del QDIP como parámetro de rendimiento muy importante se puede calcular mediante la relación entre la fotocorriente y la potencia de la luz incidente [24]. Entonces, se puede escribir como:

$$ R =\ frac {I_ {foto}} {P_o} =g \ frac {\ eta e} {hv} $$ (11)

donde yo _foto es la fotocorriente del QDIP, P es el poder de la luz incidente, g es la ganancia fotoconductora, e es la carga del electrón, h es la constante de Planck, v es la frecuencia de la luz incidente y η es la eficiencia cuántica.

La eficiencia cuántica se puede definir como la relación entre el número de huecos de electrones y el de la foto incidente, que depende en gran medida de la absorción del fotodetector. En la práctica, dado que la luz incidente ilumina directamente la región de absorción, no se puede absorber completamente debido al reflejo de la capa de contacto superior o la capa de metal [25, 26]. Por lo tanto, la eficiencia cuántica del QDIP se puede escribir como:

$$ \ eta =\ left (1-r \ right) \ left [\ exp \ left (- {\ alpha} _0d \ right) \ right] \ left [1- \ exp \ left (- {\ alpha} _0W \ right) \ right] $$ (12)

donde α ₀ W es el coeficiente de absorción del QDIP, α ₀ d es el coeficiente de absorción de la capa de contacto incidente, r es el reflejo de la capa incidente, respectivamente.

En el QDIP, la ganancia fotoconductora se puede definir como la relación entre el tiempo de recombinación de los electrones desde un estado extendido hasta un punto cuántico τ _vida al tiempo de tránsito de los electrones a través del dispositivo τ _total , y se puede mostrar como:

$$ g =\ frac {\ tau_ {vida}} {\ tau_ {total}} $$ (13)

y con la condición de que el tiempo de tránsito a través de un período de la capa compuesta de puntos cuánticos sea considerablemente menor que el tiempo de recombinación de un estado extendido a un punto cuántico [22, 27] _, la ganancia se puede escribir como:

$$ g =\ frac {\ left (K + 1 \ right) L \ mu E {\ left [1 + {\ left (\ mu E / {v} _s \ right)} ^ 2 \ right]} ^ { \ hbox {-} 1/2}} {\ mathrm {K} \ pi {a} _ {QD} ^ 2 {h} _ {QD} ^ 2 {\ sum} _ {QD} {V} _ {\ mathrm {t}}} $$ (14)

donde K es el número es la capa compuesta de puntos cuánticos, L es la distancia entre las capas de puntos cuánticos, μ la movilidad de los electrones, E es la densidad del campo eléctrico en el QDIP, v _s es la velocidad de saturación de los electrones, h _QD es la altura de los puntos cuánticos, ∑ _QD es la densidad de puntos cuánticos en cada capa de puntos cuánticos, a _QD es el tamaño lateral de los puntos cuánticos y V _t es la tasa de captura de electrones, respectivamente.

Presentada la ecuación. (12) y Ecs. (14) en la ecuación. (11), podemos obtener la capacidad de respuesta del QDIP, que se puede mostrar como:

$$ R ==\ frac {\ lambda \ left (K + 1 \ right) L \ mu E {\ left [1 + {\ left (\ mu E / {v} _s \ right)} ^ 2 \ right] } ^ {\ hbox {-} 1/2} \ left (1-r \ right) \ exp \ left (- {\ alpha} _0d \ right) \ left [1- \ exp \ left (- {\ alpha} _0W \ right) \ right]} {1.24 \ mathrm {K} \ pi {a} _ {QD} ^ 2 {h} _ {QD} ^ 2 {\ sum} _ {QD} {V} _ {\ mathrm {t}}} $$ (15)

Resultados y discusión

Según el diseño del QDIP anterior, si la luz infrarroja incidente incide en la parte superior de estos QDIP en el z -dirección del eje, los fotodetectores tendrán la reflexión y la transmisión de la luz incidente. La absortividad de los fotodetectores se puede determinar estudiando estas condiciones de transmisión óptica de la luz incidente, que pueden jugar un papel muy importante en la evaluación del rendimiento del fotodetector. La Figura 6 presenta sus condiciones de reflexión del fotodetector sin la matriz de metal (el QDIP convencional) y con la matriz de metal (el QDIP mejorado). En comparación con las dos curvas de la Fig.6, se puede encontrar que los valores del coeficiente de reflexión del QDIP convencional son ligeramente más pequeños que los del QDIP mejorado, además de los valores individuales en los rangos de frecuencia de 250 ~ 260 Thz y 279 ~ 293 Thz. . Específicamente, tomando el valor a la frecuencia de 219 Thz como ejemplo, el valor del coeficiente de reflexión del QDIP convencional es -3,91 dB, mientras que el QDIP mejorado es tan bajo como -1,31 dB. Como se ha dicho anteriormente, el QDIP mejorado puede tener un valor ligeramente más alto que el QDIP convencional, pero se puede encontrar que la absorción mínima del QDIP mejorado es bastante menor que la del QDIP convencional. Para ser específicos, la absorción mínima del QDIP mejorado es - 16,17 dB a la frecuencia de 255,10 Thz, mientras que el valor del QDIP convencional es igual a - 13,42 dB a 254,86 Thz. El bajo coeficiente de reflexión del QDIP mejorado podría atribuirse al mayor coeficiente de absorción del metal que el del semiconductor para luz infrarroja. La absorción se puede calcular basándose en las contribuciones comunes de la reflexión y la transmisión. La Figura 7a representa el coeficiente de transmisión del QDIP convencional y sus valores marcados con el color azul son claramente mayores que los del QDIP mejorado dentro del rango de frecuencia total de 200 ~ 340 Thz. Por ejemplo, a la frecuencia de 298 Thz, el coeficiente de transmisión del QDIP mejorado es solo - 10,83 dB, que es 1,60 veces más pequeño que el del QDIP convencional, que es - 4,15 dB. Según la relación competitiva entre la transmisión, la reflexión y la absorción, la disminución del coeficiente de transmisión conducirá al aumento de la absorción a condición de ignorar otras pérdidas de la luz incidente.

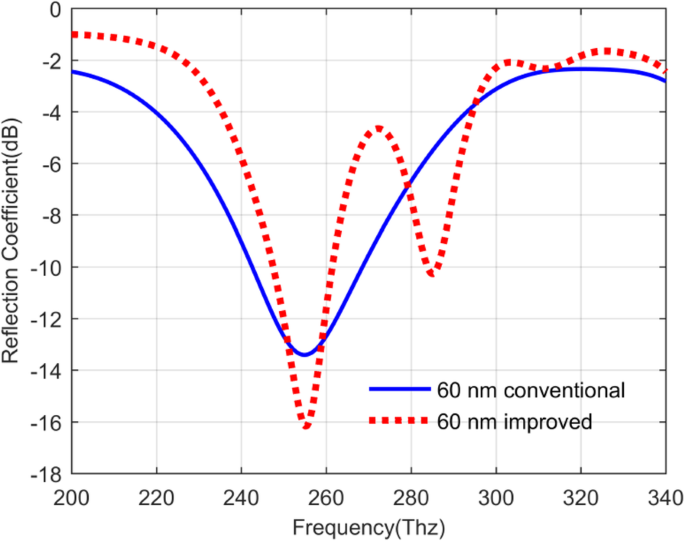
Coeficientes de reflexión del QDIP convencional sin matriz de metal (curva azul) y el QDIP mejorado con la matriz de nanoagujeros de metal (curva roja)

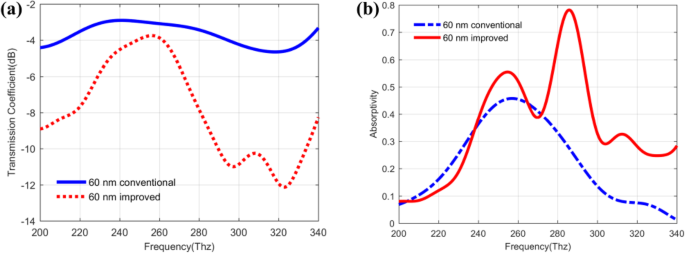
Coeficientes de transmisión ( a ) y coeficientes de absortividad ( b ) del QDIP convencional y del QDIP mejorado, respectivamente

Combinada la situación de transmisión en la Fig. 7a con la situación de reflexión en la Fig. 6, se puede calcular la absortividad del QDIP, que se muestra en la Fig. 7b. En la figura, la curva roja (marcada como 60 nm mejorada) describe la absortividad del QDIP mejorado con la estructura metálica, y la otra curva azul representa el QDIP convencional sin la estructura del agujero metálico (marcada como 60 nm convencional). Haciendo una comparación entre las dos curvas, se puede encontrar que la absortividad del QDIP mejorado es mayor que la del QDIP convencional. El máximo de la absortividad del QDIP mejorado es 0,782 a la frecuencia de 286 Thz, que es 1,71 veces mayor que el del QDIP convencional, que es sólo 0,458 a la frecuencia de 257 Thz. Las razones del aumento de la absortividad del QDIP mejorado se pueden explicar a continuación. Las estructuras metálicas de la matriz de nanoagujeros se introducen en la parte superior del QDIP convencional, y tal configuración puede favorecer el efecto de resonancia del plasmón superficial, lo que conduce al efecto de acoplamiento local de la luz incidente. Además, el efecto de acoplamiento local puede hacer que entre más luz incidente en las capas de puntos cuánticos del semiconductor que se encuentran debajo, lo que puede resultar en una alta absorción de la luz incidente y tener mejores propiedades fotoeléctricas con una mayor fotocorriente y una mayor eficiencia cuántica.

Para aclarar aún más cómo realizar el efecto de mejora del plasmón en los QDIP mejorados, también estudiamos las influencias de las diferentes estructuras de nanoagujeros de metal en la absortividad de los QDIP mejorados. Como se muestra en la Fig. 8a, las curvas de absortividad de los QDIP mejorados con diferentes radios de nanoagujeros de metal corresponden a la curva negra (50 nm), verde (55 nm), roja (60 nm) y azul (65 nm), respectivamente. Los valores de absortividad del QDIP mejorado revelan las diferentes tendencias cambiantes bajo diferentes nanoagujeros. Los valores máximos de la absortividad para el QDIP mejorado son 0,744 (curva negra a 289 Thz), 0,721 (curva verde a 291 Thz), 0,782 (curva roja a 286 Thz) y 0,707 (curva azul a 288 Thz), respectivamente. Obviamente, entre estos fotodetectores, el QDIP mejorado con un radio de agujero de 60 nm puede tener el mejor rendimiento de absortividad. Al mismo tiempo, es bien sabido que el espesor de la capa de orificios de metal también puede influir en la absortividad. Como se demuestra en la Fig.8b, cuando el espesor de la capa de metal en el QDIP mejorado se cambia de 10 a 40 nm, los valores máximos de la absortividad cambian correspondientemente de 0.667 (263 Thz para el espesor de 10 nm) a 0.782 (286 Thz para 20 nm), 0.662 (293 Thz para 30 nm) y 0.590 (262 Thz para 40 nm). Entre estos valores máximos, la capa de nanoagujeros de metal con un grosor de 20 nm puede tener el valor de absortividad más alto.

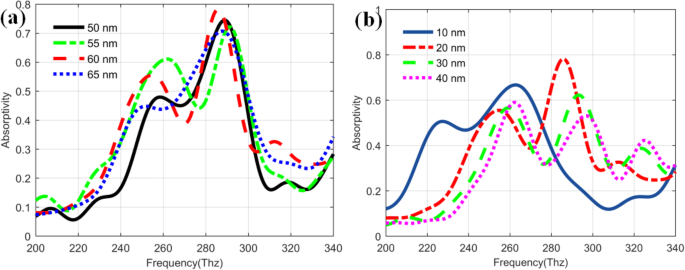
Absorción del QDIP mejorado ( a ) con diferentes radios y diferentes espesores metálicos de nanoagujeros metálicos ( b)

Para aclarar el fenómeno anterior, estudiamos más a fondo las condiciones de distribución del campo eléctrico en la superficie superior del QDIP mejorado con los diferentes radios de los orificios de metal a 286 Thz. La Figura 9 revela la distribución del campo eléctrico en diferentes radios de orificios metálicos en el rango de 50 a 65 nm. En comparación con las cuatro imágenes de la Fig. 9a, está claro que los QDIP con un radio de orificio de 50 nm (Fig. 9a) y 55 nm (Fig. 9b) pueden tener una mejora del campo eléctrico relativamente más débil debido a las distribuciones de campo eléctrico correspondientes en Fig.9 ayb que se encuentran en toda el área, incluidos los orificios y sus regiones adyacentes, y por lo tanto sus efectos de acoplamiento local del campo eléctrico pueden ignorarse, mientras que el área de acoplamiento local del campo eléctrico con un campo eléctrico alto se puede observar en la Fig. 9 c y d. Las fuertes distribuciones del campo eléctrico alrededor de los orificios en la Fig. 9c yd con la forma del anillo se pueden ubicar en la interfaz entre los orificios de metal y el aire en los orificios de metal como resultado del efecto de acoplamiento del plasmón superficial. En comparación con las distribuciones del campo eléctrico en la Fig. 9c yd, el efecto de acoplamiento del campo eléctrico en la Fig. 9c es más fuerte que el de la Fig. 9d según sus colores marcados que son una mezcla de rojo, verde y azul. En este sentido, el color rojo representa el campo más fuerte y el color azul representa el campo más débil. Según el análisis anterior, los nanoagujeros de metal con un radio de 60 nm generan el efecto de campo eléctrico de mejora por el plasmón de superficie. Para que el efecto de mejora sea más claro, la distribución del campo eléctrico en xz -plano correspondiente a la absorción máxima del QDIP optimizado a la frecuencia de 286 Thz en nuestro estudio como se muestra en la Fig. 10a, que se encuentra en la sección y =0 (correspondiente al campo de la xz -avión). En la figura, desde la dirección de z En el eje, la distribución mejorada del campo eléctrico se encuentra en la región entre los orificios de metal adyacentes que está marcada con el color rojo y el campo débil se encuentra en la región de los orificios de metal marcados con el color azul. La distribución del campo eléctrico revela directamente la absorción mejorada del QDIP. Es el efecto de acoplamiento de mejora el que conduce al aumento de la absortividad y conduce además a la alta eficiencia cuántica del QDIP mejorado. Por supuesto, también se pueden sacar las mismas conclusiones analizando la distribución del campo magnético de acuerdo con las propiedades de las propiedades electromagnéticas de la luz. Debido a que la discusión de la distribución del campo magnético es la misma que la de la distribución del campo eléctrico, no es necesario discutirla en este estudio.

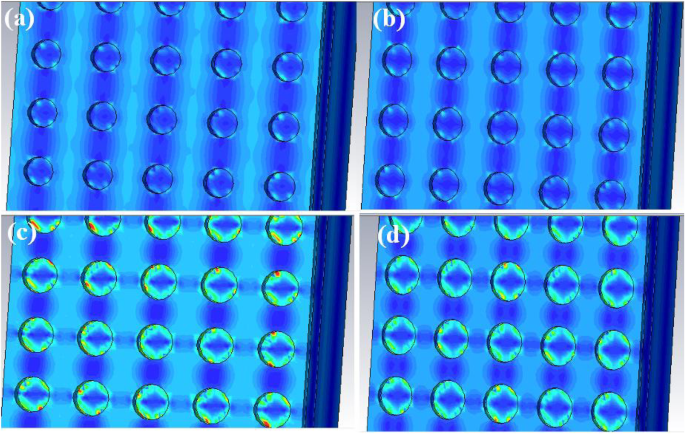
Distribución del campo eléctrico de los QDIP mejorados con diferentes radios de nanoagujeros metálicos: a r =50 millas náuticas, b r =55 nm, c r =60 nm y d r =65 millas náuticas

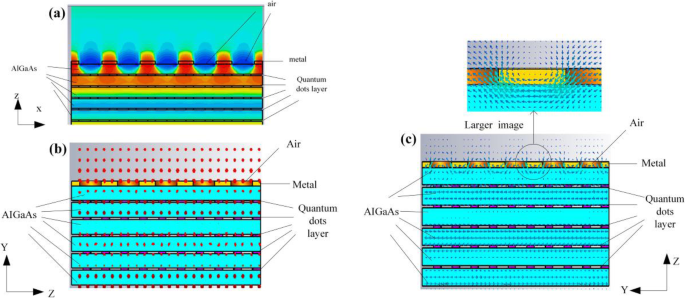
un x -dirección del campo eléctrico del QDIP optimizado. b Polarización del campo eléctrico del QDIP mejorado. c Polarización del campo magnético del QDIP mejorado

Además, como se ha dicho anteriormente, el efecto de mejora procede del plasmón superficial y se determina además el modo de la onda del plasmón superficial excitado. Las Figuras 10a yb muestran los resultados del campo eléctrico y magnético. En la figura, la Fig. 10b muestra la distribución de polarización del campo eléctrico en yz -avión. Se puede ver que el campo eléctrico es normal al yz -plano, es decir, el campo eléctrico no puede tener el E _z componente. La Figura 10c presenta la distribución de polarización del campo magnético. Se puede encontrar que el campo magnético es paralelo al yz -plano, es decir, existe la componente Hz en la dirección de propagación de la luz incidente que es z -dirección. Por lo tanto, en nuestro estudio, la onda de plasmón de superficie excitada es el modo TE. Además, para aclarar la posición utilizada para excitar el plasmón superficial, la distribución del campo magnético cerca de la interfaz del orificio metálico se muestra en la parte superior de la Fig. 10c. Se puede ver que el campo magnético en la posición entre los orificios de metal adyacentes es más fuerte que el de los orificios de metal. Además, de acuerdo con el campo eléctrico que aparece en la figura 10a, también puede probar que el campo de mejora se concentra en la ubicación entre los orificios de metal adyacentes. Por lo tanto, se puede llegar a la conclusión de que el efecto plasmón de superficie puede provenir de la superficie entre el metal y el semiconductor, que se encuentra en la posición entre los orificios de metal adyacentes. Por supuesto, vale la pena señalar que la mejora de la absorción no es solo del plasmón de superficie sino también de la reflexión mejorada de la capa de metal, lo que lleva a la absorción secundaria de la luz incidente, ya que la luz incidente se ilumina en el QDIP a lo largo de eje z.

Es bien sabido que los parámetros relacionados con las capas metálicas también pueden tener una gran influencia en el rendimiento del QDIP. Para determinar los parámetros óptimos, el grosor de la capa de barrera y la capa de puntos cuánticos se analizan y discuten en las condiciones del grosor optimizado de la capa de metal (20 nm) y el radio del orificio del metal (60 nm). La Figura 11a muestra la tendencia cambiante de la absortividad de los fotodetectores con los diferentes espesores de la capa de barrera en el rango de 70 a 85 nm. De la imagen, estas curvas de absortividad tienen una tendencia de cambio similar. Cuando los espesores de la capa de barrera varían en el rango de 70 ~ 85 nm, los valores de absortividad máxima correspondientes de los QDIP mejorados son 0.7581 (70 nm, a 322.78 Thz), 0.7763 (75 nm, a 304.84 Thz), 0.8552 (80 nm, a 292,75 Thz) y 0,8346 (85 nm, a 284,17), respectivamente. En comparación con estos valores máximos de absortividad, se puede encontrar que la capa de barrera con un espesor de 80 nm puede tener el mejor rendimiento de absortividad para los QDIP mejorados. Se corrigieron otros parámetros con los valores optimizados anteriores, las influencias de los espesores de la capa de puntos cuánticos sobre el rendimiento de absortividad para el QDIP mejorado se estudian más a fondo, y las curvas correspondientes se muestran en la Fig. 11b. A partir de la figura, se puede encontrar que la curva roja puede tener el valor de absortividad máximo de 0.8647 a la frecuencia de 295.48 Thz para el QDIP mejorado con el espesor de capa de 7 nm, lo que ilustra que el fotodetector puede tener el estado de transición óptimo.

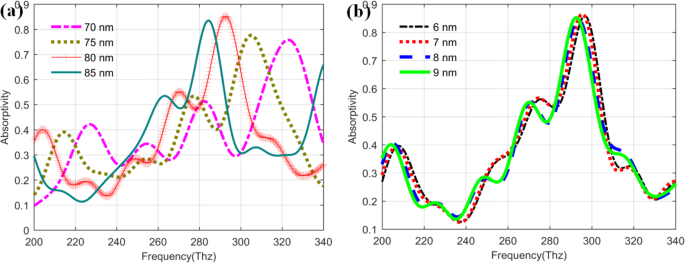
Absorción del QDIP mejorado con los diferentes espesores de a la capa de puntos cuánticos y b capa de barrera

Con base en la discusión anterior, está claro que no solo los parámetros relacionados con el QDIP pueden influir en el rendimiento del dispositivo, sino que también los espesores de la capa de puntos cuánticos y la capa de barrera también pueden determinar el rendimiento del dispositivo. En este estudio, de acuerdo con los resultados del cálculo teórico, los parámetros optimizados para los QDIP mejorados se pueden dar con el espesor de la capa de metal de 20 nm, el radio del agujero de metal de 60 nm, el espesor de la capa de puntos cuánticos de 7 nm y la capa de barrera. espesor de 80 nm. La absortividad del fotodetector óptimo puede llegar a 0,8647. Además, comparando el QDIP convencional con el QDIP optimizado como se muestra en la Fig. 12, los valores de absortividad en la curva roja son bastante más altos que en la curva azul además de los valores en el rango de frecuencia de 222.91 ~ 262.18 Thz. La absortividad máxima en la curva roja es igual a 0.8647 a la frecuencia de 295.48 Thz, que es 1.89 veces mayor que la de la curva azul (que es la misma que la curva anterior marcada como “60 nm convencional” en la Fig. 7b correspondiente a el QDIP sin matriz de orificios metálicos) a la frecuencia de 257 Thz. El cambio de frecuencia para el pico de absortividad máximo resulta principalmente del cambio en el grosor del fotodetector mejorado. Además, basándose en los parámetros optimizados de los QDIP, se calculan los espesores de la capa de puntos cuánticos y la capa de barrera, el valor de eficiencia cuántica y la capacidad de respuesta del fotodetector.

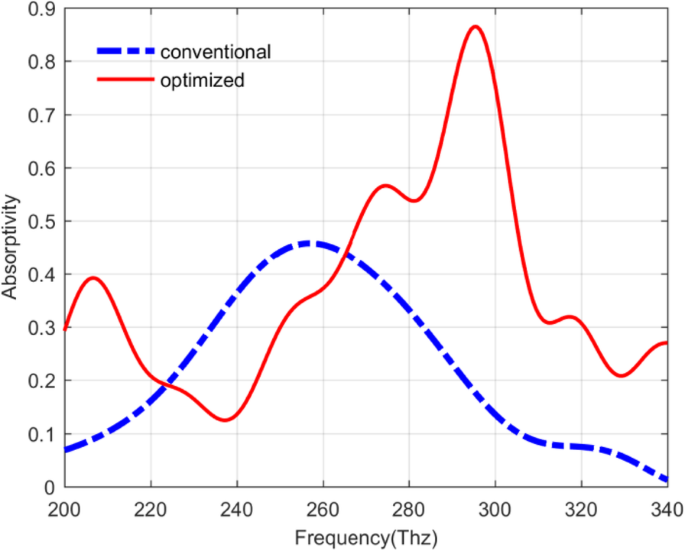
Absorptivity of the conventional QDIP in blue curve and improved QDIP in red curve with the barrier layer thickness of 80 nm

Quantum Efficiency and Responsivity of the QDIP

Based on the calculated results of the absorptivity in Fig. 12 as well as combining with the expression of the quantum efficiency and the responsivity of the QDIP above, the quantum efficiency of the QDIP and the responsivity can be calculated out, and the corresponding results are plotted in Fig. 13 a and b. Figure 13a depicts the quantum efficiency of the QDIP. In this figure, the blue dotted curve represents the quantum efficiency of the QDIP without metal array, the other red full curve is that of the optimized QDIP with metal array. Making a comparison between the two curves, it can be observed that the maximum quantum efficiency of the optimized QDIP is 0.2961 at the frequency of 295.87 Thz, and it is 1.205 times than that of the conventional QDIP, which is equal to 0.2458 at the frequency of 256.48 Thz. The increasing trend is similar to the absorptivity provided in Fig. 12 which results from the introduction of the metal hole array and the optimization of the quantum dot infrared photodetector. Based on the increasing trends for the absorptivity, we can find that the responsivity of the QDIP also reveals similar increasing trends. To be specific, Fig. 13b gives the responsivity of the optimized QDIP and the conventional QDIP, respectively. In the figure, the red curve is on behalf of the responsivity of the conventional QDIP, and the blue curve stands for that of the optimized QDIP with the metal holes layer. Similar to the analysis in Fig. 13a, the responsivity is 0.0326 mA/W at the frequency of 295.87 Thz, which is 0.0174 larger than that of the conventional QDIP at the frequency of 256.48 Thz (which is 0.0152). The increase in the responsivity can be proven in the other frequency band in the range of 229.57~254.41 Thz, which obviously demonstrates the enhancement in the performance of the photodetector due to the introduction of the metal hole array and the optimization of the quantum dot regions. Moreover, the reasons for the enhancement were detailedly discussed in detail analyzing the electric field distribution of quantum dot regions above.

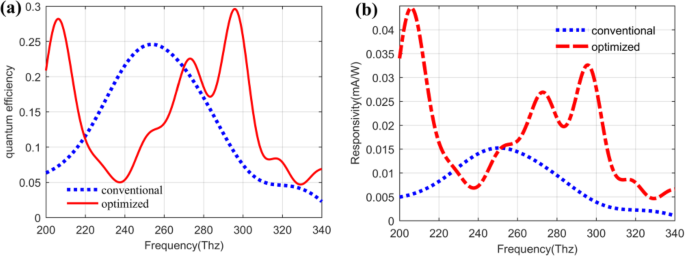
un Quantum efficiency of QDIP. b Responsivity of QDIP

Influence of the Electrodes and the Substrate

What was studied above is all under the condition of ignoring the influence of the electrodes and the substrate; in fact, the electrodes and the substrate can have certain influences on the performance, but they do not influence the description of the enhancement effects of the performance of the optimized QDIP with the metal layer. This is because the electrodes and the substrate can have almost the same influence on the absorption of the QDIP with the metal layer and without the metal layer. To illustrate the issue adequately, we recalculated the absorption of the QDIP considering the influence resulting from the substrate and the electrodes as well as the quantum efficiency, the responsivity, and so on. To be concrete, it is well known that the electrodes are generally designed at the two ends of the absorption region of the quantum dots, and thus, as shown in Fig. 14a, one is at the top of the conventional QDIP and the other is at the bottom end of the absorption region of the QDIP. That is to say, it lies at the top of the substrate, which can provide the quantum dot absorption region with the bias voltage and transmit current together with the electrodes said above. Here, it is worth mentioning that there is the metal hole array instead of the metal ring in the optimized QDIP in our study used as the electrodes. The other electrode is similar to that of conventional QDIP. Based on the above design, a concrete distribution of the electrodes is clearly calculated in Fig. 14a. Similar to Fig. 14a, in Fig. 14 b, the material of the electrodes is chosen as gold, and the substrate is chosen as AlGaAs; their thicknesses are 20 nm and 300 nm, respectively.

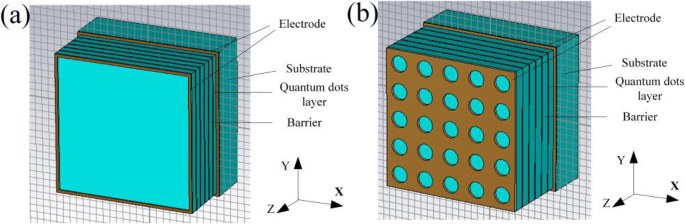
un Conventional QDIP with electrodes and substrate. b Optimized QDIP with the electrodes and substrate

Based on the introduction of electrodes and substrate in the structure of the QDIP above, we calculated the absorption of the QDIPs, and the corresponding results are compared with the QDIP without the electrodes and the substrate. Figure 15 demonstrates the influence of the electrodes and substrate on the absorptivity of the QDIP. In the figure, the blue curve and the pink curve are the absorptivity of the conventional QDIP without the electrodes and the substrate and that of the optimized QDIP without the electrodes and the substrate, respectively. The red dashed curve represents the absorptivity of the optimized QDIP with the electrodes and the substrate. Its maximum absorption is 0.7620 at the frequency of 304.35 Thz which is just 0.1027 smaller than that of the optimized QDIP without electrodes and substrate. The decrease of the absorptivity is degraded from the loss of the electrodes and the substrate, the same as the green curve with the absorptivity of the conventional QDIP with the electrodes and substrate. Compared with the absorptivity of the conventional QDIP and optimized QDIP with electrodes and substrate, the enhancement is very clear in the absorptivity of the optimized QDIP with electrodes and substrate, which is the same as the optimized QDIP in Fig. 12. In other words, though the electrodes and the substrate can result in the decrease of the absorptivity, the total absorptivity of the optimized QDIP can be enhanced compared with that of bare QDIP, and thus, the decrease can be negligible as they can have a very small influence on the description of the enhancement of the optimized QDIP when using the metal hole array.

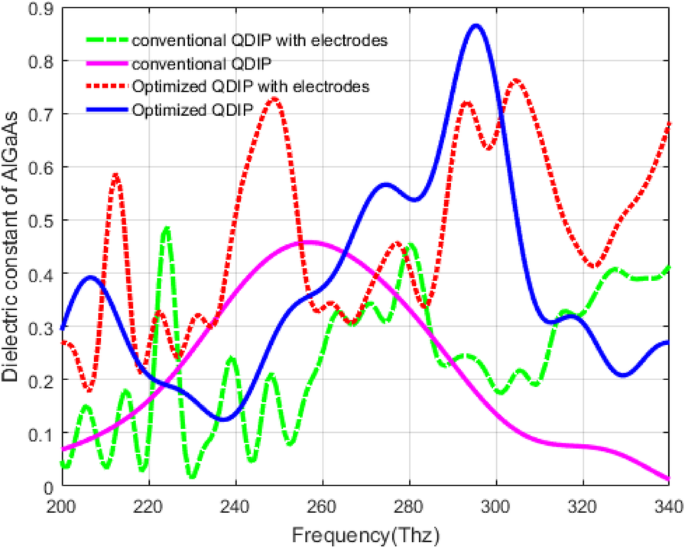
Absorption of the QDIP with electrodes and substrate

In addition, it can be observed that the change trend of the absorptivity of the QDIP with the electrodes and substrate cannot be the same as the previous curves (corresponding to the blue curve and pink curve). They are more complex with many peak values. The reasons for this phenomenon can be explained as follows. First of all, the addition of the electrodes and the substrate can produce more or less a loss and the frequency shifts due to the accumulated heating effect and the other negative influence factors. Secondly, since the material of the electrodes is chosen as the metal, in the optimized QDIP with the electrodes and the substrate, it can result in enhanced reflection and enhanced surface plasmon. The two reasons commonly favor the enhancement of the absorptivity as demonstrated in Fig. 15.

Conclusiones

In conclusion, the conventional QDIP performance can be greatly improved by adding the nanoscale metal nanohole array, and the enhanced mechanism of the performance for improved QDIPs is discussed by analyzing the reflection, the transmission, the absorption, and the distribution of the electric field. The results not only demonstrate that the improved QDIPs can have higher absorptivity than that of conventional QDIPs but also indicate that the parameters of the improved QDIPs related to the metal nanohole array together with the quantum dot composite layer can significantly influence their performance. According to theoretical calculation, the optimized parameters of the improved photodetectors are 20 nm in metal layer thickness, 60 nm in metal hole radius, 7 nm in quantum dot layer thickness, and 80 nm in barrier layer thickness. The maximum absorptivity value of the optimized photodetector can be as high as 86.47% at the frequency of ~ 300 Thz. The great enhancement of the absorptivity can be attributed to the local coupling effect caused by the enhancement of the electric field effect via the surface plasmon, and further leads to the high quantum efficiency and responsivity, which are 0.2961 and 0.0326 mA/W, respectively. It is believed that the current contribution could provide certain theoretical guidance for developing nanoscale QDIPs with high performance.