Pseudomagnetoresistencia de valle controlado eléctricamente en grafeno con distorsión de celosía Kekulé en forma de Y

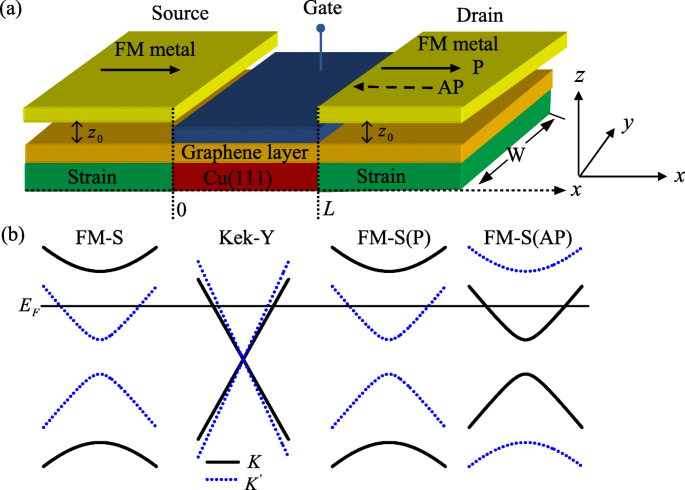
un Ilustración esquemática del VFET que utiliza un canal de grafeno con distorsión de celosía Kek-Y y un sesgo de puerta, que controla la orientación del valle de los electrones del canal. La fuente y el drenaje son el grafeno FM-S, que inyecta y detecta electrones en una polarización específica. Donde z ₀ es la distancia entre la capa de grafeno y la franja FM. L es la longitud del canal, W es el ancho de la muestra de grafeno en el y dirección y W ≫ L . b Estructura de bandas cerca de los puntos de Dirac. La línea horizontal denota la energía de Fermi (color en línea)

La propagación de cuasipartículas de excitación de baja energía en los VFET con superredes de grafeno Kek-Y se puede describir mediante los siguientes hamiltonianos de una sola partícula [10-12]

Aquí, σ y τ son las matrices de Pauli para la subred y el valle, respectivamente. P =( p _x , p _y ) es el momento de los electrones de Dirac sin masa, τ _z =± 1 para K y \ (K ^ {^ {\ prime}} \) valles, v _F =10 ⁶ m / s es la velocidad de los electrones de Dirac en el grafeno prístino, y v _τ ≃ v _F δ t / 3 t es el término de modificación de la velocidad del efecto de contracción del enlace en la red Kek-Y [12], donde t es la energía de salto entre las ciudades vecinas más cercanas para el grafeno prístino. U es la barrera potencial sintonizable en la puerta. A _M ( x ) = e v _F A _y ( x ) [19]. Los valores propios del hamiltoniano en el grafeno con distorsión de celosía Kek-Y y barrera eléctrica están dados por

Aquí, α =+ 1 (−1) especifica la banda de conducción (valencia). β =± 1 denota las dos subbandas divididas en valle de las bandas de conducción y valencia. Debido a la invariancia traslacional en y dirección, el vector de onda transversal k _y se conserva. Los estados propios en el grafeno con la distorsión de celosía homogénea Kek-Y se caracterizan por \ (\ Psi _ {\ beta} ^ {\ pm} (k_ {x \ beta}, k_ {y}) =\ frac {1} { N _ {\ beta}} \ left (1, P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm}, R _ {\ beta} ^ {\ pm} \ right) ^ {T} \), donde N _β es la constante de normalización \ (N _ {\ beta} =\ left (1 + P _ {\ beta} ^ {2} + Q _ {\ beta} ^ {2} + R _ {\ beta} ^ {2} \ right) ^ {\ frac {1} {2}} \) y \ (P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm} \) y \ (R _ {\ beta} ^ {\ pm} \) son funciones definidas de la siguiente manera:

La probabilidad de transmisión desde \ (K ^ {^ {\ prime}} \) valle a \ (K (K ^ {^ {\ prime}}) \) valle \ (T_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} \) se puede calcular utilizando la técnica de matriz de transferencia [20]. Según la fórmula de Laudauer-Btittiker, la conductancia dependiente del valle viene dada por [21]:

Aquí \ (G_ {0} =2e ^ {2} W / \ left (v_ {F} \ pi ^ {2} \ hbar ^ {2} \ right) \ left \ vert E \ right \ vert \), W es el ancho de la muestra de grafeno en el y dirección y ϕ ₀ es el ángulo de incidencia con respecto a la x dirección.

Antes de continuar con los cálculos, analizamos la estructura de la banda con k _y =0, como se muestra en la Fig. 1b. En la región de origen FM-S, la banda de energía del grafeno se escribe como \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (A_ {M} + \ tau _ {z} A_ {S}) ^ {2}} \). Uno puede encontrar que el valle degenerado es elevación y se inducen diferentes espacios en el K y \ (K ^ {^ {\ prime}} \) puntos porque el potencial vectorial total A _M + A _S actuando sobre K electrones es mayor que el potencial total del vector | A _M - A _S | actuando para \ (K ^ {^ {\ prime}} \) electrones [19]. Esto indica que solo \ (K ^ {^ {\ prime}} \) electrones pueden pasar a través de la región fuente FM-S cuando la energía incidente se encuentra en | A _M - A _S | < E < A _M + A _S [22, 23]. De manera similar, en la región de drenaje FM-S, la banda de energía del grafeno se puede escribir como \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (\ pm A_ { M} + \ tau _ {z} A_ {S}) ^ {2}} \), donde el signo ± corresponde a la configuración P y AP de las magnetizaciones. Entonces, solo \ (K ^ {^ {\ prime}} \) electrones se detectan en la estructura P y solo K los electrones se detectan en la estructura AP cuando la energía de Fermi se ubica en el rango de [| A _M - A _S |, A _M + A _S ]. En el canal de grafeno, el valle degenerado también se eleva, pero hay una diferencia importante. En contraste con el caso principal, donde las fases de K y \ (K ^ {^ {\ prime}} \) los componentes evolucionan con el mismo vector de onda [es decir, \ (k =E / \ hbar v_ {F} \)], ahora, evolucionan por separado con diferentes vectores de onda ( \ (k _ {+} =(UE) / (\ hbar v_ {F} + \ hbar v _ {\ tau}) \) y \ (k _ {-} =(UE) / (\ hbar v_ {F} - \ hbar v _ {\ tau}) \)) debido a las superredes de grafeno Kek-Y que mezclan el valle (ver Ec. 2). Esto conduce a la precesión del valle de los electrones del canal en el espacio del valle [12]. La precesión de valle en el grafeno es la base del transistor de efecto de campo de valle [8]. Y la precesión del valle también se puede caracterizar por una pseudomagnetoresistencia de valle (VPMR) en las uniones FM-S / Kek-Y / FM-S, análoga a la magnetorresistencia en las uniones de túnel cuántico basadas en grafeno con la interacción espín-órbita [4] , que se define como \ (VPMR =\ frac {G_ {P} -G_ {AP}} {G_ {P}} \), donde G _P y G _AP representan la conductancia en configuraciones P y AP, respectivamente, y \ (G_ {P} =G_ {K ^ {^ {\ prime}}, K ^ {^ {\ prime}}}, G_ {AP} =G_ {K ^ {^ {\ prime}}, K} \). La magnitud de la corriente del valle depende de la orientación magnética de la fuente y el drenaje en nuestro dispositivo considerado.

Discusiones y resultados numéricos

A continuación, presentamos los resultados numéricos para la unión FM-S / Kek-Y / FM-S en grafeno. En todo el documento, establecemos la longitud del canal L =207 nm, y restringe la energía de Fermi a 20 meV < E <140meV, se supone que satisface | A _M - A _S | < E < A _M + A _S . Las figuras 2a yb muestran los resultados calculados de la conductancia de túnel y VPMR en función de v _t con Fermi energy E =80meV y barrera de potencial rectangular U =−10meV. Podemos encontrar que G _P y G _AP tienen los mismos períodos de oscilación pero las fases inversas. Por lo tanto, el VPMR oscila con un aumento de v _t y puede aparecer el valor negativo VPMR. Estos fenómenos son similares al caso de la magnetorresistencia en uniones de túnel cuántico basadas en grafeno balístico con la interacción espín-órbita [4]. Los caracteres de oscilación de la conductancia de G _P y G _AP puede explicarse por la diferencia de fase entre los dos componentes del valle. Cuando el ángulo de incidencia ϕ ₀ =0, el cambio de fase viene dado por:\ (\ Delta \ theta =(k_ {x +} - k_ {x -}) L =- \ frac {2 (EU) v _ {\ tau}} {\ hbar (v_ {F} ^ {2} -v _ {\ tau} ^ {2})} L \). Δ θ determina la orientación de la polarización del valle antes de que el electrón ingrese al drenaje, en relación con el estado del drenaje [8]. Para Δ θ =± 2 n π , n =1,2,3 ⋯, las dos polarizaciones están alineadas, lo que conduce a la conductancia G _P máximo y VPMR un valor positivo alto (como se ve en v _τ =0,022, 0,033). Por otro lado, para Δ θ =± (2 n +1) π , n =0,1,2 ⋯, son ortogonales entre sí, lo que conduce a la conductancia G _AP mínimo y VPMR negativo (como se ve en v _τ =0.0167, 0.027, 0.038).

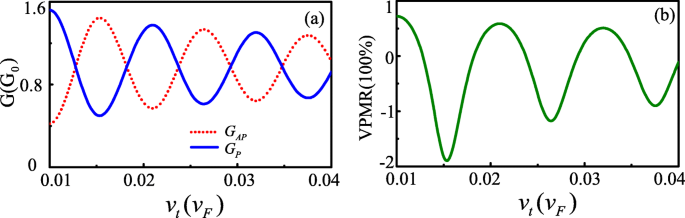
Conductancia G _{P , A P} y VPMR frente a v _t en L =207 nm, E =80meV y U =−10meV (color en línea)

La conductancia y VPMR no son solo funciones de oscilación de la modificación de la energía de salto, sino que también oscilan con la energía de Fermi y el potencial de barrera efectivo desde Δ θ Las escalas también son lineales con la energía de Fermi y la barrera potencial U . Las Figuras 3a yb muestran la conductancia en función de la energía de Fermi y el potencial de barrera efectivo, respectivamente. Los VPMR correspondientes se dan en la Fig. 3c y d. Todos muestran características de oscilación que varían con E y U valor, incluso cuando el potencial de barrera efectivo U es mayor que Fermi energy E . El origen físico de tal fenómeno está relacionado con el túnel de Klein [12]. Aunque existen fenómenos de oscilación similares de conductancia y VPMR para un aumento de E y U , también se pueden encontrar algunas diferencias. Como E aumenta, la diferencia entre G _P y G _AP la conductancia se vuelve cada vez más pequeña, lo que hace que la amplitud de oscilación de VPMR disminuya con el aumento de la energía de Fermi. Mientras esté bajo la condición Δ θ =± n π está satisfecho, la diferencia entre G _P y G _AP es mayor al aumentar U , especialmente en algún lugar, el G _P y G _AP la conductancia presenta características de conmutación. Los personajes son más deseables para la aplicación de VPMR. Sorprendentemente, el valor máximo observado de VPMR es superior al 30 000% en una E pequeña . Este valor supera con creces el MR de ~ 175 % en las uniones de tunelización cuántica basadas en grafeno balístico con la interacción espín-órbita [4] y la pseudomagnetoresistencia de ~ 100 % en grafeno bicapa controlado por puertas externas [24], que es incluso más grande que el VPMR de ~ 10000 % en un sistema de conos de Dirac fusionado [13].

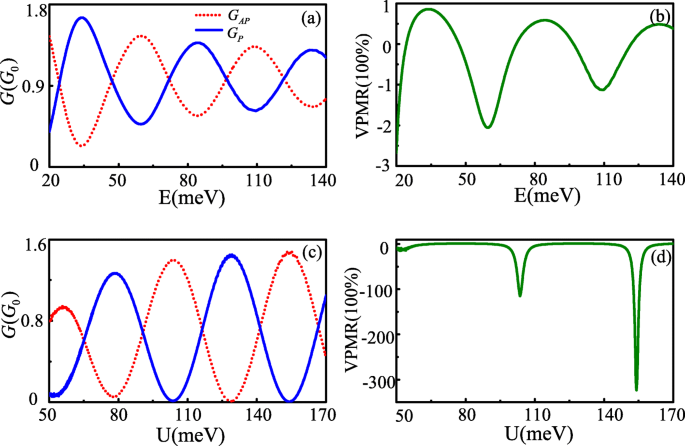
Conductancia G _{P , A P} ( a , c ) y VPMR ( b , d ) como funciones de la energía de Fermi y la barrera eléctrica en L =207 nm, v _t =0.02 v _f . los otros parámetros son U =−10meV para a y c , E =80 meV para b y d (color en línea)

Conclusiones

En conclusión, propusimos un tipo de transistores de efecto de campo de valle para electrones basados ​​en grafeno y estudiamos la pseudomagnetoresistencia de valle a través de él. Hemos demostrado que la característica de oscilación de la pseudomagnetoresistencia de valle no solo se relaciona con la modificación de la energía de salto y la energía de Fermi, sino que también se puede ajustar en gran medida mediante el potencial de barrera efectivo. La pseudomagnetoresistencia de valle sintonizada por voltaje de polarización externo beneficia al dispositivo de transistor de efecto de campo de valle, y anticipamos que los dispositivos cuánticos de valle controlados eléctricamente propuestos aquí pueden desempeñar un papel en las computadoras híbridas cuánticas y cuánticas clásicas.

La investigación adicional podría involucrar la diferente cepa (uniaxial frente a biaxial) sintonizable en la dispersión en valle de electrones y el transporte en nuestros transistores de efecto de campo de valle propuestos basados ​​en grafeno, ya que la tinción es útil para controlar el grado de dispersión en intervalos en los patrones de Kekulé [25]. . Luego, otros materiales bidimensionales (MoS ₂ , WS ₂ , WSe ₂ , etc.) análogos en grafeno también pueden proporcionar una plataforma interesante para otros transistores de efecto de campo de valle bidimensionales basados ​​en materiales con distorsión de celosía Kekulé en forma de Y.

Disponibilidad de datos y materiales

Los conjuntos de datos que respaldan las conclusiones de este artículo se incluyen dentro del artículo.

Abreviaturas

AP:

Antiparalelo

FM-S:

Deformación ferromagnética

Kek-Y:

Kekulé en forma de Y

P:

Paralelo

VFET:

Transistores de efecto de campo Valley

VPMR:

Seudomagnetoresistencia del valle

Fotodetector ultravioleta profundo de alto rendimiento basado en heterounión NiO / β-Ga2O3 Matrices de nanovarillas híbridas de CuO / TiO2 tridimensionales preparadas por electrodeposición en membranas AAO como un excelente fotocatalizador similar a Fenton para la degradación del tinte