Generación de tercer armónico plasmónico de alta eficiencia con grafeno en una rejilla difractiva de silicio en la región del infrarrojo medio

Resumen

Beneficiándose de la gran susceptibilidad no lineal de tercer orden del grafeno y la intensidad de campo significativamente mejorada de los plasmones de grafeno (GP), el grafeno ha mostrado un gran potencial para mejorar la eficiencia de conversión plasmónica de tercera generación armónica. Sin embargo, todavía carece de una configuración efectiva que pueda excitar los GP de frecuencia fundamental (FF) y guiar los GP de frecuencia de tercer armónico (THF) generados simultáneamente. Aquí, hemos propuesto una rejilla de silicio difractivo debajo de una hoja de grafeno para generar y transmitir THF GP. Los FF GP se excitan de manera eficiente al iluminar una onda plana de incidencia normal debido a la resonancia en modo guiado y luego se convierten en los THF GP con una gran eficiencia de conversión, que se origina en la intensidad de campo gigante de los FF GP. Demostramos numéricamente que, una gran eficiencia de conversión de tercera generación armónica de 3,68 × 10 ⁻⁷ se puede realizar con una pequeña densidad de potencia incidente de 0,19 MW / cm ² a 28,62 µm. Además, los THF GP generados se pueden guiar de manera eficiente a lo largo de guías de ondas GP de baja pérdida que están conectadas a ambos lados de la sección de rejilla. Nuestros resultados pueden estimular la fabricación de fuentes de luz basadas en grafeno para fotónica de silicio del infrarrojo medio y lejano.

Introducción

La generación de armónicos es un proceso óptico no lineal, en el que N fotones con la misma frecuencia ω interactuando con un material no lineal se combinan para generar nuevos fotones con frecuencia Nω . Como medio para extender las fuentes de luz coherentes a longitudes de onda cortas, la generación del tercer armónico (THG) ha atraído un enorme interés en la investigación. Convencionalmente, la generación de armónicos de alta eficiencia se realiza en cristales exóticos, pero que compromete la integración fotónica de alta densidad [1]. El silicio se ha convertido en la elección de material maduro como portador de información óptica para transmitir señales de luz en circuitos fotónicos altamente integrados. Los efectos ópticos no lineales, como la dispersión Raman estimulada [2] y THG [3, 4, 5], tienen un gran potencial para ampliar las funcionalidades de la fotónica de silicio. Sin embargo, la emisión de luz eficiente mediante el uso de silicio sigue siendo un problema debido a su banda prohibida indirecta. El uso de interacciones ópticas no lineales, como THG, parece un enfoque bastante prometedor para proporcionar luz coherente para la fotónica de silicio. En general, la eficiencia de conversión de THG (CE) para una guía de ondas óptica se puede mejorar utilizando la adaptación de fase entre el modo fundamental y el modo de tercer armónico. Este método normalmente requiere configuraciones complicadas, que suelen ser difíciles de implementar en situaciones prácticas. Se puede crear un método eficaz y robusto para mejorar el THG CE aumentando la intensidad de la luz dentro del material no lineal, lo que nos ofrece la oportunidad de relajar la exigente exigencia de la condición de coincidencia de fase. Esto se ha realizado recientemente mediante el uso de cristales fotónicos de silicio de luz lenta de factor de calidad ultra alta [3, 4, 5], microrods de sílice de pequeño volumen modal [6] y plasmones de superficie [7, 8, 9, 10]. Se ha informado que los cristales fotónicos de silicio han mejorado el THG CE a una magnitud de ~ 10 ⁻⁷ debido a la velocidad de grupo reducida de c / 40 [4]. Recientemente, se ha demostrado que los plasmones de superficie son capaces de aumentar el THG CE al orden de 10 ⁻⁵ debido a la estrecha mejora del campo eléctrico [7].

En los últimos años, la longitud de onda de funcionamiento de la fotónica de silicio se ha extendido a las regiones del infrarrojo lejano y medio (IR) debido a muchas aplicaciones potenciales, como la detección química y biológica [11]. El uso de plasmónicos en regiones de IR medio y lejano es atractivo porque la pérdida de propagación de una guía de ondas plasmónicas disminuye drásticamente a longitudes de onda más largas y también porque la sección transversal del modo de tales guías de onda es sublongitud de onda, lo que mejoraría significativamente las interacciones luz-materia como Conversión de THG [7,8,9,10, 12, 13]. Estudios recientes han demostrado que el grafeno sirve como un excelente material óptico no lineal para mejorar el efecto no lineal, lo que lleva a varias aplicaciones que incluyen cuatro ondas de mezcla [14, 15], THG [16,17,18], conmutación totalmente óptica [19], y biestabilidad óptica [20, 21], debido a su gran susceptibilidad óptica no lineal de tercer orden. Especialmente, el umbral observado de biestabilidad óptica puede reducirse en gran medida, gracias a la gran susceptibilidad óptica no lineal de tercer orden del grafeno [20, 21]. Más interesante aún, en contraste con el modo plasmón en metales, los plasmones de grafeno (GP) tienen vectores de onda significativamente más grandes, así como un confinamiento de luz mucho mayor, lo que indica la capacidad de mejorar aún más la CE de THG [13]. Sin embargo, se evita un acoplamiento directo entre los GP de frecuencia fundamental (FF) y las ondas de radiación debido a su desajuste de momento, lo que hace que la implementación de este esquema sea una cuestión difícil en la práctica. Es por esta razón que los investigadores han empleado la resonancia de modo guiado de las rejillas para abordar el problema del acoplamiento [12, 18, 20]. El esquema propuesto en la Ref. [18] está diseñado a propósito para excitar directamente los FF GP y, por lo tanto, mejorar la CE de las ondas de espacio libre de frecuencia de tercer armónico (THF) en el dominio de terahercios.

En este artículo, también hemos utilizado la resonancia de modo guiado de las rejillas para excitar de manera eficiente los FF GP en las láminas de grafeno. Diferente a la configuración en la Ref. [18] donde los GP se utilizan para mejorar la CE de las ondas de THF en el espacio libre en el dominio de terahercios, aquí, los GP se utilizan para generar THF GP en frecuencias infrarrojas en un chip de silicio. La intensidad de campo gigante de los FF GP en combinación con una gran susceptibilidad no lineal de tercer orden del grafeno da como resultado una CE notablemente mejorada de los THF GP en la hoja de grafeno en las regiones del IR medio y lejano. Observamos un estudio anterior sobre el uso de la condición de coincidencia cuasi-fase para mejorar la CE de THF GP en una superficie de grafeno [13]. Sin embargo, enfatizamos aquí, aunque se puede lograr un CE alto entre FF y THF GP en la Ref. [13], falta un acoplamiento directo entre las ondas radiativas y los GP. Por el contrario, el esquema presentado no solo puede acoplarse directamente con las ondas FF espaciales, sino que también puede generar de manera altamente eficiente los GP de THF, lo que hace que la propuesta sea adecuada para la integración en una plataforma fotónica de silicio. Además, los convertidores de frecuencia plasmónicos demostrados tienen las ventajas de compacidad y alta CE, mientras que requieren una pequeña potencia incidente [22, 23].

Métodos

La conductividad de la superficie del grafeno se puede estimar mediante la fórmula de Kubo ampliamente utilizada bajo el supuesto de potencial químico (también denominado energía de Fermi), μ _c . En las frecuencias de infrarrojos y terahercios, con | μ _c | ≫ k _B T ( k _B es la constante de Boltzmann y T es la temperatura), la conductividad superficial del grafeno podría aproximarse como

$$ {\ Displaystyle \ begin {array} {l} {\ sigma} _g =i \ frac {e ^ 2 {k} _BT} {\ pi {\ mathrm {\ hslash}} ^ 2 \ left (\ omega + i {\ tau} ^ {- 1} \ right)} \ left [\ frac {\ mu_c} {k_BT} +2 \ ln \ left (\ exp \ left (- \ frac {\ mu_c} {k_BT} \ right ) +1 \ right) \ right] \\ {} \ kern2.25em + i \ frac {e ^ 2} {4 \ pi \ mathrm {\ hslash}} \ ln \ left [\ frac {2 \ left | { \ mu} _c \ right | - \ mathrm {\ hslash} \ left (\ omega + i {\ tau} ^ {- 1} \ right)} {2 \ left | {\ mu} _c \ right | + \ mathrm {\ hslash} \ left (\ omega + i {\ tau} ^ {- 1} \ right)} \ right] \ end {array}} $$ (1)

donde e es la carga del electrón, ℏ es la constante de Planck reducida, ω es la frecuencia en radianes y τ es el tiempo de relajación del impulso que representa el mecanismo de pérdida. En nuestro estudio, se supone que la temperatura de trabajo es T =300 K. Al tomar la hoja de grafeno individual como una monocapa que no interactúa, la conductividad óptica del grafeno de pocas capas es nσ _g [24], donde n es el número de capas de grafeno ( n <6). Modelamos el grafeno como un material anisotrópico y la permitividad efectiva en el plano se puede escribir como [25, 26].

$$ {\ varepsilon} _x ={\ varepsilon} _z =1 + \ frac {in {\ sigma} _g {\ eta} _0} {k_0 {d} _g} $$ (2)

donde η ₀ (=377 Ω) es la impedancia del aire, k ₀ es el vector de onda en el aire, y d _g es el espesor total de n -capa de láminas de grafeno. La permitividad fuera del plano del grafeno, ε _y , se mantiene constante en 2,5, independientemente del nivel de Fermi [27, 28].

Resultados y discusión

Excitación de FF GP con una rejilla de silicona

En primer lugar, consideramos la excitación de los GP de FF y la generación de GP de THF en láminas de grafeno sostenidas por rejilla dieléctrica (GSSDG) como se muestra en la Fig. 1. Considerando la situación práctica de que el área de grafeno puede ser cientos de veces mayor que la sección de la rejilla, se supone que las láminas de grafeno son planas en la parte superior de las rejillas y no se ajustan a las rejillas. Hemos observado algunos estudios de investigación sobre GP apoyados por láminas de grafeno sostenidas por rejillas donde se supone que las láminas de grafeno son planas [12, 13]. Especialmente, encontramos que los resultados experimentales son muy consistentes con los resultados de la simulación, donde se supone que las láminas de grafeno son planas en el modelado [12]. Se supone que el GSSDG es infinito a lo largo de x dirección y periódica a lo largo de z dirección. Se supone que el grosor de la capa de rejilla de silicio debajo de las láminas de grafeno es de 2 μm. En este caso, la capa de rejilla se puede considerar infinitamente gruesa en el modelado, ya que el sustrato de silicio debajo de la rejilla no afecta la distribución de campo de los GP en el modelo de rejilla de aire-grafeno. La relación dispersiva de los GP admitidos por esta configuración se puede expresar como [29].

$$ \ frac {\ varepsilon_ {r1}} {\ sqrt {\ beta ^ 2 - {\ varepsilon} _ {r1} {k} _0 ^ 2}} + \ frac {\ varepsilon_ {r2}} {\ sqrt { \ beta ^ 2 - {\ varepsilon} _ {r2} {k} _0 ^ 2}} =- \ frac {in {\ sigma} _g} {{\ omega \ varepsilon} _0} $$ (3)

donde β es la constante de propagación de los GP a lo largo de z- eje, ε ₀ es la permitividad en el aire, y ε _{r 1} (=1) y ε _{r 2} son las constantes dieléctricas de los medios dieléctricos por encima y por debajo de las capas de grafeno, respectivamente. Como el período de la rejilla es mucho más pequeño que la longitud de onda de la luz en el aire, la rejilla de silicio puede modelarse aproximadamente como un medio eficaz con la permitividad equivalente [30].

$$ {\ varepsilon} _ {r2} =f {\ varepsilon} _ {\ mathrm {silicio}} + \ left (1-f \ right) {\ varepsilon} _0 $$ (4)

donde ε _silicio (=11,9) es la permitividad del silicio en las frecuencias de infrarrojos y terahercios [31], y f (= w / p ) es la proporción de llenado del silicio ( f se fija en 0.5 en este trabajo).

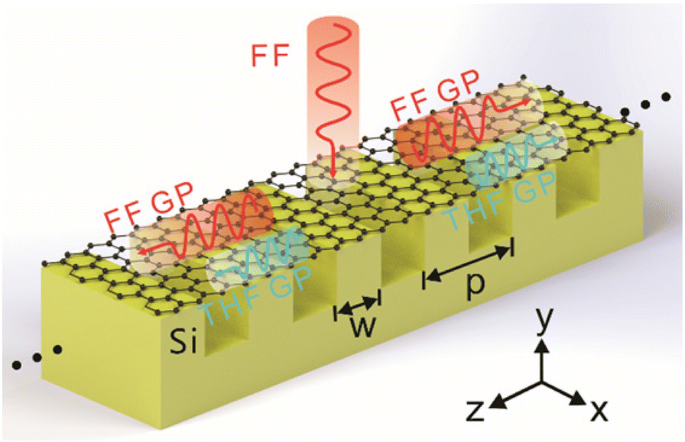
El esquema del GSSDG como convertidor de longitud de onda THG. Las FF GP (curvas rojas) se excitan con una onda plana de FF polarizada en x de incidencia normal y luego generan las THF GP (curvas azules) debido a las rejillas de silicio debajo de las láminas de grafeno. El período de la rejilla es p y w denota el ancho del silicio

La relación de dispersión de los GP en el GSSDG para diferentes parámetros ( τ , μ _c y d _g ) se muestra en la Fig. 2. En todo el trabajo, se lleva a cabo el dominio de tiempo de diferencia finita bidimensional (FDTD) con un software comercial de Lumerical FDTD Solution para realizar el modelado numérico. En la simulación de esta parte, los límites de capa coincidentes perfectos y los límites periódicos se utilizan en el y y z direcciones, respectivamente, mientras que se supone que toda la estructura es infinita a lo largo de la x dirección. Los tamaños de malla con 0,1 nm a lo largo de y dirección y 10 nm a lo largo de z dirección se utilizan para describir el grafeno, mientras que las mallas no uniformes con un valor máximo de 20 nm a lo largo de y dirección y malla uniforme de 10 nm a lo largo de z dirección se adoptan en las regiones además de las láminas de grafeno. Puede verse en las Fig.2a, d, g que, dentro del rango de longitud de onda considerado, el vector de onda de los GPs es docenas de veces mayor que el del aire, lo que indica que el campo óptico de los GPs está fuertemente confinado en el superficie de grafeno. Sin embargo, el desajuste de fase entre los GP y las ondas de radiación evita el acoplamiento directo entre ellos. La rejilla difractiva de silicio debajo de las láminas de grafeno que se muestra en la Fig. 1 puede proporcionar un impulso adicional para superar la diferencia del vector de onda para que los FF GP puedan excitarse de manera eficiente con una incidencia de onda plana. El período de rejilla, p , debe cumplir con la ecuación de coincidencia de fases como

$$ \ operatorname {Re} \ left ({\ beta} _ {\ mathrm {FF}} \ right) =j2 \ pi / p + {k} _0 \ sin \ theta $$ (5)

donde β _FF es la constante de propagación de las FF GP a lo largo de z -eje, j es el orden de difracción, y θ es el ángulo de incidencia. Para excitar los FF GP de longitud de onda efectiva de λ _FF con el orden de difracción fundamental j =1 en la condición de incidencia normal θ =0, se debe cumplir la siguiente expresión

$$ {\ lambda} _ {\ mathrm {FF}} =\ operatorname {Re} \ left ({n} _ {\ mathrm {eff}} \ right) p $$ (6)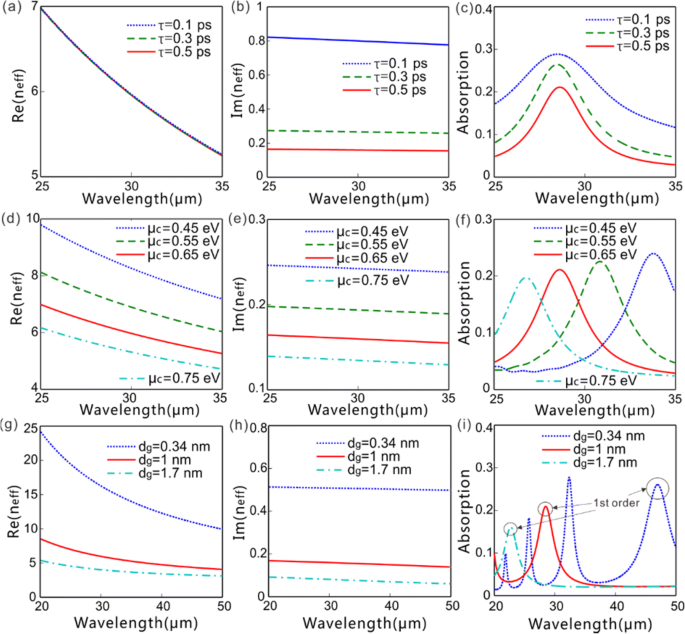

El verdadero [Re ( n _ef )] e imaginario [Im ( n _ef )] partes del índice efectivo y absorción versus longitud de onda con diferentes valores de μ _c , τ y d _g . un - c Re ( n _ef ), Soy ( n _ef ) y absorción versus longitud de onda ( τ =0.1, 0.3 y 0.5 ps, asociado con μ =0,14, 0,42, 0,69 m ² V ⁻¹ s ⁻¹ , respectivamente) con μ _c =0,65 eV y d _g =1 nm. d - f Re ( n _ef ), Soy ( n _ef ) y absorción frente a longitud de onda ( μ _c =0,45, 0,55, 0,65 y 0,75 eV) con τ =0,5 ps y d _g =1 nm. g - yo Re ( n _ef ), Soy ( n _ef ) y absorción versus longitud de onda [ d _g =0,34 nm ( n =1), 1 nm ( n =3) y 1,7 nm ( n =5)] con μ _c =0,65 eV y τ =0,5 ps. Para todos los casos, el período de rejilla se fija en p =4 micras

La Figura 2 presenta la dependencia del real [Re ( n _ef )] e imaginario [Im ( n _ef )] parte de los índices efectivos y la absorción en la longitud de onda de la luz con diferentes valores de τ , μ _c y d _g . Aparentemente, explica cómo los parámetros del grafeno influyen en los GP de FF excitados bajo la iluminación de una onda plana de FF polarizada en x de incidencia normal, donde el período de rejilla se fija en 4 μm. Tanto el verdadero [Re ( n _ef )] y partes imaginarias [Im ( n _ef )] de índices de refracción efectivos de los FF GPs disminuye con el aumento de la longitud de onda de la luz dentro del rango de longitud de onda considerado (Fig. 2a, b, d, e, g, h). Esto significa que, con una longitud de onda de luz más corta, los GP están más fuertemente confinados alrededor de las hojas de grafeno, lo que resulta en una mayor constante de propagación y una mayor pérdida de propagación. La absorción es muy sensible a la longitud de onda y aumenta bruscamente a medida que la longitud de onda incidente se acerca a la longitud de onda de resonancia (Fig. 2c, f, i). El tiempo de dispersión del portador τ determina la movilidad del portador μ en grafeno como \ (\ tau ={\ mu \ mu} _c / e {\ nu} _F ^ 2 \) con la velocidad de Fermi de ν _F =9,5 × 10 ⁴ Sra. Considerando que una movilidad del portador de μ > 10 m ² V ⁻¹ s ⁻¹ se ha logrado experimentalmente en grafeno suspendido de alta calidad [32], lo que conduce a τ > 1,5 ps, nuestra configuración de τ ≤ 0,5 ps puede reflejar la pérdida de transporte práctica de grafeno de forma conservadora. El τ , asociado con la movilidad del portador μ , influye suavemente en el Re ( n _ef ) y la longitud de onda de excitación de FF GP, pero afecta en gran medida a la Im ( n _ef ) y absorción (Fig. 2a-c). El μ mejorado _c disminuye Re ( n _ef ) y yo ( n _ef ) simultáneamente, por lo tanto, reduce la longitud de onda de resonancia de los FF GP en consecuencia (Fig. 2d-f). El Re ( n _ef ), Soy ( n _ef ), y la longitud de onda de resonancia de los FF GP se reduce con el aumento del grosor del grafeno, correspondiente al número de capas de grafeno (Fig. 2g – i).

A continuación, tomamos τ =0,5 ps, μ _c =0,65 eV y d _g =1 nm como ejemplos. La relación de dispersión de los GPs en el GSSDG se muestra en la Fig. 3a, donde las curvas de dispersión calculadas concuerdan bien con los resultados de simulación obtenidos por el software comercial Lumerical FDTD Solutions. La Figura 3b muestra la respuesta óptica de las láminas de grafeno con y sin la rejilla de silicio. Se puede ver claramente que la eficiencia de absorción (más del 20%) se mejora significativamente en λ =28,62 μm cuando la rejilla está involucrada ( p =4 μm). Por el contrario, la eficiencia de absorción se mantiene a un nivel bajo (por debajo del 2%) en todo el rango espectral considerado si no se tiene en cuenta la rejilla. La absorción notablemente mejorada para el primer caso se puede atribuir a la excitación de los GP en λ =28,62 µm. Podemos encontrar desde el | E | distribuciones en λ =28,62 μm (Fig. 3c) que el GP excitado es el modo de resonancia de onda guiada fundamental ( j =1). Se puede ver en la Fig. 3d que la longitud de onda resonante del modo fundamental con respecto al período de rejilla de las simulaciones numéricas concuerda bien con el resultado teórico predicho por la Ec. (6).

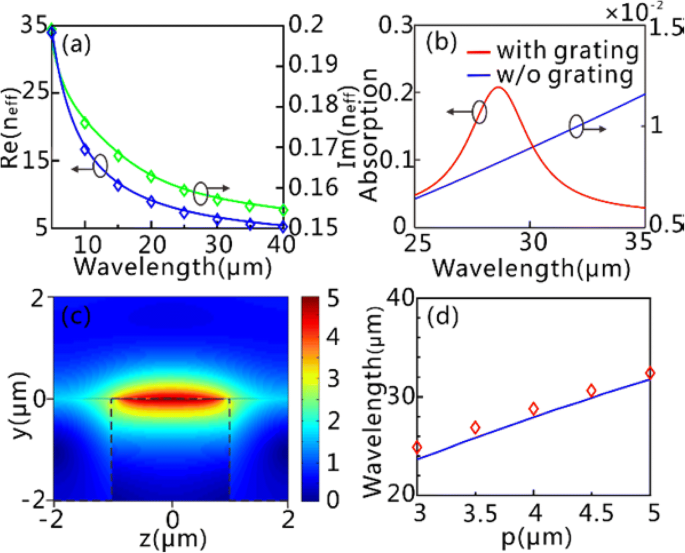
FF GP y mejora de campo en el GSSDG. un Curvas de dispersión de los GP en el GSSDG. Las líneas sólidas azul y verde corresponden a la [Re ( n _ef )] e imaginario [Im ( n _ef )] parte del índice efectivo recuperado de Eq. (3), respectivamente, mientras que los rombos azul y verde se obtienen a partir de simulaciones numéricas. b Espectros de absorción con sustrato de rejilla (línea roja) y sustrato de silicio puro sin rejilla (línea azul). c El normalizado | E | distribuciones del modo GP fundamental a 28,62 μm. Las líneas punteadas negras delinean la capa de silicio. d La longitud de onda de excitación del modo GP fundamental frente al período de rejilla. La línea azul se recupera de la ecuación. (6) y los rombos rojos son de simulación numérica. En b y c , P se establece en 4 μm. Todos los resultados de la simulación son recuperados por el software comercial Lumerical FDTD Solutions

Cabe señalar que se produce un campo plasmónico muy mejorado en la superficie del grafeno debido a la reducción significativa de la velocidad de grupo de los FF GP (decenas de veces menor que la velocidad de la luz en el aire). El campo plasmónico experimenta una mejora del campo eléctrico 5 veces más alto que las ondas planas iluminadoras, lo que es muy probable que genere THF GP con una CE significativamente mejorada, en combinación con la gran no linealidad óptica de tercer orden del grafeno [16, 17]. La respuesta no lineal del grafeno puede describirse mediante el coeficiente de conductividad no lineal definido como [17].

$$ {\ sigma} _3 \ left (\ omega \ right) =i \ frac {3 {e} ^ 2 {\ left ({ev} _F ^ 2 \ right)} ^ 2} {32 \ pi {\ mathrm {\ hslash}} ^ 2 {\ mu} _c {\ omega} ^ 3} $$ (7)

donde la velocidad de Fermi ν _F =9,5 × 10 ⁴ m / s.

Generación de THF GPs

Luego comparamos la intensidad del campo eléctrico de los THF GP en la superficie del grafeno cuando las láminas de grafeno se sostienen con y sin rejilla. Las condiciones de contorno en las simulaciones FDTD son las mismas que las utilizadas en las Figs. 2 y 3. La intensidad del campo eléctrico normalizado (NEFI) en función de la longitud de onda se presenta en la Fig. 4a, cuando las láminas de grafeno se iluminan con luz de onda continua de incidencia normal (CW) con una densidad de potencia de 0,11 MW / cm ² y la longitud de onda central de 28,62 µm. Aquí, el NEFI se obtiene normalizando la intensidad del campo eléctrico a su valor de 28,62 μm (FF) con la estructura de rejilla. Se puede observar que se produce un pico aparente en THF en el espectro NEFI con estructura de rejilla (GSSDG), en comparación con el espectro NEFI sin rejilla involucrada. Definiendo la CE como \ ({\ int} _0 ^ p {P} _y ^ {THF} dz / \ left ({P} ^ {FF} p \ right) \), donde \ ({P} _y ^ {THF } \) es el y componente del vector poynting en THF, y P ^FF es la densidad de potencia de la luz incidente, el CE alcanza hasta 5,71 × 10 ⁻⁷ para el GSSDG. Se puede inferir fácilmente que la excitación de los FF GP contribuye a la mejora de la CE de los THF GP. Las distribuciones de campo de la parte real de E _y en THF que se muestra en la Fig. 4b validar la generación de GP de THF en la superficie del grafeno.

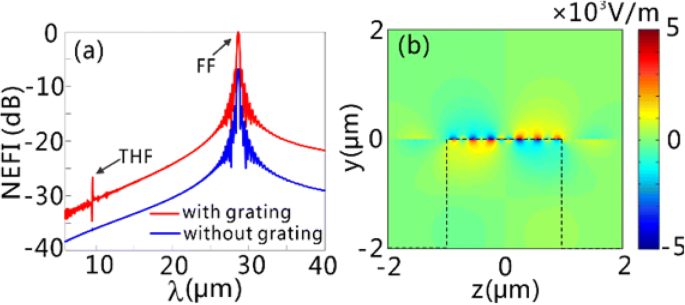
Generación de THF GPs en el GSSDG. un El NEFI para la estructura con (línea roja) y sin (línea azul) rejilla normalmente iluminada por luz CW con la densidad de potencia de 0,11 MW / cm ² y la longitud de onda central de 28,62 µm. Los dos picos en la línea roja denotan los GP de FF ( λ =28,62 μm) y los GP de THF generados ( λ =9,54 μm), respectivamente. b La distribución de la parte real de E _y para los GP de THF generados. La línea discontinua negra en b representa los contornos de la capa de silicio. Los parámetros estructurales de GSSDG son los mismos que los de la Fig. 3

El GSSDG como fuente de luz para fotónica de silicio de infrarrojo medio

A continuación, consideramos el uso del convertidor de longitud de onda plasmónica GSSDG para proporcionar directamente una fuente de luz para los circuitos fotónicos integrados de silicio. Como ejemplo que se muestra en la Fig. 5a, dos guías de ondas de plasmón de silicio-grafeno (GSPW) están unidas al GSSDG en ambos lados. Los GSPW se eligen de modo que sean capaces de guiar a los GP a través de una amplia banda espectral que cubre los GP de FF y THF. Dado que las distribuciones de campo modal de los modos FF y THF GP en el GSSDG (asimétrico respecto a la superficie del grafeno) presentan una fuerte similitud con los modos GP admitidos en el GSPW, se puede deducir que, una vez que la sección de rejilla se ilumina con incidencia normal Las ondas FF, las GP de FF y THF generadas por encima de la región de rejilla se pueden acoplar eficazmente a las GSPW en ambos lados. Realizamos simulaciones FDTD para validar nuestra predicción. Los límites de la capa coincidente perfecta se utilizan tanto en y y z direcciones en el modelado. Simulamos una onda de luz FF de incidencia normal que incide en la sección de rejilla y mostramos las distribuciones del campo eléctrico para los GP de FF y THF (Fig. 5b, c). Se utiliza una fuente de luz de campo total / campo disperso para garantizar que solo la sección de rejilla se ilumine con luz incidente en la simulación [33]. Se utilizó un límite de absorción perfectamente emparejado para absorber totalmente todas las ondas de luz que alcanzan el límite de la región de cálculo. La Figura 5b muestra que los FF GP se excitan en la superficie de grafeno sobre la rejilla y luego se propagan a lo largo de los GSPW en ambos lados. En la Fig. 5c, podemos encontrar además la apariencia de los THF GP en la superficie del grafeno, tanto en la sección de rejilla como en los GSPW. Aquí, la CE se define como

$$ \ mathrm {CE} =\ int {P} _z ^ {T \ mathrm {HF}} \ mathrm {dz} / \ left ({P} ^ {\ mathrm {FF}} {N} _pp \ right) $$ (8)

donde \ ({P} _z ^ {\ mathrm {THF}} \) es la z -componente del vector poynting en THF, \ (\ int {P} _z ^ {\ mathrm {THF}} \ mathrm {dz} \) es la densidad de potencia de salida de THF GP en GSPW, P ^FF es la densidad de potencia de las ondas de luz FF incidentes, y N _p es el número de período de rejilla. Se puede ver en la Fig. 5d que el CE de THG alcanza el valor máximo de 3.68 × 10 ⁻⁷ (- 64,3 dB) en el límite de la red y se atenúa exponencialmente a lo largo de la dirección de propagación debido a la pérdida de absorción óhmica del grafeno.

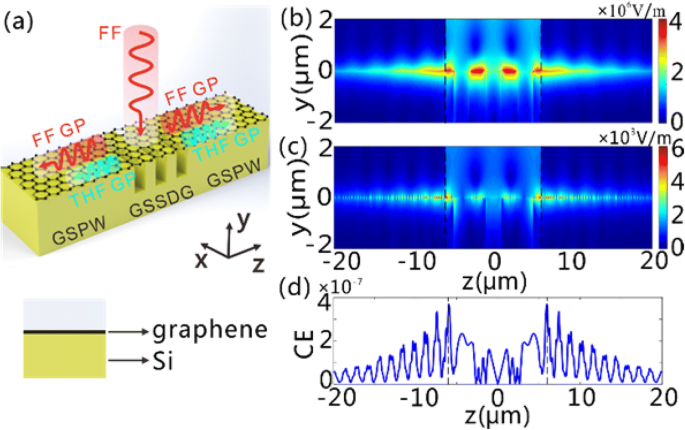
Generación de GP FF y THF en el GSSDG y los GSPW conectados. un Los esquemas del GSSDG y los GSPW conectados en ambos lados cuando una onda plana de incidencia normal con polarización X de FF ilumina la estructura. Los GP de THF se generan y guían a lo largo de los dos GSPW después de que los GP de FF se exciten en el GSSDG. La sección transversal del GSPW se presenta en el panel a continuación, en el que se indican las hojas de grafeno y la capa de Si. b , c El | E | distribuciones de b FF y c THF GPs en el y - z plano, ya que la sección de rejilla está iluminada por luz CW con una densidad de potencia de 0,19 MW / cm ² a 28,62 µm. d El CE de THG a lo largo de la z dirección. Las líneas punteadas negras en b - d representan las interfaces entre GSSDG y GSPW. En b - d , N _p se fija en tres

Es importante discutir los factores que afectan el THG CE, que es clave para evaluar el rendimiento del dispositivo de un convertidor de longitud de onda THG. Para un proceso THG, siempre se espera lograr el mayor CE con una potencia de bomba relativamente pequeña. Estudios anteriores demostraron que, al aumentar la intensidad del campo local en los materiales no lineales de tercer orden, se obtiene una mejora notable de la CE de THG con una potencia de bombeo significativamente reducida [3, 4, 7]. La Figura 6a muestra la influencia de la densidad de potencia de las ondas de luz incidente en la CE máxima en las GSPW, que aumenta con la densidad de potencia. Tenga en cuenta que el CE máximo alcanza hasta 3,68 × 10 ⁻⁷ incluso si la densidad de potencia de las ondas de luz incidente es tan baja como 0,19 MW / cm ² , que es 6-7 órdenes de magnitud más pequeños que aquellos dentro de la misma banda espectral [22, 23]. Mostramos en la Fig. 6b que el número usado de período de rejilla, N _p , también afecta a la CE en las GSPW. Cuando N _p aumenta, una porción reductora de los THF GP generados en el centro de la rejilla llega a los GSPW debido a la mayor pérdida de propagación inducida por la absorción de grafeno. Sin embargo, la potencia de entrada, asociada con N _p , presenta realce lineal. Por lo tanto, la CE máxima de los THF GP disminuye con el aumento de N _p . Enfatizamos aquí que la densidad de potencia de salida absoluta de los THF GP debería ser más significativa para guiar el diseño de un convertidor de longitud de onda de THG para aplicaciones prácticas, una vez que se fija la densidad de potencia incidente. Aunque la CE máxima de los THF GP se encuentra en N _p =2 en nuestro caso, la densidad de potencia de salida de THG se aproxima al máximo cuando N _p ≥ 3 (figura 6b). Por tanto, hemos empleado 3 periodos de rejilla para la demostración de la generación de THF GPs en las GSPW. Para la implementación experimental futura con el diseño actual, el área de la fuente de entrada FF excede la región de la red y se mantiene constante cuando se genera THF GP con diferentes números de red. En este caso, la CE debe escribirse como

$$ \ mathrm {CE} =\ int {P} _z ^ {\ mathrm {THF}} \ mathrm {dz} / \ left ({P} ^ {\ mathrm {FF}} S \ right) $$ (9 )

donde el área de la fuente de FF, S , es constante. Por lo tanto, la densidad de potencia de salida será proporcional al CE y, por lo tanto, se debe seleccionar correctamente el número de rejilla óptimo para maximizar la densidad de potencia de salida de THF GP.

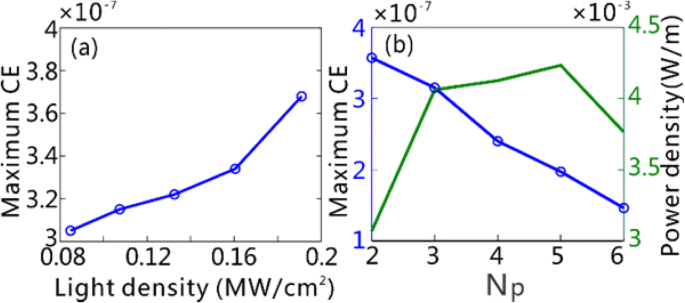
un El CE máximo de THG en función de la densidad de potencia incidente para N _p =3. b El CE máximo y la densidad de potencia de salida máxima de THG en función del número de períodos de rejilla N _p utilizado, respectivamente. La densidad de potencia incidente se fija en 0,11 MW / cm ²

Las características físicas del grafeno también pueden afectar el rendimiento del dispositivo de THF GP una vez que la estructura estudiada que se muestra en la Fig. 5a esté lista. La energía de Fermi, μ _c , y el número de capas de grafeno cambiará significativamente la longitud de onda de resonancia de los FF GP (Fig. 2f, i) y, por lo tanto, afectará también a la longitud de onda de generación de los THF GP. En contraste, el τ , asociado con la movilidad del portador μ , apenas influye en la longitud de onda de resonancia de los FF GP, así como en la longitud de onda de generación de los THF GP (Fig. 2c). Sin embargo, la pérdida de propagación de FF GP y THF GP puede reducirse mediante el uso de un τ mucho más grande. (Fig. 2b), lo que aumenta así notablemente la CE de THF GP. Considerando que una movilidad del portador de μ > 10 m ² V ⁻¹ s ⁻¹ ( τ > 1,5 ps) en el experimento [32], nuestros resultados de simulación ( τ =0.5 ps) que se muestra en (Figs. 3, 4, 5 y 6) puede presentar de manera conservadora el rendimiento del dispositivo del generador THF GP en la Fig. 5a.

Finalmente, vale la pena discutir las influencias de la rugosidad de la superficie de las láminas de grafeno en el rendimiento del dispositivo. La rugosidad de la superficie del grafeno podría potencialmente dispersar el plasmón y, por tanto, la pérdida de plasmón aumentará [34]. El generador de THF GP propuesto que se muestra en la Fig. 5 puede fabricarse basándose en la tecnología de fabricación micro / nano actual. Primero se puede girar un polimetacrilato de metilo (PMMA) de 270 nm de espesor sobre el sustrato de silicio. La capa de PMMA se desarrolla con MIKE \ IPA después de un proceso posterior de litografía por haz de electrones. Después de eso, se deposita una capa de Cr de 60 nm de espesor sobre la capa protectora con el método de deposición por evaporación por haz de electrones. El sustrato de rejilla de silicio se puede formar con técnicas de grabado, tales como una máquina de plasma acoplada inductivamente. Seguido por el método de grabado en húmedo, la capa de Cr residual se elimina mediante el método de grabado en húmedo. Por último, las láminas de grafeno se transfieren a la rejilla de silicio para formar la estructura final que se muestra en la Fig. 5.

Conclusión

Hemos demostrado numéricamente la generación de THF GP en una hoja de grafeno sobre rejillas de silicio con las ondas planas de incidencia normal en las regiones del IR medio y lejano. Se demostró que los THF GP se generan y transmiten en la superficie del grafeno, y la CE se mejora drásticamente debido a la intensidad de campo significativamente mayor de los FF GP excitados en combinación con la gran susceptibilidad no lineal de tercer orden del grafeno. Los THF GP generados se pueden acoplar convenientemente a un GSPW, lo que facilita enormemente la integración del convertidor de longitud de onda basado en grafeno en una plataforma de silicio. Nuestra propuesta puede estimular la fabricación de fuentes de luz basadas en grafeno para fotónica de infrarrojo medio y lejano en una plataforma de silicio y, por lo tanto, ampliar las funcionalidades de la fotónica de silicio, como el procesamiento de señales, la espectroscopia y la detección.

Abreviaturas

CE:: Conversion efficiency
CW:: Onda continua
FDTD:: Finite difference time domain
FF:: Fundamental frequency
GP:: Graphene plasmon
GSPW:: Graphene-silicon plasmon waveguide
GSSDG:: Graphene sheets sustained by dielectric grating
PMMA:: Polimetacrilato de metilo
THF:: Third-harmonic frequency
THG:: Third-harmonic generation

Información sobre la absorción celular y el tráfico intracelular de nanopartículas Estudio comparativo sobre la estabilidad microestructural de níquel nanocristalino electrodepositado previamente recocido durante el laminado en paquete

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias